EARLY ENERGETICS
THE HISTORIAN OF SCIENCE approaches nineteenth-century physics in a gingerly spirit. He has before him a great story, perhaps the greatest in his subject. But he is sure neither how to tell it, nor that he always has it right. At what point, he asks himself uneasily, is he beginning to write popular science in retrospect? Compared to conventional fields of historiography, the history of science is but sparsely underpinned by a professional literature of special studies. And here in nineteenth-century physics what is elsewhere a paucity thins to a near vacuum. The historian has to write directly from the sources, and to seek such guidance as he may find from scientists themselves, attributing this or that importance to their predecessors. His situation is like that of a diplomatic historian who should have nothing to work with beyond texts of treaties and official documents, to be studied in awareness of the acts and sayings of practicing diplomatists of his own time. One must respect such men of action, and also recognize that their lights are usually not historical. But an additional and even more serious obstacle lies across the history of science.
Ordinary language always fails in some degree to convey the findings of science. In physics, the measure of this inadequacy curves sharply upward between Carnot and Helmholtz, or between Faraday and Maxwell. After the middle of the century, it mounts exponentially toward the catastrophe of communication which everywhere besets modern learning. Einstein remarks somewhere that as the concepts of science are simplified and become ever more beautiful, the mathematics expressing them grows correspondingly more esoteric. Only the mathematical physicist can follow the lengthening chain of abstraction which connects concepts to human experience, and only he can appreciate the beauty of the simplicity. The rest of us are reduced to silence—to silence and to admiration, but less of physics than of Einstein. Modern physics, indeed, is so many things besides ideas about nature. It is abstraction. It is technique. It is instrumentation, housed in machines complex and expensive beyond the dreams of the most grandiose old engineer. It is power. It is education, diplomacy, and war. Materially at least, it holds all things for all men, the hope or the end of the world. And it is far from clear what degree of entry the history of ideas will give into all this. Techniques crowd out ideas nowadays. They change faster. They have come to have more history—in the last half-century far more. Nevertheless, even though the conscious or assumed structure of ideas about nature occupies a diminishing sector in the expansion of science, it remains a thread. Perhaps it must still be taken as the guiding thread, unless science is to abandon intellectuality altogether for technology at one end or mathematicization at the other, those extremes touching where operationalism meets symbolic logic in the new nominalism.
This is not to apologize, but simply to warn the reader that what follows is rather more provisional than what has gone before. It is a stab in the light. For nineteenth-century physics is to be treated as an end and a beginning. The great themes of classical physics culminated. The great physicists thought of themselves as pressing Newtonian physics into all corners of the structure of nature. Only a few philosophers fretted about the foundations. No one expected the second, the twentieth-century revolution in physics. Nevertheless, that revolution goes far back into the failure of classical physics quite to fit the shape of things. It is impossible to write its history except in the consciousness of that revolution pending, just as no man may write the history of the ancien régime except in the knowledge of the French Revolution.
It will be well to recall, therefore, the bold strokes in the world picture of classical physics. So far had Cartesian rationality prevailed over Newtonian caution during the Enlightenment, that the physical universe had come to seem a problem in mechanics. An idealized solar system served as gross model for a world of inertial billiard balls moving and impacting through an infinite void. The eighteenth century brought great triumphs. Lagrange completed the formal development which made analytical mechanics a purely rational subject, abstracted from all particular physical properties of bodies or graphic representations of their motions. In less elegant vein, Laplace demonstrated as instances of mutual gravitation among planets the apparent anomalies of observational astronomy. Benjamin Franklin brought electrostatics within the ambit of conservation laws. Coulomb demonstrated the inverse square relationship in the interaction of electrostatic charges. This was the most dramatic encouragement to belief in the formal universality of Newtonian force law. And surely the faith was worthy that other phenomena would come in, once techniques of measurement were sufficiently refined: the emission and motion of light corpuscles; the bonds between chemical atoms and molecules; the flow and interchange of energies in electricity, magnetism, and heat, following some fluid model of an imponderable hydraulics.
How facile it is to identify in retrospect the two flaws in this structure, the one metaphysical and turning on the Newtonian doctrine of space, the other physical in the excessive commitment to corpuscular mechanism. It will be remembered with what sang-froid Newton had incorporated the void of the atomists into the structure of classical physics. The void is what makes inertial motion conceivable, and its introduction is the device by which Newton accommodated the discontinuity of matter to the continuous extension of space. But Newton’s void is Epicurean only in function. In form it is Euclidean, not only an arena but a coordinate system for motions of which the equations are written in analytical geometry. Now, the essential point of classical, Galilean kinematics had been to turn motion from metaphysical change into a relational state. Bodies are in motion, not in expression of indwelling essence, but in relation to other bodies. Into this kinematics, Newton inserted his distinction between relative and absolute motion, and made the void of space the reference against which absolute motion occurs.
It was a stroke of brilliant nonsense. As Leibniz very properly objected, the constitutive role of the void posits the existence of the nothing. Rather than define space as a substance consisting of emptiness, Leibniz preferred to consider it as itself a relation, that of simultaneous events. These objections were covered up in the contumely which classical science heaped upon all metaphysics, and were buried under the gathering mass of Newtonian successes. But they were buried alive. For it was to turn out, as often before in the history of thought, that metaphysics has a way of avenging itself. Meanwhile, Newton filled space with aether, weightless, elastic, vibratory, to serve as medium for transmission of gravitational force. But aether aroused no great interest throughout the eighteenth century. Unlike space, it remained a word rather than a working part of physics. It came forward into prominence only in the nineteenth century, as an increasingly important compensation to the inadequacies of a mechanics consisting only in forces defined by the motion and impact of particulate bodies.
These inadequacies began to emerge in phenomena before they did in philosophy. And the movement of nineteenth-century physics may be followed in the continuing dialogue between unity in nature and variety in events, the structure of the whole or the behavior and arrangement of the parts. Any physical science must concern itself with the interaction of matter and energy and with the properties of space—among them, the propagation of physical phenomena. And these alternative and complementary preoccupations may be seen as polarizing respectively the two great aspects of nineteenth-century physics—thermodynamics and mechanics. Both evolved in similar patterns: exorcising by a sophisticated statement a hypostatic fluid constructed for spatial transmission. Both illustrate the dictum that one trouble emerging in classical physics was that its concepts were too complex and its mathematics too elementary. The study of forces inherited such a fluid from Lavoisier. This was caloric, the matter of heat, which had extension, served conservation (supposedly), and was (therefore) mathematicizable. Its effect on particles of matter was taken to be repulsive. Caloric vanished into a more elaborate energetics, of course. Nevertheless, as a construct it was the starting point of thermodynamics. The problems of that science did not easily reduce to kinetics. Was it to be a parallel branch of physics, therefore, or perhaps even an alternative to classical corpuscular mechanics as the route to a unified science? There were those at the end of the century who still thought so, and whose hopes were to prove not so much wrong as irrelevant to the way the world is made.
For in the event, mechanics, the other great branch of physics, proved the more fruitful in its revolution into electromagnetic theory. There aether played the role opposite to caloric. It was a medium for attractive rather than repulsive forces, but it was the same kind of construct, not comparable to the life-forces of vitalism or the sympathies of Goethe, but a mathematicizable notion under conservation. Aether accommodated more fundamental relations than caloric, and was correspondingly more difficult to exorcise; but as caloric disappeared into thermodynamics, so aether did into relativity, the culminating expression of the effort to express the unity of law in a geometric continuum. In the nineteenth century, field phenomena—everything for which the aether was invoked, especially the wave theory of light and electromagnetic induction—represented thinking about spatial problems. And here it is obvious what the opposing terms were: kinetics, statistical mechanics, ultimately radioactivity and the discontinuities which argued quanta.
IN 1824 A YOUNG FRENCH ENGINEER, Sadi Carnot, published a short memoir, Reflections on the Motive Power of Heat. It begins as a piece of reasoning about steam engines, and this no doubt was what inspired L. J. Henderson’s famous remark that science owes more to the steam engine than does the steam engine to science. Outwardly, Carnot’s spirit seems Baconian enough. He sees the implications for all civilization of the permanent revolution in power. “Already the steam-engine works our mines, impels our ships, excavates our ports and our rivers, forges iron, fashions wood, grinds grain, spins and weaves our cloths, transports the heaviest burdens, etc. It appears that it must some day serve as a universal motor, and be substituted for animal power, waterfalls, and air currents.” Consider England’s industrial leadership: “To take away today from England her steam-engines would be to take away at the same time her coal and iron. It would be to dry up all her sources of wealth, to ruin all on which her prosperity depends, in short, to annihilate that colossal power. The destruction of her navy, which she considers her strongest defense, would perhaps be less fatal.” But Carnot was no Watt, and no Brunei. He was the son of Lazare Carnot, the Revolutionary organizer of victory, himself an engineering mathematician. Too, indeed almost inevitably, he was a graduate of Ecole Polytechnique. In his rationalism and technocracy he was one of the purest spirits to emerge from that portentous institution, at once Cartesian and positivist, which would assimilate all engineering to science, and all statecraft to social science, the engineering of humanity. For the steam engine only provided Carnot with problems, and the empirical flavor is soon lost in the thought experiment: “Notwithstanding the work of all kinds done by steam-engines, notwithstanding the satisfactory condition to which they have brought today, their theory is very little understood, and the attempts to improve them are still directed almost by chance.”
The question as it first presents itself is an old one—whether there is any limit in the nature of things to the “motive power” that can be drawn from heat, and whether any other agent might be found to transmit that power more effectively than steam. Polytechnique trained its men to put things in the most general way possible, however, and Carnot immediately abstracted the problem of “the production of motion by heat” from the particular characteristics of steam engines, to the hypothetical properties of “all imaginable heat engines.” On this universal basis, the subject becomes something quite other than the magic touch of British enterprise. It becomes a question of the adequacy of a mechanistic physics for the description of nature. So long as engineers had to do only with power that could be levered, pullied, geared, or screwed out of the motions of men or animals, wind or water, the theorems of classical mechanics sufficed. “All cases are foreseen, all imaginable movements are referred to these general principles, firmly established and applicable under all circumstances. This is the character of a complete theory.” But as soon as heat became the motor, classical mechanics failed to help. The concept of moment did not connect the thrust of steam against the piston to the fall of temperature within the cylinder. And to arrive at a theory which would help, the laws of physics would need to be “extended enough, generalized enough, to make known beforehand all the effects of heat acting in a determined manner on any body.”
Carnot wrote in quiet language. But his proposition was very radical, and must really be allowed to redress any picture which would represent nineteenth-century physics as sunk in naïve mechanism until put straight (or crooked) by Einstein. Carnot did not discuss the inadequacy of mechanism. Rather, he resumed that theoretical study of heat as a physical problem which had been seriously inaugurated by Laplace and Lavoisier. Lavoisier, it will be remembered, had conceived of caloric as a physical agent, a vehicle of expansive force, accompanying chemical transformations but not participating in them. Fourier published his perfected Analytical Theory of Heat in 1822. That memoir created the mathematical techniques for describing the conduction of heat in solids and in liquids, but excluded from analytical consideration the “repulsive forces produced by heat” which determine the behavior of gases. Like Lagrange’s Analytical Mechanics, which was its inspiration, Fourier’s was a work of differential equations rather than of physics. It enabled the analyst to calculate the flow of heat, but denied to the imagination any model of wherein heat consisted, any consideration of what might be done with it, or any notion of how its study might lead further into nature. Carnot may have felt the physical sterility of this. He would study power. But he would be no less general—he would abstract from any particular type of engine, but not from the capacity of heat to move bodies. In Carnot’s thought, heat is the sensible effect of caloric. And caloric is not intrinsic to steam or the hot body in general, but rather is associated with it, as it is in Lavoisier’s concept of chemical reaction.
Since energetics became the opposite pole to mechanics in nineteenth-century physics, it will be best to be explicit about what was to be at stake. Newtonian mechanics knows only the extension, mass, and motion of bodies acted on by the (mathematical) force of gravity. It defines force in terms of those quantities, as the product of mass times change-of-motion. (In the concept of mass lurked another metaphysical difficulty, comparable to that which vitiated the absoluteness of space, but that is not for the moment germane.) Extension, mass, and velocity—even amidst the Newtonian enthusiasm of the eighteenth century, such measurements seemed hardly adequate to embrace all the action in the world. What was the physicist to make of manifestations of action? Of Power? Work? Heat? Fire? Chemical Activity? Magnetism? Electricity? Life? Before Newton, force itself had been just such a vague word. It continued to be used ambiguously through half the nineteenth century. And one task of physics would be to divest some such words of all physical meaning, and to invest the others with positive significance.
The need had been obscurely felt from the beginning. It was a difficult issue between the Cartesians and Leibniz whether momentum or vis viva (mv or mv2) be the quantity conserved in a dynamical situation. The former corresponds to the Newtonian definition of force as mass times acceleration. That question had been resolved analytically rather than physically by Lagrange, after having been dismissed by d’Alembert as semantic, though at the expense of what was to become the concept of work. Finally, of course, when the status of heat as a form of energy was established, the problems would collapse into a single subject. But historically, it was heat rather than vis viva (kinetic energy) which brought them before the bar of physics.
In a sense, physics itself was on trial. Were these problems to extend and sophisticate mechanics? Or was physics to enrich itself in them and transcend mechanics? Ultimately, the mechanists, notably Maxwell, Boltzmann, and Gibbs, would make thermodynamics into kinetics, a special case of a statistical mechanics. But it is the enrichers who were always the more verbal and eloquent, and who would treat the phenomena of thermodynamics as manifestations of a deeper level of organization than any to be attained by bodies in motion. And their appeal is always just a touch suspect, in that one senses in it, perhaps, some lingering yearning to transcend a dismalness in science, to replenish the old Democritan death of the soul in things.
This, however, is to go way beyond the implications of the Carnot memoir. Carnot did not labor the inapplicability of the theory of machines to heat. Like the early students of electricity, he simply accepted it, and adopted the hydraulic analogy of heat as caloric, a fluid under conservation. For caloric was not some fuel of motion. A conservative quantity is not consumed. Motion in the steam engine is to be attributed to the flow of caloric, “its transportation from a warm body to a cold body, that is, to its re-establishment of equilibrium—an equilibrium considered as destroyed by any cause whatever, by chemical action, such as combustion, or by any other.” And it is hardly possible to insist too strongly upon the originality and clarity of this observation: that the marshalling of heat creates a deliberate disturbance in the state of things, and that it is the return to evenness, caloric seeking its own level, from which power may be drawn.
Rather than looking forward to entropy, however, Carnot was certainly looking backward to hydrodynamics, and particularly to a treatise, General Principles of Equilibrium and Motion, which his father had published in 1803. Brunold has pointed out the similarity of the language. Thus the father on water power:
To employ a wheel of which the blades are moved by impact of the water is not the way to produce the greatest possible effect in a hydraulic machine turned by running water. In practice, two factors prevent this means from realizing the greatest effect. First, it is essential to avoid any percussion whatever. Secondly, the fluid after impact would still have a velocity, which would appear as a pure loss, since this residual velocity could then be employed to produce a further effect, augmenting the initial impulse. In order to make a perfect hydraulic machine, therefore, the core of the problem would consist in (1) arranging that the fluid should lose all its motion in its action on the machine, or at least that it should retain only the quantity necessary to get clear of the mechanism; (2) that it should lose all this motion by insensible degrees, without any percussion occurring, either in the fluid, or in the interactions of the solid parts of the machine. Further than this, it would make very little difference what the form of the machine was; for a hydraulic machine which fulfills these two conditions, will always produce the greatest effect possible.
And thus the son on caloric power:
Since every restoration of equilibrium in caloric may cause the production of motive power, any restoration of equilibrium which takes place without production of that power ought to be considered as a pure loss. Further than this, a moment’s thought will show that any change of temperature which is not due to a change in the volume of bodies must be just such a useless restoration of equilibrium in caloric. The necessary condition for maximum effectiveness, then, is that in bodies used to realize the motive power of heat, no change of temperature should occur which is not due to a change of volume. Reciprocally, whenever that condition is fulfilled, the maximum will be reached.
This principle ought never to be overlooked in the construction of heat engines. It is their fundamental basis. If it cannot be rigorously observed, at least the departures should be as slight as possible.
For this reason alone, it is hopeless to think of using solid or liquid bodies as heat engines. This is a purely theoretical assertion, quite independent of the practical difficulty of devising linkages to harness the expansion and contraction of solids and liquids. It has to do only with the impossibility of getting much motion out of the cooling of a hot bar of metal or whatever, for liquids and solids are cooled not by expansion, but by conduction or radiation. It is an important finding but not surprising (after all, neither Watt nor anyone had ever tried to substitute a thermocouple for a boiler). The same is true of Carnot’s other proofs; that the capacity of a heat engine is a function of the absolute temperature differential, that the difference (but not the ratio) of specific heats at constant pressure and constant volume is the same for all gases. In each case, the reasoning rather than the application is what holds the interest.
The reasoning founded the science of thermodynamics. Carnot asks us only to remember what we know from experimental physics of the thermal behavior of gases. Compression heats gases and expansion cools them. Let us suppose that we wish to maintain unchanged the temperature of a gas under compression. We must somehow carry off the caloric. Reciprocally, we must supply caloric to keep the temperature unchanged during an expansion. This in no way implies, however, that the caloric in question pertains to volume as opposed to pressure, which alters inversely in service to Boyle’s law. And this is all we know. We do not know what laws relate changes in caloric to changes in volume, or whether its quantity varies with the identity of the gas, or its density or temperature. These relations are what we must establish, and for that Carnot shows us that, in fact, we already have all we need to know.
We are to imagine an idealized system, exhibiting the elements of any heat engine. The body A represents the furnace. It is an inexhaustible reservoir of caloric. The body B represents a condenser, or sink for caloric, and stays unchangeably at a lower temperature than A. A quantity of any gas (say air) is confined initially in the cylinder under a weightless, frictionless piston. Arrangements are possible to let caloric flow without leakage from A to the cylinder to B.
A sequence of imaginary operations ensues in six steps: (1) Caloric flows from A to the cylinder. (2) The piston rises from cd to ef, all the while that A supplies caloric to keep the temperature constant. (3) Caloric from A is cut off, but the piston moves on out (with the gas cooling now) to gh, where the temperature has fallen to that of B. (4) Now the gas is compressed and the piston returns to cd, but the caloric displaced is permitted to flow into B so that the temperature continues constant at the lower level. (5) The flow of caloric to B is cut, and the compression continues to bring the temperature back to A with the piston at ik. (6) The cylinder and A are again connected, and the constant temperature expansion transpires to ef. And from here on, the operations may be repeated as often as desired.
Thus did the idea of reversibility spring full cycle from the mind of its creator. Carnot immediately pointed out that these events could equally well be imagined backwards.
The result of these first operations has been the production of a certain quantity of motive power and the removal of caloric from the body A to the body B. The result of the inverse operation is the consumption of the motive power produced, and the return of caloric from the body B to the body A; so that these two series of operations annul each other, after a fashion, one neutralizing the other.
And it is obvious that the diagram (first imagined by Clapeyron in 1834) by which modern texts render the ideal cycle is simply a more economic representation: the isothermal followed by the adiabatic expansion, the system restored to the initial condition by an isothermal followed by an adiabatic compression, the work delivered (or expended) denoted by the area enclosed in the graph.
Nevertheless, Carnot’s argument does not quite lead to the conclusion expected by the modern student. It is we, the readers, who have to perceive the proportionality of the segment cdki to the area of the pressure-volume graph as a measure of the work performed. Carnot did not define the concept of work. He could not, so long as he held that no caloric was lost. His interests were otherwise directed. In step (6) he returned his piston past cd to ef, the point of maximum volume at initial temperature. For he wished to reason (quite correctly) that for any given position of the piston, the temperature is higher during expansion than during compression.
During the former the elastic force of the air is found to be greater, and consequently the quantity of motive power produced by the movements of dilation is more considerable than that consumed to produce the movements of compression. Thus we should obtain an excess of motive power—an excess which we could employ for any purpose whatever. The air, then, has served as a heat-engine; we have, in fact, employed it in the most advantageous manner possible, for no useless re-establishment of equilibrium has been effected in the caloric.
That is to say, all the caloric which has flowed from A to B has been employed in the motions given to the piston. None has been wasted in friction, dissipated by conduction, or employed to change the state of the air in any but a volumetric respect. And even in this ideal arrangement, than which none could be more advantageous, caloric still has to flow from a body at higher temperature to one at lower to produce motion. Nor is there any way to get more power out of the system. If there were, it would be possible to use some of the excess to direct caloric from B back to A, to pump it uphill so to say, “from the refrigerator to the furnace.” If this were possible, one could restore the initial conditions without expenditure of caloric (that is to say the position of the piston at terminal point of the cycle would be cd instead of ik, and the motive power requisite to compress it to ik would be disposable).
This would be not only perpetual motion, but an unlimited creation of motive power without consumption either of caloric or of any other agent whatever. Such a creation is entirely contrary to ideas now accepted, to the laws of mechanics and of sound physics. It is inadmissible.
Statements of the second law of thermodynamics sometimes take a form which imply that the impossibility of creating energy, which is to say perpetual motion, were a finding of thermodynamics. Historically at least, this is quite misleading. Historically speaking, the science rather rests upon Carnot’s accepting that impossibility. This is more fundamental an assumption than that caloric may be treated under conservation. It is simply an axiom about method on which the very possibility of science was conditional. And its justification was nothing less than the whole experience of “sound physics.”
Carnot’s is no cautious memoir, therefore. He never wrote the formula,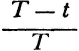 
, for the motive power of heat. Nevertheless, his argument does establish that that power depends only on an absolute temperature differential, and not on what vapor fills the heat engine. But even while Carnot proved the indifference of the results to the identity of the gas, he also showed that the expansibility of vapor is the most efficient means of realizing the motive power of heat. He tabulated the specific heats of different gases at constant volume and constant pressure to bring out the invariance of the difference. And only a really daring mind would study the properties of this or that fluid—steam, oxygen, air, or whatever—in order to rise above them, and to found its conclusions rather on the conservation of a hypothetical fluid, which those actual fluids only convey, and ultimately on the impossibility of perpetual motion. For Carnot’s was a fertile imagination. He conceived the very categories of thermodynamic reasoning. The ideal heat engine, the isothermal and adiabatic changes, the reversible cycle—these are to thermodynamics what force, velocity, mass, and linear extension have been to mechanics.
It remained to name and to mathematicize them, and especially the notion of reversibility. For therein lies the most intimate dependence of thermodynamics on its historical antecedents in caloric. In the evolving structure of thermodynamic theory, the reversible process may be compared to the concept of inertial motion in seventeenth-century mechanics. No real motion can persist forever in a straight line. No real process is reversible. Nevertheless, it is the ideal datum which gives the hand of mathematics something abstract to lay hold on. Inertial motion, it will be recalled, had entered science as a physical consequence of Descartes’ geometrization of space-matter, combined with the immutability of God. Carnot, too, introduced the notion of reversibility as a physical expression of the continuum, of flux as flux was understood in the infinitesimal calculus. Important results depended upon altering the conditions of the imaginary experiment so that the temperatures of A and B should differ indefinitely little. Then we might neglect steps (3) and (5), since these (adiabatic) changes of volume would not sensibly affect the cycle. We would be left with an isothermal expansion and compression. Now, by the gas laws of Mariotte (Boyle’s law to an Anglo-Saxon), Gay-Lussac, and Dalton, the pressure-volume relations are invariant for all gases at constant temperature. It follows as a simple consequence that the quantity of caloric involved in an isothermal change is independent of the identity of the gas. Similarly (not to follow the reasoning in detail), the demonstration of the constant difference of specific heats turns on neglecting an infinitesimal term.
For Carnot thought about the fluidity of caloric as one might imagine a materialization of the calculus. The analysis did not require a physicist to follow some actual reversibility to and fro. Rather, its cogency depended on the physicist’s being interested only in the initial and the final states of the system. Instead of an actual steam engine, full of friction, leaking heat at every pore, one in which the piston could scarcely tell whether the slam of the steam was adiabatic or isothermal, Carnot would meditate about an ideal engine, departing from and returning to the same initial state. And just so might the physicist always substitute for a real, irreversible change, a theoretical, reversible change—as long as the initial and final states were comparable. And since a reversible change is one in which each state differs infinitesimally from that preceding it, reversibility as a fiction implies continuity and permits the application of the differential calculus. That was the work of Clapeyron, who published a mathematicization of Carnot’s theory in the Journal de l’École Polytechnique for 1834. So completely had Carnot’s work been lost to view a quarter of a century later, that Clausius knew it only through the medium of Clapeyron’s treatment. Reversibility was the essential condition from which Clausius drew the concept of entropy. It is, he wrote, like “a limit which may never be reached, but which may be approached as closely as we wish. In theoretical considerations, therefore, we may speak of the limiting case as if it were realizable, and even as a limit it plays an important role in theory.”
Anticipating Clausius will suggest the debt which the science of thermodynamics owes to the caloric theory of heat exchange as fluid flow. For the complementary view of heat as motion in the particles of matter imposed a kinetic model of gases, to be analyzed by statistical techniques which did not yet lie readily to hand. Carnot’s results are often said to be independent of his use of caloric. It may be so. He himself qualified his belief in caloric in later jottings, found only after his early death. Certainly one may everywhere substitute the phrase “quantity of heat” for caloric in his memoir without spoiling the reasoning. Even so may one deprive Newton of his aether without spoiling anything about his physics except its intelligibility. But there is another question, more interesting historically. Without the model of caloric, would Carnot ever have arrived at those results? What would he have thought about? Conservation of what? The impossibility of perpetual motion in what? For it is difficult to see how a kinetic theory of heat could have led anyone to the essential and paradoxical notion of reversibility. Lacking a supple statistics, what could reversibility have meant—in a box of giddy molecules? With no sense of direction? In any case, the notion of heat as motion did not lead to reversibility, either in Rumford, who went beyond Lavoisier’s calorimetry to found the experimental physics of heat, or in Joule, who determined its mechanical equivalent.
CARNOT’S MEMOIR remained unappreciated and almost unknown until the 1840’s, the crucial decade for the foundations of thermodynamics. Otherwise, it might seem as if these problems had been straightened out backwards. For it is the second law of thermodynamics, not the first, which treats of direction and uses the analytical concept of reversibility abstracted from the caloric theory of heat-flow. The first law, on the other hand, the law of the conservation of energy, derived historically from the complementary criticism of the notion of heat as substance, and depended on demonstrations of the convertibility of heat into “motive power.” Nor is convertibility at all the same thing as reversibility. For Carnot was wrong about the conservation of heat. It does not just flow. In actual conversions, heat is degraded. What is conserved is energy, a more general quantity, which is not to be measured as a substance, but changes in which are to be expressed as a function. Where thermodynamics obtains, this function is the sum of work and heat, and heat appears as one form of energy.
Historically, the first law of thermodynamics emerged as one of the rewards rendered physical of vague notions of the interchangeability, perhaps the identity, of ultimate forces of nature, possibilities which tantalized the imagination of the early nineteenth-century physicists. Thus, light entails radiant heat, and heat-soaked iron glows first red, then white. Chemical and electrical forces passed one into another through Volta’s pile, and in its successor, Humphry Davy’s wet cell. Heat disappeared into or boiled out from chemical reactions. The electric current appeared as heat in wires. In 1820 Oersted detected its magnetic effect. Electricity might even have to do with life forces, since it had first betrayed itself in the twitching of Galvani’s frog leg. The first experiments (expressly designed) to demonstrate the convertibility of motion through friction into heat were by Benjamin Thompson, a Yankee country boy turned Tory and careerist, who served the King of Bavaria as ordnance expert, was created Count Rumford, and married (unhappily) Lavoisier’s widow. He argued that heat consists in motion by reaming a cannon barrel with a blunted borer and flamboyantly boiling water with the heat produced. That was in 1798. Rumford was too early to know other convertibilities. Nor did he quantify that of motion into heat. Forty years later these wider possibilities were the starting point for the man who did, a student of John Dalton, James Prescott Joule of Manchester.
Joule was a no-nonsense physicist, very dexterous and very nice in his experimental conscience. His father, a brewer, set him up snugly in a private laboratory. He married at the age of thirty-nine, chose Chamonix for his wedding trip, and took with him a long thermometer to try the Alpine waterfalls at various altitudes, in the hope of finding the temperature increasing with the motion. The trip held disappointment. There was too much spray. Nor was his belief in some common origin of the forces of nature less matter of fact. Early experiments suggested a constant ratio between the expenditure of mechanical power and the evolution of heat. “I shall lose no time in repeating and extending these experiments,” he wrote in 1843, “being satisfied that the grand agents of nature are by the Creator’s fiat indestructible; and that, wherever mechanical force is expended, an exact equivalent of heat is always obtained.” And he got on with the job of measuring it, with no further ado about theology or metaphysics. He wrote a summary paper in 1849. It is prefaced by two statements, the first from Locke:
Heat is a very brisk agitation of the insensible parts of the object, which produces in us that sensation from which we denominate the object hot; so what in our sensation is heat, in the object is nothing but motion.
And the second from Leibniz:
The force of a moving body is proportional to the square of its velocity, or to the height to which it would rise against gravity.
Joule was a man of few and simple ideas. He spent the years between 1843 and 1849 demonstrating that the first of these statements is reducible to the second.
Electromagnetism had dominated the physics of the 1830’s, and it was through inconclusive experiments on motors that Joule came to the study of heat. He despaired of putting electricity on a footing to compete economically with steam. In 1843 the British Association for the Advancement of Science met in Cork. Joule read a paper “On the Calorific Effects of Magneto-Electricity.” He had made a little electromagnet spin in a field under water. Joule measured the current induced, the heat generated, and the energy expended. Each of the last two quantities proved proportional to the square of the current, and was, therefore, equivalent one to the other. By those first determinations 838 foot-pounds corresponded to the amount of heat required to raise one pound of water through one degree Fahrenheit. Then he sought an independent (and direct) confirmation of the same quantity. He set up fluid friction by passing a perforated piston to and fro in a cylinder of water, and found 770 foot-pounds for the mechanical equivalent of the heat produced. At so preliminary a stage, and with such small temperature differences, agreement on the order of magnitude outweighed the discrepancy in the figures, and Joule devised techniques capable of vindicating his views on convertibility with precision.
In the meanwhile, Carnot’s work came to Joule’s attention, and he put in hand experiments of his own on temperature changes in gases undergoing compression or expansion. He expressed his findings as a dissent from the “opinion of many philosophers” that the mechanical power of the steam engine arises simply from the passage of heat from a hot to a cold body. Joule attributed to Carnot and Clapeyron an opinion which Carnot at least had never held, that the vis viva of flowing caloric was the source of power. He dismissed this reasoning “because it leads to the conclusion that vis viva may be destroyed.” Any theory which “demands the annihilation of force, is necessarily erroneous.” Thus by a logic which (like Carnot’s) excludes the inadmissible, Joule requires the reader to accept his own hypothesis. On expansion in the cylinder, the steam loses heat exactly in proportion to the mechanical force communicated to the piston. No vis viva is destroyed, because instead of consisting in the flow of heat as substance, it is conserved in the total situation which transfers vis viva from the particles of steam to the outward thrust of the piston, and cools the steam in equivalent degree.
It remained to determine that equivalence directly, and Joule imagined and designed a famous piece of apparatus. He had a small brass paddle-wheel made which turned horizontally in a calorimetric bath. It was set in motion like a pendulum clock by the descent of weights. Thus the work done by the weights descending directly measured the heat consumed in raising the temperature of the water by the friction of the blades. Joule appreciated the importance of reducing turbulence. His vessel contained a system of vanes for baffling the rotation of the liquid. In later determinations he substituted sperm oil and mercury for water. The paper which summarized the series in 1849 states his results in a most restricted fashion:
1st. That the quantity of heat produced by the friction of bodies, whether solid or liquid, is always proportional to the quantity of force expended. And,
2nd. That the quantity of heat capable of increasing the temperature of a pound of water (weighed in vacuo, and taken at between 55° and 60°) by 1° Fahr. requires for its evolution the expenditure of a mechanical force represented by the fall of 772 lb. through the space of one foot.
At the wish of the committee of referees, Joule suppressed a third proposition, to the effect that “friction consisted in the conversion of mechanical power into heat.” But he could not quite bear to leave it out of a footnote.
Even though this measures quantities of heat by dimensions drawn from mechanics, the historian must, nevertheless, respect this restraint, and attribute to Joule, not the enunciation of energy conservation in general, but the narrower demonstration of the mechanical equivalent of heat. Its importance is an illustration of the gathering domination of science by the laboratory. Joule could report constant and definitive results only in 1849. Two years earlier Helmholtz in his memoir On the Conservation of Force, which did announce the principle in full generality, still regarded Joule’s work as peripheral and uncertain. And in an earlier paper Joule himself included more interesting speculative remarks.
A short letter to the Philosophical Magazine of 1845 assumes, by way of a postscript on the “absolute quantity of heat in matter,” that the expansibility of elastic fluids is a consequence of the centrifugal force of “revolving atmospheres of electricity.” Joule seems to mean that these surround each molecule. The pressure will be proportional to the total vis viva of these atmospheres. From the ratio 480:481 of gas pressures at 32° and 33°, Joule estimated absolute zero to be 480° below freezing.
We see then what an enormous quantity of vis viva exists in matter. A single pound of water at 60° … must possess a vis viva equal to that acquired by a weight of 415,036 lb. after falling through the perpendicular height of one foot. The velocity with which the atmospheres of electricity must revolve in order to present this enormous amount of vis viva must of course be prodigious, and equal probably to the velocity of light in the planetary space, or to that of an electric discharge….
But Joule’s was not the mind to pursue these interesting thoughts, and though he dealt from time to time with electrical and chemical forces, no economical statement of conservation beyond that of heat and work escaped his pen.
Very different considerations led J. R. Mayer to similar results in a pair of papers published in Germany in 1842 and 1845. Joule did not then know those essays. Nor, perhaps, would his work have been less independent if he had, so alien was the manner of reasoning, so speculative and metaphysical the thought. For Mayer was a Kantian. He derived the mechanical equivalent of heat algebraically from the gas laws under the inspiration of a highly idealistic metaphysics of causal force. It is scarcely surprising that his work was less appreciated than the mundane measurements of Joule. Mayer’s mind collapsed for a time in the 1850’s, under the strain (it is said) of non-recognition and after an ignoble dispute with Joule about priorities. What seems more likely to one who has read his correspondence is that an emotionalism in his nature went deeper than chagrin, and that introspective brooding was the source of his entire train of ideas as well as of his momentary madness. Mayer was a medical man, a doctor of Heilbronn, specially interested in physiology. Like Darwin’s, his interests were formed by meditations pursued during a tropical expedition which he served as medical officer. A sailor fell ill of some lung disease. Mayer bled him, observed that venous blood was a brighter red in the tropics, much closer in color to arterial, and concluded that metabolism drew less oxygen from the blood in hot climates because maintenance of body temperature required less heat.
In that phlebotomy began a lifelong concern with the conversion of forces, always oriented toward understanding the passage of inorganic into vital forces through metabolism. “Forces are causes,” he wrote in good Kantian style at the outset of his first paper, Notes on the Forces (Kräfte) of Inorganic Nature. “We may, therefore, apply literally the principle, causa aequat effectum. If the cause c has the effect e, then e equals c”; and forces may no more be lost than may the sides of a true equation cease to equal one another. For causes are quantitatively indestructible objects, which (unlike matter) have the additional property of qualitative variability; and this is why it is to forces that we must look for that combination of conservation and change which is reality in action, instead of just in being.
Force and matter, action and being—Mayer announces his metaphysical position right from the start. These are the two great categories into which fall all causal entities. Matter has extension and weight. Its conservation no longer arouses doubt. For force, on the other hand, the negative property of imponderability has generally sufficed. But forces, too, must serve the causal principle (which in Mayer is simply sufficient reason by another name), and must, therefore, be “indestructible, variable, imponderable objects.” Mechanics offers a familiar special case—the conservation of vis viva. Beyond this, chemistry, electrodynamics, and engineering contain many vaguer indications that heat consists in motion. What Mayer calls Fall-Force (Fallkraft) and motion (Bewegung) seem to disappear, only to reappear as heat. Now, to translate Fallkraft at this juncture as potential energy would be like looking up the answers before doing the problem. It would conceal the difficulties that Mayer faced and half-resolved. For though Mayer did express in symbols the quantity now written as m×g×s, equated to the other quantity ½ m v2 (where m is mass; v, velocity; s, a height; and g, the gravitational constant), nevertheless the word he uses for kinetic energy is not the restricted vis viva of mechanics, but rather Bewegung, motion in general considered rather as a quantifiable object than as a state of changing spatial relations among bodies. Bewegung is force, he will assert at the outset of the 1845 essay. It is the parent of all forces. And all this seems very obscure, until one appreciates that Mayer was, nevertheless, perfectly clear about the problem—as clear as Joule and far more interesting, however archaic his terms. That problem was to find what amount of heat corresponds to some certain quantity of Fallkraft or Bewegung, “for example, how high a standard weight must be raised above ground level, so that its Fallkraft should be equivalent to the heating of an equal weight of water from 0° to 1°?” And in 1842 he gave the answer as 365 meters.
Mayer derived this result from the difference between the specific heat of gases at constant pressure and at constant volume. The difference had been determined by Gay-Lussac in 1807, and the data refined by Dulong over the next fifteen years. At constant pressure, about forty percent more heat is required to raise the temperature of a gas than at constant volume. Mayers’s reasoning was admirably original. The extra increment of heat expands the gas against the pressure of the atmosphere. The 1842 memoir was cryptic in the extreme and withheld the computation. The second paper of 1845 is fuller and more generous with numbers. Mayer performed no experiments himself. But he expressed the ratio of specific heats in general algebraic terms, substituted the best figures from the literature on gases, and arrived at the result that,
1° of Heat = 1 gram at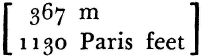 
Elevation, to which a footnote compares Joule’s results as of 1845, which in these terms reduced to 425 gram-meters. (A text book of our own day by Gerald Holton, who writes in awareness of the history of physics, converts Mayer’s result to 3.6 × 107 ergs for the mechanical equivalent of the calorie, and points out that the modern value is about 4 × 107 ergs.) These were positive results. The expression
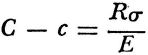
became known as Mayer’s relationship in the developing structure of thermodynamics. The left-hand side is the difference between the two specific heats, and on the right, E is the mechanical equivalent of heat, R the c.g.s. quotient of absolute temperature over atmospheric pressure, and σ the volume of one gram of gas, the latter two quantities being taken at o° centigrade and 760 mm of mercury.
In continuing contrast to Joule, Mayer was drawn on by implications that went deeper than mechanics into the working of nature. He is, indeed, best understood as a medical physicist. The title of his 1845 treatise is Organic Motion in Relation to Digestion. Applied mathematics (he begins) has assumed the leading role in the sciences during the last century. Only biological studies have failed to draw profit from the discoveries and methods of a Galileo or a Newton. As yet, no formulas apply to living nature. The old proverb seems to hold good, by which “The letter killeth, but the spirit giveth life.” And it would be the study of motions in the organic realm that would close up the gap between physics and physiology.
Mayer might almost be mistaken for a Lamarck of physics. He is concerned with activity, not with things. He adduces chemistry as the most familiar example of constant quantities persisting through qualitative changes in form. He sees the mechanical equivalent of heat as simply an instance of the indestructibility of “force.” Given the gas laws and attendant data, it happens to be readily computable. And Mayer went on from there to classify the forms of force. Fallkraft and Bewegung are mechanical cause-and-effect; heat, magnetism, and electricity are imponderable forms of force. Electricity overlaps the category of chemical force. All pass without loss or gain from one form to another in the processes of the universe, wherein the total reservoir of force is inexhaustible and unchanging. And the argument of the treatise tells how plants draw force from sunlight into the organic order, and how animals in turn feed upon the store of force in plants. What expansibility is to gases, the property of chemically transmuting organic into mechanical motions is to living tissues. Mayer considers individual organisms as living heat engines, so to say. His treatise is an essay in the energetics of metabolism. For this was how he meant it: to quantify that about organisms which can be quantified, balancing intake with expenditure of force. And his physiology is valuable, not as the refuge in science of the inexact and the ineffable, but as an arena of exact processes, where all conversions make a perfect fit. He would enrich physics by addressing dynamics to life processes, and complementing the abstract mechanics of extended bodies with a living science of forms and numbers.
The comparison to Lamarck must not be pressed, therefore. Mayer intended no escape from numbers. This respect for numbers, indeed, is what distinguished Kantian idealism from Goethean romanticism in science. It is a distinction central to the proper appreciation of nineteenth-century science in its cultural implications. For Mayer was an idealist but no romantic. He never retreated into the organismic metaphor. Rather he mounted a counter-offensive of physics against Naturphilosophie into the realm of biology. But Mayer’s was physics with a difference. For Mayer did found the philosophical protest against mechanics which would find a richer way for physics, not in biology, but in energetics. Mechanics, in Mayer’s view, was true, but limited by its own abstractions to objects that are extended. It handles only matter, in place or in motion, and the relevant kind of mathematics is analysis of spatial relations by geometry, or its slippery offspring, calculus. But forces, too, are causes (for in Mayer’s world the strictest causalism rules). Forces, too, are objects—imponderable objects, it is true, but objects nonetheless. And where Mayer improves upon others who would handle imponderable objects—electricity, caloric, aether, or whatever—is in distinguishing forces ontologically from matter. No subtle fluids for him: “There is no immaterial matter,” he says severely, laying it down as a principle of sound science. In his work (and this is its originality) the quantities that were to become energy differentials part company with the ineffable eighteenth-century fluids imagined to convey different sorts of action. And it is precisely in assigning fundamental ontological status to force, equivalent to that which monistic mechanism vests in matter, that Mayer penetrated beyond classical physics.
Beyond it, or perhaps back to its source, for in a very discerning passage Mayer invokes Newton’s distinction between a mechanical and a mathematical force. Like gravity, heat is to be treated as a mathematical, but not a mechanical cause of motion. For Mayer was no reductive philosopher assimilating heat to the corpuscular philosophy. His numbers express equivalences rather than levels of analysis. Unlike other critics of caloric, he seems neither to have studied Carnot, nor to have wished to make heat into vibration in the particles of matter. He located the realm of the imponderable and continuous object which was heat deeper than a hypostatic fluid, and made it more fundamental than oscillations. Heat is an expression of force, to be studied by a new physics of forms. For the numerical correspondences between the forms of force are constant and exact. And in Mayer, mathematical physics was something other than the analytical or geometric resolution of the dimensions of bodies in Euclidean space. For him all space is Lebensraum rather than extension. Its mathematicization consists in fixing the numerical equivalences of forces, considered as objects of which the quantities are intensive rather than extensive. In his imagination, indeed, mathematical physics became a numerology of the forms of force, a science at once quantitative (in the amounts) and qualitative (in the manifestations). The mechanical equivalent of heat was only the point of departure. The latter part of his essay computed the consumption of heat and the expenditure of work represented by a variety of objects and events: weights of coal, acts of draft-animals, chemical reactions, electrical, occurrences, contractions in muscle-tissue, and incidents depending for power on metabolism. And the very last sentence foretells how energetics, insofar as it followed Mayer in spirit, would seek to inform a physics, fragmented by the atomizing touch of kinetics, with a renewed sense of an ideal unity in the activity of nature: “Only in the cooperation of all instruments lies harmony; in harmony alone lies life.”
CONSERVATION of Energy as a principle lurked (to give technology its due) everywhere latent in the steam. It has played a fundamental role, the most fundamental as some would say, in the last half-century of classical physics, and since then in quantum mechanics. Sooner than give it up, Poincaré once remarked, we would imagine new forms of energy to save it. In the neutrino, indeed, nuclear physics did just that. Yet it is a curiosity that this, which is the first law of thermodynamics, should have so fruitfully watered the stonier, the more austere terrain of mechanics. “By what magic,” asks Bridgman, “has our stream risen higher than its source?”—in defiance, as it were, of some intellectual application of the second law. The answer may be historical. Historically at least, the growing appreciation of the first law and its scope owed much to the urbanity and economy of Helmholtz’s beautiful memoir of 1847, On the Conservation of Force. His was perhaps the most gracious personality of nineteenth-century science. Though he devoted much thought and effort to lectures on popular science, his advocacy never transgressed bounds of good taste in the insistence of a Tyndall, the too conscious cleverness of a Huxley, or the romantic brutality of a Haeckel. Nor did his authority chill, like the Gallic hauteur of a Claude Bernard. In Helmholtz, German warmth and naturalness appear at their best, lending a welcome serenity to a fine physical intelligence and civilizing science by passing it through a cultivated mind, alive with a sense of cultural responsibility.
For Helmholtz’s was a tranquil talent. It indicates how recently science has become professional that this man, in his thinking the most universal of the nineteenth-century physicists, should have been trained for medicine, and begun his career as a Prussian army doctor. No doubt this unspecialized approach, in which his generation was the last to feel at ease, held its own advantages. The range of Helmholtz’s contributions runs from physiology through physics to philosophy. He invented the ophthalmoscope, which reflects the examining physician’s beam of light through the pupil onto the retina and permits his own observation through the hole in the center of the parabolic mirror. Helmholtz had been trained under Johannes Muller in Berlin, and had been much impressed by his demonstration that many sensations are specific rather to the nerve than to the stimulus. Studies of the retina led Helmholtz into the physics of perception, first of light and then of sound, and by a kind of German instinct for harmonies (that which Mayer, too, expressed) Helmholtz applied optics to the elucidation of beauty in paintings, and acoustics to the recognition of loveliness in music. The problems of perception, finally, brought him back to epistemology and the philosophy of science, where his education had begun. There his dissatisfaction with Hegelian process, its affirmation of spiritual absolutes as against science, led him to look behind romanticism to rationalism and Kantian idealism as the guide in science itself.
Helmholtz was more explicit than Mayer, and more aware of the difficulties. In conservation of energy, he made his most comprehensive statement. Helmholtz, too, came to it from physiology. His earliest researches investigated the quantity of heat generated by laboratory animals, and found it equal to that produced by burning their food in a calorimeter. Thus metabolism is oxidation rather than soul at work. But this was preaching to the converted, for the most part, and what marks Helmholtz is the comprehensiveness of his reasoning, and the form he gave it. When he published On the Conservation of Force, he was twenty-six years old, and still tending the ailments of Prussian conscripts. A memoir of some sixty pages, it is certainly the seminal work of his life. Unlike Mayer, Helmholtz enlisted the forces of nature in the service of mechanistic images. Instead of beginning with heat, or force in general, he went back to classical eighteenth-century dynamics, started with its fundamental principle, the conservation of vis viva, and assimilated heat to that by applying conventional analytical mathematics to problems of energy. For though not a creative mathematician, he was gifted with a powerful mathematical grasp, and with the skill, becoming essential to him who would be a creative physicist, to wield the sharpest weapons available in the mathematical armory of his day. And he couched his discussion in the most sophisticated language known to physics, not all weighted down by lumps of data like Joule’s heavy-handed laboratory reports, nor confined to the primitive numerical equivalences of Mayer, but in the graceful, taut, and lissome differential equations of classical dynamics.
The introduction purports to eschew philosophy in favor of a “purely physical hypothesis.” But in the very act of repudiating philosophy, it becomes clear how Helmholtz (like Mayer) had formed his expectations about science along Kantian lines. Experimental science, he explains, groups phenomena together descriptively under general rules. The law of refraction is one example. The gas laws are another. Theoretical science, for its part, seeks to grasp phenomena in accordance with causality and sufficient reason. It is a study which is, so to say, enjoined on man, a thinking being, by the axiom: “Every change in nature must have a sufficient cause.” We are bound to pursue investigations until we discern the invariant cause, which we distinguish from effects precisely by its constancy. Not that science presumes to embrace all facts, or to assert that nature is wholly intelligible. Perhaps there is in things a domain of spontaneity, of liberty. But the limits of causality are limits of science.
Within that domain, science contemplates the objects of the world under two points of view, in their existence and in their activity. Matter is the abstraction which we make in classical mechanics of the existence of bodies. It has the properties of extension and mass. Its quantity is constant through all eternity. But—Helmholtz, too, brings us to the point where energetics penetrates beyond the Democritan world picture—we cannot reduce qualitative differences in objects to changes of position in matter. And force is the abstraction which we make of the cause of events. What with his emphasis on causality, Helmholtz directed theoretical (as contrasted to merely experimental) physics rather toward force than matter. Helmholtz and Mayer were moving under the same inspiration, therefore, but Helmholtz occupied the new ground with far greater assurance. And in the minds of both these German thinkers, it was the Kantian identification of cause and effect in the intellectual effort of theory which raised force to a status equivalent to that of matter—equivalent ontologically but more interesting physically. Thus the types of force (vis viva, heat, chemical bonds, electricity, magnetism, gravity, and perhaps others yet unperceived) were to be objects of science equally with the kinds, pieces, and locations of matter. Matter and energy were to be the two aspects of that which has been from everlasting to everlasting, instead of just matter in motion (where force is but the poor thing, mass times acceleration).
The pattern is classic. For no one has ever discovered conservation (of whatever) in some experiment. Rather, conservation has always been assumed as a condition of objective science. Confidence in it rests on the whole experience of science in its history, which may even be seen as the extension of such considerations over ever widening areas of nature. The laboratory may, indeed, provide reassurance that conservation is served in some certain set of experiments, but it is not found there where Priestley found oxygen, Newton the composition of light, and Becquerel radioactivity. Instead, the theorist assumes it, as Lavoisier did, in order to rationalize and control experience. It is meaningless, therefore, to ask who discovered the conservation of energy? No one did. Helmholtz’s was a more difficult achievement. He expressed what everyone was vaguely assuming. And the decisive element in his success was that he alone began, not with heat or force (the unknown), but with motion (the known). Motion is the one instance of regular, lawful change of which matter per se is capable. The most general principle of dynamics is conservation of vis viva. The problem, as Helmholtz saw it, was to extend the laws governing spatial rearrangements to the parallel domain of forces, of assimilating (as he might have said) the activity of nature to the laws that govern its existence, or (as we might say) of embracing energetics in the formalism of mechanics, where conservation already did obtain:
Unless theoretical science is willing to remain where it is, half-way towards understanding, it must harmonize its views with the requirements of this principle [of conservation of vis viva] as to the nature of elementary forces, and also with the consequences. The mission of theoretical science will have been accomplished when it has defined all phenomena in terms of elementary forces, and demonstrated that this definition alone is compatible with the facts. Such a definition should be considered as the necessary form in which to conceive nature. It may be awarded the status of objective truth.
Mechanics offered Helmholtz a sure footing to raise him above the standpoint of Joule and Mayer, who were pulling a science of thermodynamics up from the study of heat by its own bootstraps, the one experimentally and the other metaphysically. And now the threads twisted together by modern physics begin to be discernible, and it becomes evident how it was that conservation of energy, become so fundamental in later mechanics, appeared historically as the first law of Thermodynamics. For the axioms and the equations actually came from mechanics. But the object of reasoning was energy, and pursuing that (as yet unnamed) object, Helmholtz looked for guidance right into the heart of the problem itself, neither back to mechanics (which would have led him in a circle to his starting point), nor to Joule or Mayer (confined to their subordinate considerations), but rather to Carnot and Clapeyron, who alone had studied the mechanical power of heat theoretically.
Theirs are the first names to appear in the argument, which starts from the assumption
that it is impossible to create a lasting motive force out of nothing by any combination of bodies. By means of this principle Carnot and Clapeyron have already demonstrated theoretically a series of laws, some already known to science, others not yet confirmed by experiment, concerning the latent and specific heats of the most diverse bodies in nature.
Now, the impossibility of perpetual motion was nothing new. Before the Revolution the French Academy of Sciences had haughtily refused even to notice any more inventions purporting to yield something for nothing. But the despair of perpetual motion rested on nothing deeper than the inevitability of friction. It served scientists only by saving their time. Carnot’s theory made it interesting. He employed our incapacity positively, as an instrument of reasoning by exclusion of the inadmissible. He said, not just what we cannot do, but what heat will do, and he laid down the condition of a temperature differential. And now Helmholtz seized on this advantage as on the one device that might lead outward from dynamics to his goal, a generalization of conservation, beginning with vis viva but covering heat and all other manifestations of what he (and therefore we for yet a little longer) must still call force.
Thus Helmholtz prepared dynamics to serve his purposes by first importing into it the analytical device which Carnot had fashioned of the concept of reversibility in a conservative situation. By the same token, moreover, he liberated the argument from its dependence on the caloric theory of heat, and clothed it instead in the strong authority of classical mechanics. We are to imagine a system of mass points acting under reciprocal forces. In passing from one configuration to a second, the points acquire velocities which may be exploited to do work. To draw the same quantity of work a second time from the system, one would have to restore the initial conditions by some means, by expending on it, for example, energies drawn from outside the system itself. Now, it follows from the axiom that the work consumed in thus going backwards equals that created by the initial process, regardless of what means are employed, what routes are followed by the particles, or what the velocity is in either direction. If it were not so, one could choose one route, say, in preference to another, in order to profit from the difference. Thus could one create perpetual motion, the inadmissible. The mathematical expression which excludes that impossibility is simply the law of the conservation of vis viva, and since we knew this result in principle all the time, what we have won is confidence in the argument.
Helmholtz now extends that argument. The product of force into distance had been tacitly adopted as the measure of power in the theory of machines. Helmholtz combined it with the gravitational constant in order to equate the work expended by a freely falling body with the vis viva acquired. Since the velocity which a body must attain to reach some height, h, against gravity is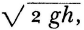 
then
m g h = ½ m v2.
Next, Helmholtz pauses to show analytically that any system of mass points in which conservation does hold must be subject only to radially directed forces among the particles. Nor is this a digression, for Helmholtz never let the goal of generality slip from sight. But so tightly knit is the structure of his thinking that one must look closely to discern the articulations. What he has done combines the measure of work taken from the theory of machines with the conservationist reasoning of the Carnot memoir on heat to define force in general as the capacity to do work. But so far the argument reaches only the gravitational case. The equilibrium considerations involve gravitational force as that against which work is done, and make conservation of force identical with the principle of virtual velocities. That is to say, vis viva is by now translatable as kinetic energy, but the concept of potential energy had still to be distinguished from the pull of gravity.
The second chapter achieves that abstraction. Now we profit from the demonstration that only central forces operate in conservative systems of point-masses. For gravity, therefore, (which is itself a central force in a conservative system) may be substituted the “tensions (verbrauchten Spannkräfte) which correspond to the relative variation of the distance to the center of force.” Then, an increase in the vis viva of a mass point under any conservative central force equals the decrease in this “tension,” or when ϕ is tension, q velocity, and r the radial distance to each center of force,
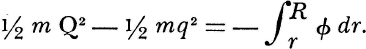
The words had still to be. attached. “Work” was regularly used for Carnot’s motive power only by Clausius, after 1850. Half a century earlier Thomas Young had proposed “energy” as a term less anthropomorphic than vis viva, and as denoting a dynamical quantity different from Newtonian force. But the word never caught until revived by Rankine, who borrowed from electronics the qualifier “potential” with which to couple it in replacing Spannkraft for the right-hand side of the equation. Kinetic energy, on the other hand, owes its characterization to the determination to keep the left-hand side of the energy equation within the reliable domain of corpuscular mechanics, where it succeeded to vis viva.
Helmholtz wrote without benefit of these terms in his first edition, but surely we are by now entitled to anticipate them in order to do justice to the clarity with which he disentangled the quantities concealed amidst the residues of common usage, Newtonian accelerations, and engineering practices, in order, too, to appreciate the finesse with which he wrested a statement of the conservation of energy from the elusive, the almost tautological quality of the notion of force. For this equation is the first expression that contains the full meaning of energy. Kinetic energy is expressed as a difference in levels, and that difference is equated to the definite integral of the “available tensions capable of producing such a certain effect.” Nor, though Helmholtz addressed this memoir to the Physical Society of Berlin, was mid-nineteenth-century physics yet so far gone in mathematicization that he did not also express his law in the less economical form of words:
In all cases of motion of material points under the influence of their attractive or repulsive forces, of which the intensity depends only on distance, the decrease in tension [potential energy] always equals the gain in vis viva [kinetic energy]; and contrariwise, an increase in the former equals a loss of the latter. In other words, the sum of vis viva and tension is always constant. In this its most general form, we may designate our proposition as the law of conservation of force [energy].
One feature of the history of concepts on force and energy is the narrowness of the area for maneuver between assumptions and conclusions, and the mind unused to these reflections sometimes finds it difficult to perceive in what respect the one goes beyond the other. The decisive element in Helmholtz’s argument is the assurance with which he built out from axioms of dynamics, reasoned by analogy about heat, electricity, and chemical energy, and then re-imported his findings back into the sure subject of mechanics to verify their validity. Thus, it is no tautology when the first use that Helmholtz makes of his powerful new law of conservation of energy is to derive from it, as a special case, the principle of virtual velocities, perhaps the best established and the simplest proposition, one will not say of mechanics, but of statics. For he is not in fact thinking in a circle. Rather, he is verifying his law by a thought experiment, showing that what we cannot doubt is a special instance of a new hold on a wider reality. And armed with this reassurance, he restates the conclusions about work which Carnot had rested upon conservation of caloric. But now he puts them in terms of rational mechanics, and derives them from the conservation of energy instead of the indestructibility of heat as a fluid: 1) In a system where energy is conserved, the maximum work obtainable is finite and determinate; 2) If non-conservative forces existed, which did depend on time or velocity, or which acted other than radially, then combinations of bodies could create or destroy energy, which result is inadmissible—ergo such forces do not exist; 3) A system in equilibrium under central forces could never be set in motion relative to other systems by internal, but only by external forces—in other words, nothing is self-starting.
The remaining chapters read the law in analytical detail into the several departments of physics. First, theorems of mechanics are made to follow: the inverse-square relationship of gravity; the popular rule that loss of force in simple machines is proportional to velocity acquired; the kinematics of elastic bodies—wave mechanics, impact, the reflection and refraction of light, the velocity of sound. Next, heat is treated explicitly as a form of energy, and its mechanical equivalent is established theoretically. And in this, the most important connection historically, it is quite clear from the first edition that the historian is to present Helmholtz rather as parting company from Carnot on the nature of heat, than as conceptualizing the measurements of Joule. Joule’s results were too imprecise to inspire confidence in 1847, and it is not because of them that Helmholtz, too, defines “Quantity of Heat” as only a means of expressing “the quantity of the vis viva of the calorific movement, or on the other hand, of the Spannkraft of the atoms.” And he goes on to sketch out qualitatively the way in which such energy is distributed among the three degrees of freedom which, in a moment of profound insight, Ampère had imagined to exist for molecules.
The adaptability of concepts of potential to energetics suggests the importance which electricity was assuming in all of physics. Helmholtz very deftly reduced the motion of electrical and magnetic charges to the formalism which mechanics had developed for material masses of corpuscular texture. It was less fortunate, perhaps, that he also organized his electrodynamical discussion in a fashion reminiscent of the eighteenth century. Thus, electricity has two modes of motion. It may be transported along with supporting bodies (static electricity). Or it may move through such bodies (galvanic electricity). In the latter case, the electric current may be conducted either metallically or chemically in electrolytic solutions. In all cases, Helmholtz balanced the heat generated by currents against its mechanical equivalent, and compared chemical and electrical energies by reference to their thermal equivalents. The induced current was still too novel to be handled with familiarity, and Helmholtz treated it separately, less for its own sake than as a means of including magnetism within energetics through its convertibility to electricity. There remained, finally, the whole of living nature. Plants accumulate large stores of chemical energy, converting it (so far as one can tell) from no source other than the vis viva of rays of sunlight. Animals have this to draw upon to fuel their own metabolism. Like Mayer before him, Helmholtz ends as he began, with the energetics of physiology. But Helmholtz only gestures toward biology, for science as yet furnished few data from which to compute equivalents.
Years later, and in popular lectures, Helmholtz became one of the most eloquent preachers of the gospel of energy. For the first law became the favorite text for the sermons on science which fill a large, and in the case of Helmholtz a not too desperately unreadable, literature in the late nineteenth century:
From a similar investigation of all the other known physical and chemical processes, we arrive at the conclusion that nature as a whole possesses a store of force which cannot in any way be either increased or diminished; and that, therefore, the quantity of force in nature is just as eternal and unalterable as the quantity of matter. Expressed in this form, I have named the general law “The principle of the conservation of force.”
We cannot create mechanical force, but we may help ourselves from the general store-house of nature. The brook and the wind, which drive our mills, the forest and the coal-bed, which supply our steam engines and warm our rooms, are to us the bearers of a small portion of the great natural supply which we draw upon for our purposes, and the actions of which we can apply as we think fit. The possessor of a mill claims the gravity of the descending rivulet, or the living force of the moving wind, as his possession. These portions of the store of nature are what give his property its chief value.
In a curious way, the central ideas of thermodynamics when traced historically lead, not to each other, but back to Carnot’s memoir. It is a science shaped, as compared to others, more by intellectual heredity than by experimental environment. Thus, Joule and Mayer established the convertibility of heat and work quite independently of each other, in quite different ways, but both of them in the course of arguments intended to be crucial against the materiality of heat. Helmholtz began with neither argument, but rather with Carnot’s own proof of the necessity for a temperature differential, and with the exclusion of perpetual motion. In one respect, indeed, Helmholtz did less with that analytical device than had Carnot. Helmholtz transposed the impossibility of perpetual motion into terms of mechanics, where it had long been assumed, in order to invest the new study of heat with the authority of mechanics. Nor so long as it was a question of work into heat could thermodynamics embarrass a mechanistic science. The kinetic energy of a piston could plausibly be imagined to impart equivalent energy of motion by impact to molecules of a gas. Helmholtz was quite indifferent to questions of direction. He reasoned rather about work into heat than heat into work. Nor did he at first remark that the case for mechanism is far more parlous when the latter is the direction of conversion. For by Carnot’s own principle, not all the heat reappears as motion, but some of it is carried down from the higher to the lower temperature, where like a Cheshire cat it simply disappears. In a word it is consumed. And though it may thus serve conservation within some wider set of boundaries, vanishing does not on the face of it conform to corpuscular mechanism.
Two new quantities follow historically from the Carnot temperature differential—absolute zero and entropy. The existence of a bottom to temperature had been implied in Carnot’s discussion, as in Mayer’s, of the difference between specific heats at constant pressure and volume. But William Thomson first investigated the data experimentally, and fixed the value at minus 273°, where molecules cease to move. He became Lord Kelvin in honor of his distinction in the laboratory—hence the name of the absolute temperature scale. Thomson did for temperature what Carnot had done for heat. He considered its quantity independently of the physical properties of mercury, alcohol, or any particular substance of which the expansion might be measured on a thermometer. He too began directly from the Carnot memoir, of which he seems to have thought himself in some sense the discoverer. Moreover, he saw the difficulty introduced into Carnot’s conservation of caloric by the Joule-Mayer demonstration that heat is lost to mechanical power. Nor does the flow of heat necessarily do work. It does none, for example, in simple conduction. Nevertheless, Thomson was unwilling to do without the temperature differential as the source of motive power. “If we abandon this principle, we meet with innumerable other difficulties—insuperable without further experimental investigation and an entire reconstruction of the theory of heat from its foundations.” And rather than accept such a setback, he preferred to despair for the moment of resolving the difficulty between the convertibility of heat into work and its transportation and loss to a lower temperature, which appeared as necessary and mutually exclusive conditions for realizing its motive power.
Rudolf Clausius firmly grasped both horns of this dilemma, refused the alternative Carnot or Joule, and incorporated the essential principle of each into the second law of thermodynamics. “It is not at all necessary,” he wrote in his memoir of 1850, On the Motive Power of Heat,
to discard Carnot’s theory entirely, a step which we certainly would find it hard to take, since it has to some extent been conspicuously verified by experience. A careful examination shows that the new method does not stand in contradiction to the essential principle of Carnot, but only to the subsidiary statement that no heat is lost, since in the production of work it may very well be the case that at the same time a certain quantity of heat is consumed and another quantity is transferred from a hotter to a colder body, and both quantities of heat stand in a definite relation to the work that is done.
The title is a translation of Carnot’s, no doubt designedly. For though Clausius knew Carnot only through Clapeyron’s mathematical treatment, he falls into the pattern by which he and his contemporaries went rather to Carnot than to one another for the ideas they developed. Clausius seems not to have studied Helmholtz closely at this time, nor to have been preoccupied with the work-plus-heat function in which energy is conserved. Rather, he addressed himself to the conversion of heat into work, and its transportation in the process to a lower temperature. Nor did he find the case so desperate as Thomson, who drew from it nothing deeper than absolute zero. Clausius’s was a subtler mind, less concrete than Joule’s or Thomson’s and less comprehensive, perhaps, than Helmholtz’s, but the supplest of their generation in the abstract reaches of physics. And the enigmatic quantity, entropy, awaited his discernment—the second great principle to follow out of Carnot’s reasoning and the complement to conservation of energy. Time’s Arrow, the second law has been called, in the lapidary phrase imagined by Sir Arthur Eddington to evoke the consequence that in this principle physics first found a difference between time past and time future. In it the history as well as the structure of nature becomes capable of physical description.
Clausius seized upon the point that Carnot’s essential principle was not the conservation of caloric, but the unique dependence of the motive power of heat on T2 and T1. His was a different problem, therefore, from Helmholtz’s. He analyzed not what was conserved, but what was lost, thus distinguishing between that portion of heat which disappeared at the lower temperature and that which converted into mechanical work according to Joule’s ratio. It would be tedious to travel isothermally and adiabatically around the Carnot cycle once again, even to survey the changes through Clausius’s more sophisticated eyes. He took full advantage of the cyclic device, which cancels out the effects of intermediate internal changes, so that all the work done or heat consumed represents external effects. And he observed that the necessity to consume heat or expend work introduces an asymmetry into the restoration of the initial conditions. The system is back in the same state at the end of the cycle, but something has changed, something not material has disappeared, something inaccessible to conservation laws. That something is amenable, however, to Carnot’s principles. Its quantity depends only on the initial and final states of the system, and not on the intervening routes or rates. What has occurred has done so by means of a temperature differential.
The measure of what has changed is entropy. Clausius identified that quantity only later, in a paper of 1854. It will be well to indicate the derivation. Clausius denotes by Q1 the quantity of heat drawn from the heat reservoir at T1; by Q, the amount converted into work; and by Q2, the amount which passes down to the sink at T2. Then
Q1 = Q2 + Q,
and
where ϕ (T1, T2) is some function of the temperatures, which is independent of the nature of the body. By the latter condition, what is true of any body must be true of all, and it is permissible, therefore, to consider the case of an ideal gas. It can be shown from the gas laws that
Now, we may adopt the convention that heat taken in is positive, and heat given out, negative; then the sign of the second term changes, and
The same reasoning applies to a reversible cycle of any number of stages and temperatures:
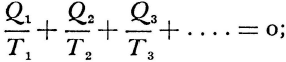
or,
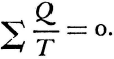
Finally, we may consider cyclical processes of general form. Even though not consisting of successive isothermal and adiabatic stages, they may nevertheless be analyzed in terms of infinitesimal elements of such lines, so that
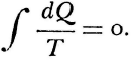
In words, this relation would be:
If in a reversible Cyclical Process every element of heat taken in (positive or negative) be divided by the absolute temperature at which it is taken in, and the differential so formed be integrated for the whole course of the process, the integral so obtained is equal to zero.
From the conditions of a cyclical reversible process, it follows that the expression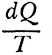 
must be the differential of a quantity which depends on the configuration of the system, but which is altogether independent of the manner in which that configuration has come about. If we call this quantity S, then
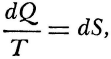
or
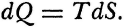
Clausius coined the word entropy for S: “I prefer going to the ancient languages for the names of important scientific quantities, so that they may mean the same thing in all living tongues. I propose, accordingly, to call S the entropy of a body, after the Greek word ‘transformation.’ I have designedly coined the word entropy to be similar to ‘energy,’ for these two quantities are so analogous in their physical significance, that an analogy of denomination seemed to me helpful.”
Two laws now describe the energetic state of a system. The first (dQ = dU + dW) says that energy is conserved. The second (dQ = T dS) says that in a real—i.e. irreversible—process, entropy increases; or that energy (however faithful to conservation) becomes increasingly unavailable in the way in which nature does in fact move. And the idea of entropy has proved a very acute instrument of analysis. For although thermodynamics per se knows only reversible processes, the second law evades this limitation by measuring the unavailability of energy, the departure of the real from the ideal, the brake (so to say) of friction between things, rather than the inertial persistence in them. This back-handed approach made it possible to consider irreversible and reversible processes in the same formalism. Nor need a reversible process be cyclical for the second law to obtain. Two particular configurations of a system might be considered as a “state-couple,” in which case one need not return the system to the starting point to analyze it, provided one accept the wider condition of considering only the initial and final states, and not the manner of the transition.
IN THE ANALOGY between energy and entropy, Clausius hoped to save the mechanical theory of heat from the contradiction between its conservation as energy and its consumption in work. It was a plausible hope. His enthusiasm is infectious and persuasive. Both energy and entropy are functions rather of the state or organization of things than of their mass, location, or extension. Neither one is a measure of materials. Neither one is a point function. Both have significance only in comparison to a previous value, since both are defined with reference to the initial and final configurations of a system, instead of to its instantaneous condition. Both of them, moreover, are highly sophisticated and abstract representations of certain elementary experiences of the world, certain serious intuitions: Energy, of the intuition that there is an activity, a “force” in things beyond matter in motion, that something real makes nature go (and all history teaches that if this be so, then the assumption of conservation is a pre-condition to embracing it in measurement, which is to say in science); Entropy, on the other hand, of the complementary experience of water seeking its own level, of hot bodies cooling, of springs untensing, of magnetism wearing off and electrical charges leaking away, of a destiny such
That no life lives forever;
That dead men rise up never;
Winds somewhere safe to sea;
of a world getting old and running down.
Nevertheless, the analogy between energy and entropy has not always sustained the weight of Clausius’s hopes. It should by now be evident that a certain philosophical confusion hovered over the enunciation of those quantities, symptomatic (it may be) of the formalism of the likeness. There was Clausius himself, for example, saving the mechanistic theory of heat in a concept derived from the unmechanizable fact of the necessary loss of heat on conversion into work. There were Mayer and Helmholtz, conserving “force” on the grounds of strict causalism, which was to say sufficient reason, and to that end promoting energy to ontological partnership with matter—and assigning it a status opposite atoms comparable to that occupied by the void in the old corpuscular philosophy. Across the Channel, on the other hand, where that philosophy still informed the style of science, Joule instinctively conserved energy as vis viva—not as metaphysical cause, but on the classical grounds of dynamics.
Moreover, whatever standing one might assign to energy, surely entropy could never be ontologically equivalent. It is too arbitrary and unreasonable a concept. It is an abstraction, not from the measurement of objects of some sort, but from the inability of nature to swim upstream in time. Whether entropy be called positive or negative is a mere convention. Like the working of the steam engine from which the Carnot cycle was abstracted, entropy has reference only to gross processes and never to deep structural relations in nature. It is no measure of particular things, but an index to the condition of a crowd of things, or rather to how its condition has compared or will compare. The reasoning is all about reversible processes, but the finding is that no real process is reversible: we learn about the real by contemplation of the impossible. It seems odd that a fundamental law of nature should rest upon the exclusion of what man cannot do, namely create perpetual motion. Yet there are those (and foremost among them Eddington) who have claimed for the second law the status of the most fundamental among the laws of nature.
The difficulties in the logical relations of the first and second laws go back to a deep inconsequence in the historical order. For the laws of thermodynamics are not like Newton’s laws, or Kepler’s. They are not reducible one to the other. They are not about the same thing. The first law states an ideal equality, and the second law a real inequality. The first law says that the amount of energy in a system is constant, and it emerged historically from discussions of the convertibility of forms of energy, discussions now mechanistic and again idealistic. The second law, on the other hand, says that the availability of energy in a real process decreases, that energy is degraded in nature, that heat is a wasting asset, and that the world is living on its capital. And this finding emerged historically from the fallacy that heat is conserved, which is to say from the experience that it is lost, even though it is a form of energy. By the second law, nature follows a determined direction, or at least a direction so highly probable that were it violated, all our sense of order in things would go with it. And this is irreconcilable with the great concepts of mechanism, in which time is a geometric parameter. In thermodynamics, time was the course of a process once again, as in quite extraneous biological notions of progress and evolution.
Even there, however, superficial conflicts arose to mar a rapprochement which might have lent a new though false vitality to biological romanticism. Uniformitarian geology and Darwinian biology required hundreds of millions of years, perhaps even billions, for the evolution of species by natural selection. In principle, indeed, the nineteenth-century conceptions of earth history followed Hutton in presupposing infinity in time. Not so the physicists, very severe in their new thermodynamics, who in the person of Kelvin would allow the geologists only ten million years since the earth had been molten and a few million more before it would cool to lifelessness under a waning sun. “I take the sun much to heart,” wrote Darwin in dismay, more alarmed for his theory than for his descendants. The second law was even more damaging to the cosmic historicism of Herbert Spencer, who had assimilated the idea of progress to a supposed movement from the homogeneous and undifferentiated to the individualized and the highly organized. For the ineluctable increase of entropy in the universe precisely contradicts this liberal tendency in things.
It skirts tautology to say (as often is said) that entropy is a measure of the disorder or randomness of a system. Nor were all the uses of this quantity imagined until the later decades of the nineteenth century. Since then, entropy has become a protean concept, no doubt because science and philosophy have become more and more preoccupied with problems of organization and information, and less and less interested in classical models of matter, motion, and space. The status, so to say, of energy has suffered from the decline of causalism (true in this retreat to the historical emergence of the first law from the idealist identification of cause and effect in the real), whereas the prestige of entropy as an organizing idea has risen correspondingly. Does it advance upon us along with the disintegration which it indicates? In any case, the fortunes of entropy have expanded along with the probabilistic analysis. Entropy becomes, for example, a measure of the probability of finding a system in such a certain state. And all this decline of dogmatism in classical physics seems curiously reminiscent of the collapse of dogmatism two centuries before, under the erosion of the very Newtonian critique which had established that physics. Indeed, modern philosophy of science sometimes seems like a reprise of the main themes of the Enlightenment. Once again philosophers study the implications of science for the operations of the mind that creates it, for language and communication. In information theory, entropy becomes a measure of the uncertainty of our knowledge. Everything is reminiscent except the mood. For now philosophy teaches us of the difficulty of communication, and not of the educability of man.
But the idea of entropy had already been generalized in the vaguer, the more cosmic pessimism of the late nineteenth-century prophets of despair, for whom the idea of progress had turned to clinkers, and who sat among the ashes contemplating the heat death of the universe. It is odd that this should have been so prevalent a posture at the end of the century. To us it is bound to seem a century which had scarcely known disaster. Indeed, no problem more pressingly invites study than that of the cultural factors which determine what use is made of the ideas and findings of science. And surely the answer will be found in the world of men, and not in the world of nature. For it can scarcely have been science which changed the style from the optimism of the eighteenth century to the callow pessimism of the nineteenth.
Certainly evolution and entropy were the leading novelties which nineteenth-century science offered to the pundit. Exponents of Darwinism, as is well known, interpreted competition in the most ferocious fashion, making strife the law of life, and progress the defeat of the miserable and incompetent instead of the harmonious advancement of mankind along the paths of nature. But Darwin had only found his language in the literature of political economy, where the mood was already fatalistic. Nature holds no such message. Nor, perhaps, is entropy really much help to the understanding of history or the social process. Nevertheless, if the robber baron and the strong man armed took license to ruthlessness from the theory of natural selection, the intellectual who shrank from such successes found in entropy the excuse to indulge his mal du siècle. To Americans, the voice of Henry Adams comes as the most familiar of those speaking out disillusionment from the soured dream of progress. Instead of moving toward the perfection of the race, history runs downhill toward a miscellany of the second-rate, a society without classes, structures, gradations, duties, responsibilities, nobility, or culture, without Mont-Saint-Michel or Chartres. The future, in other words, holds only equality and social randomness. But surely Adams had despaired of liberalism, and of his education, before he lost faith in the universe? Surely he, and his literary contemporaries, accepted with something very like irresponsibility and relief the imminent prospect of an end to time, when though the masses would be one with the fastidious, none would perceive the universal degradation. This, indeed, is the release for which Swinburne praises “whatever gods there be:”
Then star nor sun shall waken,
Nor any change of light:
Nor sound of waters shaken,
Nor any sound or sight:
Nor wintry leaves nor vernal,
Nor days nor things diurnal
Only the sleep eternal
In an eternal night.
