§ 8.—Of the Ancient Practice of Painting.

IF MY READERS have followed me with any attention up to this point, they will not be surprised to hear that life is somewhat dull in Flatland. I do not, of course, mean that there are not battles, conspiracies, tumults, factions, and all those other phenomena which are supposed to make History interesting; nor would I deny that the strange mixture of the problems of life and the problems of Mathematics, continually inducing conjecture and giving the opportunity of immediate verification, imparts to our existence a zest which you in Spaceland can hardly comprehend. I speak now from the aesthetic and artistic point of view when I say that life with us is dull; aesthetically and artistically, very dull indeed.

How can it be otherwise, when all one’s prospect, all one’s landscapes, historical pieces, portraits, flowers, still life, are nothing but a single line, with no varieties except degrees of brightness and obscurity?

It was not always thus. Colour,1 if Tradition speaks the truth, once for the space of half a dozen centuries or more, threw a transient splendour over² the lives of our ancestors in the remotest ages. Some private individual—a Pentagon whose name is variously reported—having casually discovered the constituents of the simpler colours and a rudimentary method of painting, is said to have begun by decorating first his house, then his slaves, then his Father, his Sons, and Grandsons, lastly himself. The convenience as well as the beauty of the results commended themselves to all. Wherever Chromatistes,—for by that name the most trustworthy authorities concur in calling him,—turned his variegated frame, there he at once excited attention, and attracted respect. No one now needed to “feel” him; no one mistook his front for his back; all his movements were readily ascertained by his neighbours without the slightest strain on their powers of calculation; no one jostled him, or failed to make way for him; his voice was saved the labour of that exhausting utterance by which we colourless Squares and Pentagons are often forced to proclaim our individuality when we move amid a crowd of ignorant Isosceles.

The fashion spread like wildfire. Before a week was over, every Square and Triangle in the district had copied the example of Chromatistes, and only a few of the more conservative Pentagons still held out. A month or two found even the Dodecagons infected with the innovation. A year had not elapsed before the habit had spread to all but the very highest of the Nobility. Needless to say, the custom soon made its way from the district of Chromatistes to surrounding regions; and within two generations no one in all Flatland was colourless except the Women and the Priests.

Here Nature herself appeared to erect a barrier, and to plead against extending the innovation to these two classes. Many-sidedness was almost essential as a pretext for the Innovators. “Distinction of sides is intended by Nature to imply distinction of colours”—such was the sophism which in those days flew from mouth to mouth, converting whole towns at a time to the new culture. But manifestly to our Priests and Women this adage did not apply. The latter had only one side,3 and therefore—plurally and pedantically speaking—no sides. The former—if at least they would assert their claim to be really and truly Circles,⁴ and not mere high-class Polygons with an infinitely large number of infinitesimally small sides —were in the habit of boasting (what Women confessed and deplored) that they also had no sides, being blessed with a perimeter of one line, or, in other words, a Circumference. Hence it came to pass that these two Classes could see no force in the so-called axiom about “Distinction of Sides implying Distinction of Colour;” and when all others had succumbed to the fascinations of corporal decoration, the Priests and the Women alone still remained pure from the pollution of paint.

Immoral, licentious, anarchical, unscientific— call them by what names you will—yet, from an aesthetic point of view, those ancient days of the Colour Revolt were the glorious childhood of Art in Flatland—a childhood, alas, that never ripened into manhood, nor even reached the blossom of youth. To live was then in itself a delight, because living implied seeing. Even at a small party, the company was a pleasure to behold; the richly varied hues of the assembly in a church or theatre are said to have more than once proved too distracting for our greatest teachers and actors; but most ravishing of all is said to have been the unspeakable magnificence of a military review.

The sight of a line of battle⁵ of twenty thousand Isosceles suddenly facing about, and exchanging the sombre black of their bases for the orange and purple of the two sides including their acute angle; the militia of the Equilateral Triangles tricoloured in red, white, and blue; the mauve, ultra-marine, gamboge, and burnt umber of the Square artillerymen rapidly rotating near their vermilion guns; the dashing and flashing of the five-coloured and six-coloured Pentagons and Hexagons careering across the field in their offices of surgeons, geometricians and aides-de-camp— all these may well have been sufficient to render credible the famous story how an illustrious Circle, overcome by the artistic beauty of the forces under his command, threw aside his marshal’s bâ-ton and his royal crown, exclaiming that he henceforth exchanged them for the artist’s pencil. How great and glorious the sensuous development of these days must have been is in part indicated by the very language and vocabulary of the period. The commonest utterances of the commonest citizens in the time of the Colour Revolt seem to have been suffused with a richer tinge of word or thought; and to that era we are even now indebted for our finest poetry and for whatever rhythm still remains in the more scientific utterance of these modern days.

1 Although Abbott does not say so, color can be viewed as an extra dimension (or dimensions). Imagine, for instance, that an object’s color can change continuously from red through purple to blue. Then, in addition to locating the position of that object in space (which requires two dimensions in Flatland and three in Spaceland), it is also necessary to locate the color of that object—which can be considered as a position in a “color space” running in the red-blue “direction”; see Flatterland chapter 4, “A Hundred and One Dimensions.” There is no question that in this setting, color is independent of spatial location and can thus be considered an extra dimension. The idea is not new. In his 1927 The Philosophy of Space and Time, Hans Reichenbach says,

Let us assume that the three dimensions of space are visualized in the customary fashion, and let us substitute a color for the fourth dimension. Every physical object is liable to changes in color as well as in position. An object might, for example, be capable of going through all shades from red through violet to blue. A physical interaction between any two bodies is possible only if they are close to each other in space as well as in color. Bodies of different colors would penetrate each other without interference. . . . If we lock a number of [red] flies into a red glass globe, they may yet escape: they may change their color to blue and are then able to penetrate the red globe.

Artists have long located the colors perceived by the human eye in a two-dimensional “color triangle” whose vertices are “primary” colors and whose interior points are mixtures of these. The traditional primary colors are red, yellow, and blue, but we’ll shortly see that other choices are more appropriate. In modern times, such concepts are vital to the computer graphics industry. Computer screen colors combine additively—the effect of a mixture depends on the sum of the component colors because the pixels (tiny fluorescent dots) that make up the screen emit light. The RGB color triangle for additive colors has vertices at Red, Green, and Blue. Combining blue plus red (in equal amounts) gives magenta, red and green give yellow, and green and blue give cyan. All three together give white. Paints and inks, however, combine subtractively—the effect of a mixture depends on the differences between the component colors because paints absorb light (of all colors that differ from the one we see). The CMYK model employs Cyan, Magenta, and Yellow as its primary colors. A mixture of all three should in principle give black, but in practice the result is a muddy brown, so black (K) is added explicitly as a fourth component. Now a mixture of cyan and magenta gives blue, magenta and yellow give red, and yellow and cyan give green. The picture on your computer screen is created using the RGB system, but when you print it, your inkjet printer uses the CMYK system. This is one reason why digital photographs can look different on paper and on screen.

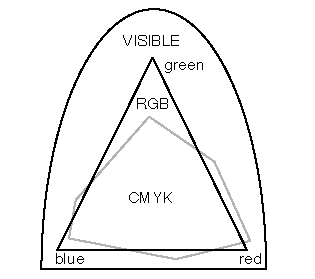
Figure 24 Color gamuts of RGB, CMYK, and visible light.

The issues here are complex, for some colors, such as brown, fall outside the standard color triangle. The gamut of a system is the range of colors it can produce. The CMYK gamut is smaller than the RGB gamut, which in turn is smaller than the full gamut of colors visible to the human eye (Figure 24). Other factors, such as brightness, introduce yet further dimensions into color vision. These extra dimensions are just as real as the traditional spatial dimensions. Indeed, the architecture of the visual system in the human brain is extremely complex because it has to take into account the additional dimensions of color and brightness. Reichenbach chooses a one-dimensional subspace (red-violet-blue) of the two-dimensional color triangle to illustrate a fourth dimension. If he had chosen the entire spectrum of colors, he would have been visualizing a five-dimensional space.

2 Here the first edition has “. . . threw a transient charm upon . . .”

3 This sentence is largely a play on words, and its mathematical meaning is delicate. Abbott discusses coloring polygons on the unstated assumption that each “side” (meaning “edge”) gets a single color. There is, of course, no necessity to do this: The Flatland equivalent of stripes, or variegation, is straightforward. However, he is trying to set up a key narrative point: the dangerous equivalence of Women and Priests. To do this, he attempts to use a play on words to establish in the reader’s mind that both Women and Priests have no sides. A side of a polygon is a straight line segment, and a Flatland Woman is a single straight line segment—hence “one side,” hence (with a pointed remark about plurals) no sides. Similarly, a circle has a curved circumference, also “no sides.” However, a line segment actually has two sides (left and right, so to speak), so—provided that the paint can be attached to the surface rather than pervading the whole line like a dye—Women could be painted with two colors. Indeed, a two-sided polygon (2-gon or digon) is a line segment described twice, which would be consistent with two distinct colors.

4 The wordplay here works only if the Circles— n-gons for very large n—can be considered true circles. Strictly speaking, this is not the case, but it would be a shame to let mere facts spoil a fantasy story, so Abbott slides neatly over the difficulty. In conventional mathematics, a circle is the limit of a sequence of n-gons as n tends to infinity, but it is not itself a polygon.

5 Here Abbott makes a rare slip, for such a sight could never be seen in the Flatland fog. Admittedly, the fog “prevails during the greater part of the year in all parts save the torrid zones” and so might not be present during this particular spectacle, but such spectacles must have been common because Abbott tells us that “How great and glorious the sensuous development of these days must have been is in part indicated by the very language and vocabulary of the period.” Rare spectacles would not have had such a marked influence on day-today language.