§ 15.—Concerning a Stranger from Spaceland.
FROM DREAMS I proceed to facts.
It was the last day of the 1999th year of our era. The pattering of the rain had long ago announced nightfall; and I was sitting1 in the company of my wife, musing on the events of the past and the prospects of the coming year, the coming century, the coming Millennium.
My four Sons and two orphan Grandchildren had retired to their several apartments; and my wife alone remained with me to see the old Millennium out and the new one in.
I was rapt in thought, pondering in my mind some words that had casually issued from the mouth of my youngest Grandson, a most promising young Hexagon of unusual brilliancy and perfect angularity. His uncles and I had been giving him his usual practical lesson in Sight Recognition, turning ourselves upon our centres, now rapidly, now more slowly, and questioning him as to our positions; and his answers had been so satisfactory that I had been induced to reward him by giving him a few hints on Arithmetic, as applied to Geometry.
Taking nine Squares,2 each an inch every way, I had put them together so as to make one large Square, with a side of three inches, and I had hence proved to my little Grandson that—though it was impossible for us to see the inside of the Square—yet we might ascertain the number of square inches in a Square by simply squaring the number of inches in the side: “and thus,” said I, “we know that 32, or 9, represents the number of square inches in a Square whose side is 3 inches long.”
The little Hexagon meditated on this a while and then said to me; “But you have been teaching me to raise numbers to the third power:3 I suppose 33 must mean something in Geometry; what does it mean?” “Nothing at all,” replied I, “not at least in Geometry; for Geometry has only Two Dimensions.” And then I began to shew the boy how a Point by moving through a length of three inches makes a Line of three inches, which may be represented by 3; and how a Line of three inches, moving parallel to itself through a length of three inches, makes a Square of three inches every way, which may be represented by 32.
Upon this, my Grandson, again returning to his former suggestion, took me up rather suddenly and exclaimed, “Well, then, if a Point by moving three inches, makes a Line of three inches represented by 3; and if a straight Line of three inches, moving parallel to itself, makes a Square of three inches every way, represented by 32; it must be that a Square of three inches every way, moving somehow parallel to itself (but I don’t see how) must make Something else (but I don’t see what) of three inches every way—and this must be represented by 33.”
“Go to bed,” said I, a little ruffled by this interruption: “if you would talk less nonsense, you would remember more sense.”
So my Grandson had disappeared in disgrace; and there I sat by my Wife’s side, endeavouring to form a retrospect of the year 1999 and of the possibilities of the year 2000, but not quite able to shake off the thoughts suggested by the prattle of my bright little Hexagon. Only a few sands now remained in the half-hour glass. Rousing myself from my reverie I turned the glass Northward for the last time in the old Millennium; and in the act, I exclaimed aloud, “The boy is a fool.”
Straightway I became conscious of a Presence in the room, and a chilling breath thrilled through my very being. “He is no such thing,” cried my Wife, “and you are breaking the Commandments in thus dishonouring your own Grandson.” But I took no notice of her. Looking round in every direction I could see nothing; yet still I felt a Presence, and shivered as the cold whisper came again. I started up. “What is the matter?” said my Wife, “there is no draught; what are you looking for? There is nothing.” There was nothing; and I resumed my seat, again exclaiming, “The boy is a fool, I say; 33 can have no meaning in Geometry.” At once there came a distinctly audible reply, “The boy is not a fool; and 33 has an obvious Geometrical meaning.”
My Wife as well as myself heard the words, although she did not understand their meaning, and both of us sprang forward in the direction of the sound. What was our horror when we saw before us a Figure! At the first glance it appeared to be a Woman, seen sideways; but a moment’s observation shewed me that the extremities passed into dimness too rapidly to represent one of the Female Sex; and I should have thought it a Circle,4 only that it seemed to change its size in a manner impossible for a Circle or for any regular Figure of which I had had experience.
But my Wife had not my experience, nor the coolness necessary to note these characteristics. With the usual hastiness and unreasoning jealousy of her Sex, she flew at once to the conclusion that a Woman had entered the house through some small aperture. “How comes this person here?” she exclaimed, “you promised me, my dear, that there should be no ventilators in our new house.” “Nor are there any,” said I; “but what makes you think that the stranger is a Woman? I see by my power of Sight Recognition——”“Oh, I have no patience with your Sight Recognition,” replied she, “‘Feeling is believing’ and ‘A Straight Line to the touch is worth a Circle to the sight’”—two Proverbs, very common with the Frailer Sex in Flatland.
“Well,” said I, for I was afraid of irritating her, “if it must be so, demand an introduction.” Assuming her most gracious manner, my Wife advanced towards the Stranger, “Permit me, Madam, to feel and be felt by——” then, suddenly recoiling, “Oh! it is not a Woman, and there are no angles either, not a trace of one. Can it be that I have so misbehaved to a perfect Circle?”
“I am indeed, in a certain sense a Circle,” replied the Voice, “and a more perfect Circle than any in Flatland; but to speak more accurately, I am many Circles in one.” Then he added more mildly, “I have a message, dear Madam, to your husband, which I must not deliver in your presence; and, if you would suffer us to retire for a few minutes——” But my Wife would not listen to the proposal that our august Visitor should so incommode himself, and assuring the Circle that the hour of her own retirement had long passed, with many reiterated apologies for her recent indiscretion, she at last retreated to her apartment.
I glanced at the half-hour glass. The last sands had fallen. The third Millennium had begun. 5
1 The first edition has “. . . you in Flatland . . . ,” an evident slip.
2 If three lines of length 1 inch (I use inches here because Abbott does and omit metric equivalents) are joined end to end, the result is a line of length 3 inches, the same shape as the original line but three times as large (Figure 27a). However, a square cannot be made three times as large by joining together three copies: Instead, it takes nine such copies (Figure 27b). Note that 9 is the square of 3—that is, 9 = 32 = 3 x 3. And the power 2 here is the dimension of a square.
In “What Is the Fourth Dimension?” C. H. Hinton uses a similar argument, only there he uses powers of 2 rather than 3. “Casting Out the Self,” from his first volume of Scientific Romances, has a long discussion of a 3 x 3 x 3 cube.
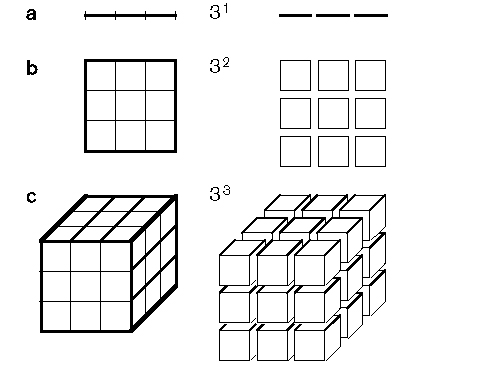
Figure 27 How figures of different dimensions scale: (a) line; (b) square; (c) cube.
3 Arithmetically, there is no difficulty in extending the notion of “square” to higher powers:
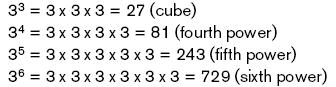
and so on. To us the cube has a clear geometric meaning (as the term suggests). To wit, if 27 unit cubes are stacked together in the right way (Figure 27c), then they form a cube three times the size. And here the power 3 is the dimension of the cube.
A. Square’s bright little hexagonal grandson is convinced that because 33 has an algebraic meaning, it must also have a geometric one, but grandfather (at this stage of the narrative) disagrees. In the same way, a Victorian reader would disagree that 34 has a geometric meaning. The ancient Greek geometers had a similar attitude. They used not raw numbers but magnitudes, numbers with units—specifically, lengths of lines. The product of two numbers was thus an area, that of three was a volume, and that of four was . . . they didn’t say. They rather slid over the problem and felt uncomfortable when more than three magnitudes were multiplied together. However, such a multiplication occurs in a famous (and useful) theorem, Heron’s Formula for the area of a triangle. If the sides of the triangle are a, b, and c, and we define the semiperimeter s = (a + b + c)/2, then the area is the square root of s(s - a)(s - b)(s - c). The formula thus involves the product of four lengths. One way out of the dilemma (which seems not to have occurred to the Greeks) is to rewrite this as the square root of s(s - a) multiplied by the square root of (s - b)(s - c). Each of these products involves just two numbers, and the square roots reduce them from areas to lengths, so the theorem expresses the area of the triangle as a product of two lengths, with no interpretational difficulties.
Related ideas have been extended to more exotic shapes, such as the Sierpinski gasket (Figure 28) invented by the Polish mathematician Waclaw Sier-pinski (1882–1969). If k copies of a shape can be joined together to make an exact copy that is b times as big, then the similarity dimension of the shape is

where log is the natural logarithm. For a cube, k = 27 and b = 3, and
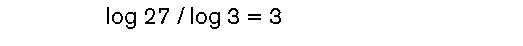
as expected. For the Sierpinski gasket, k = 3 and b = 2, and
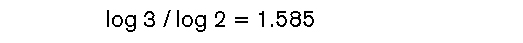
which is not a whole number. Similarity dimension, unlike “number of directions,” need not take whole-number values. The Sierpinski gasket is an example of a fractal, a geometric shape with fine structure on all scales of magnification (see Benoit Mandelbrot, The Fractal Geometry of Nature; and chapter 5 of Flatterland, “One and a Quarter Dimensions”). The similarity dimension has a profound generalization, the Hausdorff–Besicovitch or fractal dimension (see Kenneth Falconer, Fractal Geometry).

Figure 28 The Sierpinski gasket. The figure shows an early stage; the process of subdividing triangles should be continued indefinitely.
4 When a sphere intersects a plane, the result is a circle. As the sphere moves relative to the plane, the circle changes size; observe that (page 143) Abbott draws the intersections as having sharp ends when actually they are ellipses—circles viewed in perspective. Conversely, a high-dimensional shape can be visualized by intersecting it with a lower-dimensional space and moving the shape relative to that space to create a series of “cross sections.” In this manner, mathematicians can visualize four-dimensional forms as sequences of three-dimensional slices, five-dimensional forms as two-dimensional arrays of three-dimensional slices, and so on. This technique can be traced way back into mathematical folklore. One person who made it explicit, and placed great store by it, was C. H. Hinton. The story involves a curious and complicated series of influences and relationships that revolved around Alicia Stott (née Boole), third daughter of the English mathematician George Boole (1815–1864). There seems to be a strong historical link among Hinton’s four-dimensional speculations, some brilliant mathematical discoveries of Alicia’s own, and Abbott’s writing of Flatland.
George Boole is best known for Boolean algebra, a form of symbolic logic in which 1 represents “true,” 0 represents “false,” and the logical operations not, and, and or are formulated algebraically. It is widely used today as a basis for computer science. It also gave a big boost to the development of mathematical logic and eventually led to deep and important work on the foundations of mathematics. This includes the epic theorems of Kurt Gödel (1906–1978), who proved that the logical consistency of arithmetic can never be proved and that some statements in arithmetic are undecidable— neither provable nor disprovable. Boole, the son of a Lincoln shoemaker, was a child prodigy, but his education came to an abrupt halt when he was sixteen because of the family’s financial circumstances. His two books The Mathematical Analysis of Logic (1847) and An Investigation of the Laws of Thought (1854) laid the foundations of theoretical computer science. (Lewis Carroll was also interested in mathematical logic and published Symbolic Logic I in 1896. There is no second volume.) Boole also worked on the theory of invariants, differential equations, and probability. In 1849 he was appointed first professor of mathematics in Ireland’s new Queen’s College, now University College, Cork.
In 1855 he married Mary Everest (1832–1916), daughter of the Reverend Thomas Roupell Everest, Rector of Wickwar, Gloucestershire. Her uncle was Lieutenant Colonel Sir George Everest (1790–1866), after whom the world’s highest mountain is named. Mary showed an early aptitude for mathematics, though in later life her knowledge of the subject seems poor. In 1852 Boole visited the Everest family and began giving Mary lessons in mathematics; their relationship grew from there, although Boole considered himself too old to marry. His mind changed abruptly when Mary’s father died in 1855, leaving her destitute: Boole immediately proposed. Mary was for a time secretary to James Hinton, a former friend of her father’s, who was an ear surgeon, an enthusiastic advocate of sexual freedom, and C. H. Hinton’s father. Mary promoted the elder Hinton’s ideas; she was a prolific writer of extremely uneven quality, and her work ranges from the insightful to the bizarre. She also tried to promote her husband’s investigations in logic, with dire results.
The Booles had five daughters: Mary Ellen (1856–?), Margaret (1858–?), Alicia (1860–1940), Lucy Everest (1862–1905), and Ethel Lilian (1864– 1960). Mary Ellen married C. H. Hinton. Three of Hinton’s books are important here: A New Era of Thought (1884), The Fourth Dimension (1904), and An Episode of Flatland (1907). In the first two of these, Hinton developed a way to visualize four-dimensional solids as a series of three-dimensional cross sections. He used a set of 81 (= 34) tiny wooden cubes, colored and labeled in a highly ingenious manner, to aid his thoughts. (Earlier, he had assigned a two-word Latin name to each of the 46,656 (= 363) 1-inch subcubes of a cube whose side was 1 yard—36 inches.) According to McHale, “. . . it is quite probable that [Hinton’s] interest in these topics was stimulated by his mother-in-law Mary Boole and her daughters.” An Episode of Flatland is not set on Abbott’s Flatland; it is Hinton’s Flatlandesque tale of Astria. As we have already mentioned, Hinton wrote several articles about two-dimensional worlds in the early 1880s, and Ban-choff has suggested that “. . . it is likely that Abbott could have seen one or more of [Hinton’s] articles before he wrote Flatland.” Another connection should be noted: Mary Boole (senior) was a friend of Herbert George Wells (1866–1946), and there is a fictional character named Boole in his The New Machiavelli (1911). Wells’s The Time Machine (1895) takes its scientific inspiration from the geometry of the fourth dimension, and it seems that Wells was influenced in this by Hinton.
The second Boole daughter, Margaret, married the artist Edward Ingram Taylor. Their son Geoffrey Ingram Taylor became one of the leading applied mathematicians of the twentieth century: He worked on (among other topics) fluid mechanics, shock waves, meteorology, icebergs, crystals, and aeronautics.
It is the third daughter, Alicia (generally known as Alice), who provides the strongest mathematical link to Flatland—not by influencing its writing but by developing Hinton’s ideas, upon which it seems clear that Flatland was based, into serious mathematics. Alicia possessed remarkable innate mathematical talents (her father died when she was four, so his possible influence as a teacher can be ruled out). At a time when women were actively discouraged from taking up mathematics, Alice studied Euclid. At the age of eighteen she became entranced by C. H. Hinton’s tiny wooden cubes. She failed to share his fascination with the mystical aspects of the fourth dimension but found its geometry fascinating. She developed Hinton’s methods (series of three-dimensional sections) and introduced the name polytope for a multidimensional solid. By purely geometric reasoning, she discovered that there are exactly six regular four-dimensional poly-topes, formed from 5, 16, or 600 tetrahedra, 8 cubes, 24 octahedra, or 120 dodecahedra. She built beautiful cardboard models of their three-dimensional sections but then abandoned mathematics in 1890 to marry Walter Stott. The story might have ended there, but around 1900 she came across a paper by Peiter Hendrik Schoute (1846–1923) of Gronin-gen University, who had obtained exactly the same results by purely analytic methods. Schoute encouraged her to publish her work, which she did in 1900 and 1910, and they collaborated until his death in 1913. In 1930 her nephew G. I. Taylor introduced her to the geometer H(arold) S(cott) M(acdonald) Coxeter (1907– ), who rekindled her interest in fourdimensional polytopes and described her work in his Regular Polytopes (1948, 2nd ed. 1963).
Lucy, the fourth daughter, did not marry and died young. She learned chemistry to get a job in a chemist’s shop and went on to become a fellow of the Institute of Chemistry and (it is believed) the first woman professor of chemistry at the Royal Free Hospital, London.
Perhaps the most remarkable of the Boole daughters was the last: Ethel Lilian (known as Lily in her youth). Around 1885 she met Sergei Kravchinski (pseudonym Stepniak), who had assassinated General N.V. Mezentsov. The general was Gendarme Chief and 3rd Section Head Controller; the 3rd Section was the Tsarist Secret Police. Kravchinski stabbed him in the stomach on a busy street, leaped into a passing droshky (open horse-drawn carriage), and fled Russia. Under Kravchinski’s influence, Ethel Lilian became a political activist for the Society of Friends of Russian Freedom, a Marxist organization. In 1891 she married a Lithuanian refugee, Wilfred Michail Voynich (1865–1930) and embarked on a career as a writer. Her first book, Stories from Garshin (1893), was a translation of a book by Stepniak; she wrote many others, including the novel The Gadfly (1897), which is about a devout young man who loses his faith and is maimed, mutilated, and tortured to death. It was a wild success, especially in Russia, and other novels followed. In 1912 her husband bought a curious document, the “Voynich manuscript,” which was written in code—some say by Roger Bacon (c.1220–1292). In 1960 it was sold for $160,000, and it is now in the vaults of Yale University. Despite intense efforts, it has not been deciphered. Cryptographic expert David Kahn called it “the most mysterious manuscript in the world.”
The important aspect of this strange web of family influences is that it connects Flatland, albeit indirectly, to the mainstream mathematics of Abbott’s day by way of a seminal figure in English mathematics: George Boole. It gives us a feeling for the Victorian social and scientific undercurrents out of which Flatland emerged. The lives and work of Boole’s five astonishing daughters add grace notes to this curious web of interconnections. And we will shortly see that Wells, a family friend of the Booles, is linked to Hinton and Abbott in another way, through his interest in the fourth dimension. The story of Boole, his family, and its influences is told in graphic detail by Desmond MacHale in his superb biography George Boole, His Life and Work (1985).
5 The first edition of Flatland has “second Millennium,” which is wrong. So does at least one modern edition, the Shambhala one.
1 When I say “sitting,” of course I do not mean any change of attitude such as you in Spaceland1 signify by that word; for as we have no feet, we can no more “sit” nor “stand” (in your sense of the word) than one of your soles or flounders.
Nevertheless, we perfectly well recognize the different mental states of volition implied in “lying,” “sitting,” and “standing,” which are to some extent indicated to a beholder by a slight increase of lustre corresponding to the increase of volition.
But on this, and a thousand other kindred subjects, time forbids me to dwell.