§ 16.—How the Stranger vainly endeavoured to reveal to me in words the mysteries of Spaceland.

AS SOON AS the sound of the Peace-cry of my departing Wife had died away, I began to approach the Stranger with the intention of taking a nearer view and of bidding him be seated: but his appearance struck me dumb and motionless with astonishment. Without the slightest symptoms of angularity he nevertheless varied every instant with gradations of size and brightness scarcely possible for any Figure within the scope of my experience. The thought flashed across me that I might have before me a burglar or cut-throat, some monstrous Irregular Isosceles, who, by feigning the voice of a Circle, had obtained admission somehow into the house, and was now preparing to stab me with his acute angle.

In a sitting-room, the absence of Fog (and the season happened to be remarkably dry), made it difficult for me to trust to Sight Recognition, especially at the short distance at which I was standing. Desperate with fear, I rushed forward with an unceremonious, “You must permit me, Sir—” and felt him. My Wife was right. There was not the trace of an angle, not the slightest roughness or inequality: never in my life had I met with a more perfect Circle. He remained motionless while I walked round him, beginning from his eye and returning to it again. Circular he was throughout, a perfectly satisfactory Circle; there could not be a doubt of it. Then followed a dialogue, which I will endeavour to set down as near as I can recollect it, omitting only some of my profuse apologies—for I was covered with shame and humiliation that I, a Square, should have been guilty of the impertinence of feeling a Circle. It was commenced by the Stranger with some impatience at the lengthiness of my introductory process.

Stranger. Have you felt me enough by this time? Are you not introduced to me yet?

I. Most illustrious Sir, excuse my awkwardness, which arises not from ignorance of the usages of polite society, but from a little surprise and nervousness, consequent on this somewhat unexpected visit. And I beseech you to reveal my indiscretion to no one, and especially not to my Wife. But before your Lordship enters into further communications, would he deign to satisfy the curiosity of one who would gladly know whence his Visitor came?

Stranger. From Space, from Space, Sir: whence else?

I. Pardon me, my Lord, but is not your Lordship already in Space, your Lordship and his humble servant, even at this moment?

Stranger. Pooh! what do you know of Space? Define Space.

I. Space, my Lord, is height and breadth indefinitely prolonged.

Stranger. Exactly: you see you do not even know what Space is. You think it is of Two Dimensions only; but I have come to announce to you a Third —height, breadth, and length.

I. Your Lordship is pleased to be merry.We also speak of length and height, or breadth and thickness, thus denoting Two Dimensions by four names. Stranger. But I mean not only three names, but Three Dimensions.

I. Would your Lordship indicate or explain to me in what direction is the Third Dimension,1 unknown to me?

Stranger. I came from it. It is up above and down below.

I. My Lord means seemingly that it is Northward and Southward.

Stranger. I mean nothing of the kind. I mean a direction in which you cannot look, because you have no eye in your side.

I. Pardon me, my Lord, a moment’s inspection will convince your Lordship that I have a perfect luminary at the juncture of two of my sides.

Stranger. Yes: but in order to see into Space you ought to have an eye, not on your Perimeter, but on your side, that is, on what you would probably call your inside; but we in Spaceland should call it your side.

I. An eye in my inside! An eye in my stomach!2 Your Lordship jests.

Stranger. I am in no jesting humour. I tell you that I come from Space, or, since you will not understand what Space means, from the Land of Three Dimensions whence I but lately looked down upon your Plane which you call Space forsooth. From that position of advantage I discerned all that you speak of as solid (by which you mean “enclosed on four sides”), your houses, your churches, your very chests and safes, yes even your insides and stomachs, all lying open and exposed to my view.

I. Such assertions are easily made, my Lord.

Stranger. But not easily proved, you mean. But I mean to prove mine.

When I descended here, I saw your four Sons, the Pentagons, each in his apartment, and your two Grandsons the Hexagons; I saw your youngest Hexagon remain a while with you and then retire to his room, leaving you and your Wife alone. I saw your Isosceles servants, three in number, in the kitchen at supper, and the little Page in the scullery. Then I came here, and how do you think I came?

I. Through the roof, I suppose.

Stranger. Not so. Your roof, as you know very well, has been recently repaired, and has no aperture by which even a Woman could penetrate. I tell you I come from Space. Are you not convinced by what I have told you of your children and household?

I. Your Lordship must be aware that such facts touching the belongings of his humble servant might be easily ascertained by any one in the neighbourhood possessing your Lordship’s ample means of obtaining information.

Stranger. (To himself. ) What must I do?³ Stay; one more argument suggests itself to me. When you see a Straight Line—your wife, for example— how many Dimensions do you attribute to her?

I. Your Lordship would treat me as if I were one of the vulgar who, being ignorant of Mathematics, suppose that a Woman is really a Straight Line, and only of One Dimension. No, no, my Lord; we Squares are better advised, and are as well aware as your Lordship that a Woman, though popularly called a Straight Line, is, really and scientifically, a very thin Parallelogram,⁴ possessing Two Dimensions, like the rest of us, viz., length and breadth (or thickness).

Stranger. But the very fact that a Line is visible implies that it possesses yet another Dimension.

I. My Lord, I have just acknowledged that a Woman is broad as well as long. We see her length, we infer her breadth; which, though very slight, is capable of measurement.

Stranger. You do not understand me. I mean that when you see a Woman, you ought—besides inferring her breadth—to see her length, and to see what we call her height; although that last Dimension is infinitesimal in your country.⁵ If a Line were mere length without “height,” it would cease to occupy Space and would become invisible. Surely you must recognize this?

I. I must indeed confess that I do not in the least understand your Lordship. When we in Flatland see a Line, we see length and brightness. If the brightness disappears, the Line is extinguished, and, as you say, ceases to occupy Space. But am I to suppose that your Lordship gives to brightness the title of a Dimension,6 and that what we call “bright” you call “high”?

Stranger. No, indeed. By “height” I mean a Dimension like your length: only, with you, “height” is not so easily perceptible, being extremely small.⁷

I. My Lord, your assertion is easily put to the test. You say I have a Third Dimension, which you call “height.” Now, Dimension implies direction and measurement. Do but measure my “height,” or merely indicate to me the direction in which my “height” extends, and I will become your convert. Otherwise, your Lordship’s own understanding must hold me excused.

Stranger. (To himself. ) I can do neither. How shall I convince him? Surely a plain statement of facts followed by ocular demonstration ought to suffice. —Now, Sir; listen to me.

You are living on a Plane. What you style Flatland is the vast level surface of what I may call a fluid,⁸ on, or in, the top of which you and your countrymen move about, without rising above it or falling below it.

I am not a plane Figure, but a Solid. You call me a Circle; but in reality I am not a Circle, but an infinite number of Circles, of size varying from a Point to a Circle of thirteen inches in diameter, one placed on the top of the other. When I cut through your plane as I am now doing, I make in your plane a section which you, very rightly, call a Circle. For even a Sphere—which is my proper name in my own country—if he manifest himself at all to an inhabitant of Flatland—must needs manifest himself as a Circle.

Do you not remember—for I, who see all things, discerned last night the phantasmal vision of Lineland written upon your brain—do you not remember, I say, how, when you entered the realm of Lineland, you were compelled to manifest yourself to the King, not as a Square, but as a Line, because that Linear Realm had not Dimensions enough to represent the whole of you, but only a slice or section of you? In precisely the same way, your country of Two Dimensions is not spacious enough to represent me, a being of Three, but can only exhibit a slice or section⁹ of me, which is what you call a Circle.

The diminished brightness of your eye indicates incredulity. But now prepare to receive proof positive of the truth of my assertions. You cannot indeed see more than one of my sections, or Circles, at a time; for you have no power to raise your eye out of the plane of Flatland; but you can at least see that, as I rise in Space, so my sections become smaller. See now, I will rise; and the effect upon your eye will be that my Circle will become smaller and smaller till it dwindles to a point and finally vanishes.

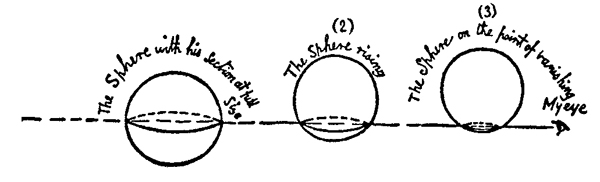
There was no “rising” that I could see;¹⁰ but he diminished and finally vanished. I winked once or twice to make sure that I was not dreaming. But it was no dream. For from the depths of nowhere came forth a hollow voice¹¹—close to my heart it seemed—“Am I quite gone? Are you convinced now? Well, now I will gradually return to Flatland and you shall see my section become larger and larger.”

Every reader in Spaceland will easily understand that my mysterious Guest was speaking the language of truth and even of simplicity. But to me, proficient though I was in Flatland Mathematics, it was by no means a simple matter. The rough diagram given above will make it clear to any Spaceland child that the Sphere, ascending in the three positions indicated there, must needs have manifested himself to me, or to any Flat-lander, as a Circle, at first of full size, then small, and at last very small indeed, approaching to a Point. But to me, although I saw the facts before me, the causes were as dark as ever. All that I could comprehend was, that the Circle had made himself smaller and vanished, and that he had now reappeared and was rapidly making himself larger.

When he regained his original size, he heaved a deep sigh; for he perceived by my silence that I had altogether failed to comprehend him.¹² And indeed I was now inclining to the belief that he must be no Circle at all, but some extremely clever juggler; or else that the old wives’ tales were true, and that after all there were such people as Enchanters and Magicians.

After a long pause he muttered to himself, “One resource alone remains, if I am not to resort to action. I must try the method of Analogy.” Then followed a still longer silence, after which he continued our dialogue.

Sphere. Tell me,Mr. Mathematician;¹³ if a Point moves Northward, and leaves a luminous wake, what name would you give to the wake?

I. A straight Line.

Sphere. And a straight Line has how many extremities?

I. Two.

Sphere. Now conceive the Northward straight Line moving parallel to itself, East and West, so that every point in it leaves behind it the wake of a straight Line. What name will you give to the Figure thereby formed? We will suppose that it moves through a distance equal to the original straight Line.—What name, I say?

I. A Square.

Sphere. And how many sides has a Square? How many angles?

I. Four sides and four angles.

Sphere. Now stretch your imagination a little, and conceive a Square in Flatland, moving parallel to itself upward.

I. What? Northward?

Sphere. No, not Northward; upward; out of Flatland altogether.

If it moved Northward, the Southern points in the Square would have to move through the positions previously occupied by the Northern points. But that is not my meaning.

I mean that every Point in you—for you are a Square and will serve the purpose of my illustration— every Point in you, that is to say in what you call your inside, is to pass upwards through Space in such a way that no Point shall pass through the position previously occupied by any other Point; but each Point shall describe a straight Line of its own. This is all in accordance with Analogy; surely it must be clear to you.

Restraining my impatience—for I was now under a strong temptation to rush blindly at my Visitor and to precipitate him into Space, or out of Flatland, anywhere, so that I could get rid of him—I replied:—

“And what may be the nature of the Figure which I am to shape out by this motion which you are pleased to denote by the word ‘upward’? I presume it is describable in the language of Flatland.”

Sphere. Oh, certainly. It is all plain and simple, and in strict accordance with Analogy—only, by the way, you must not speak of the result as being a Figure, but as a Solid. But I will describe it to you. Or rather not I, but Analogy.

We began with a single Point, which of course —being itself a Point—has only one terminal Point.

One Point produces a Line with two terminal Points.

One Line produces a Square with four terminal Points.

Now you can give yourself the answer to your own question: 1, 2, 4, are evidently in Geometrical Progression. What is the next number?

I. Eight.

Sphere. Exactly. The one Square produces a Something-which-you-do-not-as-yet-know-a-name-for-but which-we-call-a-Cube with eight terminal Points.Now are you convinced?

I. And has this Creature sides, as well as angles or what you call “terminal Points”?

Sphere. Of course; and all according to Analogy. But, by the way, not what you call sides, but what we call sides. You would call them solids.

I. And how many solids or sides will appertain to this Being whom I am to generate by the motion of my inside in an “upward” direction, and whom you call a Cube?

Sphere. How can you ask? And you a mathematician! The side of anything is always, if I may so say, one Dimension behind the thing. Consequently, as there is no Dimension behind a Point, a Point has 0 sides; a Line, if I may so say, has 2 sides (for the Points of a Line may be called by courtesy, its sides); a Square has 4 sides; 0, 2, 4; what Progression do you call that?

I. Arithmetical.

Sphere. And what is the next number?

I. Six.

Sphere. Exactly. Then you see you have answered your own question. The Cube which you will generate will be bounded by six sides, that is to say, six of your insides. You see it all now, eh?

“Monster,” I shrieked, “be thou juggler, enchanter, dream, or devil, no more will I endure thy mockeries. Either thou or I must perish.” And saying these words I precipitated myself upon him.

1 A. Square is now experiencing the same difficulty that the King of Lineland faced in his dream.

2 Abbott has a lot of fun with a curious feature of dimensionality. To the creatures of Flatland, confined to their plane, the interior of a Polygon is not directly visible because its edges get in the way. If the plane is viewed from a third dimension, the entire interior, including internal organs, becomes visible. However, A. Square does not just need an eye in his stomach: It has to be pointing out of his universe. It would be equally effective (and equally impossible) for him to point his existing eye in that direction. By analogy, if our three-dimensional world could be viewed by a creature from a fourth dimension, our own insides would be completely visible to that creature.

The bizarre phenomena that could easily be exploited by a being from the fourth dimension have long intrigued philosophers. Rudy Rucker refers to these collectively as hyperspace philosophers—the word hyperspace is often used for four-dimensional space (sometimes higher). One of the earliest hyper-space philosophers was Henry More (1614–1687), who disliked the idea of angels and spirits as disembodied, insubstantial beings; he argued that if they actually existed, they must take up space. However, there is a problem in fitting a spatially extended soul into a physical body: Where do you put it, and why hasn’t medical science located it? All is solved if the spirit world is four-dimensional, a concept that, in his Enchiridion Metaphysicum of 1671, More called spissitude—a kind of “Extra-Height,” in A. Square’s terminology, or a slight thickening along a fourth dimension. Living bodies have more spissitude than dead ones. In 1747 Immanuel Kant (1724–1804) wrote,

A science of all these possible kinds of space [with more than three dimensions] would undoubtably be the highest enterprise which a finite understanding could undertake in the field of geometry. . . . If it is possible that there are extensions with other dimensions, it is also very probable that God has somewhere brought them into being: for His works have all the magnitude and manifoldness of which they are capable.

Cranks and eccentrics also found the concept of a fourth dimension fascinating, invoking it to explain the “spirit world” of the spiritualist movement. Four-dimensional space provides a place for the dead to continue existing, alongside our universe (and hence able to communicate with it) but not in our universe. A prominent advocate of this kind of mysticism was Peter Demianovich Ouspensky (1878–1947), who revealed the mysteries of the fourth dimension to the intellectuals of Tsarist Russia. Ouspensky was a disciple of George Ivanovitch Gurdjieff (1872–1949), once described in Time magazine as “a remarkable blend of P.T. Barnum, Rasputin, Freud, Groucho Marx, and everybody’s grandfather.” In his 1908 The Fourth Dimension, Ouspensky writes,

If the fourth dimension exists while we possess only three, it means that we have no real existence, that we exist only in somebody’s imagination and that all our thoughts, feelings and experiences take place in the mind of some other higher being . . . the whole of our universe is but an artificial world created by his fantasy.

If we do not want to agree with this we must recognize ourselves as beings in four dimensions. . . . [W]e have no need to think that the spirits that appear or fail to appear at spiritualistic seances must be the only possible beings of four dimensions. We may have very good reason for saying that we are ourselves beings of four dimensions and we are turned towards the third dimension with only one of our sides, i.e., with only a small part of our being.

His Tertium Organum of 1912 adds,

When we shall see or feel ourselves in the world of four dimensions we shall see that the world of three dimensions does not really exist and has never existed; that it was the creation of our own fantasy, a phantom host, an optical illusion, a delusion—anything one pleases excepting only reality.

Ouspensky’s influence shows up, very briefly, in Book 5, Section 3 of the 1879–1880 novel The Brothers Karamazov by Fyodor Dostoyevsky (1821– 1881), in a passage where Ivan Karamazov pursues possible connections between high-dimensional and non-Euclidean geometries and the existence of God:

. . . if God exists and if he really did create the earth then, as common knowledge tells us, he created it according to Euclidean geometry, while he created the human mind with an awareness of only three spatial dimensions. Even so, there have been and still are even today geometers and philosophers of the most remarkable kind who doubt that the entire universe or, even more broadly, the entirety of being was created solely according to Euclidean geometry.

Vladimir Ilich Lenin (1870–1924) was sufficiently worried by this sort of thing that in 1908 he wrote Materialism and Empirio-Criticism, attacking the idea of spirits in four-dimensional space. Mathematics, said Lenin, may open up the possibility of space of four dimensions, but only in three-dimensional space can political revolution occur.

3 This begins one of the two new passages that Abbott mentions in his preface to the second edition. The insertion continues until “Stranger. (To Himself.) I can do neither?” on page 141. In place of this new passage, the first edition has: “Stranger. How shall I convince him?”

4 Abbott is setting the reader up for the Stranger’s subsequent argument that everything in Flatland really possesses a third dimension but is very “thin” in that direction. Otherwise, the Stranger argues, Women would be invisible in Flatland. Abbott’s reasoning here seems confused. In a three-dimensional world—space—light is confined to the space and is scattered by surfaces. The brightness of an object is determined by how much light it scatters per unit area. Analogously, in a two-dimensional world —a plane—light is confined to the plane and is scattered by lines and curves. The brightness of an object is determined by how much light it scatters per unit length. The edge of a polygon is a line and possesses nonzero length, hence it can scatter light, hence it can be visible. But the same goes for a Woman, who is a line and hence also possesses nonzero length. Only when the Woman is viewed end-on would she become invisible—and Abbott has already told us as much.

There is another possibility, though. Thin objects generally allow more light to pass through them than thick ones do. Flatland’s Women might, perhaps, be transparent. It seems clear that this is not what Abbott has in mind, but even if he did, a very thin parallelogram would also be virtually transparent. So would a very narrow isosceles triangle, especially near the sharp end.

It therefore seems necessary to assume that Women are opaque. A. Square would then have no more difficulty in seeing a Woman than he would in seeing anything else, and her (near) lack of a second dimension would be irrelevant. No wonder A. Square is not convinced by the Stranger’s argument.

Although A. Square can readily see Women, the Stranger will have problems. His visual senses are those of a three-dimensional world, and to him, brightness is determined by the amount of light reflected per unit area. A Woman, with (near) zero area, would not be visible to the Stranger, but a Polygon, with nonzero area, would be—except when viewed edge-on.

5 Abbott is using infinitesimal in the sense of “very small,” not in the technical sense of “infinitely small” (which requires some extensive contortions in mathematical logic before it can be endowed with a sensible meaning that is different from plain zero [see Ian Stewart, From Here to Infinity]). But again, there is a problem with the Stranger’s argument. If the height of an object is extremely small, then the extra amount of light that it scatters by virtue of its height is also extremely small. Therefore, height does not solve the visibility problem (for the Stranger, that is; there is no problem for A. Square in any case).

If the Stranger’s argument were correct, then by Abbott’s central analogy, a similar argument would apply in three dimensions. That is, in order for an object to be visible, it would have to possess some kind of “thickness” along a fourth dimension. However, the physics of light in ordinary space—which Abbott would have known about, being keen on the teaching of science as well as classics—requires no such assumption. The Stranger’s argument is paralleled in the preface to the second edition of Flatland, with its reference to “Extra-Height,” but Abbott uses this idea to demolish the argument that Flatlanders would not be able to see other Flatlanders unless they all extended slightly into a third dimension.

It rather looks as though Abbott’s critics (of the first edition) agreed with the Stranger and threw the argument back at him; Abbott responded correctly in the preface but failed to change the section, including the Stranger’s fallacious argument.

6 The Stranger objects to this suggestion: He is referring to a spatial dimension. The modern view is that brightness, being an independent quantity, could be considered an extra dimension—but not in the Stranger’s sense.

7 Having just said that the physics of light requires no additional small “hidden” dimension, I must point out that this is the case only in Newtonian physics and in today’s quantum physics. Tomorrow’s physics may change that statement. Or yesterday’s: In 1919 Theodor Kaluza (1885–1954) sent Einstein a proposal to unify gravity and electromagnetism by introducing a fifth dimension into space-time. Why don’t we notice the extra dimension? Because it is curled up very, very tightly and it is very, very small. This is precisely Hinton’s explanation of why the fourth dimension isn’t obvious, for in “What Is the Fourth Dimension?” he says,

The other alternative [to our being merely three-dimensional, if a fourth dimension exists] is that we have a four-dimensional existence. In this case our proportions in it must be infinitely minute, or we should be conscious of them. If such be the case, it would probably be in the ultimate particles of matter, that we should discover the fourth dimension.

The final remark was oddly prophetic, as we shall see in a moment.

Kaluza’s theory was improved by Oskar Klein (1894–1977) in 1926, but physicists lost interest in the Kaluza-Klein theory because it was extremely difficult to test experimentally. The idea of introducing extra dimensions into physics lived on, however. In recent attempts to devise a Theory of Everything (a unification of relativity and quantum theory), physicists have been led to postulate the existence of superstrings—particles that are not points but tiny multidimensional surfaces. Currently, the most popular version of this theory requires space-time to have its four usual dimensions plus six more, the extra six again being curled up into such a tiny region that they are imperceptible to any measuring instruments. The size of this curled-up region is expected to be roughly 1 Planck length—about 10–35 cm, the smallest distance that can be observed in a quantum universe. This idea is curiously reminiscent of Hinton’s remark about “ultimate particles of matter.” At any rate, physicists now think that our space-time might actually be ten-dimensional. See chapter 16 of Flatterland, “No-branes and p-branes.”

8 Abbott’s image here is mathematically and scientifically unnecessary, but he needed something tangible to carry his readers with him. Describing Flatland as the surface of a fluid has two narrative advantages. It makes it plausible that the inhabitants of Flatland can move at will across its planar surface: They are like thin wooden shapes floating on a pond. And it allows the Stranger to move through Flatland, like a fish rising from the deeps and breaking the surface of that pond. If Flatland were the surface of a solid, or just a rigid plane in its own right, this freedom of movement would be harder to explain. It is also possible that Abbott had in mind the “luminifer-ous ether,” a hypothetical fluid filling the whole of space, which Victorian scientists believed was the medium in which waves of electromagnetic radiation moved.

With suitable laws of physics, though, there is no need for familiar images of this kind. The plane of Flatland could be just a part of some larger space, and the physical laws could confine Flatlanders to this plane, while permitting other things (such as the Stranger) to exist in the larger space. In fact, current physical speculations place human beings in an analogous position. In “standard” superstring theory, our universe has ten dimensions, six of them being curled up so tightly that they cannot be perceived; human beings extend into those six extra dimensions, but they don’t notice them. However, there is a recent variant in which the extra dimensions required for superstrings can be imperceptible without being curled up into a tiny ball. Instead, our universe (and we with it) might be confined to a four-dimensional “surface” in a ten-dimensional space-time, just as Flatland is confined to a two-dimensional surface of a three-dimensional space. The other six dimensions can then be very big; we just can’t perceive them because our senses don’t point in those directions.

9 The Stranger (now revealed as a Sphere) can exhibit his shape to A. Square only through his intersection with the plane of Flatland because this is all that A. Square can perceive. The intersection is a circle, whose radius depends on the position of the center of the Sphere relative to that plane. As this position changes, so does the circle’s size. It is at its greatest when the Sphere’s center lies on the plane, and the intersection is then the “equator” of the Sphere and has the same diameter as the Sphere itself. It is at its smallest when the Sphere is tangent to the plane, at which stage it forms a single point—a circle of zero diameter.

10 A Spaceland observer sees a rigid body, the Sphere, rising. A. Square’s more limited perceptions enable him to see only a circle, which changes: Its size varies with time. It is important to understand that Abbott is not trying to develop the relativistic concept of time as a fourth dimension (or, in his analogy, of time as a third dimension augmenting Flatland’s two spatial ones). Imagine that A. Square could make a movie of the changing circle—a series of still frames showing the sequence of circular intersections created by the Sphere. Then the geometry of the Sphere is encoded, in a manner that is entirely adequate for mathematical purposes, in the sequence of still frames. It is not necessary to run the movie and turn those frames into motion over time. By moving through the plane of Flatland, the Sphere converts its third spatial dimension into something that a Flatlander can identify with the passage of time. But time itself is very different from the Sphere’s third spatial dimension, which exists at every instant of time.

11 This passage bears a distinct resemblance to act 1, scene 5 of Hamlet, where the ghost of Hamlet’s father can be heard speaking from beneath the stage, immediately prior to the line quoted by Abbott at the top of the cover of Flatland.

12 We sympathize with A. Square, for we also have difficulty comprehending four spatial dimensions. Our brains have evolved in a (spatially) three-dimensional world, and the nerve cells in the parts of the brain that detect and analyze visual perception have evolved an architecture that allows them to structure the incoming signals so that they provide an adequate internal representation of that external world. Here I am not merely saying that the brain is a three-dimensional object, although in a literal sense it is. The brain is a network composed of a large but finite number of nerve cells linked together by linear connections, so for most purposes the brain can be considered to be intricate but one dimensional (as is any mathematical network). What matters in a network is not its dimension but its connectivity—how many connections there are and what connects to what. A network that is connected like a grid in three-dimensional space is in effect three-dimensional, even if it is realized in the plane, and the same goes for four, five, or more dimensions.

In principle, then, a brain in three-dimensional space could evolve a neural network whose architecture mimics that of four-dimensional space, just as a brain in two-dimensional space could evolve a neural network whose architecture mimics that of three-dimensional space. However, such a structure would not evolve under natural conditions because there would be no systematic four-dimensional stimuli to cause it to do so. That having been said, such features as color and brightness in effect provide extra “dimensions” of stimuli, and our own visual systems are wired up to mimic these additional dimensions (so in a meaningful sense, we have six-dimensional circuitry inside our three-dimensional brains). But the brain interprets these extra dimensions as the “qualia” of color and brightness— the vivid sensory impressions with which the brain decorates them—and not as three more spatial dimensions.

13 We first learn that A. Square has mathematical leanings on p. 113, where we are told that he “. . . amused myself . . . with my favourite recreation of Geometry.” Abbott does not tell us A. Square’s profession, and the Sphere’s comment does not imply that he is a professional mathematician, only that the Sphere has noticed that he is mathematically inclined.

The following two and a half pages of Abbott’s text provide a systematic discussion of the combinatorics of n-dimensional “cubes” for n = 1, 2, 3, which can be summarized in the table at the top of page 148. Here vertex means the same as corner (or extremity in Abbott’s terminology), and I have used face to mean the (n - 1)-dimensional components of an n-dimensional object: endpoints of a line, edges of a square, faces of a cube.

Dimension	Name	Number of Vertices	Number of Faces
0	point	1	0
1	line	2	2
2	square	4	4
3	cube	8	6

Note that Abbott recognizes a point as a 0-dimensional object. He has no hang-ups about the number 0. For instance, the Flatland calendar has a year 0, making it arguably more sensible than our own.

A. Square (who knows only the first three lines of the table from direct experience) is set two puzzles of the type “guess what number comes next.” The first puzzle is

1, 2, 4, ?

and A. Square, being a mathematician, recognizes this as a geometric sequence (which in Abbott’s day was called a geometrical progression). In a geometric sequence, every term bears a constant ratio to the previous one; in this case, each term is twice the previous one. Thus A. Square instantly knows that the next term must be 8.

The second puzzle is

0, 2, 4, ?

and A. Square recognizes this as an arithmetic sequence (which in Abbott’s day was called an arithmetical progression). In an arithmetic sequence, every term has a constant difference from the previous one; in this case, each term is two more than the previous one. Thus A. Square instantly knows that the next term must be 6.

Abbott’s argument here is flimsy but interesting. The dimensions accessible to A. Square show simple numerical patterns. Moreover, the Spaceland reader (and the Sphere) know that these patterns continue to three dimensions. The patterns are all the more compelling in that they embody the two standard patterns taught in schools, both then and now. There are plenty of other types of sequences: The Encyclopaedia of Integer Sequences by Neil Sloane and Simon Plouffe lists 5,488 sequences of whole numbers, each obeying some specified rule of formation. One of the things that this book makes very clear is that “obvious” patterns need not continue. For example, what is the next term in the sequence 1, 2, 3, 4, 5? It could be 6—if the rule is “the whole numbers.” However, if the rule is “sums of two squares or three times a square,” the next number is 8. And if the sequence is the “quadruple factorials” (defined recursively by n!!!! = n(n – 4)!!!!), the next number is 12. Abbott’s sequence 0, 2, 4 would continue with 8 if it were the sequence of integer parts [n2/2] of squares 1, 4, 9, 16, . . . divided by 2. And 1, 2, 4 would continue 8, 16, 31 (not 32) if the rule of formation were “join n points on a circle in all possible ways, and then count how many pieces the circle is sliced into” (Figure 29).

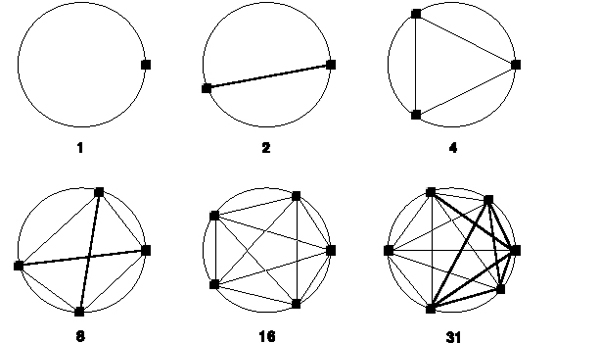
Figure 29 Into how many pieces do lines joining n points on a circle cut the circle? The early pattern does not continue in the “obvious” way.