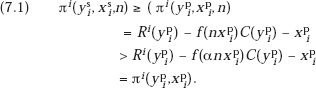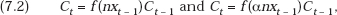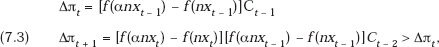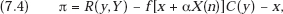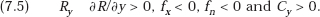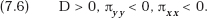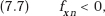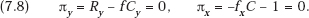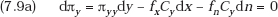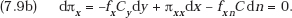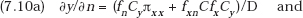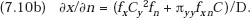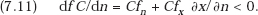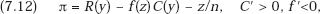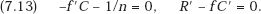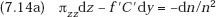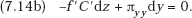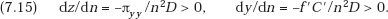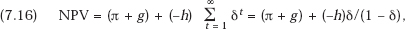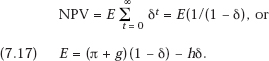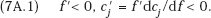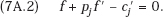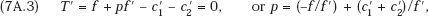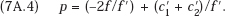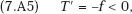CHAPTER 7
Oligopolistic Rivalry and Markets for Technology Trading
the knowledge of the man of science, indispensable as it is to the development of industry, circulates with ease and rapidity from one nation to all the rest. And men of science have themselves an interest in its diffusion; for upon that diffusion they rest their hopes of fortune, and, what is more prized by them, of reputation too. For this reason, a nation, in which science is but little cultivated, may nevertheless carry its industry to a very great length, by taking advantage of the information derivable from abroad.
—Say, 1819, 1834, p. 82
managers approached apparently competing firms in other countries directly and were provided with surprisingly free access to their technology.
—Allen et al., 1983, p. 202
BASIC THEORY
I turn now to a second mechanism that encourages and facilitates voluntary dissemination of new technology. The previous chapter discussed the profit incentive offered by the market mechanism for the licensing of proprietary technology. It also described the resulting consequences for efficiency in the use of innovations and for the rate of economic growth, arguing that the effect is generally beneficial. In the current chapter I will discuss the trading by competitors of the right to use one another’s technology, rather than the unilateral sale of such a right via licenses. It may appear at first glance that there should be little difference between the two cases, the only distinction being the nature of the reward: money versus payment in kind. We will see, however, that the differences are considerably more substantial. This chapter will describe the “technology consortia” that are implicitly created by the process of technology sharing. I will examine the nature of the market incentives for their formation, their stability (in contrast with the noted instability of price cartels), and their welfare consequences.1
Specifically, I will show in this chapter that:
Firms that pool their innovations gain a competitive advantage over firms that depend only on their own R&D resources. The resulting competitive handicap to nonparticipants in a sharing consortium can grow cumulatively as time passes.
Each participant in a technology consortium has a strong incentive to comply with its agreements, giving its trading partners full access to all of its proprietary technology information that it has promised. This is because cheating, in the form of failure to provide some promised information, can result in ejection from the consortium, with all its competitive disadvantage.
Membership in a technology consortium provides an added incentive to the member firm to invest in innovative activity.
The result is generally a contribution to the welfare of the public.
This implies that if antitrust policy is to serve the general welfare, in contrast to its justifiable position against inter-firm agreements on prices, it must exercise restraint in interfering with coordinated behavior by competing firms entailing the exchange of technological information on innovations.
Forms Taken by Technology-Sharing Arrangements
The arrangements for the sharing of technology that are encountered in practice are very heterogeneous. The exchange can have an explicit and formal structure, as when a trade association runs a research facility whose findings are available to all members of the association and whose expenses are divided among them on some predetermined basis. The same is true when two or more firms organize a research joint venture. Private and independent research organizations often offer the information they produce to all comers at a price. In addition, firms can, and do, exchange information that each has produced internally, by itself, and that could, instead, have been treated as proprietary.
This exchange also has many forms. The information can deliberately be disseminated on the explicit initiative of company personnel, with the knowledge and consent, or at least the toleration, of top management. Instead, company A may simply be prepared to answer inquiries from company B and to come to B’s assistance when it runs into technical difficulties, always with the understanding that such assistance is a two-way process. Firms sometimes welcome highly revealing plant visits by engineers and technicians from other companies, even when those companies are direct competitors, foreign or domestic. Some enterprises even agree, on request, to train the technical personnel from another firm in the use of an unfamiliar process or technique, expecting the favor to be reciprocated in the future. There are also very formal arrangements for the exchange of technology, employing instruments such as carefully drawn contracts and cross-licensing of patents, as was illustrated by real and substantial examples in the previous chapter. Throughout the chapter, I will use the term “technology consortium” generically to describe all of the technology-exchange arrangements that have just been mentioned.
Recently, the economics literature has begun to recognize that there are a number of reasons firms may want to share some of their proprietary technical information (for an excellent overview, see Katz and Ordover, 1990). The reason that is perhaps most often given (it is also frequently cited by businesspersons) is the high cost of the innovation process, which is more easily shouldered by a group of firms than by a single enterprise. This, and several other explanations that will be noted later, seems valid enough. However, this chapter will stress an entirely different market mechanism that can provide an incentive for technology sharing far more pervasive and powerful than those previously noted.
Complements and Substitutes in Innovation
Since, in practice, many firms seem willing to participate in technology sharing, as the evidence offered in chapter 6 indicated, they presumably expect to profit by doing so. A distinguishing feature of our model describing the nature of that gain is based on the difference between innovations that are substitutes for one another and, hence, mutually competitive, and those that are complementary.2
When two firms are working toward innovations that are, at least to some degree, substitutes, as is implicitly assumed by many models of competition and the innovation process, then their managements may well have a strong incentive to resist leakage of their proprietary technical knowledge. But the market incentives are reversed when, as often seems true in practice in large-firm R&D, the innovations in question are heterogeneous and complementary. This scenario is very different from Schumpeter’s, or from those of patent races and waiting game models in which all the competitors are after what is essentially the same technical goal: a given new product or process, say the design of a less expensive high-definition television receiver.
Here, in contrast, I will focus on an evolving product, for which innovations are small heterogeneous improvements introduced by different manufacturers of that same product. These improvements are typically complementary. In laptop computer manufacturing, for example, one producer may introduce an improved screen, another an improved keyboard, and a third may invent a way to make the laptop lighter and more compact. Each of these three firms has the choice of keeping its invention to itself. But if two of them get together and agree to produce computers combining the features each of them has contributed, they will be able to market a product that is clearly superior to what each could have produced alone. They are then likely to be in a far better position to meet the competition of the third manufacturer. Thus, I will say that the improved screen and the superior keyboard are complementary rather than substitute inventions.
In reality, both types of relationships occur. Thus, there are well-known examples of hot patent races that, by their nature, entail inventions that are close substitutes. But the normal operation of the large firm in an industry with rapidly evolving technology seems more often characterized by heterogeneity and complementarity. As has already been asserted here, the large firm is rarely the source of revolutionary new products or processes, and most of its innovative investment appears to be devoted to incremental improvements.3 In fact, it will generally be a coincidence if the R&D activities of two suppliers of a common product hit upon similar improvements, that is, upon substitute innovations. The model that follows, then, deals with the presumably more common case of complementary innovative results.
It should also be emphasized that, although the discussion will occasionally provide results that hold in the special cases of perfect competition or perfect contestability, the model does not assume that the markets take either of these forms.
The Technology-Consortium Model
Consider an industry containing n + 1 firms that are identical in all respects except that firms 1, …, n agree to share technical information with one another, while firm n + 1 keeps the results of its R&D to itself. Assume, to simplify the exposition, that each firm routinely spends the same amount on R&D per period, and that the expected return to this expenditure is the same for every firm. Most important, assume that the inventions of the different members of the consortium are generally expected to be different from one another and complementary, so that none of them can be used only as a replacement for one of the others. Finally, it is assumed, also for simplicity in discussion, that innovation expenditure is devoted exclusively to cost-reducing process innovations. That is, the innovation process is taken to make final products cheaper but no better. The only purpose of this inessential premise is that it permits quantification of the immediate benefits, making them easier to represent and interpret.
The public-good character of the information derived from R&D does not mean that it costs nothing to transfer information from the firm, A, that has produced it, to another enterprise, B, in a technology-sharing consortium. There is, in fact, evidence that the process of imitation typically has costs that are not negligible when compared with those of the earlier innovator.4 Nevertheless, firm B can expect a considerable net benefit from the information it obtains from the other n − 1 members of the technology consortium. Even if it could, eventually, get the same information through reverse engineering, industrial espionage, or other means, the empirical evidence indicates that a friendly transfer is typically far cheaper and quicker than a hostile one. In a rapidly evolving field, speed is particularly important because slowly acquired technical information is apt to be obsolete information.5
Suppose that B’s internal R&D is expected to reduce the cost of the firm’s final product by r percent per year. At the same time, because of transfer costs, B can expect a cost reduction from the information it obtains from A, or from any one other single member of the consortium, of only s percent (where s ≤ r). Then, if total R&D spending by each firm is x per year, and C0(y) is the initial period’s total cost of production of its output, y, its expected cost in the next period will be C0(y)[1 − r − s(n − 1)] + x, that is, its expected future manufacturing costs of final products will be reduced, not only by its own efforts, but also by the R&D of each of the other n − 1 members of the consortium.6 In contrast, the holdout firm, n + 1, which refuses to join the consortium and which, by hypothesis, starts off with the same costs as B, will incur the total expected cost C0(y)(1 − r) + x in the next period (since by hypothesis xn + 1 = x), which is clearly greater than the consortium member’s cost. Moreover, we will see that this expected cost disadvantage increases cumulatively with the passage of time. Beyond that, if the game is a repeated one and if the market happens to be perfectly competitive or contestable, with entry absolutely free, so that B’s expected profit is zero, the holdout firm will be faced with ever-growing expected losses.
The logic of the argument, then, is clear. So long as the firms are similar in terms of expected value of information output, and technological changes are predominantly complementary, a technology consortium gives its members a considerable competitive advantage, ex ante. It apparently will pay a firm, X, to hold out from membership only if its large size or other special circumstances lead it to spend so much more on R&D than do its rivals that the cost reduction it expects to achieve for itself will enable it to stay ahead of the cost reductions its competitors can achieve in aggregate through the formation of a technology consortium that does not include firm X.7
Formal Characterization of the Cost of Nonmembership
Let us now examine, a little more systematically, the market’s penalties upon the nonmember firm.
PROPOSITION 7.1. A firm that does not join a technology consortium of members otherwise identical with itself is automatically penalized financially by the market mechanism. (a) Its expected profits are lower than those of a consortium member; and (b) the expected opportunity losses continue through time and grow cumulatively.
That is, if two firms are identical in all other respects—in their market demand, their costs, and the returns to their R&D investment—but one has access only to the innovations it introduces itself, whereas the other exchanges information with other firms on their proprietary innovations, then the latter will be more profitable than the former. Moreover, the relative profit disadvantage of the nonmember continues and grows larger the longer it is excluded from the consortium.
This proposition is virtually self-evident, and it will be formalized only to introduce my model. To prove Proposition 7.1, as well as several subsequent results, I use the following notation, for simplicity suppressing subscripts that identify particular firms wherever that information is self-evident:
xk = x = |
firm k’s R&D expenditure per period, assumed identical for all firms in the market;8 |
yk = |
output per period of firm k; |
i = 1, …, n = |
the indexes identifying individual consortium member firms; |
j = n + 1, …, N = |
the nonmember firms; |
πi(yi,xi,n) = |
the total profit function of consortium member i; |
πj(yj,xj) = |
the total profit function of nonmember j; |
Rk(yk) = |
firm k’s total revenue per period; |
Ck(yk) = |
firm k’s total non-R&D cost in period zero; |
fk(zk) = |
the cost reduction factor for firm k in the subsequent period, where ∂fk/∂zk < 0 and where zi = nxi for consortium member i, |
zj = |
αnxj for nonmember j (so zk is a measure of the new information available to firm k); |
α < 1 = |
benefits lost from an information transfer because it is “hostile” rather than “friendly”; and, finally, ‘s’ and ‘p’ are superscripts referring to profit-maximizing values of the variables in question for those firms that share their information (s) and those that hold it proprietary (p), respectively. |
Here I use α < 1 to represent the fact that, though the spillovers of innovative activity bring benefits to nonmembers of the technology consortium as well as to members, the costs and benefits to the former are generally smaller, because it is more difficult to obtain technological information without the cooperation of its proprietor, and because such hostile technology acquisition takes longer and therefore is closer to obsolescence when the information is finally obtained by the nonmember. We may note also that we can, if we wish, take the variables in the model to refer to expected values, so that all of the calculations become ex ante in character.
Proof of Proposition 7.1. Part (a). Since, generally, for a technology-sharing firm, I, ypi and xpi are not the profit-maximizing values of yi and xi, we now have immediately
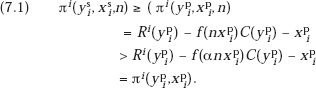
This is our desired result; the firm will lose out in terms of profits (or expected profits) if it declines to become a member of the technology consortium when all members spend the same amount on R&D.
Proof of Proposition 7.1. Part (b). The profit (opportunity) loss of the firm that finds itself excluded from the consortium is not just a once-and-for-all matter. Rather, it is an intertemporal stream of losses that grows cumulatively with time. This is easily proved by rewriting the two central expressions in (7.1) with the addition of time subscripts (and the omission of subscripts and superscripts that are obvious). We obtain for the consortium member and nonmember, respectively,
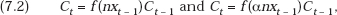
so that Δπt and Δπt + 1, the profit loss in periods t and t + 1 resulting from ejection from the consortium in period t − 1, become
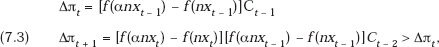
as we wanted to show.9
It should be emphasized that, although the motivation for membership in a technology consortium that has just been described is important and pervasive, the literature has offered other reasonable explanations for technology sharing. Reduction in the cost burden of R&D to each of the sharing enterprises has already been mentioned. This incentive is clear in the case of research joint ventures, but in arrangements such as royalty-free cross-licensing of patents its role is less obvious. The literature also mentions sharing incentives such as network externalities that only a group of enterprises can achieve, the benefits of standardization and compatibility that a consortium can arrange to have built into the new products of its members, and the possibility that the mutual benefits of an outward shift of the demand curve facing the industry as a whole may be achievable only by products that share all of the available improvements. For further discussion, the reader is once again referred to the admirable overview of the subject by Katz and Ordover (1990).
Welfare Consequences
I come, next, to some of the welfare consequences of technology consortia, where my mathematical model begins to pay off. In a sense, it is obvious that a technology consortium can generate welfare benefits by permitting wider and more rapid use of innovations, unless the sharing of information undercuts the incentive for R&D investment or leads horizontal competitors to engage in monopolistic types of behavior. It may seem plausible, for example, that colluding competitors will all agree to cut their expenditures on innovation to save the trouble and expense.10 But it will be proved next that if the innovations of the firms are complementary then information sharing will increase the profit-maximizing oligopolist’s spending on innovation.11 Moreover, the cost saving, in turn, will increase the profit-maximizing output per firm.
I emphasize that neither Proposition 7.2 nor Proposition 7.3, which follow along the same lines, implies that a technology consortium yields a socially optimal outlay on innovation by the firm. It still remains true that the externalities of innovation can be expected to lead to outlays that are generally less than optimal. I claim here only that the technology consortium tends to move matters in the right direction. It internalizes part of the externality by enabling an innovating firm, A, to obtain a substantial reward for its own innovation effort in the form of cheaper and quicker access to the innovations of other enterprises that are beneficiaries of A’s technology. Specifically, we have,
PROPOSITION 7.2. With a fixed number of profit-maximizing firms producing a single product and investing in cost-reducing R&D, if each firm in the consortium behaves like a Cournot oligopolist and there is complementarity among the research outputs of the technology-sharing firms, then a rise in the number of consortium members will increase each member’s outlay on innovation, as well as its output of the final product, and shift its total cost function downward.
Here, I assume that the number of firms in the industry is expected by the Cournot firm to be fixed, so that an increase in n + 1, the number of consortium members, entails an equal reduction in the number of nonmembers. On the Cournot assumption, this means that each firm will expect the total output of the remainder of the industry to be unaffected by a change in n. For convenience, n will, unrealistically, be treated as a continuous variable.
Proof of Proposition 7.2. Let the profit function of a consortium member (firm 1) be given by
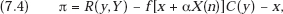
where R, C, y, x, and f have the same economic connotation as before, and
Y = |
the total output of all firms in the industry other than 1, which Cournot firm 1 assumes to be constant, |
X(n) = |
the sum of the expenditures on innovation of the n other members of the consortium, |
α = |
a constant, (0 < α < 1), this time representing the cost of “friendly” technology transfer, and |
D = |
the Jacobian determinant of the derivatives of π. |
Then we expect, by assumption,
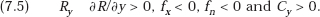
By the second-order conditions
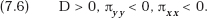
Finally, define complementarity between x and X(n) (where dX/dn > 0) as
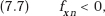
that is, a rise in X(n) increases the marginal cost saving yielded by a rise in x, firm 1’s expenditure on innovation.
Then the first-order maximization conditions for (7.4) are
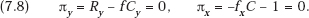
Setting the total differential of each of these equal to zero to determine what changes in y and x are needed to restore equilibrium after an exogenous change in n, we obtain
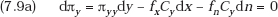
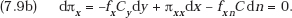
Thus,
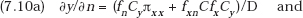
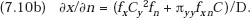
By (7.5), (7.6), and (7.7) it follows directly that (7.10a) and (7.10b) are both positive.
Moreover, the effect of a rise in n on firm 1’s total production cost for a given volume of output, y, is
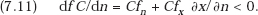
This completes the proof of Proposition 7.2. It is also clear that the same results all hold if the inventions are very weak substitutes, so that fxn is positive but relatively small. We can also prove, analogously:
PROPOSITION 7.3. Under the assumptions of Proposition 7.2, but if each consortium member expects every other member will make exactly the same decisions that it does,12 any increase in n, the number of firms that share the results of one another’s R&D, will shift the production cost curve of each firm downward. Each information-sharing firm will increase its output when n rises,13 and, if the marginal-cost-reducing returns to x, the firm’s investment in R&D, are increased by an increase in the technical information it receives from other consortium members (complementarity in their innovations), a rise in n will increase the firm’s R&D outlays.
Proof of Proposition 7.3. For simplicity, rewrite the profit function of a member of the technology consortium as
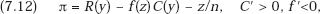
where z = nx is the total outlay on R&D by all the members of the consortium together. Differentiating in turn with respect to z and y, we have the first-order maximum conditions
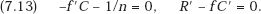
Equating to zero the total differential of the LHS of each equation yields
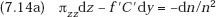
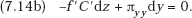
We obtain our comparative-statics results directly, using inequalities corresponding to (7.5), (7.6), and (7.7):
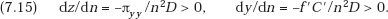
Recalling that C is the initial total cost function for the firm and that f is the function indicating the proportion by which that cost is reduced by invention, we also have ∂fC/∂n = (∂fC/∂z)(∂z/∂n) = f′C∂z/∂n < 0, so that the firm’s production cost, fC, is, ceteris paribus, a decreasing function of n. We can complete our proof by substituting x = z/n in (7.12) and obtain, by then repeating all the preceding steps, the result that ∂x/∂n > 0 iff f″ is negative, zero, or positive and sufficiently small. This can be interpreted as the premise that the innovations are complementary, independent, or very mild substitutes. That is, in all such cases, technological information exchange will actually stimulate each firm’s outlays on innovation.
The result that, under the premises of either proposition, an expansion in the number of members of the consortium reduces production cost is not, by itself, conclusive evidence that efficiency is increased. For, with a given y, it is still conceivable that spending on R&D will increase by more than the cut in production cost. When n increases, so long as the resulting rise in x (the firm’s innovation outlay) does not exceed the reduction in its cost contributed by access to the technology of the new consortium member(s), this, obviously, will not happen. However, if a larger value of x were selected, this would presumably indicate that the yield of the incremental R&D outlay more than covers this enhanced expenditure. Certainly that must be true if the markets are perfectly competitive or contestable, and there is at least a presumption that the same conclusion holds in a considerably broader range of market conditions. This, then, is the sense in which a rise in the number of members of the consortium can be presumed to be welfare increasing.
It is important to observe that the same conclusions, as well as the results of Propositions 7.2 or 7.3, must necessarily also apply to the formation of a technology consortium. This follows because the decision of n firms to create a technology-sharing consortium can be interpreted simply as an increase in the number of its members from zero to n, and the result then follows directly. The creation of a new technology-sharing consortium can increase spending on innovation, increase output, and reduce cost.
None of this is, however, meant to imply that it is impossible for a technology consortium to harm the general welfare. On the contrary, it raises at least two (closely related) dangers. If such a group learns to coordinate its decisions closely, one cannot rule out the possibility of perversion of the technology consortium into a conspiracy either to fix prices or to suppress innovation outlays, or both.
There is one apparently characteristic feature of such consortia in practice that seems to reduce these dangers substantially. In every technology-exchange program of which I am aware, the negotiation and supervision of the arrangements are strictly bilateral. That is, even though firms A, B, C, and D are members of the same consortium, in the sense that they all trade information with each of the others (and each is well aware that the others are doing so), A, for example, will have a separate agreement with each of the others. Its exchange contract with B may be very different from that with C or D. The four firms will never meet together nor will the group as a whole share communications. Such a pair-wise mode of operation seems unlikely to permit the degree of coordination that is necessary for effectiveness in fixing prices or in agreeing to hold down R&D outlays.
It should also be noted that the welfare issues raised by my discussion of technology-sharing consortia go well beyond the subject of innovations and their use. In particular, my analysis raises the obvious questions about the dangers to the public interest of inter-firm agreements. It is generally accepted, for example, that price-setting coordination by horizontal competitors is damaging to the public interest, and that it will normally end with final-product prices higher than they would have been if those prices had been arrived at independently. It is on these grounds that the U.S. courts hold such price fixing to be a per se violation of the law, that is, one for which there can be no justification, no matter what the circumstances.
But this does not mean that all coordinated acts by independent enterprises are damaging to the public interest. Indeed, the preceding discussion has demonstrated that this is not always so. This general issue, with its important implications for antitrust activity, particularly in relation to innovative activity and growth, is examined more fully and in more general terms in the appendix to this chapter.
THE STABILITY OF TECHNOLOGY-SHARING CONSORTIA
Incentives and Disincentives for Cheating
The economic literature is replete with discussions of the inherent instability of price cartels—the difficulty of getting agreement on the output quotas for the individual members, the incentives for cheating, the monitoring difficulties that encourage cheating, and the resulting vulnerability of the entire enterprise. To get at the stability issue for technology consortia it is instructive to contrast these consortia with price-setting cartels.
Despite the loss of profit resulting from exclusion from a technology consortium (Proposition 7.1), it does not follow that incentives for cheating are absent. Such incentives do exist, for both price and technology agreements, at least in the short run. In a horizontal pricing cartel, a member can clearly profit by surreptitious price cutting to achieve sales above its quota, even though it shaves the monopoly profits offered by the cartel price and harms other members. In a technology consortium, the obvious cheating scenario involves a member that hopes to be able to profit from the information that the other members provide, but at the same time tries to retain a competitive advantage by keeping (some or all of) its proprietary technology to itself. Thus, in both cases dishonesty can be the most (immediately) lucrative policy.
In the long run, however, the stability properties of price cartels and technology-exchange consortia are very different. Here I must first note that the prospects for success in cheating are far from identical. In a horizontal price cartel it pays the customer to act as co-conspirator with the cartel member that wishes to cheat. The reduced price will be reason enough for the customer to avoid revealing the defector’s secret. So cheating is not always easy to detect.
In a technology consortium, in contrast, there is no customer whose acquiescence is required for successful cheating. Technology exchange is normally a game that is played many times, and this is a powerful force for stability. Firms have many ways to monitor one another’s technology, and a variety of clues can indicate cheating: low prices suggesting an undisclosed process innovation that permits long-lasting cost reductions, or changes in product characteristics, or industry gossip, or other signals. These can all arouse the suspicion that the firm in question is not giving out all the information it claims to be ready to provide. In such cases, other members of the technology consortium can readily reciprocate by becoming more selective in passing information about their own technological advances to the suspect enterprise, or by ceasing to do so altogether. As in so many situations, reputation becomes an invaluable asset in a much-repeated game of technology exchange (see below).
So far, I have merely pointed out that information-exchange cheating is apt to be discovered eventually, and that the firm that does cheat is likely to be deprived of the benefits promised by consortium membership when that happens. But that is also true of a price cartel. However, there are at least two special features of a technology consortium that can be more effective in discouraging cheating and another that protects the consortium from collapse, even when some cheating occurs.
The first of these special features is the option available to the consortium members of abandoning an informal information-exchange arrangement that relies largely on mutual trust, and substituting a more formal program in which the trades are specified explicitly. Perhaps the most straightforward form this can take is cross-licensing of patents, so that each party knows exactly what it is getting from the other. Such an agreement clearly restricts the opportunity for cheating, and may help to explain the apparent recent rise in patenting.
There are other formal arrangements that can be used to discourage cheating. For example, a real-world arrangement, which I have not found in the economic literature, is used by at least several real firms of which I am aware in negotiating their technology-exchange program. Any two such firms (call them A and B) meet at intervals to negotiate the monetary compensation to be paid by A to B (or vice versa) for any shortfall in the value of the innovations that A expects to provide to B in the period before the next negotiation, in exchange for B’s innovations that will be given to A. Such an arrangement gives each firm a strong incentive to reveal all or most of the inventions currently being worked on in its R&D facilities and almost ready for direct use or commercial introduction. Any such invention whose existence is concealed by A simply increases the amount it must pay to B on the balance equalization account, and increases A’s payment obligation to B by an amount approximating the expected value of the undisclosed innovation. There is, of course, an adverse selection problem here, because the innovating firm is apt to know more about the value of the invention than the purchaser of its technology does. Yet, if such negotiations are repeated at regular intervals, each firm will learn the trustworthiness of the other party’s evaluations of its own inventions. The value of a reputation for integrity in such a bargaining process can, then, reduce the adverse selection problem.
The second attribute of a technology consortium that discourages cheating is more automatic than the various options for formalization of the exchange arrangement, two of which have just been described. Proposition 7.1’s proof that nonmembership in the consortium constitutes an ever-growing opportunity loss implies that ejection from the consortium in a repeated game is likely to be very costly, particularly in the longer run.14 That is, the penalty of ejection for discovered cheating can be far harsher than in a price cartel. Indeed, in those special cases where markets are highly competitive or highly contestable, so that maximum long-run profits are close to zero, the ejected technology consortium member will be condemned to growing losses and to eventual insolvency. In such circumstances, firms with a considerable investment at stake and with an ambition for the long-term future will find it essential to cultivate a reputation for integrity, just as is pointed out in the literature on product quality in markets with imperfect consumer information. Thus, technology consortia have a strong and growing incentive against cheating.
This leads immediately to another distinctive and pertinent feature of technology consortia: their striking invulnerability to defection, in sharp contrast to a horizontal price cartel. In the latter, as is well known, once the members begin to suspect cheating on the part of the others, it becomes dangerous for them to continue to obey the cartel’s decisions. The horizontal cartel member that continues to insist on the high product prices specified in the cartel agreement is likely to find itself without customers, all attracted away by defecting price cutters. That, ultimately, is why horizontal price cartels are considered to be so unstable.
In a technology consortium, in contrast, we see that even when some members defect, each remaining member will continue to enjoy the benefits of access to the R&D of the other remaining members. That is the obverse implication of Proposition 7.1—that the members of even a small consortium will derive an advantage over nonmembers. If one member is suspected of cheating, the rational reaction is to eject that firm from the consortium and to continue exchanging information with the remaining members. And, certainly, a defection by one member does not eliminate the danger to another member when it does anything that risks ejection from the consortium. Consequently, a technology consortium can easily survive a case of (discovered) cheating. So it is far less vulnerable to the prospect that one or a few members will succumb to this temptation.
Still, technology consortia are not absolutely immune from destabilizing cheating. A prime source of temptation is the fact that even routine R&D can sometimes turn out ex post to yield a breakthrough of enormous and unusual value, even where the firm had no reason to expect it ex ante. When such an extraordinary advance occurs the innovator firm may be strongly tempted not to share it with others, particularly with its horizontal competitors. Two things weaken this temptation to some degree. First, the fact that the imitation process usually entails some lag means that the original innovator often can enjoy a period with no competition in the invention and can therefore obtain considerable benefit from it, even if it provides information about it to the other consortium members promptly and fully. In addition, as we have seen, the costs of permanent exclusion from the consortium as the penalty for cheating can be very great. Consequently, only if the value of the development is very substantial will it be rational to succumb to the temptation to defect because it transpires ex post that the R&D investment has been unexpectedly successful.
Toward Formalization of the Stability Issue
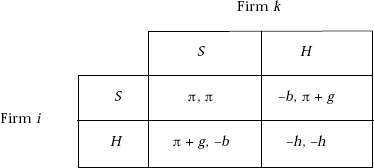
The stability of a technology-sharing consortium can be investigated somewhat more formally in terms of repeated games.15 I start off with a structure that resembles a prisoners’ dilemma game. If the members share information they all get higher payoffs than if they all fail to do so. However, firm j will obtain a reward that is even higher if the other firm, k, really shares whereas j succeeds in hiding its invention and in concealing the fact that it is doing so. This situation is illustrated in the payoff matrix of the stage game, Payoff Matrix 1, in which the notation, as well as the discussion that follows, is based on the work of Abreu, Milgrom, and Pearce (1991).
Here, the two available strategies for each player are Share (h) and Hide (H); π is the return to each sharer if both players share, and excess profit, g, is earned by the firm that is able to exploit the other enterprise’s sharing of its technology but succeeds in hiding its own. Let us take π, g, and b all to be strictly positive, with −b < −h. Then the symmetric pure strategy profile (S,S) clearly yields payoffs that dominate or Pareto-dominate the other symmetric pure strategy profile (H,H). However, the mutual concealment strategy profile (H,H) is the unique dominant strategy equilibrium, that is, either firm will do better by choosing H, given any fixed decision by the other enterprise.
But if this is a repeated game that is played at t = 1, 2, …, and the payoffs in Matrix 1 are per period payoff values, then the payoff (π,π) can be sustained in the long run. One equilibrium strategy pair in the repeated game that can in suitable circumstances yield the collusive payoff (π,π) is the “trigger strategy” profile.16 This strategy is a decision by each firm to play “Share” so long as the other does so, but to play “Hide” forever after, once the other enterprise fails to share. If one firm, say j, expects to conceal in some period, call it the initial period, and it believes that the other firm has adopted the trigger strategy that will come into play after period 1, when j’s concealment is discovered, then it will no longer earn π + g, or even π, per period forever. Instead, taking δ as the pertinent discrete period discount factor, j can expect a stream of earnings whose net present value (NPV) is
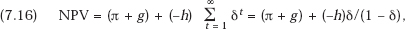
PAYOFF MATRIX 1
so that, taking this to be equivalent to the constant per period flow of earnings, E for t = 0, 1, 2, …, we obtain
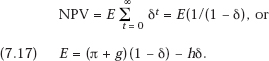
Adoption of the trigger strategy will induce two profit-maximizing firms to act in a manner that yields the sharing equilibrium and renders that equilibrium stable iff E ≤ π, that is, if and only if the earnings expectable from this course of action exceed those that can be expected from concealment of proprietary technical information.
From the point of view of the potential defector, the story, so far, can be summarized in Payoff Matrix 2, where g represents a “one-shot” gain. However, as it stands, with no explicit role assigned to the other members of the consortium, the logic of the construct is the same as that of the prisoners’ dilemma game. It is only the presence of the other consortium members that changes the argument and carries it beyond the prisoners’ dilemma/repeated game story, which asserts merely that the one-shot gains from cheating do not exceed the future loss from punishment.
|
Inclusion
in
Consortium |
Exclusion
from
Consortium |
Share |
0 |
— |
Hide |
g |
−b |
PAYOFF MATRIX 2
One drawback of the preceding construction is that it is not “renegotiation proof” (on this, see, e.g., Bernheim and Ray, 1989; Farrel and Maskin, 1989; and Pearce, 1987/1990). After a defection in the two-player case, both firms receive low non-cooperative payoffs in the punishment phase that follows. Might they not then be tempted to promote their mutual interests by renegotiating to achieve a more cooperative mode of operation? However, if that is anticipated, the entire incentive structure of the supposed equilibrium unravels. More sophisticated structures are needed to evade this problem (see the papers just cited).
In our setting, the issue has a nice resolution that rests on the multiplicity of other firms in the consortium. A defecting firm is punished upon detection (though this may occur only with a lag) simply by exclusion from the consortium. The special feature that characterizes this case is that the non-defecting firms have no need to break up their profitable sharing arrangement. They can go on indefinitely, sharing their information, while the defector continues to suffer the consequences of exclusion. In contestable markets, this argument can be strengthened further, because the place of the defecting firm can be taken over by a new entrant.
In short, this formal analysis lends some systematic support to an assertion in the previous section about sources of stability of a technology-sharing consortium. This is the argument that the likelihood of continued profitability of membership in a technology consortium, even after defection of one or even several of its members, contributes stability to this form of association of a sort that is absent in a horizontal price cartel.
Of course, this discussion is a simplified treatment of its subject. A richer model is a dynamic Markov game in which the state variable (the accumulation of each firm’s technical information) increases during periods when sharing goes on. The other main oversimplification is that concealment of information is treated here as though it were perfectly or nearly perfectly observable, though it is in fact likely to be recognized by other firms only imperfectly and only after some delay. Exploration of these effects leads us to the analysis in Abreu, Milgrom, and Pearce (1991), to which the reader is referred for further details.
CONCLUDING COMMENTS
This chapter, along with chapter 6, has shown that firms have much to gain by licensing their technology at a suitable fee or by joining a technology consortium, and that they can suffer severe competitive penalties if they refuse to do the latter. However, one must not jump to the conclusion that the market mechanism offers no impediments to the dissemination of technology. In practice, a substantial number of firms seem to hold out and try to keep the results of their R&D proprietary. The number of patent infringements lawsuits (e.g., Polaroid v. Kodak, Lotus v. Borland, and Litton v. Honeywell) is clear evidence that firms do sometimes take this position. This can be rational for a number of reasons, most notably because of market imperfections.
For example, resistance to technology sharing can benefit firms financially if product innovations result in product heterogeneity that permits the coexistence of several islands of (perhaps moderate) monopoly power. If the innovation process yields distinctive products to each firm in the industry and each of the products commands some degree of customer loyalty, then every firm may be able to charge a price above its competitive level. In contrast, where circumstances impede successful collusion and similar products are offered simultaneously by several rival enterprises, supercompetitive profits are generally precluded. This may be one of the more compelling explanations for unwillingness to join a technology consortium—the desire to ensure that one’s own product remains quite different from those of other firms. Sometimes that may be the only way of obtaining and keeping a degree of market power sufficient to yield substantial and continuing economic profits.
More generally, we may recognize that unwillingness to provide a technology license to a competitor in a final-product market constitutes a form of vertical foreclosure. In effect, it is a case in which the (upstream) proprietor of a valuable input (the innovation) is motivated to prevent its use by a downstream competitor firm—a rival supplier of the final product in which that input is used. The reader is referred to the substantial literature on vertical foreclosure for extensive discussion of the circumstances in which this type of behavior is to be expected. Here, it is important, however, to take note of the general conclusion that concerted pricing and other related types of behavior by horizontal competitors are much the more serious anticompetitive threat, and that the market generally offers business substantial incentives for reasonably desirable behavior in its vertical relationships.
In this and the previous chapters, enough evidence has been reported to give credence to the view that the market does a far better job of technology dissemination than is, by implication, credited to it in the literature of economic theory. It has also been shown that, by internalizing the spillovers of knowledge production, technology consortia can even help to reduce the market’s incentives for underinvestment in innovation.
All in all, the analysis suggests once again that we need to reconsider the judgment that the market performs quite well in terms of static economic efficiency but that, because of inadequacy of expenditure on innovation and unwillingness to share technology, it is highly defective in the intertemporal sphere. Still, the discussion up to this point has said little about what is most frequently cited in the literature as an obstacle to efficiency in investment in innovation—the externalities (spillovers) that are generated by the activity. The next chapter will turn to that issue.
APPENDIX
WHEN IS COLLUSION SOCIALLY BENEFICIAL?
On the open range it was first come, first served, a principle that invited abuse … all involved understood that they faced the dilemma of the commons, where each individual’s pursuit of self-interest, in the form of grass for more of his cattle, threatened the ruin of all, in the form of degradation of the range … [Theodore] Roosevelt addressed this issue … [creating a stockmen’s organization] to deal with overgrazing, and other shared concerns.
—Brands, 1997, p. 186
We are used to the idea that collusion among firms is (often quite legitimately) presumed to be damaging to the public interest, and that the antitrust authorities are fully justified in taking coordination of prices to merit prohibition per se—as inexcusable in any circumstances. One reaches that conclusion when considering price as the matter being decided upon and when the coordinating parties are horizontal competitors. But, as has been shown in this chapter, and as those who have studied the issue know, joint decisions can in some general cases materially promote the public interest when those decisions deal with matters other than price. Even coordination of prices can be desirable if the firms involved are vertically, rather than horizontally, related. Indeed, this is widely recognized by antitrust authorities, who, for example, take a more favorable view of vertical coordination than of horizontal coordination and have frequently avoided interference in research joint ventures. The central point of this appendix stems from the key welfare observation in the body of this chapter that, with important exceptions, coordination on innovation and on the supply of proprietary technical information to competitors can be highly beneficial to the economy, enhancing both its static efficiency and its growth. The policy implication is that regulatory agencies and the courts should exercise extreme restraint in interfering with such joint decision-making, though they should maintain some degree of vigilance to ensure that it does not transform itself into anti-competitive behavior that profits those who undertake it at the consumer’s expense.
Preliminary: Vertical Price Coordination as an Illustration of Virtuous Collusion
It is generally recognized that the prices adopted by horizontal competitors will normally be higher than those arrived at independently. However, the opposite has long been known to hold where the firms are related vertically. To demonstrate that inter-firm coordination can sometimes be desirable, it may be useful to begin with an explicit recapitulation of the vertical price coordination argument. For this purpose, I provide a formal proof—with no pretense to novelty—confirming that the coordinated final-product prices of two firms that are vertically related profit maximizers will be lower, in total, than the sum of the independently adopted prices of the two final-product components they supply and that together constitute the final-product price paid by the consumer. The proof is simple and compares the price that maximizes the combined profits of the two firms with the Cournot equilibrium prices individually arrived at.17
Let
pj = |
the price charged by firm j for its component of the final product, |
p = p1 + p2 = |
the final-product price, |
f(p) = |
the final-product demand function, |
cj(p) = |
the cost function of firm j, and |
T, Tj = |
the corresponding profits. |
We can assume
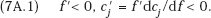
Then, differentiating firm j’s profit function partially with respect to its own price, we obtain the first-order Cournot maximum condition for j:
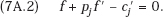
Similarly, the combined profit maximum requires
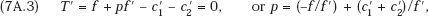
where both terms of the RHS of the last equation are positive, by (7A.1). Thus, (7A.3) gives us the final-product price that maximizes the combined revenues of the two firms. To find the corresponding price in the independent-decision Cournot equilibrium, add the equations (7A.2) for the two firms, j = 1, 2, and solve for p, yielding immediately
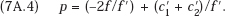
Substituting this price into the LHS of the first equation in (7A.3) we obtain after straightforward manipulation
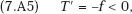
so that at the Cournot price the marginal combined profit is negative. In other words, if the profit function is concave, a reduction in the final-product price from the Cournot level is necessary for maximization of the combined profit of the vertically related firms. Q.E.D.
Here, then, we have a clear case in which coordinated action—shall I say collusion—is socially beneficial. This confirms that coordination of the decisions of several firms is demonstrably not necessarily damaging to the public interest. (For an intuitive explanation of the result, see footnote 17 above. The discussion will return to this explanation in the following section.)
We have already seen that beneficial welfare results can follow from coordination on decisions related to innovation. Evidently, coordinated decisions and activities by otherwise independent firms, even between horizontal competitors, can sometimes be damaging, sometimes beneficial, in terms of the public interest. Let us consider whether more can be said toward generalization of the discussion.
When Is Inter-Firm Coordination Beneficial? Toward a Common Thread
The discussion has provided several examples in which “collusion” among the suppliers of a product can enhance economic welfare, the general presumption to the contrary notwithstanding. The examples may seem to be totally unrelated. The case of pricing decisions by vertically related suppliers is different from that of the providers of innovation and of access to their private intellectual property—and both of these differ substantially from the example (in the brief opening quotation on page 114 about Theodore Roosevelt) involving prevention of overgrazing by the herds of cattle of competing beef suppliers.
Yet there is a common element that seems to help explain them all and that may well indicate why there exist such significant exceptions to the well-grounded presumption against coordination by rival enterprises. In theoretical terms, the answer is suggested by the literature that culminated in the Arrow–Debreu theorems, asserting that, in the absence of externalities, perfect competition will yield equilibria that satisfy the requirements of economic efficiency and Pareto optimality. Since inter-firm coordination can be interpreted as a move away from a competitive regime, this immediately suggests that it will be beneficial only where externalities are present. The well-understood overgrazing issue supports this observation. It is the case of the tragedy of the commons, in which overuse results when users do not give full weight to the external damage their usage imposes on the others who depend on the availability of the common property.
Once this is recognized, it is easy to see that the externalities issue is critical for both of my other illustrations of beneficial coordination. The price of the final product of two vertically related firms will exceed the profit-maximizing level and, incidentally, will presumably reduce consumer welfare because each of the two firms takes no account (or at least inadequate account) of the external damage that a rise in its own price does to the sales volume of the other. For example, when considering a rise in its prices, an independent producer of pharmaceuticals will ignore the loss to a maker of the capsules in which the former’s medications are enclosed, and the capsule manufacturer will behave in the same way. But, to maximize their joint profits, the price decided upon must take these detrimental external effects of too high a price into account, and so coordination will result in a lower price for the final product than would emerge from independent decision-making.
In the case of innovation, the role of the pertinent externalities is even more obvious. For innovation is a prime example of a product with enormous beneficial externalities. Coordination among the innovative firms helps to internalize the externalities, increases the incentive for investment in the innovation process, and reduces the avoidable costs that must be incurred by firms that might benefit from the innovations if their acquisition of these benefits is prevented or impeded by the proprietor of the innovative intellectual property, or even if the proprietor chooses not to help the other firms in the process of obtaining the requisite information needed to adopt innovations and to put them to effective use.
This suggests a general hypothesis about the circumstances in which the effects of inter-firm coordination will have beneficial consequences. Such benefits can be expected when the activities of each or most of the firms in question generate substantial externalities whose victims (or beneficiaries) are or include the other firms in the group. As is well recognized in the literature, where such externalities are present and substantial, uncoordinated behavior can result in substantial static inefficiency and, because of the crucial role of innovation in the growth process, it can also lead to substantial intertemporal inefficiency as well. Such a case is patently an opportunity for material enhancement of the general welfare via beneficial coordination, using any of a number of mechanisms ranging from Pigouvian taxes and subsidies through voluntary coordination, that is, “good collusion” among the affected firms.18
It may perhaps appear that, by tying the possibility of desirable coordination to the presence of externalities, I have reduced it to a very special case. But a moment’s consideration will confirm that it is inappropriate to treat this case as an exception. Rather, to paraphrase Marx, it may be more to the point to consider it as an instance where the rule becomes the exception and the exception (frequently) becomes the rule. Nowadays, we are well aware of the importance and pervasiveness of externalities in the economy. The dangers of overuse of public goods as common property are also well recognized. But, above all, the significance of the issue for innovation and growth, which, in turn, are so crucial for future economic welfare, means that it cannot be deemed to be a special issue of limited general importance.
Implications, Particularly for Antitrust Policy
There is much more that can be said about the subject. For example, a good deal can be reported about the magnitude of efficient technology-licensing fees and about the extent to which one can or cannot rely upon market forces to yield fees of that magnitude. But this is not the appropriate place to go into these details (for fuller discussion, see chapter 13). Enough has been said to enable us to offer some tentative conclusions.
First, it would appear from the discussion that the performance of the market in terms of the quality of resources devoted to innovative activities, and the market’s dissemination of the results of those activities, is considerably better than standard economic analysis may suggest. In particular, the degree of internalization of the externalities of innovation that technology trading and licensing permits may contribute substantially to economic efficiency. Second, it follows that innovation is an activity in which inter-firm coordination, even among horizontal competitors, can bring substantial welfare benefits. If further exploration supports this conclusion, it follows that the antitrust authorities’ willingness to show forbearance in their toleration of research joint ventures and technology licensing is fully justified.
Yet two amendments of the prevailing approach may well prove desirable. Where there has been no explicit announcement of policy by the authorities, indicating as specifically as possible what types of coordination and of what degree will meet with no interference by the agency, and in what circumstances they will so forbear, firms may well feel that a threat overhangs activity that they have reason to consider benign. I have heard businesspersons assert that this continuing threat has a chilling effect on legitimate inter-firm cooperation, despite the tolerance of the authorities in the past. If so, something may be gained from an attempt by the regulatory authorities to minimize this sort of uncertainty.
Finally, it may be equally desirable to have a public pronouncement indicating just what the authorities will seek to prevent. In particular, when there is reason to fear that industry expenditure on R&D is less than optimal, they should make it explicit that any attempt by the participants in a technology consortium to fix industry expenditure on innovation will be looked upon as unfavorably as price fixing.
___________
1. For an illuminating paper that studies learning by firms from one another using a theoretical orientation somewhat similar to that employed here, see Petit and Tolwinski (1993). See also the very important articles of D’Asprement and Jacquemin (1988) and Katz and Ordover (1990).
2. The special role of complementarity and substitution in innovation has also been emphasized by Nelson (1990); and see also Merges and Nelson (1994). It has also been studied, in another context, by Young (1992).
3. Thus, Levin reports, on the basis of his systematic study, that “technological advance in the electronics industries has been much more ‘cumulative’ than ‘discrete’” (1988, p. 427). Rosenberg’s work (e.g., 1976, p. 66, fn) has also emphasized this point, and has provided an abundance of illustrations.
4. “Our respondents from the industries producing aircraft and complete guided missile systems—canonical complex systems—reported that it would cost a competent imitator more than three-quarters what it cost the innovator to come up with something comparable, even if there were no patent protection at all” (Nelson, 1996, p. 64). The survey referred to here is described in Levin et al. (1987), which contains much valuable material on the costs of imitation.
5. For more on the general subject, see Mansfield, Schwartz, and Wagner (1981) and Teece (1977).
6. In addition, such an ex ante sharing arrangement clearly provides the firm insurance against the risk that its own R&D effort will turn out to yield little of value in any given year.
7. Even then, or when a firm’s R&D organization is superior in ability to that of its rivals, participation in a technology consortium can be profitable, as will be argued presently and as the example of IBM in the previous chapter clearly confirms.
8. Later, in Proposition 7.2, the choice of value of x is calculated explicitly on the premise that each firm follows a Cournot strategy. Except in the model used to derive Proposition 7.3, the premise that the value of x is the same for every firm plays no essential role.
9. The discussion has described the model in terms of ex ante sharing, in which each consortium member agrees to supply information on the output of its R&D activities over the selected future period. However, it should be noted that the mathematical discussion is not dependent on that assumption in any way. It is equally applicable, for example, to a consortium that operates through cross-licensing of the patents it holds on its past inventions. Thus, the results derived so far, and (except where otherwise noted) those that follow, apply to a broader spectrum of technology-sharing consortia, and not only to those with ex ante sharing.
10. For a fuller discussion of these problems, see Shapiro (2001).
11. The model assumes that the firm’s behavior is of the type described by Cournot (1838). However, it is not difficult to show that the result is more general.
Levin’s evidence seems to provide some empirical underpinning to this result, even though it has sometimes been suggested in the theoretical literature that (unintended) information sharing should discourage expenditure on innovation by the firm. Thus, note Levin’s comments on the prediction of Spence’s model “that spillovers discourage R&D investment but may be conducive to rapid technical progress.” Levin indicates that his results, “though only suggestive, give some support for the latter hypothesis, but none for the former” (1988, p. 427).
12. This term can be interpreted to mean either that the outcomes are symmetric or that the choices are made jointly. Here I mean the former—that, because the firms are all similarly situated, their profit-maximizing decisions on outputs and investment in R&D will be the same, and that experience will have led each firm to recognize the identity of its own behavior and that of the other members of the consortium.
13. For a similar result for the case of cooperation in R&D activity (in contradistinction to the sharing of the results of independent R&D activity), see the very nice paper by D’Asprement and Jacquemin (1988).
14. The contrast of the cost of nonmembership in a technology consortium, relative to a price cartel, is significant here. Nonmembers of a price cartel benefit from any price increase the cartel is able to impose, and the nonmember may even be better off than the member, because the former makes no commitment to reduce its output. The nonmember of a technology consortium benefits only via the innovation spillovers and, as we have seen (Proposition 7.1), it suffers a growing competitive handicap.
15. For help in the formulation of this section, I am deeply indebted to Professors Dilip Abreu and Zsuzsanna Fluck.
16. Throughout, I measure payoff in terms of a constant per period equivalent. That is, if a stream of payments has an expected net present value (NPV), and δ is the per period discount factor, then the constant per period flow equivalent of that stream is an amount, E, whose discounted present value summed for t = 0, 1, 2, …, is also equal to NPV.
17. The argument may seem similar to the “double marginalization” analysis based on Spengler’s justly noted article (1950). However, the derivation here deals with a more general situation, and does not depend on the firms constituting a succession of production stages, with a compounding of markups on successive stages. Rather, as Ruffin points out in an extremely valuable paper (forthcoming in 2002), the result stems from the work of Cournot ([1838] 1897, pp. 99–103). It entails two firms, each of which produces a component of the final product that may or may not represent different stages of production. In this scenario, each firm neglects the external damage to the other firm in the form of lost sales when the former raises the price of its component, so that the sum of the individual component prices exceeds the profit-maximizing price of the final product. Ruffin extends the result to a general multi-firm case.
18. This is a point I have argued for literally half a century, when I suggested in my first book that externalities are the primary underpinning for any economic role of government (Baumol, 1952).