
What Is Time?
Actually, nobody has the faintest clue what time really is.
Why is time always running forward and never backward? Or in circles? Would backward-running time be possible at all? Is it possible to send messages, or even to travel, back in time? The reason physicists discuss the possibility of time travel at all can be traced back to the theory of general relativity.
The concept of a universal and ever-increasing time that is consistent for all observers came to a sudden end when, in 1905, a technical expert third class in a Swiss patent office used his spare time—and sometimes also his work time—to think about the universe.1 Naturally he had to hide his notes and calculations hurriedly under his desk whenever his supervisor entered the room. Albert Einstein had graduated in 1900 with a teaching diploma from the Swiss Federal Institute of Technology, the ETH (after its German-language name), in Zurich, but due to his dubious work ethic and his notorious individualism (he was often absent from lectures), he had offended many people at the Institute. After Einstein’s applications for research positions were unsuccessful, he accepted the position at the patent office, doing work that left him not only enough spare time for research but also peace and isolation from the scientific community. Eventually Einstein found the time to mull over a problem that had been haunting him since he was fifteen years old.2 Within a single year, his annus mirabilis, 1905, Einstein laid the foundation for becoming the most famous physicist of all times, so omnipresent that my mother, when she was a twenty-year-old art student in 1961, could draw him within minutes using only a few brush strokes in a way that made him immediately recognizable (Fig. 13.1).
The puzzle that served as a starting point for Einstein was the question of what a light ray looks like to someone who is moving along with it. Light is an electromagnetic wave, and Einstein wondered why the theory of electromagnetism did not provide an answer to this question. Einstein was put on the right track by, among other things, an eighteen-year-old experiment.3 In 1881 and 1887, Albert Abraham Michelson and Edward Morley had used a spectrometer to measure a possible difference in the speed of light parallel and perpendicular to the earth’s orbit around the sun.
The experiment yielded the astounding result that the speed of light seems to be the same in all directions and regardless of the motion of the earth through a presumed background ether. Einstein’s explanation of this and other related observations was radical, and it followed the thinking of the positivist philosopher Ernst Mach: What can’t be observed does not belong in a scientific theory. If one finds that the speed of light is constant, one thus should use this as starting point for the theory instead of trying to save one’s prejudices with additional assumptions.

Figure 13.1. Einstein, drawn by Frigga Päs. (Courtesy Frigga Päs)

Figure 13.2. Superhero bet. Irrespective of how fast Supergirl chases the light ray, it always escapes her with the same speed of light.
The consequences of this simple principle remind one of a bet entered into by a couple of superheroes (Fig. 13.2). Superman has a flashlight. Supergirl has an enormous amount of energy available and is in perfect physical condition. She bets Superman that she can overtake the light coming from his flashlight. But she is up against Einstein’s principle that the speed of light is the same for all observers. She can’t win. When Superman switches on his flashlight, Supergirl chases the ray as fast as she can. Even if she could race through space at half of the speed of light, the light ray would still recede from her with the same speed as if she were standing still. The reason for this is that the faster Supergirl moves, the more her length scale gets shortened and the slower her clock runs. The result is that light always covers the same (now shrunken) distance in a unit of (now stretched) time. Einstein promoted the speed of light to a benchmark for the determination of time. The stretching of time can be understood if one considers a spaceship in which a certain time interval is defined as the duration a light ray takes to cover a certain distance. A certain fraction of a second, for example, has elapsed once the light ray has been emitted from its source, has hit a mirror, and is reflected back to its origin. Now we assume that the spaceship is moving (Fig. 13.3). For an observer at rest, who sees the spaceship passing by, the light ray, which now also has to keep up with the speed of the spaceship, covers obviously a larger distance. As the speed of light is always the same though, the observer sees time in the moving spaceship going by more slowly than on his wristwatch. This is indeed one of the most astonishing consequences of relativity: Time goes more slowly in moving systems. If the velocity of the spaceship were actually to reach the speed of light, time would freeze. But a massive object such as a spaceship would need infinite energy to get accelerated to the speed of light.

Figure 13.3. Two spaceships, one at rest, the other one moving. In both ships the time span of 12 fractions of a second is defined as the time needed for a light ray emitted from a source to hit a mirror and be reflected back. In the moving spaceship the light covers a larger distance. As the speed of light is always the same, time thus must run slower in the moving spaceship.
But that’s not everything! Within the framework of relativity, two observers moving at different speeds can’t even agree on the chronological order of two events: Whether one event happens before or after another one depends on the observer! To comprehend this, imagine the following encounter in space: While you are drifting in space, your peppy friend Jane hightails by in her spaceship (Fig. 13.4). According to relativity, as long as Jane is neither accelerating nor decelerating each of you has the right to consider yourself at rest and the other one as moving.
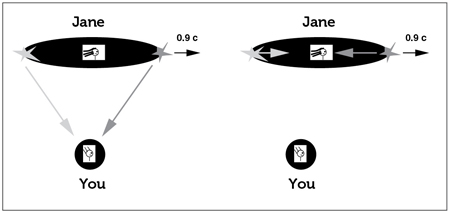
Figure 13.4. Relativity of simultaneity. You see both flashes at the same instant, meaning you conclude that they were set off at the same time. Jane, moving toward the flash at the bow, naturally sees it first and concludes that it was set off before the flash at the stern.
Now Jane sits right in the middle of her spaceship and, in the instant when she passes you, two lights flash: a green one at the bow and a red one at the stern. The red and the green light flashes reach you at the same time, so you conclude that the lights have switched on at the same time. Jane is moving toward the green flash, though. So she sees the green light first. But light has the same speed for anyone, irrespective of whether red or green, and whether it is Jane or you who observes it. The only possible interpretation for Jane is thus that the green light switched on before the red light.
This phenomenon is known as the relativity of simultaneity and has crucial consequences for the understanding of causality in physics: Two observers can disagree on whether two events happen simultaneously or not, and both can be right about it. If you were moving toward the red light while Jane was passing by, then you would have spotted the green flash later than the red flash. That means that a moving observer can perceive two events in reverse order! With this, of course, one question immediately looms large: Can an event happen before its own cause? Can beer be drunk before it was brewed? Can one become tipsy before taking the first sip? Should one decide, then, not to take that sip at all? In special relativity the answer is no, and the reason becomes clear if one considers space-time diagrams and light cones.
A space-time diagram is placed in a coordinate system with space and time axes. It can be used to study the movement through space and time (Fig. 13.5): The horizontal axis describes the position in space, while the vertical axis describes the instant in time, multiplied by the speed of light. Points above the vertical axis have positive time, meaning that this half-plane corresponds to the future. Below the horizontal axis are negative times corresponding to the past, and the origin at the intersections of the axes depicts the here-and-now. Every point in the diagram corresponds to a specific location and a specific time, and every movement corresponds to a line or curve through space-time. If you don’t move at all, for example, you still move through time. Being at rest thus corresponds to movement along the vertical axis. The faster you move through space, the less steep is your resulting movement curve within the space-time diagram. If you could race through space with the speed of light, meaning your ratio of covered distance to elapsed time would be the speed of light, this would correspond to a movement away from the vertical axis at a 45-degree angle. Light rays move along these lines. An even flatter line would correspond to superluminal motion, and thus would be impossible.
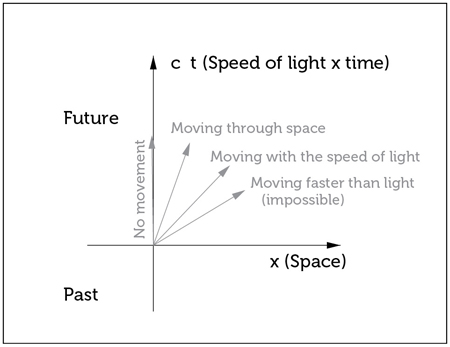
Figure 13.5. Space-time diagram.
The light cone is now the hourglass-shaped figure formed by the 45-degree lines of light rays going from the here-and-now in all directions into the future and coming to the here-and-now from all directions in the past. In the cutaway diagram in the figure, there are four such lines (Fig. 13.6). All space-time points inside the future light cone are reachable in principle, if one just hurries enough. All points in the past light cone could have affected the here-and-now, since from each of these points sufficiently fast travelers or signals could have reached us without exceeding the speed of light. The region outside the light cone, however, is inaccessible for subluminal signals. It can not be reached in the future, and it couldn’t have had any influence on the here-and-now from the past.
So how does the light cone explain why, in special relativity, effects always follow their respective causes, for every observer? The reason is that the sequence of the here-and-now and some arbitrary event can be perceived in reverse order by a moving observer only in the case where this event is situated outside the light cone. And events outside the light cone can neither affect the here-and-now nor be affected by the here-and-now.
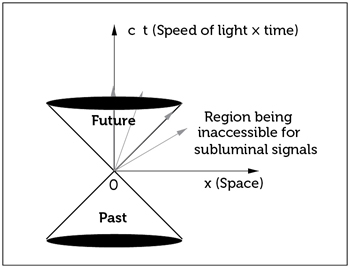
Figure 13.6. Light cone. Inside the cone resides the future, which can be affected by the here-and-now, and the past, which could have influenced the here-and-now. Events from outside the light cone neither affect the here-and-now nor are affected by it.
In summary: Every event that is the cause of an incident in the here-and-now lies in the past or, more accurately, in the past light cone. And every event that could be caused by the here-and-now is situated in the future or, more accurately, in the future light cone. And this remains true for any here-and-now and every observer in the universe. At least in the context of special relativity.
Naturally one asks now: What if? What if you could travel faster than the speed of light? In that case you would arrive outside the light cone, and a moving observer could perceive the order of departure and arrival as reversed:4 she would see you arrive before you departed. And this moving observer could send you, again superluminally, back to your place of origin, where you could arrive before your own departure and meet yourself as you are preparing for your trip (Fig. 13.7). In short: One could travel into the past! But luckily for causality, superluminal travel requires infinite energy, and is thus impossible in special relativity. But then again Einstein was not done at all with his disassembly of space and time.

Figure 13.7. Time travel would be possible if one could move faster than the speed of light (superluminally). (1) Leave the light cone. (2) Move in such a way that departure and arrival get reversed. (3) Return superluminally to the point of origin. Result: you meet yourself before you have started your journey.
It took Einstein eleven years of hard work and many setbacks before he managed to extend his theory of special relativity to general relativity, which now also described gravity. Again Einstein followed the credo of Ernst Mach when he mulled over the question of why mass plays a role in two totally different contexts: as a gravitational mass and as an inertial mass. The inertial mass describes the property of heavy objects to resist being set in motion by an accelerating force: It is easier to push-start a pedal scooter than an SUV. And also more comfortable to be hit by a pedal scooter than by an SUV, at least at the same speed. That means that the inertial mass describes both resistance against acceleration and against deceleration. Gravitational mass is a different concept. It measures how much something weighs, or, more generally, how much it is pulled by gravity. Einstein now argued: If there is no difference between inertial and gravitational mass, then they must be the same thing—whether one carries a mass and thus counteracts gravity or accelerates it and experiences the resistance to acceleration. Or, expressed in a different way: Everything that is not free-falling is being supported somehow. We get a hint of this feeling when an elevator starts to accelerate downward. Free-falling feels like weightlessness, and according to Einstein’s relativity, it is exactly the same. If you let go of an apple while you are in free-fall, you will see that the apple floats next to you. On the other hand, an elevator at rest on earth feels just like an elevator accelerated upward in remote outer space. In both cases a dropped apple will be accelerated toward the elevator’s floor (Fig. 13.8).
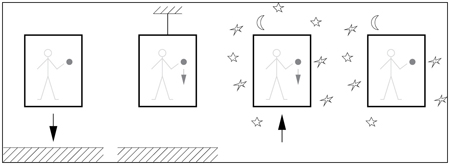
Figure 13.8. The elevator experiment of general relativity. A free-falling elevator in the gravitational field of the earth (left) appears just like one floating weightless in distant space (right), and an elevator at rest in the gravitational field of the earth (center left) appears just like one being accelerated in a weightless environment (center right). Correspondingly, a dropped apple floats (left and right) or gets accelerated toward the elevator floor (center left or center right).
So you can say that gravity itself is not a force, it is only a reflection of accelerating a body out of its natural state of free-fall. You may then well ask why the earth orbits the sun and the moon orbits earth if no force acts on them. Shouldn’t they move along a straight line like a billiard ball on a flat table? Ironically they do exactly that! They follow a straight trajectory, but this trajectory leads around the sun or the earth because space itself is curved. The mass of the central body warps space in such a way that something like a trough in the billiard table is created (see Fig. 13.9).
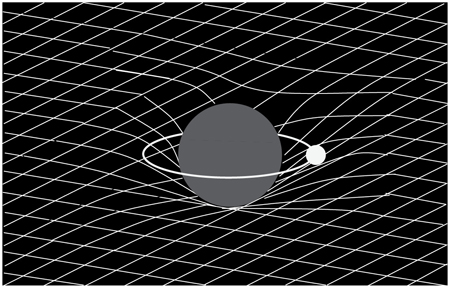
Figure 13.9. In general relativity the motion of the moon around the earth is not the consequence of an attractive gravitational force. Instead, space-time is warped by the earth, and the moon moves along a straight line in curved space. This straight line then goes around the earth.
Einstein’s general relativity leads to jaw-dropping predictions such as the one about black holes, which are corpses of burned-out stars, whose mass got so compressed in their gravitational collapse that inside a certain radius (called the Schwarzschild radius) gravity does not allow even light to escape and time is frozen to a standstill. If an astronaut were to plunge into such a monster, on looking back he would witness the entire history of the universe unwind faster and faster, while his friends left behind on a space station would see him fall more and more slowly into the black hole until his image finally reaches the Schwarzschild radius and freezes. But even if astrophysical observations provide strong hints for the existence of such timeless monsters in relativity, Einstein himself never seriously contemplated that time could ever run backward. Not, that is, until Einstein—who had fled Nazi Germany and found a new home at the Institute for Advanced Study in Princeton—became friends with one of the greatest logicians in history.