© Will Briggs 2021

W. BriggsC++20 for Lazy Programmershttps://doi.org/10.1007/978-1-4842-6306-8_3

3. Numbers

Will Briggs¹  

(1)

Lynchburg, VA, USA

 

Numbers are what make the computer’s world go ‘round, so let’s examine ways to get the computer to handle those numbers for us.

Variables

Variables might seem like the letters we use in algebra – y = mx + b, that sort of thing – but in C++ they’re just places to store values. Example 3-1 shows what it looks like when we create variables.

(Final reminder: As with all numbered examples, you can find Example 3-1 in source code under the appropriate chapter – see Chapter 1’s section “Shapes and the functions that draw them” for how to find and run it.)

int main (int argc, char** argv)

{

    int seasonsOfAmericanIdol                   = 18;

                                     // after a while you lose track

    float hoursIveWatchedAmericanIdol           = 432.5F;

                                     // missed half an episode, dang it

    double howMuchIShouldCareAboutAmericanIdol  = 1.0E-21;

                                     // 1x10 to the -21 power

    double howMuchIDoCareAboutAmericanIdol      = 0.000000000000001;

                                     // So why'd I watch it if I don't care

    sout << "Through " << seasonsOfAmericanIdol << " seasons of American Idol...";

    // ...and some more output...

    // end program

    SSDL_WaitKey();

    return 0;

}

Example 3-1

Variable declarations for my American Idol obsession

This gives us an integer variable; a float variable, which can take decimal places; and two double variables, which can take more decimal places. (How many more depends on the machine you’re on.)

The trailing F on 432.5F means it’s a float, not a double, value. (If you don’t specify, it’s a double.) If you get these confused, you may get a warning from the compiler. To avoid the warning, I use double and forget the F.

1.0E-21 is how C++ writes 1.0 × 10²¹.

You can think of the main function as containing locations with these names, each of which can store a value of the appropriate type (see Figure 3-1).

Figure 3-1

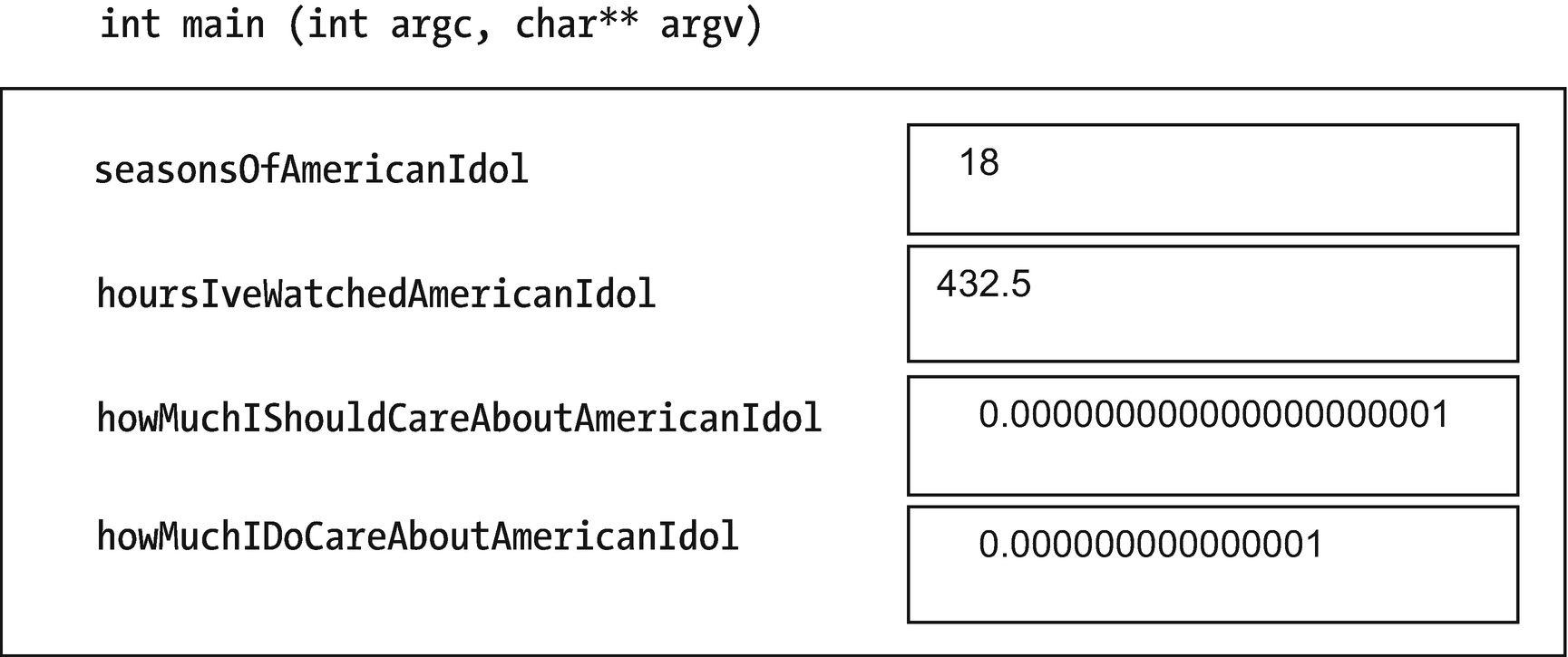
Variables storing values in main

We gave these variables values soon as we made them, on the same line. We didn’t have to, but it’s good practice. It’s disappointing when you find that the number of dollars in your bank account is –68 million, because you didn’t tell the computer what value to initialize it with, and it just happened to start with a very inappropriate number.

Golden Rule of Variables

Initialize them.

It’s also good to make descriptive names like the preceding ones. It’s frustrating to search through code trying to find out what "z" or "x" means. But you know exactly what seasonsOfAmericanIdol means.

Variable names start with letters (possibly preceded with _’s), but after that they can have numerals in them. Capitalization matters: temp and Temp are different variables.

Extra

Variable and constant names should be descriptive and shouldn’t be the same as any of the built-in keywords in C++ (const, int, void, etc.).

By convention, C++ constants are written in ALL CAPS to SCREAM at the programmer that this is a CONSTANT, not a variable, value. To separate words jammed together, use _: MAX_LENGTH, for example.

Conventions for variable names are flexible. I use “camel case” variables: you jam words together to make a variable, capitalize all first letters of words except for the first – firstEntry, minXValue. I reserve initial capitals for created types like SSDL_Image. Initial _’’s are for the compiler’s own identifiers. There are other conventions; whatever convention you use, it’s best to be clear as possible.

How do you think it got its name?

Constants

We’ve already made some constants:

const SSDL_Color MAHOGANY   = SSDL_CreateColor    (192,  64,   0);

const SSDL_Font  FONT       = SSDL_OpenSystemFont ("timesbd", 24);

Now please consider these two simpler constant declarations:

constexpr double PI               = 3.14159265359;

constexpr int    DAYS_PER_FORTNIGHT = 7+7;  // A fortnight is two weeks, so...

What’s the difference? const simply means “does not change.” constexpr means “does not change and gets set at compile time.” The latter makes programs a little faster. We won’t notice with the preceding declarations, but as programs get bigger and more complex, it may matter more. (I can’t do it with SSDL_CreateColor or SSDL_OpenSystemFont, because those won’t work till SDL is started at runtime.)

I use constexpr when the initial value is just numbers (like 3.14159265359 or 7+7) and const when it’s a function call (like SSDL_OpenSystemFont ("times", 18)). Eventually we’ll refine that (see Chapter 26), but it’s good for now.

When to use constants, not literal values

When should I use a literal value, like 100, and when should I use a constant symbol, like CENTURY? The answer is almost always: use the constant rather than the bare literal value. There are two reasons:

One is to be clear, as shown earlier. You’re going back through a program, and you see a reference to 7. Seven what? Days in the week? The number of deadly sins? The age you were when you wrote your very first program? You’ll have to do detective work to figure it out, especially if there’s more than one 7 in your program. Detective work is not for the lazy. Better to document it with a clear name.

The other reason is to easily change the value. For example, there are by convention seven deadly sins, but using bare numeric literals like 7 is a pretty deadly sin in programmer terms. So maybe that constexpr int NUMBER_OF_DEADLY_SINS = 7; needs to be updated to 8. If you used this constant, you’ve got one line to change. If you put 7 all through your program, you’ll have to go through figuring which 7’s to change and which ones to leave alone. Detective work again.

The bottom line is clarity. We won’t go back to the bug face program in Chapter 1 and replace all those numbers with constexprs, because it would make the program harder to follow; each value is unique, and naming it doesn’t make it clearer. (We have comments to show what it means anyway.) But the bug face program is the exception. Generally, values should be named.

Golden Rule of Constants

Any time it’s not blindingly obvious what a numeric literal value is for, define it as a constant symbol, in ALL CAPS, and use that name whenever you refer to it.

Extra: Adding

constexpr to the Bug’s-Head Program

Yes, I concede – grudgingly – that the bare numeric literals in Chapter 1’s bug’s-head program can stay, for reasons given earlier. But what if we refer to values more than once? Use them to calculate positions of parts of the face? In such a case, we need constants. So

// draw the bug's head

SSDL_RenderDrawCircle (430, 260, 200);

// left eye, and right

SSDL_RenderDrawCircle (430-80, 260, 50);

SSDL_RenderDrawCircle (430+80, 260, 50);

would become

constexpr int HEAD_X     = 430, HEAD_Y   = 260, HEAD_RADIUS = 200;

constexpr int EYE_RADIUS =  50;

constexpr int EYE_OFFSET =  80; // How far lt/rt an eye is from center

// draw the bug's head

SSDL_RenderDrawCircle (HEAD_X,            HEAD_Y, HEAD_RADIUS);

// left eye, and right

SSDL_RenderDrawCircle (HEAD_X-EYE_OFFSET, HEAD_Y, EYE_RADIUS);

SSDL_RenderDrawCircle (HEAD_X+EYE_OFFSET, HEAD_Y, EYE_RADIUS);

Sure, it’s longer now – but it’s gone from “How do these numbers relate to each other? Why do 430 and 260 keep showing up?” to a built-in explanation. Nice. (The full program is in source code in ch3 as bugsHead-with-constexpr; run it with make as usual (g++) or through ch3.sln (Visual Studio). The output is in Figure 3-2.)

Figure 3-2

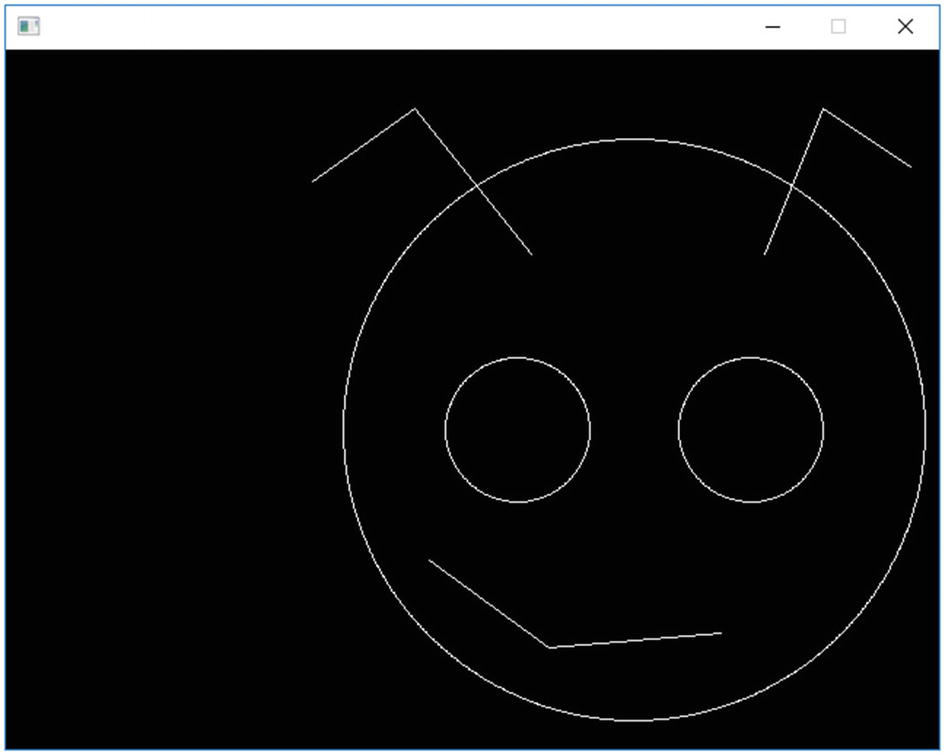
A bug’s head, drawn using constants and calculations

Math operators

Table 3-1 contains the arithmetic operators you can use in C++. They’re used as you might expect: 2.6+0.4 or alpha/beta or -2*(5+3).

Table 3-1

The arithmetic operators

Operator	Meaning
+	Addition
-	Subtraction, negation
*	Multiplication
/	Division
%	Modulus

Integer division

Back before you learned fractions, when you only used whole numbers, the result was always a whole number: 5 divided by 2 was 2, with a remainder of 1. It’s the same for C++’s integer division: 5/2 gives you another integer, 2, not 2.5 – that’s a floating-point value.

This can be confusing. 1/2 sure looks like it should be 0.5, but since 1 and 2 are integers, 1/2 has to be an integer too: 0.

In keeping with the way we divide integers, C++ also provides % , the modulus operator, which means “divide and take the remainder.” 5%2 gives us 1, the remainder after dividing 5 by 2. We’ll see more of % in Chapter 8, in section “Random numbers.”

Assignment (=) operators

We’ve been using = already :

const SSDL_Color MAHOGANY   = SSDL_CreateColor  (192,  64,   0);

int   seasonsOfAmericanIdol = 18;

Constants can’t be changed past that first line, or they wouldn’t be constant, but variables can vary whenever you like:

x = 5; y = 10;

x = 10;             // I changed my mind: put a 10 in X, replacing the 5

seasonsOfAmericanIdol = seasonsOfAmericanIdol + 1; // Another year! Yay!

The latter means take whatever number is in that seasonsOfAmericanIdol memory location, add 1 to it, and put the resulting value back into that same place.

It can also be written this way: seasonsOfAmericanIdol + = 1;.

They mean the same thing: add 1 to seasonsOfAmericanIdol.¹

It works for other arithmetic operators: -=, *=, /=, and %= are all defined the same way.

A diving board example

Now let’s put this into practice with a program that uses math for sport. Someone’s going off the diving board. We’ll make second-by-second images of the character as it plunges toward the water (Example 3-2).

// Program to draw the path of a diver

//              -- from _C++20 for Lazy Programmers_

#include "SSDL.h"

int main(int argc, char** argv)

{

    SSDL_SetWindowTitle("Sploosh!  Hit a key to end");

    // Stuff about the board

    constexpr int BOARD_WIDTH        = 60,²

                  BOARD_THICKNESS    =  8,

                  BOARD_INIT_Y       = 20;

    SSDL_RenderDrawRect(0, BOARD_INIT_Y,

                        BOARD_WIDTH, BOARD_THICKNESS);

    // ...the water

    constexpr int SKY_HEIGHT         = 440;

    SSDL_SetRenderDrawColor(BLUE);

    SSDL_RenderFillRect(0, SKY_HEIGHT,

                        SSDL_GetWindowWidth(),

                        SSDL_GetWindowHeight() - SKY_HEIGHT);

                                  // height is window height - sky height

    // ...the diver

    constexpr int

        WIDTH              = 10, // Dimensions of "diver"

        HEIGHT             = 20,

        DISTANCE_TO_TRAVEL = 20, // How far to go right each time

        FACTOR_TO_INCREASE =  2; // Increase Y this much each time

    constexpr int INIT_X   = 50,

                  INIT_Y   = 10;

    int                x   = INIT_X; // Move diver to end of board

    int                y   = INIT_Y; // and just on top of it

    const SSDL_Color DIVER_COLOR = SSDL_CreateColor(200, 150, 90);

    SSDL_SetRenderDrawColor(DIVER_COLOR);

    // Now draw several images, going down as if falling, and right

    // Remember x+=DISTANCE_TO_TRAVEL means x=x+DISTANCE_TO_TRAVEL

    //   ...and so on

    SSDL_RenderFillRect(x, y, WIDTH, HEIGHT);

    x += DISTANCE_TO_TRAVEL;  // go right the same amount each time,

    y *= FACTOR_TO_INCREASE;  //  down by an ever-increasing amount

    SSDL_Delay(100);          // 100 ms -- 0.1 seconds

    // Same thing repeated several times

    SSDL_RenderFillRect(x, y, WIDTH, HEIGHT);

    x += DISTANCE_TO_TRAVEL; y *= FACTOR_TO_INCREASE;

    SSDL_Delay(100);          // 100 ms -- 0.1 seconds

    SSDL_RenderFillRect(x, y, WIDTH, HEIGHT);

    x += DISTANCE_TO_TRAVEL; y *= FACTOR_TO_INCREASE;

    SSDL_Delay(100);          // 100 ms -- 0.1 seconds

    SSDL_RenderFillRect(x, y, WIDTH, HEIGHT);

    x += DISTANCE_TO_TRAVEL; y *= FACTOR_TO_INCREASE;

    SSDL_Delay(100);          // 100 ms -- 0.1 seconds

    SSDL_RenderFillRect(x, y, WIDTH, HEIGHT);

    x += DISTANCE_TO_TRAVEL; y *= FACTOR_TO_INCREASE;

    SSDL_Delay(100);          // 100 ms -- 0.1 seconds

    SSDL_RenderFillRect(x, y, WIDTH, HEIGHT);

    x += DISTANCE_TO_TRAVEL; y *= FACTOR_TO_INCREASE;

    SSDL_Delay(100);          // 100 ms -- 0.1 seconds

    // end program

    SSDL_WaitKey();

    return 0;

}

Example 3-2

A program to show a diver’s path, using constexprs and math operators

Things to notice:

• I initialize all variables, as always.

• There are no bare numeric literals in any calculation or variable initialization; it’s CONSTANT values all the way.

• I repeat the same pair of lines six times. Seriously? Is that lazy? We’ll have a better way in Chapter 5.

Figure 3-3 is the result.

Figure 3-3

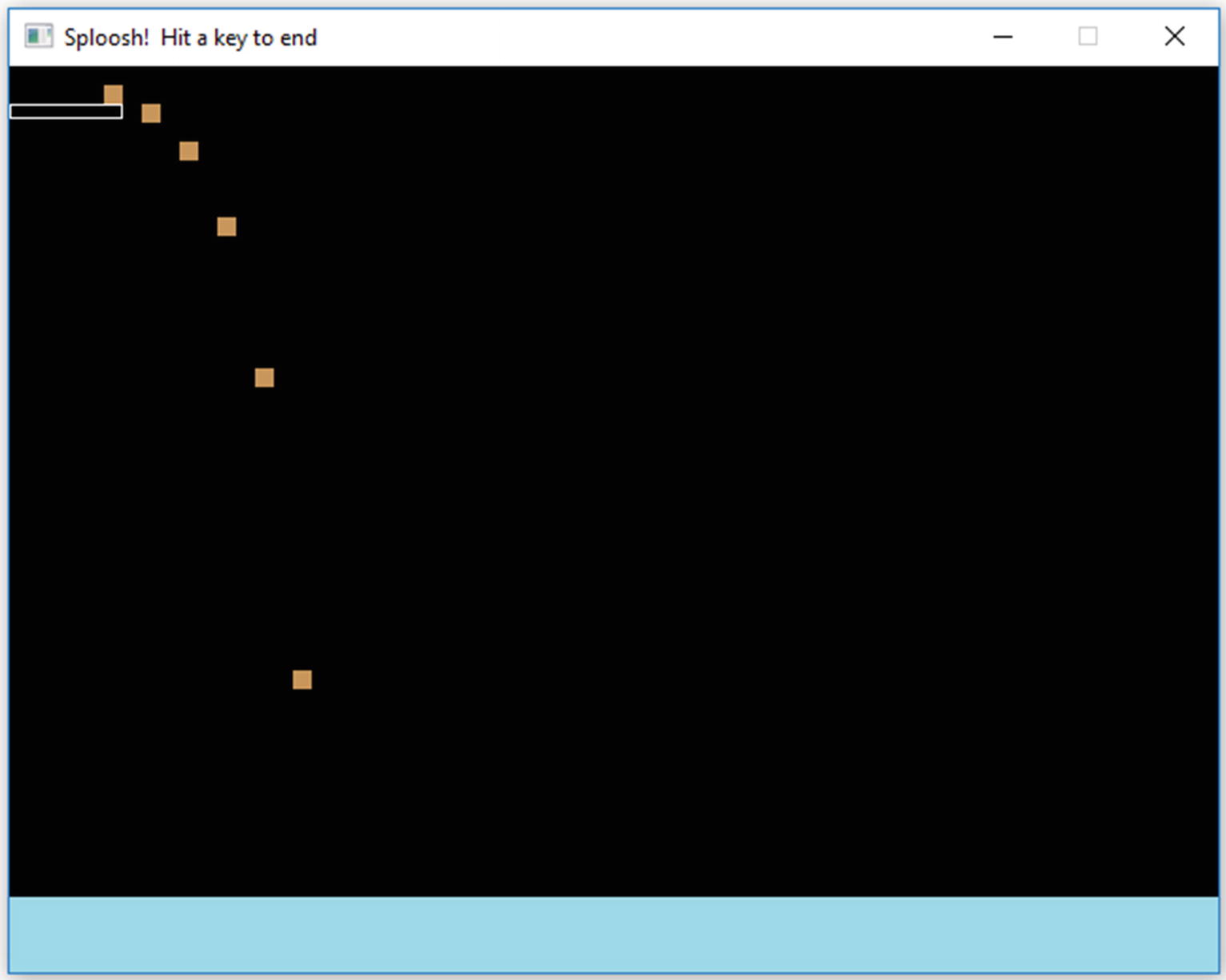
A program that shows the path of a diver into the water

That worked, and in some small sense evokes the terror I feel when I go off the high dive.

The no-worries list for math operators

Here are some things C++ will handle naturally enough you won’t need to memorize anything for them:

• Precedence : Consider a math expression, 2*5+3. In C++, as in an algebra class, we’d do the multiplying before the adding; this means (2*5)+3 = 13, not 2*(5+3) = 16. Similarly, in 8/2-1, we divide before subtracting. In general, do it the way that makes sense to you, and it’ll be right. If not, use parentheses to force it to go your way: 8/(2-1).

• Associativity: In 27/3/3, which division comes first? Is it done like 27/(3/3), or (27/3)/3? Arithmetic operations are performed left to right. Assignment is done right to left: x=5+2 requires you to evaluate the 5+2 before doing anything to the x.

Precise details of precedence and associativity are in Appendix B.

• Coercion : If you want to cram a variable of one type into another, C++ will do it:

double Nothing = 0;  // Nothing becomes 0.0, not 0

int Something = 2.7; // ints can't have decimal places , so

                     // C++ throws away the .7;

                     // Something becomes 2. No rounding, alas

If you mix integers and floating-point numbers in a calculation, the result will be the version with the most information, that is, floating point. 10/2.0, for example, gives you 5.0.

Exercises

1. 1.

   Using constants for centimeters per inch (2.54) and inches per foot (12), convert someone’s height from feet and inches to centimeters, and report the result.

    
2. 2.

   Now do the reverse: centimeters to feet and inches.

    
3. 3.
   Accumulate this sum for as far as you’re willing to take it, 1/2 + 1/4 + 1/8 + 1/16 +…, using +=. Do you think if you did it forever you would reach a particular number? Or would it just keep getting bigger? The ancient philosopher Zeno of Elea would have an opinion on that (https://en.wikipedia.org/wiki/Zeno%27s_paradoxes, at time of writing). But he’d be wrong.

   

   You can’t get there from here. —Zeno. Sort of.

    
4. 4.

   Make a program to have a box move across the screen in 0.1-second jumps – like the diver moving, but clearing the screen at every jump so it looks like it’s really moving. Maybe make the delay shorter for a better illusion of motion.

    

Built-in functions and casting

Now I want to make a geometric figure, a five-point star. But forget Chapter 1’s graph paper. I want the computer to figure it out for me. Let it do its own (virtual) graph paper.

If I think of the star as inscribed in a circle…I probably know the center, so what I need calculated is the points at the edges. Each point is one-fifth of the way further around the circle than the previous, so if a circle is 360 degrees, the angle between them is 360/5 degrees. If you use radians rather than degrees, like C++, that’s 2π/5 radians between the points.

SDL uses x, y coordinates, so we’ll need a way to get that from the angle. We can do that using the picture in Figure 3-4. Since sine of the angle θ is the y distance divided by radius (if math isn’t your thing, trust me), the y distance is RADIUS * sin (θ). Similarly, the x distance is RADIUS * cos (θ).

Figure 3-4

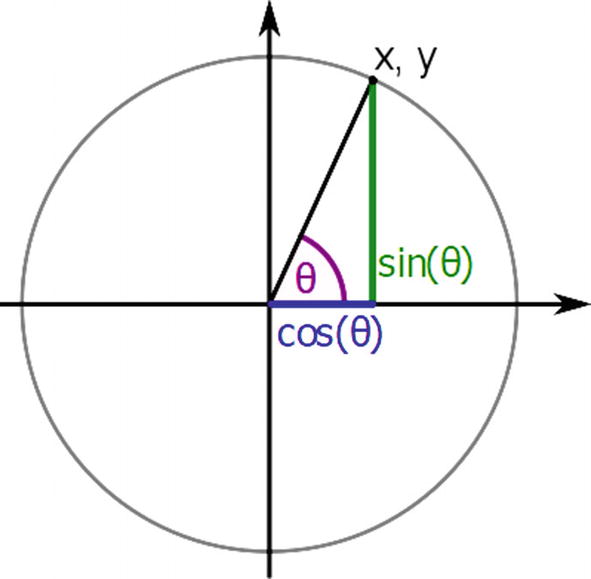
Sine and cosine as related to x and y

The sin and cos functions , like most C++ math functions, have their declarations in an include file called cmath,³ added to our program. Thus

#include <cmath>  // System include files (those that come with the compiler)

                 // have <>'s not ""'s.

#include "SSDL.h"

This program is meant to draw a line from center to edge, turn one-fifth of the way around the circle and do it again, and keep going for a total of five lines.

// Program to make a 5-point star in center of screen

//              -- from _C++20 for Lazy Programmers_

#include <cmath>

#include "SSDL.h"

int main(int argc, char** argv)

{

    constexpr double PI = 3.14159;

    // Starting out with some generally useful numbers...

    // center of screen

    const     int CENTER_X           = SSDL_GetWindowWidth () / 2,

                  CENTER_Y           = SSDL_GetWindowHeight() / 2;

    constexpr int RADIUS             = 200,

                  NUMBER_OF_POINTS   =   5;

    // angle information...

    double    angle                  = 0;     // angle starts at 0

    constexpr double ANGLE_INCREMENT = (2 / NUMBER_OF_POINTS) * PI;

                            // increases by whole circle/5 each time

    // ...now we make the successive lines

    int x, y;               // endpt of line (other endpt is center)

    x = CENTER_X + int(RADIUS * cos(angle));       // calc endpoint

    y = CENTER_Y + int(RADIUS * sin(angle));

    SSDL_RenderDrawLine(CENTER_X, CENTER_Y, x, y); // draw line

    angle += ANGLE_INCREMENT;                      // go on to next

    x = CENTER_X + int(RADIUS * cos(angle));       // calc endpoint

    y = CENTER_Y + int(RADIUS * sin(angle));

    SSDL_RenderDrawLine(CENTER_X, CENTER_Y, x, y); // draw line

    angle += ANGLE_INCREMENT;                      // go on to next

    x = CENTER_X + int(RADIUS * cos(angle));       // calc endpoint

    y = CENTER_Y + int(RADIUS * sin(angle));

    SSDL_RenderDrawLine(CENTER_X, CENTER_Y, x, y); // draw line

    angle += ANGLE_INCREMENT;                      // go on to next

    x = CENTER_X + int(RADIUS * cos(angle));       // calc endpoint

    y = CENTER_Y + int(RADIUS * sin(angle));

    SSDL_RenderDrawLine(CENTER_X, CENTER_Y, x, y); // draw line

    angle += ANGLE_INCREMENT;                      // go on to next

    x = CENTER_X + int(RADIUS * cos(angle));       // calc endpoint

    y = CENTER_Y + int(RADIUS * sin(angle));

    SSDL_RenderDrawLine(CENTER_X, CENTER_Y, x, y); // draw line

    angle += ANGLE_INCREMENT;                      // go on to next

    // end program

    SSDL_WaitKey();

    return 0;

}

Example 3-3

A star using sin and cos functions

Figure 3-5 shows the result. What?

Figure 3-5

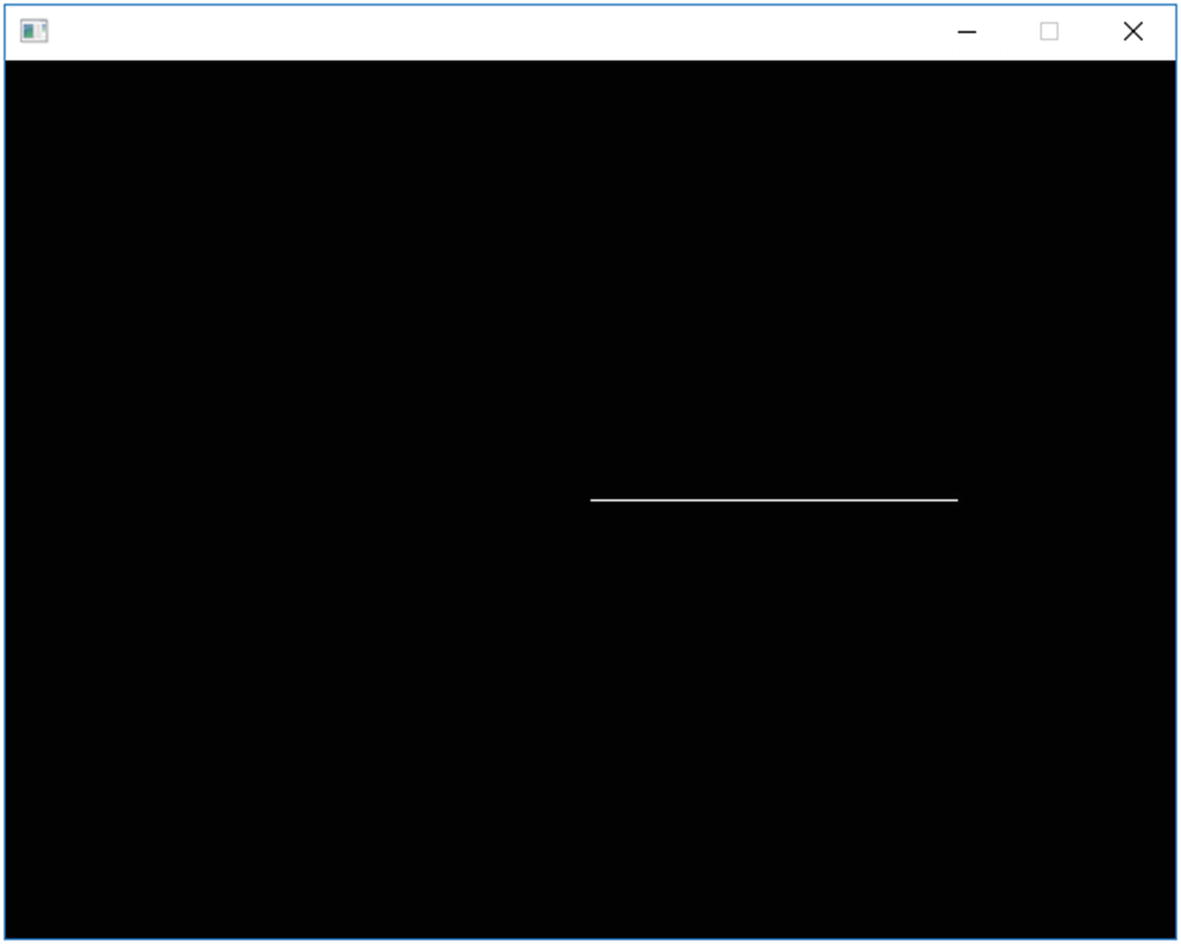
A five-point star – at least, it was supposed to be

This will be a breeze to debug once we’ve covered the debugger in Chapter 9, but for now, we’ll just have to channel Sherlock Holmes. That line never changes, which means angle never changes, which must mean ANGLE_INCREMENT is 0. Why would it be 0?

Look at that calculation: ANGLE_INCREMENT = (2/NUMBER_OF_POINTS)*PI. The first thing to do is divide 2 by NUMBER_OF_POINTS, or 5. Since both are integers, we do integer division: 5 goes into 2 zero time (with a remainder of 2, for what it’s worth), so 2/5 gives us zero. Zero times PI is zero. So ANGLE_INCREMENT is zero.

We needed floating-point division.

One way is to force 2 and 5 to be float or double. You can do this by saying.

double (whatEverYouWantToBeDouble).

This is called casting.

double (2/NUMBER_OF_POINTS) won’t work because that divides 2 by 5, gets 0, and converts the 0 to 0.0. It’s still doing integer division.

Any of the following will work. As long as one of the arguments of / is double or float, you’ll get a result with decimal places:

double (2)/NUMBER_OF_POINTS

2/double (NUMBER_OF_POINTS)

2.0 / NUMBER_OF_POINTS

So changing the beginning of main to what you see in Example 3-4 repairs the problem.

int main(int argc, char** argv)

{

...

    // angle information...

    double        angle = 0;  // angle starts at 0

    constexpr double ANGLE_INCREMENT

               = (2 / double (NUMBER_OF_POINTS)) * PI;

                              // increases by whole circle/5 each time

    ...

Example 3-4

A new beginning to main, to make Example 3-3 work

Figure 3-6 shows the result.

Figure 3-6

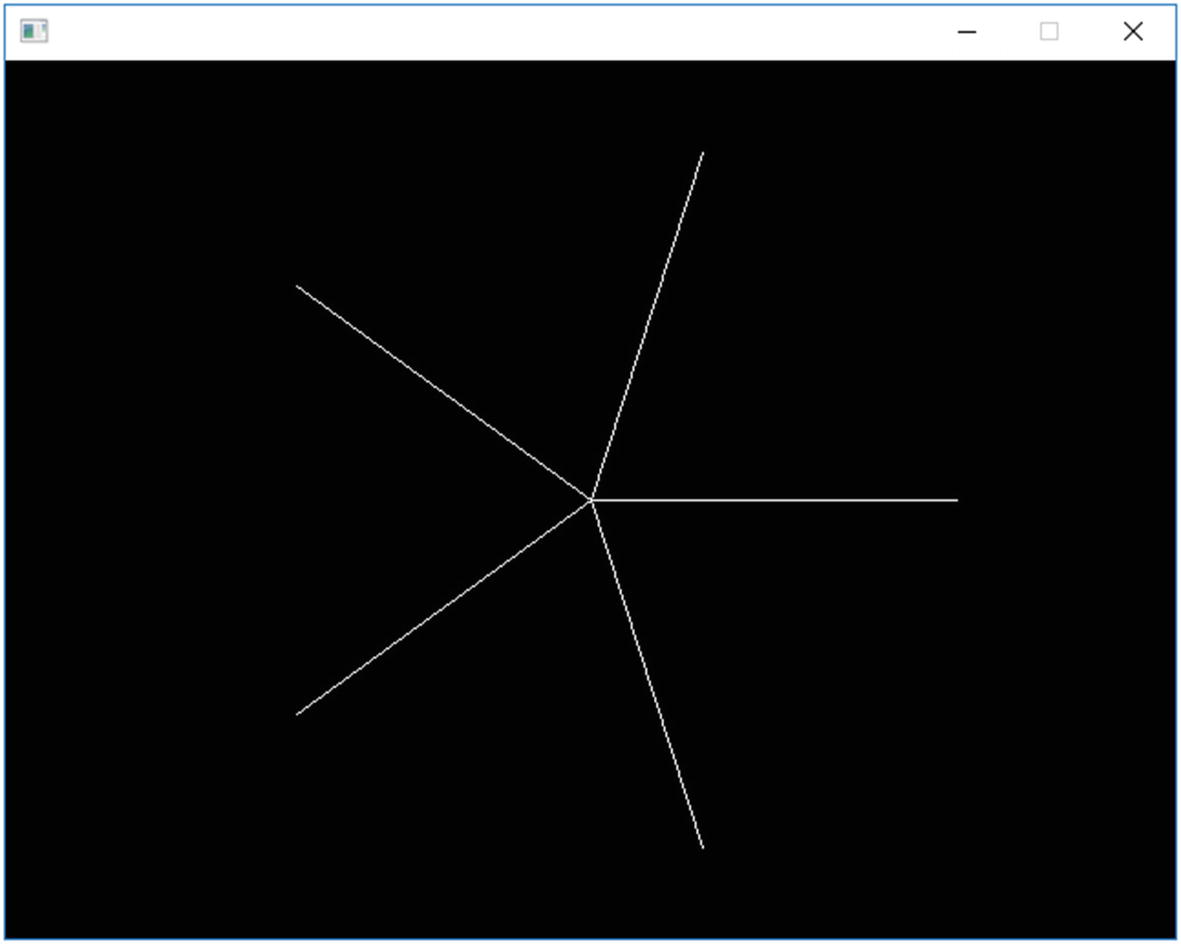
A five-point star

It’s not vertical, it seems. Exercise 1 is about turning it straight.

Other commonly useful mathematical functions include asin and acos (reverse sine and cosine), pow (raising a number to a power), abs (absolute value), and sqrt (square root). See Appendix F for more.

Antibugging

• You call a value-returning function, but it has no effect. Here’s an example with a function we saw earlier:

  // Center "Blastoff!" on the screen

  SSDL_GetScreenWidth();

  SSDL_RenderTextCentered (320, 240, "Blastoff!");

  Sure, you called SSDL_GetWindowWidth()…but you never did anything with the result! C++ is happy to let you waste time by calling functions and not using what they give you. (It’s sort of a “let the programmer shoot self in the foot, and laugh” language.) If you want to use the value, refer to it wherever you want that value:

  SSDL_RenderTextCentered(SSDL_GetScreenWidth ()/2,

                          SSDL_GetScreenHeight()/2,

                          "Blastoff!");

  Or put it in a variable or constant for later use:

  const int SCREEN_WIDTH  = SSDL_GetScreenWidth ();

  const int SCREEN_HEIGHT = SSDL_GetScreenHeight();

  SSDL_RenderTextCentered (SCREEN_WIDTH/2, SCREEN_HEIGHT/2, "Blastoff!");

• You divided two integers to get a floating-point number between zero and one, but you got zero. See Example 3-3 in this section. One of those operands of the / symbol should be cast to float or double.

• You get a warning about conversion between types. You can ignore it, but to make it go away, cast the offending item to what you wanted. Then the compiler will know it was intentional.

Exercises

1. 1.

   Adjust the star in Example 3-4 so that the star’s top point is straight up.

    
2. 2.

   Make a clock face: a circle with numbers 1–12 in appropriate places.

    
3. 3.

   (Harder) Here’s how to get system time in seconds:

   #include <ctime >

   ...

   int timeInSeconds = int⁴ (time (nullptr));

   Use % and / operators to find the current time in hours, minutes, and seconds. The hours may be off due to what time zone you’re in; you can adjust appropriately.

    
4. 4.

   Having done 2 and 3, make a clock face that shows the current time.

    

Footnotes

1

If you want to add 1, rather than some other number, there’s a special “increment” operator just for that:

++seasonsOfAmericanIdol;

We’ll see that again in Chapter 5, along with “decrement” (--).

 

2

All these =’s lined up so precisely. Is this overkill? Look how easy it is to find all my variables and their values! Another good habit to get into.

 

3

Include files inherited from C++’s ancestor C start with “c”: cmath and cstdlib, for example.

 

4

We cast to int to avoid that conversion warning mentioned in “Antibugging.” The time function returns a time_t (whatever that is); we’ll force it to be an int.