W. BriggsC++20 for Lazy Programmershttps://doi.org/10.1007/978-1-4842-6306-8_6

6. Algorithms and the Development Process

Will Briggs¹

(1)

Lynchburg, VA, USA

Let’s step back from the details of C++ and think about something in the big picture: specifically, the need for thinking about the big picture. In the rest of life, doesn’t planning help? You wouldn’t build a house, or cook a meal, without a plan. (Heating soup in the microwave doesn’t count.)

In programming, the plan is called an algorithm: a sequence of steps, to be executed in order, that leads to a goal.

Adventures in robotic cooking

Imagine if we can get our computer to make biscuits (the fluffy kind – like scones, but not sweet). A computer can follow instructions, but they must be clear.

I get out a bowl, and…what goes in biscuits, anyway? You got me. Flour should help. Don’t they put eggs in biscuits? And milk? Tell the robot to dump some flour in a bowl, put in a couple of eggs and a glug of milk, mix it up hard as it can, roll them, and put them in the oven.

They’ll come out hard as bricks, of course. Our robo-chef put eggs in – my grandmother would laugh at that – and mixed them way too much. I should have made a solid plan first.

../images/477913_2_En_6_Chapter/477913_2_En_6_Fig1_HTML.jpg — (Left) Biscuits improperly made are often of use to the construction industry. At least you’ll think so once you try to eat them. (Right) What I’m hoping to make instead

Tip

Write the algorithm before the program, even for simple tasks.

Exactly what should I have told it to do? Here’s one option:

1 cup/250 mL all-purpose flour

1/2 tsp/3 mL salt

1/8 cup/30 mL cold shortening

1/3 cup/80 mL milk

Heat oven to 450° F/ 230° C

Mix dry ingredients

Mix in shortening just till it's distributed

Mix in milk

Form into balls

Bake in the oven

Oven heated? Check. The robot can mix the dry ingredients. Let it take a cup of flour and mix in the salt and baking soda. The cup will overflow as the robot mixes them. Why didn’t it put the flour into a bowl? I didn’t tell it to.

Next, it will mix in the shortening and then the milk. Of course, we’ll get a wet mess. Then it will form the mess into balls. How many? I didn’t say. Is two OK? Then it puts the seeping mess in the oven, at which point it falls through the rack onto the bottom… I didn’t tell it to use a tray, either. And I never told it to take the biscuits out! Got a fire extinguisher handy?

The steps weren’t specific enough. For example, I told it to mix, but didn’t tell it that one of the steps in that is to put things into a bowl. We need more detail. Stepwise refinement is how to solve that problem: write down what needs doing, then break that step into sub-steps, then break those into sub-steps, until the steps so simple even a computer can handle them.

Tip

Refine your algorithm till it’s obvious how each line converts to C++.

Let’s try again:

1 cup/250 mL all-purpose flour

1/2 tsp/3 mL salt

1/8 cup/30 mL cold shortening

1/3 cup/80 mL milk

Heat oven to 450° F/ 230° C

Mix dry ingredients:

Put dry ingredients into a large bowl

Mix them

Mix in shortening just till it's distributed:

Cut shortening into small bits (half-centimeter sized)

Put shortening into the large bowl

Mix just till it's distributed

Mix in milk:

Put milk into the large bowl

Mix till it's distributed

Form into balls:

Get a cookie sheet

While there is dough left

Put flour on your hands so the dough won't stick

Take out dough the size of a baby's fist

Put it on the cookie sheet, not touching any others

Bake in the oven:

Put the cookie sheet in the oven

Wait till the biscuits are golden brown on top

Take the cookie sheet and biscuits out

Good. Now we’re done. It’s a tediously detailed algorithm, but if we’re going to get a computer to understand, we have to break it down till it’s obvious – to a computer! – what the steps mean.

Is it time-consuming to write all that detail? Not as time-consuming as puzzling out the same detail while writing code, getting it wrong, debugging, and starting again and again. Experts agree time spent planning ahead reduces programming time spent overall. For that reason, lazy programmers use the following rule:

Golden Rule of Algorithms

Always write them.

Extra

Lady Ada Lovelace (1815–1852) and Charles Babbage (1791–1871) are credited with being the world’s first computer scientists. Too bad computers hadn’t been invented yet.

../images/477913_2_En_6_Chapter/477913_2_En_6_Fig2_HTML.jpg — Charles Babbage, Lady Ada Lovelace

Babbage certainly tried. He got the British government to fund his Difference Engine, which was meant to be a mechanical calculator, and then his Analytical Engine, designed as a mechanical computer. (In those days, government funding of research was nearly unheard of. Maybe that’s why it was called “the Age of Invention.”) Machine parts weren’t of sufficient refinement at the time, and the project failed.

Lovelace, daughter of the poet Lord Byron, took an interest in Babbage’s machine and understood the nature of the programs it ran or, rather, would have run if it had existed. “The Analytical Engine has no pretensions whatever to originate anything,” she said. “It can do whatever we know how to order it to perform.” This is sometimes used as an objection to the concept of artificial intelligence.

Writing a program, from start to finish

Let’s apply this planning-ahead thing to a real, if small, programming task.

Here are the steps we might go through to create the program for some goal:

Identify requirements, that is, make a precise statement of the goal.
Write the algorithm.
Trace the algorithm by hand.
Convert the algorithm to valid C++ code.
Compile.
Test.

If there are errors along the way, we can go back to previous steps.

Requirements: What do we want to do?

I want to make a series of concentric circles such that each circle is half the area of the one outside it (Figure 6-1). We’ll keep going till they start to blur (maybe when the radius is around 1 pixel). The outer circle’s radius is, oh, 200.

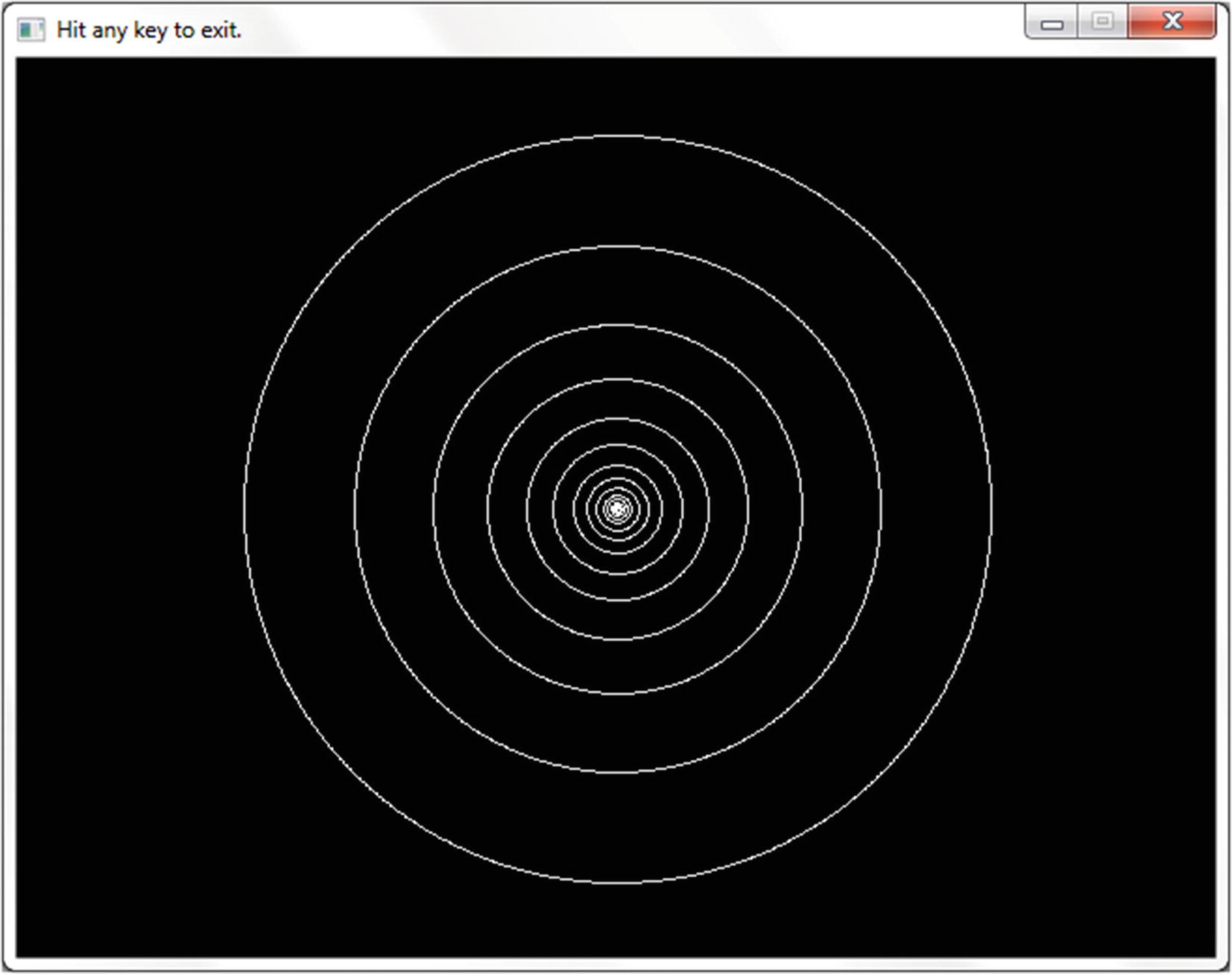
../images/477913_2_En_6_Chapter/477913_2_En_6_Fig3_HTML.jpg — Figure 6-1
A program that makes concentric circles, each half the area of the next bigger one

Ready to start coding? Not yet. First, we’ll make a plan, as discussed in the previous section.

Algorithm: How do we do it?

So what should happen at runtime?

draw the first circle

draw the second

keep going until the circle's too small to see -- radius 1, I'd suppose

Too obvious? I find that programming goes much more easily when I state the obvious, write it down, and try to refine it.

Tip

State the obvious, especially when just starting.

It’s not specific enough yet. We don’t know how to draw the circles because we don’t know the radii.

The outermost circle’s is 200. The next one in, as previously stated, I want the area to be half that of the first. Remember the formula for the area of a circle: π radius². To get a halved area, we’ll need next circle’s area = first circle’s area/2. This works out to be that the next radius is the first radius/ $\sqrt{2}$ .

Here’s the amended algorithm:

draw the first circle, with radius 200...

No, I didn’t say where! Try again:

draw the first circle at center of screen, with radius 200

draw the second circle at center of screen, with radius 200 / √2

draw the third circle at center of screen, with radius 200 / √2 / √2...

Too complicated.

We could use variables. We’ll start the value for radius at 200 and change it every time:

start radius at 200

draw a circle at center of screen, with this radius

divide radius by √2 to get a circle with half the area as before

keep going until the circle's too small to see -- radius 1, I'd suppose

That “keep going” sounds like we need a loop. We don’t know how many times we’ll do it, but it’s at least once, so by the Golden Rule of Loops, it’s a do-while:

start radius at 200

draw a circle at center of screen, with this radius

divide radius by √2

while radius > 1 (quit when circle's too small to see)

This is specific enough. Do you need to go to this trouble every time you write a program? Pretty much. As time goes by and your skills improve, you can specify less detail. But experts still write out steps for anything they’re not certain of.

Trace the algorithm: Will it work?

Another thing I do is trace through the algorithm by hand, seeing what it does, and confirm that it does what I want.

First, radius is set to 200. The area is π 200². We draw a circle with that radius.

Next, radius is set to what it was divided by $\sqrt{2}$ . The area is π (200/ $\sqrt{2}$ )² = π 200²/2, which is half the first area; that’s what I wanted. We draw the new circle.

Next, radius is set to what it became divided by $\sqrt{2}$ . The area is π (200/ $\sqrt{2}/\sqrt{2}$ )² = π 200²/4, which is one-fourth the first area. Good. We draw the new circle.

Seems OK.

As programs get more complex, reviewing your algorithms will be even more useful. Why spend time getting a program to compile, if it’s not going to do what we want? I’m too lazy for that.

Coding: Putting it all into C++ (plus: commenting the lazy way)

To create the program, I start the usual way : I tell the reader exactly what I’m doing at the top of the file. Then I put the algorithm right into main, as comments, so I can refine it into a working program.

There’s no point compiling until the code is written as, well, code. So I’ll refine it over the next few pages until I get something that looks like it’ll work:

// Program to draw 5 concentric circles

// Each circle is twice the area of the one inside it

// -- from _C++20 for Lazy Programmers_

#include "SSDL.h"

int main (int argc, char** argv)

{

// start radius at 200

// do

// draw a circle at center of screen, with this radius

// divide radius by sqrt (2)

// while radius > 1 (quit when circle's too small to see)

return 0;

}

The cops didn’t arrest me for putting the algorithm right there into the editor, so I guess I’ll keep going.

Tip

Include the algorithm in the program, after //’s, and you’ve already written most of your comments.

The editor can turn text into comments quickly. (This is also useful for making troublesome bits of code stop generating errors; put ‘em in comments – “comment them out” – till you’re ready to deal with them.)

emacs

: Highlight the region and select C++ ➤ Comment out region to comment it; press Tab to indent if needed. If you’re in a non-graphical version of emacs, highlight the region by pressing Ctrl-Space at one end of the region and then moving the cursor to the other end. Ctrl-C will turn it into comments, and Tab will indent.

(Note that final cool emacs tip too: Highlight a region and press Tab, and emacs indents the region all at once.)

Visual Studio

: Clicking the Comment out button will turn highlighted code into comments. (It looks like parallel horizontal lines and is highlighted at the top right of Figure 6-2.)

../images/477913_2_En_6_Chapter/477913_2_En_6_Fig4_HTML.jpg — Figure 6-2
The Visual Studio window, with the Comment out button highlighted (top right)

Figure 6-3 shows the commenting.

../images/477913_2_En_6_Chapter/477913_2_En_6_Fig5_HTML.jpg — Figure 6-3
The algorithm, in comments

Now you can press Tab to indent the region.

Sometimes, if an editor does the commenting for you, it will use a style of commenting we haven’t covered yet: bracketing the comments in /* and */. That works too.

May as well code the easy parts first: the declaration of radius and the loop:

int main (int argc, char** argv)

{

double radius = 200.0; // start radius at 200

{

// draw a circle at center of screen, with this radius

// divide radius by √2

}

while (radius > 1.0); // quit when circle's too small to see

return 0;

}

Now put the middle steps in code, keeping the algorithm as comments:

int main (int argc, char** argv)

{

double radius = 200.0; // start radius at 200

{

// draw a circle at center of screen, with this radius

SSDL_RenderDrawCircle (CENTER_X, CENTER_Y, int (radius));

radius /= sqrt (2); // divide radius by √2

}

while (radius > 1.0); // quit when circle's too small to see

return 0;

}

Looks like we need the center point:

int main (int argc, char** argv)

{

const int CENTER_X = SSDL_GetWindowWidth ()/2;

const int CENTER_Y = SSDL_GetWindowHeight()/2;

double radius = 200.0; // start radius at 200

{

// draw a circle at center of screen, with this radius

SSDL_RenderDrawCircle (CENTER_X, CENTER_Y, int (radius));

radius /= sqrt (2); // divide radius by √2

}

while (radius > 1.0); // quit when circle's too small to see

return 0;

}

Put some friendliness at the program’s start and our usual wrap-up, and we have our program complete and already commented (Example 6-1).

// Program to draw concentric circles

// Each circle is half the area of the one outside it

// -- from _C++20 for Lazy Programmers_

#include <cmath> // for sqrt

#include "SSDL.h"

int main (int argc, char** argv)

{

SSDL_SetWindowTitle ("Hit any key to exit.");

const int CENTER_X = SSDL_GetWindowWidth ();

const int CENTER_Y = SSDL_GetWindowHeight();

double radius = 200.0; // start radius at 200

{

// draw a circle at center of screen, with this radius

SSDL_RenderDrawCircle (CENTER_X/2, CENTER_Y/2, int (radius));

radius /= sqrt (2); // divide radius by √2

}

while (radius > 1.0); // quit when circle's too small to see

SSDL_WaitKey();

return 0;

}

Example 6-1

A program to draw concentric circles, each half the area of the one outside it. Output is in Figure 6-3

Note how the program is broken by blank lines into the major steps from the algorithm. This isn’t a requirement, but it’s not a bad idea.

Online Extra

“When you just can’t figure a way to get started”: find it in the YouTube channel “Programming the Lazy Way,” or at www.youtube.com/watch?v=UJK4a623D20.

Exercises

1.
Write an algorithm to find the average of three numbers.
2.
Write the corresponding program for Exercise 1.
3.
Write an algorithm, then a program, to draw a filled circle, by drawing many circles with radii ranging from 0 to some radius R. It doesn’t have to look completely filled.
4.
Write the algorithm for a program to draw the Australian flag, the New Zealand flag, the Ethiopian flag, a Scandinavian flag, or some other flag using shapes you can draw with SSDL. Concentrate on what makes a coherent subtask or a repeated subtask. We’ll be seeing more flag problems in subsequent chapters.