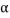Case study–Python for chi-square independence test
A team member examines an annual report that shows the number of resin batches produced by each of four reactors during each of three shifts. She performs a chi-square independence test to determine whether the reactor and shift are associated.
Since the p-value is less than 0.05, she rejects the null hypothesis and concludes that there is an association between reactor and shift variables.
A Chi-square independence test is used to test whether the row and the column variables are associated in a contingency table. The table has R rows and C columns in that the observations with two variables (V1 and V2) are classified into one of R mutually exclusive categories for V1 and one of C mutually exclusive categories for V2.
The following is the mathematical formula for chi-square independence test:
[21]
H0
: The two-way table is independent
Ha
: The two-way table is not independent
Where:
T = the test statistic
r = the number of rows in the contingency table
c = the number of columns in the contingency table
O
ij
=
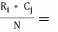
the observed frequency of the ith row and jth column
Eij
= the expected frequency of the ith row and jth column.
Critical region: T >
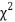 1-α / (r-1) * (c-1)
1-α / (r-1) * (c-1)
Where:
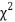 1-α / (r-1) * (c-1)
1-α / (r-1) * (c-1)
= the critical value of the chi-square distribution with (r – 1) * (c-1) degrees of freedom and the significant level of
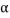
Chi-square independence test using Python follows the following steps.
Step 1. Import libraries.
In [1]:
from scipy import stats
import pandas as pd
Step 2. Load and examine the dataset.
In [2]:
df = pd.read_excel('case chi square table.xlsx')
In [3]:
print(df)
Reactor 1st shift 2nd shift 3rd shift
0 1 119 117 119
1 2 192 117 78
2 3 88 98 83
3 4 117 114 11
4
The dataset has four columns. The reactor labels are in the first column. The numbers of batches produced by each of the three shifts are in the rest of the three columns.
Step 3. Set the Reactor column as the index column.
In [4]:
df = df.set_index(['Reactor'])
print(df)
1st shift 2nd shift 3rd shift
Reactor
1 119 117 119
2 192 117 78
3 88 98 83
4 117 114 114
Step 4. Perform chi-square independence test.
In [5]:
stats.chi2_contingency(df)
Out[5]:
(36.10950415733108,
2.624773867337985e-06,
6,
array([[135.08849558, 116.76253687, 103.14896755],
[147.26548673, 127.28761062, 112.44690265],
[102.36283186, 88.47640118, 78.16076696],
[131.28318584, 113.47345133, 100.24336283]]))
The stats.chi2_contingency( ) function performs the chi-square test of independence of variables in a contingency table. Its return has three components: the chi-square test statistic, the p-value of the test, the degree of freedom, and a contingency table in a numpy array format that shows the expected frequencies, based on the marginal sums of the table. The p-value is 2.62e-6.


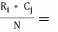 the observed frequency of the ith row and jth column
the observed frequency of the ith row and jth column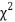 1-α / (r-1) * (c-1)
1-α / (r-1) * (c-1)
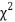 1-α / (r-1) * (c-1)
= the critical value of the chi-square distribution with (r – 1) * (c-1) degrees of freedom and the significant level of
1-α / (r-1) * (c-1)
= the critical value of the chi-square distribution with (r – 1) * (c-1) degrees of freedom and the significant level of