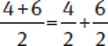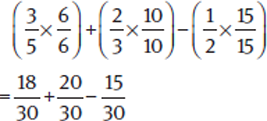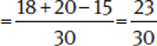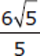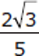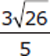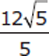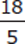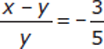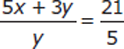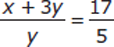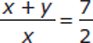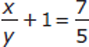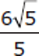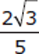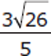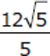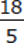CHAPTER 13

Arithmetic on the GMAT

If x is a number such that −2 ≤ x ≤ 2, which of the following has the largest possible absolute value?

• 3x − 1

• x² − x

• 3 − x

• x − 3

• x² + 1

Above is a typical Problem Solving arithmetic question. In this chapter, we’ll look at how to apply the Kaplan Method to this question, discuss the arithmetic rules being tested, and go over the basic principles and strategies that you want to keep in mind on every Quantitative question involving arithmetic. But before you move on, take a minute to think about what you see in this question and answer some questions about how you think it works:

• What mathematical concepts are being tested in this question?

   

• What do you notice about the answer choices?

   

• How do the math concepts in the question relate to the answer choices?

   

• What GMAT Core Competencies are most essential to success on this question?

PREVIEWING ARITHMETIC ON THE GMAT

Most of the Quantitative questions you will see on the GMAT involve arithmetic to some extent. The GMAT frequently increases the difficulty level of questions by combining various topics, such as absolute value, inequalities, exponents, and fractions, and often incorporating these topics into questions that involve algebra, geometry, or proportions. You will be in a much stronger position on Test Day if you have these definitions and operations down cold, freeing up your brain to focus on the more complex critical thinking tasks these difficult and often abstract questions require. This chapter will guide you through the basics and give you practice applying arithmetic concepts to GMAT questions ranging from the simple to the most advanced.

What Mathematical Concepts Are Being Tested in This Question?

As is often the case with GMAT Quantitative questions, a couple of different yet related concepts are involved within this single question. Here, the question gives a range of possible values of x. So you’re looking at inequalities, dealing with both positive and negative numbers. The question itself asks about absolute value, a different topic, but very much related to inequalities, as you’ll see later in this chapter.

What Do You Notice about the Answer Choices?

Each answer choice contains one variable, x, which makes the question seem a little more straightforward. However, note that a few of the answer choices contain x², which introduces more complexity, in that you must understand the behavior of exponential expressions.

How Do the Math Concepts in the Question Relate to the Answer Choices?

Absolute value is the measure of a number’s distance from zero on the number line. (Because 5 and −5 are the same distance from zero—5 units—both numbers have the same absolute value: 5.) When squaring a term, the result will always be non-negative. So even though the possible values of x are both positive and negative, certain answer choices will test your ability to recognize this property of terms raised to even exponents.

What Core Competencies Are Most Essential to Success on This Question?

Here, the testmaker rewards those who understand how paying Attention to the Right Detail is important to answering the question correctly. Despite the basic nature of some of the math topics, the GMAT ultimately rewards test takers who not only know the rules but can apply them to answer questions most efficiently.

Here are the main topics we’ll cover in this chapter:

• Arithmetic Basics

• Fractions and Decimals

• Exponents

• Radicals

• Absolute Value

• Inequalities

Handling GMAT Arithmetic

Now let’s apply the Kaplan Method to the arithmetic question you saw earlier:

If x is a number such that −2 ≤ x ≤ 2, which of the following has the largest possible absolute value?

• 3x − 1

• x² − x

• 3 − x

• x − 3

• x² + 1

Step 1: Analyze the Question

This is an abstract question for which the answer choices contain variables, so Picking Numbers will be a very efficient strategy to use. Since you are asked to find the answer choice that yields the largest absolute value, you should pick numbers at the ends of the range of possible values for x. You will need to check all of the answer choices, so even though this is a “which of the following” question, there is no benefit to starting with (E).

Step 2: State the Task

Evaluate each answer choice, using both x = 2 or x = −2 (the values for x with the greatest possible absolute value), in order to determine which choice will produce the largest absolute value.

Step 3: Approach Strategically

You’ll need to plug in those values of x, but first notice choices (C) and (D). 3 − x and x − 3 are negatives of each other, which means they have the same absolute value. Since the question asks for the choice that has the largest possible absolute value, you can eliminate both of these choices. Notice also that with choice (E), the absolute value will be the same if using 2 or −2, since squaring the x-term will give the same value.

Since the question tests absolute value, plug in −2 first for x in each of the remaining answer choices. Choice (A) gives 3(−2) − 1, which equals −7. The absolute value of −7 is equal to 7. Choice (B) gives (−2)² − (−2) = 4 − (−2) = 6, which has an absolute value of 6. Choice (E) gives (−2)² + 1 = 4 + 1 = 5, which has an absolute value of 5. You already know that choice (E) will yield the same absolute value when x = 2, so eliminate choice (E); you already found that choices (A) and (B) give a larger possible absolute value.

Try x = 2 with the remaining two answer choices. In choice (A), 3(2) − 1 = 6 − 1 = 5, and the absolute value of 5 is equal to 5. For choice (B), (2)² − 2 = 4 − 2 = 2, and the absolute value of 2 is equal to 2. The largest absolute value you found was for choice (A), when x = −2. Therefore, (A) is correct.

Step 4: Confirm Your Answer

Confirm that your calculations are correct and that your answer makes sense.

ARITHMETIC BASICS

Order of Operations

If an expression has parentheses within parentheses, work from the innermost out. This mnemonic will help you remember the order of operations: Please Excuse My Dear Aunt Sally (PEMDAS).

Example:  30 − 5 × 4 + (7 − 3)² ÷ 8

First, perform any operations within parentheses.	30 − 5 × 4 + 42 ÷ 8
Next, raise to any powers indicated by exponents.	30 − 5 × 4 + 16 ÷ 8
Then do all multiplication and division in order from left to right.	30 − 20 + 2
Last, do all addition and subtraction in order from left to right.	10 + 2
Answer:	12

Laws of Operations

These laws will not be tested directly on the GMAT (you won’t need to define what each law is). Focus rather on understanding how to manipulate numbers using the various laws listed below.

Commutative Law

It doesn’t matter in what order the operation is performed. Addition and multiplication are both commutative, while division and subtraction are not commutative.

Example:	5 + 8 = 8 + 5
	2 × 6 = 6 × 2
	3 − 2 ≠ 2 − 3
	6 ÷ 2 ≠ 2 ÷ 6

Associative Law

The terms can be regrouped without changing the result. Addition and multiplication are also associative, while division and subtraction are not.

Example:	(a + b) + c = a + (b + c)	(a × b) × c = a × (b × c)
	(3 + 5) + 8 = 3 + (5 + 8)	(4 × 5) × 6 = 4 × (5 × 6)
	8 + 8 = 3 + 13	20 × 6 = 4 × 30
	16 = 16	120 = 120

Distributive Law

The distributive law allows you to “distribute” a factor among the terms being added or subtracted. In general, a(b + c) = ab + ac.

Example:	4(3 + 7) = 4 × 3 + 4 × 7
	4 × 10 = 12 + 28
	40 = 40

Division can be distributed in a similar way.

Example:
	5 = 5

However, when the sum or difference is in the denominator, no distribution is possible.

Example: 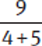  is not equal to .

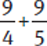Factoring

The technique called factoring uses the distributive law in its reverse form. You can factor to simplify some calculations.

Example:	11 + 22 + 33 + 44
	(11 × 1) + (11 × 2) + (11 × 3) + (11 × 4)
	11 × (1 + 2 + 3 + 4)
	11 × 10
	110

FRACTIONS AND DECIMALS

Fractions

4 ← numerator (also known as the dividend)

— ← fraction bar (means “divided by”)

5 ← denominator (also known as the divisor)

Equivalent Fractions

When you multiply the numerator and denominator by the same number (any number other than zero), the fraction is unchanged. You simply get an equivalent fraction.

Example: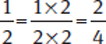  

Similarly, dividing the top and bottom by the same nonzero number leaves the fraction unchanged.

Example: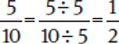    

The GMAT often uses this technique to change the form of fractions that have radicals in the denominator.

Example: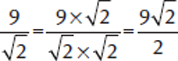  

Canceling and Reducing Fractions

Generally speaking, when you work with fractions on the GMAT, you’ll need to put them in the lowest terms. That means that the numerator and the denominator are not divisible by any common integer greater than 1.

Example:  The fraction is in lowest terms, but the fraction is not, since 3 and 6 are both divisible by 3.

The method you use to take a fraction and put it in lowest terms is called reducing. That simply means to factor and divide out any common multiples from both the numerator and denominator. This process is also commonly called canceling. Canceling is particularly useful to avoid time-consuming calculation.

Example:  Reduce 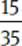to lowest terms.

First, determine the largest common factor of the numerator and denominator. Then, divide the top and bottom by that number to reduce.

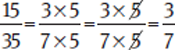
Adding and Subtracting Fractions

We can’t add or subtract two fractions directly unless they have the same, or a “common,” denominator.

A common denominator is just a common multiple of the denominators of the fractions. The least common denominator (LCD) is the least common multiple (LCM): the smallest positive number that is a multiple of all the terms.

Example: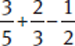  

Denominators are 5, 3, 2.

Least common denominator (LCD) = 30.

For each fraction, divide the LCD by the denominator.

30 ÷ 5 = 6

30 ÷ 3 = 10

30 ÷ 2 = 15

Then, multiply the numerator and denominator by that result.
Combine the numerators by adding or subtracting and keep the LCD as the denominator.

Multiplying Fractions

To multiply fractions, simply multiply the numerators together and the denominators together. Often this process can be sped up by canceling common factors before you multiply.

Example: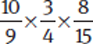  

First, reduce (cancel) diagonally and vertically.

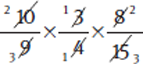
In this case, divide both 10 in the numerator and 15 in the denominator by their common factor 5. Likewise, 3 in the numerator and 9 in the denominator can be reduced by factoring out a 3. Finally, 8 in the numerator and 4 in the denominator can be divided by the common factor 4.

Then multiply the numerators together and the denominators together.

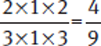
Dividing Fractions

To divide one fraction by another, you actually multiply the first fraction by the reciprocal of the divisor (the second fraction).

To get the reciprocal of a fraction, invert it. Simply switch around the numerator and the denominator. For example, the reciprocal of the fraction is .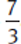

Example: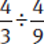  

Invert the divisor, then multiply as usual.

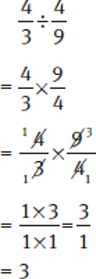
Complex Fractions

A complex fraction is a fraction that contains one or more fractions in its numerator or denominator. There are two methods for simplifying complex fractions.

Method I: Use the distributive law. Find the least common multiple of all the denominators and multiply all the terms in the top and bottom of the complex fraction by the LCM. This will eliminate all the denominators, greatly simplifying the calculation.

Example:

Method II: Treat the numerator and denominator separately. Combine the terms in each to get a single fraction on top and a single fraction on bottom. You are left with the division of two fractions, which you perform by multiplying the top fraction by the reciprocal of the bottom one. This method is preferable when it is difficult to get an LCM for all of the denominators.

Example: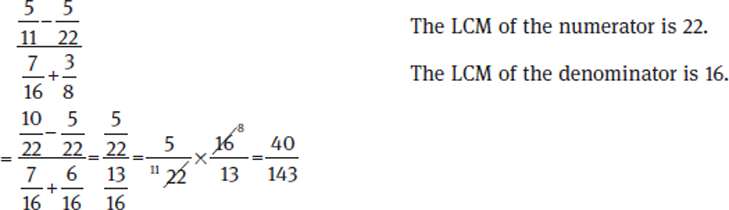

Comparing Positive Fractions

If the numerators are the same, the fraction with the smaller denominator will have the larger value, since the numerator is divided into a smaller number of parts.

Example: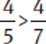  

If the denominators are the same, the fraction with the larger numerator will have the larger value.

Example: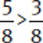  

If neither the numerators nor the denominators are the same, express all of the fractions in terms of some common denominator. The fraction with the largest numerator will be the largest.

One version of this method is to multiply the numerator of the left fraction by the denominator of the right fraction and vice versa (similar to cross multiplying). Then compare the products obtained this way. If the left product is greater, then the left fraction was greater to start with.

Example:   Compare and .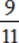

Compare 5 × 11 and 9 × 7.

Because 55 < 63, .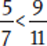

Example:   Compare 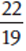and .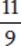

As before, the comparison can be made by cross multiplying.

Compare 22 × 9 and 11 × 19.

Because 198 < 209, .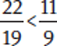

You can also convert the fractions to percents or decimals for easy comparison. This technique is especially useful when finding a common denominator seems time-consuming.

Example:   Compare 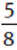, , and .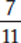

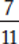= 0.625, = 0.66666 … , and = 0.636363 …

Because 0.625 < 0.636363 … < 0.66666 … , .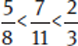

Converting fractions to decimals or percents frequently comes up on the GMAT. Often the problem gives you fractions in the question but percents in the answer choices. It’s a good idea to memorize the common fraction-to-decimal equivalencies for Test Day.

Another way to compare fractions is to find a “benchmark value” against which the fractions can be compared, particularly when dealing with large numbers.

Example:    Compare 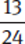and .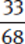

Both are very close to .

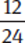= and = .

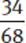Because 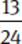> and <, >.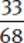

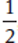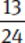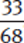Mixed Numbers

Fractions whose numerators are greater than their denominators may be converted into mixed numbers and vice versa. Mixed numbers consist of an integer and a fraction. For example, 3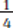, 12, and 5 are all mixed numbers.

Example:  Convert 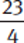to a mixed number.

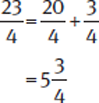
Example:  Convert 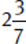to a fraction.

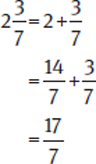
Decimals

Decimals can be converted to common fractions with a power of 10 in the denominator.

Example: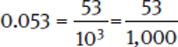  

Numbers are made up of digits in specific places. The GMAT occasionally asks questions using the terms digit and place, so you should be familiar with the naming convention:

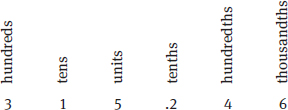
When a GMAT question specifies that a variable is a digit, the only possible values are the integers between 0 and 9, inclusive.

Comparing Decimals

To compare decimals, add zeros after the last digit to the right of the decimal point until all the decimals have the same number of digits. Doing this will make all the denominators of the fractions the same. Therefore, comparing the numerators will determine the order of values.

Example:  Arrange in order from smallest to largest: 0.7, 0.77, 0.07, 0.707, and 0.077.

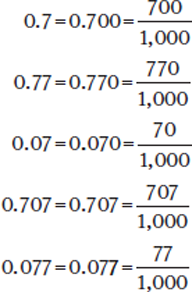
Because 70 < 77 < 700 < 707 < 770, 0.07 < 0.077 < 0.7 < 0.707 < 0.77.

Adding and Subtracting Decimals

When adding or subtracting decimals, make sure that the decimal points are lined up, one under the other. This will ensure that the corresponding places are added: that is, tenths are added to tenths, hundredths to hundredths, etc.

Example: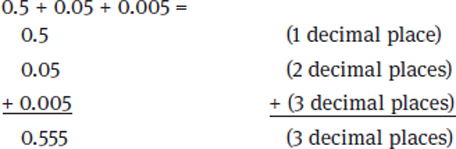

Multiplying and Dividing Decimals

To multiply two decimals, initially multiply them as you would integers and ignore the decimal places. The number of decimal places in the product will be the sum of the number of decimal places in the factors that are multiplied together.

Example: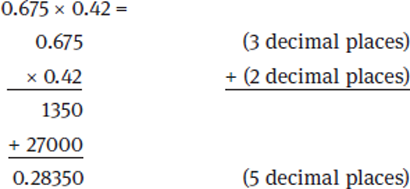

Division—Method I: When dividing a decimal by another decimal, multiply each by a power of 10 such that the divisor becomes an integer; that is, move the decimal point of each the same number of places. (This doesn’t change the value of the quotient.) Then carry out the division as you would with integers, placing the decimal point in the quotient directly above the decimal point in the dividend.

Example:

Division—Method II: Turn the division problem into a fraction. It is best when the numbers have common factors. Move the decimal point in the numerator and the denominator an equivalent number of places to make both numbers integers. Then, cancel common factors.

Example: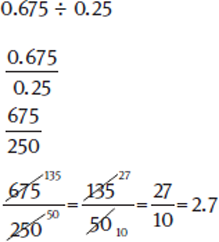

In-Format Question: Fractions and Decimals on the GMAT

Now let’s use the Kaplan Method on a Problem Solving question dealing with fractions:

• 

• 

• 

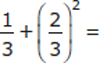
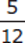
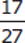
• 1

• 

Step 1: Analyze the Question

You’re given an expression with two fractions, one of which is raised to an exponent. Attention to the Right Detail is important here; in this case, note the use of the parentheses around only one of the fractions.

Step 2: State the Task

Follow the order of operations (PEMDAS); start with the parentheses, then add the fractions by finding a common denominator.

Step 3: Approach Strategically

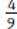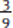First, square both the numerator and denominator of , giving a value of . Then find a common denominator for the two fractions and . Multiply the numerator and denominator of by 3, which yields . Now that the denominators are the same, you can add the two fractions 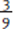+ 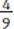, which gives you the answer, , choice (C).

Step 4: Confirm Your Answer

Take a moment to verify your math, particularly making sure you followed the order of operations and accurately converted fractions into forms that have a common denominator. Note that (D) would be a tempting wrong answer if you had first added the two fractions and then squared the result.

TAKEAWAYS: FRACTIONS AND DECIMALS

 

• When adding or subtracting fractions, you must have a common denominator.

• 

• 

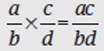
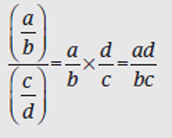
• Knowing common fraction-to-decimal equivalencies will help save you time on Test Day.

Practice Set: Fractions and Decimals on the GMAT

Answers and explanations at end of chapter

1. If z is equal to one of the numbers , , or , what is the value of z?

   • (1)    < z <

   • (2)    < z <

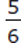
2. The equation − = 0 is equivalent to each of the following EXCEPT

   • = −

   • =

   • =

   • =

   • =

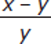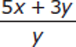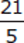
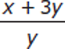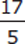
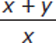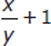3. If xy ≠ 0, is the reciprocal of 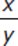greater than ?

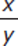   • (1)   x > y

   • (2)   xy > 0

EXPONENTS

Rules of Operations with Exponents

In the term 3x², 3 is the coefficient, x is the base, and 2 is the exponent. The exponent refers to the number of times the base is multiplied by itself. For instance, in 4³, you multiply 4 by itself 3 times: 4³ = 4 × 4 × 4 = 64.

Accurately distinguishing among these elements is important. For instance, in the expression 3x², only the x is being squared (x is the base), not the 3 (3 is the coefficient). In other words, 3x² = 3(x²). If you wanted to square the 3 as well, you would need to rewrite the term as (3x)² to make 3 part of the base. Remember that in the order of operations, you raise to a power before you multiply, so in 3x², you square x and then multiply by 3.

A number multiplied by itself twice is called the square of that number (e.g., 5² is 5 squared).

A number multiplied by itself three times is called the cube of that number (e.g., 4³ is 4 cubed).

To multiply two terms with the same base, keep the base and add the exponents.

Example:  2² × 2³ = 2²⁺³

                             = 2⁵

To divide two terms with the same base, keep the base and subtract the exponent of the denominator from the exponent of the numerator.

Example: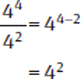  

To raise a power to another power, multiply the exponents.

Example:  (3²)⁴ = 3^2×4

            = 3⁸

To multiply two terms with the same exponent but different bases, multiply the bases together and keep the exponent.

Example:  (2³)(3³) = (2 ^{× 3)3}

                = 6³

Any number raised to the first power equals itself: a¹ = a.

Any number except zero that is raised to the zero power is equal to 1: a⁰ = 1. The exception to this rule is when the base is also equal to zero (0⁰ is undefined).

A negative exponent indicates a reciprocal. To arrive at an equivalent expression, take the reciprocal of the base and change the sign of the exponent.

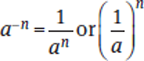
Example: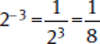    

When raising a fraction to an exponent, you can solve in one of two ways: either by raising the numerator and the denominator to the exponent separately, or by multiplying the whole fraction by itself the number of times indicated by the exponent. Either approach yields the same result.

Example: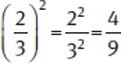  

                    

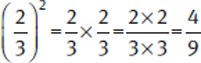
Note that the squared value here, 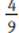, is less than the base, . Raising a positive fraction less than 1 to a positive exponent greater than 1 results in a smaller value. The higher the exponent, the smaller the result.

Bases of 10

The exponent of a base of 10 tells you how many zeros the number would contain if written out.

Example:  10⁶ = 1,000,000 (6 zeros), since 10 multiplied by itself six times is equal to 1,000,000.

When multiplying a number by a power of 10, move the decimal point to the right the same number of places as in the exponent; that is, the number of zeros in that power of 10.

When dividing by a power of 10, move the decimal point the corresponding number of places to the left. (Note that dividing by 10⁴ is the same as multiplying by 10⁻⁴.)

In-Format Question: Exponents on the GMAT

Now let’s use the Kaplan Method on a Data Sufficiency question dealing with exponents:

• Does a = b?

• (1)    a² − b² = 0

• (2)    1 − 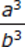=0

Step 1: Analyze the Question Stem

This is a Yes/No question. You need to determine whether there is enough information to answer the question “Does a = b?” There is no information provided in the question stem, so look at the statements.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) says that a² − b² = 0, which is the same as saying a² = b². Now if a² = b², then either a = b or a = −b. You can test a few cases by Picking Numbers. If a = 5 and b = 5, then a² = b², so Statement (1) is true and a = b. The answer to the question is “yes.”

If a = 5 and b = −5, then a² = b² because 5² = (−5)² = 25, so Statement (1) is true and a is not equal to b. The answer to the question is “no.” Because more than one answer to the question is possible, Statement (1) is insufficient. You can eliminate (A) and (D).

Statement (2) tells you that 1 − 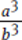= 0, which can be simplified as 1 − 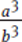or a³ = b³. In the equation a³ = b³, both a and b are raised to the same odd exponent. Remembering the rules governing exponents, you know that when raised to an odd power, positive numbers yield positive results and negative numbers yield negative results. So, if a³ = b³ you can now conclude that a = b. The answer to the question is “always yes,” and Statement (2) is sufficient. The correct answer is (B).

If you weren’t sure about the rules of exponents, you could use Picking Numbers to evaluate Statement (2). In order for a³ to equal b³, a and b must have the same value. For instance, if a = −5 and b = −5, then a³ = b³ because (−5)³ = (−5)³ = −125. You cannot pick numbers such as a = 5 and b = −5, since 5³ = 125 ≠ (−5)³ = −125. Since it’s impossible to pick different numbers for a and b, the answer to the question is “always yes,” and you can choose (B).

Note how the Core Competency of Attention to the Right Detail plays a big role in answering the question correctly. It’s easy to be misled into thinking that if a² = b², then a must be equal to b. Pay attention to whether exponents are even or odd when confronted with a similar problem.

TAKEAWAYS: EXPONENTS

 

• Exponents count the number of times something is multiplied by itself.

• a^b × a^c = a^b+c

• 

• 

• 

• 

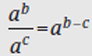
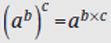
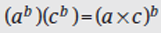
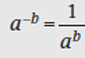
• Raising a positive fraction less than 1 to a positive exponent greater than 1 results in a smaller value. The higher the exponent, the smaller the result.

• When a negative number is raised to an even exponent, the result is positive. When a negative number is raised to an odd exponent, the result is negative.

• When multiplying a number by a power of 10, the exponent just represents the number of places to move the decimal.

Practice Set: Exponents on the GMAT

Answers and explanations at end of chapter

4. If x is an integer and 2.134 × 10^x is less than 210,000, what is the greatest possible value for x?

   • 7

   • 6

   • 5

   • 4

   • 3

5. If 4^2x+2 = 16^3x−1, what is the value of x?

   • 0

   • 1

   • 2

   • 3

   • 4

6. If a is a positive integer, then 2^a + 2^a+1 =

   • 3^a+1

   • 2^a+1

   • 2a

   • 2a^a+1

   • 3(2^a)

RADICALS

Fractions as Exponents

A fractional exponent indicates a root. So 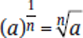(Read “the nth root of a.”) If no specific “n” is present, the radical sign means a square root. If the numerator in the fractional exponent is a different integer, raise the resulting term to that exponent.

Example: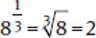    

Example: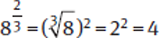    

Rules of Operations with Radical Symbols

By convention, the symbol 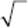(called “radical”) means the positive square root only. Even though there are two different numbers whose square is 9 (both 3 and −3), when you see 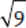on the GMAT, it refers to the positive number 3 only.

Example: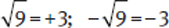  

When it comes to the four basic arithmetic operations, you treat radicals in much the same way you would treat variables.

Addition and Subtraction

Only like radicals can be added to or subtracted from one another.

Example: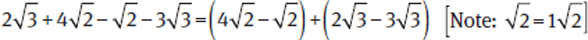  

                                       

                                       

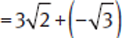
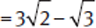
Multiplication and Division

To multiply or divide one radical by another, multiply or divide the numbers outside the radical signs, then the numbers inside the radical signs.

Example: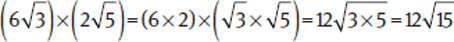  

Example: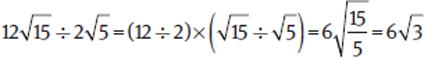  

Example: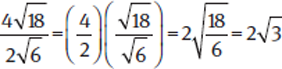  

If the number inside the radical is a multiple of a perfect square, the expression can be simplified by factoring out the perfect square.

Example: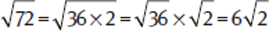  

Warning:  You cannot “split up” addition underneath a radical sign, although the GMAT will try to trick you into thinking you can.

Example:

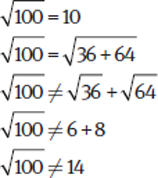
Exponents and Powers of 10 with Radicals

If an exponent is under the square root sign, just divide the exponent by 2. If an exponent is under a cube root sign, divide it by 3.

Example: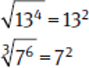

If a decimal is under a square root sign, take the square root of the number and divide the number of decimal places by 2. Likewise, if a decimal is under a cube root sign, take the cube root of the number and divide the number of decimal places by 3.

Example: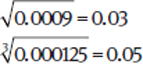

In-Format Question: Radicals on the GMAT

Now let’s use the Kaplan Method on a Problem Solving question dealing with radicals:

• 

  • 

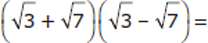
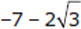
  • −4

  • 3

  • 

  • 

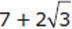
Step 1: Analyze the Question

You have to multiply two expressions with square roots in the terms. Note that the numbers under the radical signs are the same; this may be a signal to look at the question more strategically.

Step 2: State the Task

To begin, recall that 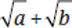does not equal 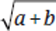. Also, 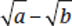does not equal 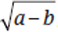. Thus, in this question, you cannot combine the radicals inside the parentheses; instead, you need to multiply the expressions 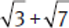and 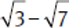using FOIL.

Step 3: Approach Strategically

If you’ve memorized the classic quadratic equations, you might recognize the expression in the stem as the factors of the difference of two squares. Recognizing this pattern will save you time, since you can avoid going through the entire process of applying FOIL.

Remember that (a ^{+ b)(a − b) = a2 − b2.}

Substitute 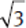for a, and 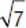for b. Then you have 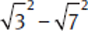, or 3 − 7, which equals −4.

If you hadn’t noticed the shortcut, you could have applied FOIL:

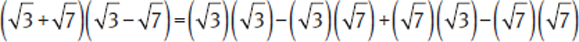
Now, 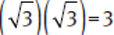and 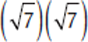= 7, so you are left with 3 − 0 − 7 = −4.

Either way, (B) is correct.

Step 4: Confirm Your Answer

Quickly double-check the last calculation step, and you’re done.

TAKEAWAYS: RADICALS

 

• Radicals follow the same rules as exponents.

• 

• 

• 

• 

• 

• 

• 

• 

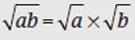
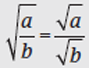
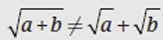
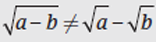
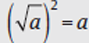
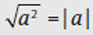
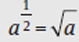
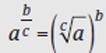
Practice Set: Radicals on the GMAT

Answers and explanations at end of chapter

7. 

   • 

   • 

   • 

   • 

   • 

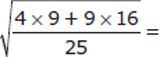
8. What positive number, when squared, is equal to the cube of the positive square root of 16?

   • 64

   • 32

   • 8

   • 4

   • 2

9. If r > 0, is 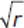an integer?

   • (1)   r² is an integer.

   • (2)   r = m², where m is an integer.

ABSOLUTE VALUE

The absolute value of a number is the number’s distance from zero on the number line. It is denoted by two vertical lines. Since absolute value is a distance, it is always non-negative. For instance, both +3 and −3 are 3 units from zero, so their absolute values are both 3.

Example:  |−3| = 3

    |+3| = 3

The GMAT will increase the difficulty of an absolute value question (and, therefore, the benefit of getting it right) by using variables.

Example:  |z| = 3

You don’t know what z equals. Since z is 3 units from 0, you can deduce that it either equals +3 or −3.

So you can rewrite this one equation as two:

z = 3 OR z = −3

Another way to conceptualize this is as follows:

|z| = 3

±z = 3

+z = 3 OR −z = 3

z = 3 OR z = −3

These problems are fairly straightforward when only one number is involved. But what about expressions? Treat the absolute value bars as parentheses and figure out the value of what’s inside before you perform the operation. Needless to say, the GMAT will base wrong answers on performing these operations in the wrong order.

INCORRECT:     |−3| + |5| = |−3 + 5| = |2| = 2

CORRECT:      |−3| + |5| = 3 + 5 = 8

Now, let’s look at what happens when you are given expressions with variables.

Example:  |x − 3| = 3

Believe it or not, this isn’t any different from the earlier example:

|z| = 3

z = 3 OR z = −3

Think of it this way:

|<<chunk>>| = 3

<<chunk>> = 3 OR <<chunk>> = −3

Since the <<chunk>> here is x − 3, that gives you the following:

|x − 3| = 3

x − 3 = 3 OR x − 3 = −3

x = 6 OR x = 0

The GMAT sometimes adds another layer of complexity to absolute value questions by including inequalities. The key is to remember that when considering the possible negative value, the inequality sign changes direction:

|x − z| > 3

x − z > 3 OR x − z < −3

Don’t worry if that concept seems a little strange to you right now. We’ll explore this idea further when we discuss inequalities later in this chapter.

In-Format Question: Absolute Value on the GMAT

Now let’s use the Kaplan Method on a Problem Solving question dealing with absolute value:

• How many possible integer values are there for x, if |4x − 3| < 6?

  • One

  • Two

  • Three

  • Four

  • Five

Step 1: Analyze the Question

You’re asked for the number of integers that could satisfy an inequality. The inequality includes an expression with an absolute value.

Step 2: State the Task

You’ll have to evaluate the inequality, find the range of x on the number line, and then count the number of integers that could be acceptable values of x. Remember that the correct answer is not any particular value of x, but the number of possible integer values.

Step 3: Approach Strategically

When you have an absolute value in an expression, you have to consider two possibilities: either 4x − 3 < 6 or −(4x − 3) < 6. Multiply both sides of the second inequality by −1, remembering to reverse the inequality sign: the second inequality can be written as 4x − 3 > −6. Combine these two statements to analyze the expression more quickly: −6 < 4x − 3 < 6. Adding 3 to each of the three members, you have −3 < 4x < 9. Dividing each of the three members by 4 gives you − < x < 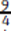;. The possible integer values of x such that − < x < 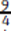are 0, 1, and 2. Answer choice (C) is correct.

Step 4: Confirm Your Answer

Confirm that your calculations are correct. Quickly sketch the range of x on a number line to confirm your count of the number of possible integer values of x.

TAKEAWAYS: ABSOLUTE VALUE

 

• Use these three tools to solve absolute value problems:

  1. Interpret absolute value as the expression’s distance from zero on the number line.

  2. Draw a number line.

  3. Write two equations for every equation with an absolute value; one or the other of these new equations must be true.

• When there is an absolute value sign, there is a high likelihood of a trap answer for those who assume the quantity inside can only be positive.

Practice Set: Absolute Value on the GMAT

Answers and explanations at end of chapter

10. Which of the following could be the value of x, if |4x − 2| = 10?

    • −3

    • −2

    • 1

    • 2

    • 4

11. What is the value of p?

    • (1)   −|p| = −2

    • (2)   p² − 4 = 0

12. If 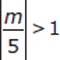, then which of the following must be true?

    • m > 5

    • m < 5

    • m = 5

    • m ≠ 5

    • m < −5

INEQUALITIES

Inequality Symbols

> greater than	Example: x > 4 means x is greater than 4.
< less than	Example: x < 0 means x is less than zero (x is a negative number).
≥ greater than or equal to	Example: x ≥ −2 means x can be −2 or any number greater than −2.
≤ less than or equal to	Example: x ≤ means x can be or any number less than .

A range of values is often expressed on a number line. Two ranges are shown below.

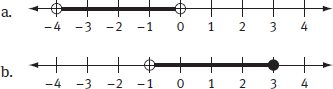
(a) represents the set of all numbers between −4 and 0, excluding the endpoints −4 and 0, or −4 < x < 0.

(b) represents the set of all numbers greater than −1, up to and including 3, or −1 < x ≤ 3.

Sketching a number line is a great way to help yourself to visualize inequalities on Test Day.

Solving Inequalities

To solve inequalities, you use the same methods as used in solving equations with one exception: if the inequality is multiplied or divided by a negative number, the direction of the inequality is reversed.

If the inequality −3x < 2 is multiplied by −1, the resulting inequality is 3x > −2.

Example:  Solve for x and represent the solution set on a number line: 3 − ≥ 2.

Multiply both sides by 4.	12 − x ≥ 8
Subtract 12 from both sides.	−x ≥ −4
Divide both sides by −1 and change the direction of the sign.	x ≤ 4

Note that the solution set to an inequality is not a single value but a range of possible values. Here, the values include 4 and all numbers less than 4.

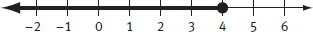
Example:    Describe the possible values for x if |2x − 5| < 3.

With an absolute value, you must split the inequality into two: one with a positive number and one with a negative number. But you must reverse the direction of the inequality sign in the negative case:

|2x − 5| < 3

2x − 5 < 3     AND    2x − 5 > −3

2x < 8     AND        2x > 2

x < 4     AND        x > 1

1 < x < 4

You also need to watch out for this possibility when multiplying or dividing by variables.

Example:  Simplify 3b < 2b².

3b < 2b²

Divide both sides by b:	Before you can do so, you must know whether b is negative.
Write down both possibilities:	If b is neg.	OR	If b is pos.
	3 > 2b	OR	3 < 2b
Divide by 2:	> b	OR	< b

All negative numbers are less than , so b could equal any negative number at all or any positive number greater than .

b < 0   OR   < b

Three-Part Inequalities

If you are given a three-part inequality, you can still perform calculations on it. But instead of saying, “What I do to one side, I must also do to the other,” you say, “What I do to one part, I must do to all parts.”

Example:  Simplify −11 < 2x − 5 < 1.

                                        −11 < 2x − 5 < 1

add 5 to all parts:              −11 + 5 < 2x − 5 + 5 < 1 + 5

combine like terms:           −6 < 2x < 6

divide all parts by 2:          −3 < x < 3

In-Format Question: Inequalities on the GMAT

Now let’s use the Kaplan Method to solve a Problem Solving question dealing with inequalities:

• If x > 4 and 3x − 2y = 0, then which of the following must be true?

  • y < −6

  • y < −4

  • y = 6

  • y < 6

  • y > 6

Step 1: Analyze the Question

You’re given an equation with two variables and an inequality giving you a range of values for one of the variables. Using this information, and scanning the answer choices, you need to determine what will always be true of y for the equation and the inequality to be true.

Step 2: State the Task

Solve the equation for x in terms of y, then substitute the resulting expression for x into the inequality. Finally, evaluate the answer choices and determine which must be true.

Step 3: Approach Strategically

You should start by solving the equation for x as follows:

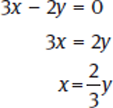
Because you know that x > 4, you can replace x with the value of the equation, so 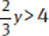. You can plow through with the calculations here, but by applying Critical Thinking, you can actually get the right answer now. Since multiplying y by a proper fraction must be larger than 4, then y itself must be larger than 4 as well. Since there’s no other limitation, find the answer choice that gives you a range of results that are all larger than 4. The only choice that does that is choice (E).

Step 4: Confirm Your Answer

You can confirm your answer using traditional math: multiply both sides of the inequality 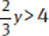by 3. So, 2y > 12. Next, divide both sides of this inequality by 2, which leads to the conclusion that y > 6. Answer choice (E) is correct.

TAKEAWAYS: INEQUALITIES

 

Inequalities should be treated exactly as equations, with two exceptions:

1. When you multiply or divide an inequality by a negative number, you must reverse the direction of the inequality sign.

2. Single-variable equations are usually solved for a specific value, whereas inequalities can only be solved for a range of values.

Practice Set: Inequalities on the GMAT

Answers and explanations at end of chapter

13. Is x ≤ 3?

    • (1)   6x ≤ 24

    • (2)   3x + 1 ≥ 12

14. How many integer values are there for x such that 1 < 3x + 5 < 17?

    • Two

    • Three

    • Four

    • Five

    • Six

15. If b ≠ 0 and a > b, is a > c?

    • (1)   

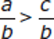
    • (2)   5ab > 6bc

Answer Key

Practice Set: Fractions and Decimals on the GMAT

1. E

2. B

3. E

Practice Set: Exponents on the GMAT

4. D

5. B

6. E

Practice Set: Radicals on the GMAT

7. A

8. C

9. B

Practice Set: Absolute Value on the GMAT

10. B

11. E

12. D

Practice Set: Inequalities on the GMAT

13. B

14. D

15. E

Answers and Explanations

Practice Set: Fractions and Decimals on the GMAT

1.    (E)

If z is equal to one of the numbers , , or , what is the value of z?

• (1)    < z <

• (1)    < z <

Step 1: Analyze the Question Stem

This is a Value question. The question stem restricts the value of z to three possible fractions. For sufficiency, we need to narrow this list down to one and only one fraction. It can be hard to compare fractions that have different denominators, so it helps to know the fraction-to-decimal equivalents. We should convert the three fractions in the question stem before proceeding: = 0.6, 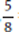= 0.625, and = .

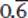Step 2: Evaluate the Statements Using 12TEN

Statement (1) places z somewhere between 0.5 and 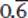. That removes from the list of possibilities but still leaves and 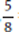in the running, so this statement is insufficient. Eliminate (A) and (D).

Statement (2) places z somewhere between and . The decimal equivalent of may not be a familiar one, but dividing 9 into 5 gives you 0.5 followed by something, so is definitely less than . As = < , this statement does not actually narrow down the given list of fractions at all and is therefore insufficient. Eliminate (B).

Combining the statements does no good because Statement (2) gave us no useful information that wasn’t provided in Statement (1). Eliminate (C).

The statements even when combined are insufficient, so the correct answer is (E).

2.    (B)

The equation − = 0 is equivalent to each of the following EXCEPT

• 

• 

• 

• 

• 

Step 1: Analyze the Question

Our question tells us that four of our answer choices are equivalent to − = 0 and one isn’t. Because this is an EXCEPT question, our correct answer is the answer choice that is not equivalent. With variables in the question stem and variables in the answer choices, this is a classic question for Picking Numbers.

Step 2: State the Task

Some straightforward numbers to use for the initial equation would be x = 2 and y = 5. Let’s plug these into the five answer choices, starting with (E) because this is a “which of the following” question. Remember, we’re looking for the answer choice that doesn’t work.

Step 3: Approach Strategically

(E) 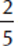+ 1 = . This works. We must keep this choice for now.

(D) 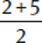= . This also works. We must keep this choice for now.

(C) 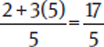. This also works. We must keep this choice for now.

(B) 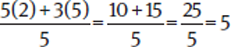. Because 5 ≠ 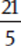, this does not work and must be our answer.

Because we know that choice (B) is not equivalent to the equation − = 0 of the question stem, there is no need to check choice (A).

Step 4: Confirm Your Answer

Confirm that your calculations for answer choice (B) are correct.

3.    (E)

If xy ≠ 0, is the reciprocal of greater than ?

• (1)   x > y

• (2)   xy > 0

Step 1: Analyze the Question Stem

This is a Yes/No question. The question stem only tells us that the product of the two variables is not equal to zero, so we know that neither variable is equal to zero. Next we want to rephrase the question in a simpler format: Is > ?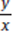

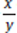Step 2: Evaluate the Statements Using 12TEN

Statement (1) tells us that x > y. Picking positive numbers, if x = 3 and y = 2, we find that is not greater than and the answer to the question is “no.” Picking negative numbers, if x = −1 and y = −2, we find that 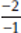is greater than 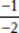and the answer to the question is “yes.” Statement (1) is insufficient. We can eliminate (A) and (D).

Statement (2) tells us the product of x and y is positive, so we know that x and y are either both positive or both negative. Because the numbers we picked for Statement (1) already fall into that category, we can immediately tell that Statement (2) is also insufficient. We can eliminate (B).

As the numbers we picked could be used for either Statement (1) or (2), they can still be used when we combine the information from both statements. Therefore, even when the statements are taken together, it is still not possible to get a definite answer. Choice (E) is correct.

Practice Set: Exponents on the GMAT

4.    (D)

If x is an integer and 2.134 × 10^x is less than 210,000, what is the greatest possible value for x?

• 7

• 6

• 5

• 4

• 3

Step 1: Analyze the Question

We know two things about x: it’s an integer, and 2.134 × 10^x < 210,000.

Step 2: State the Task

Find the greatest possible value for x.

Step 3: Approach Strategically

To multiply a decimal quantity by 10^x, move the decimal point x places to the right. For 2.134, moving the decimal point 5 places to the right results in the number 213,400. That’s just over the limit of 210,000, so the maximum value of x is 4. The correct answer is (D).

Step 4: Confirm Your Answer

A great way to confirm the answer on this type of question is to write the number down on your noteboard before counting the number of decimal places to move.

5.    (B)

If 4^2x+2 = 16^3x−1, what is the value of x?

• 0

• 1

• 2

• 3

• 4

Step 1: Analyze the Question

We have to solve for x in an equation with exponents. The bases of the two terms with exponents are not the same, but we notice that one of the bases, 16, is equal to the other one, 4, squared.

Step 2: State the Task

We have manageable numbers in the answer choices, so we can approach this question algebraically or by Backsolving.

Step 3: Approach Strategically

Let’s use Backsolving first. Although it would be difficult to know after testing an incorrect answer choice whether the right answer should be larger or smaller, Backsolving may still be the most efficient solution, since the answer choices are all small, manageable integers. Remember, you should always start Backsolving with choice (B) or (D). In choice (B), x = 1, which is an easy value to test. Substituting 1 for x will give us 4²⁽¹⁾⁺² = 16³⁽¹⁾⁻¹, 4²⁺² = 16³⁻¹, and 4⁴ = 16². Replacing 16 with 4², we get 4⁴ = (4²)², or 4⁴ = 4⁴, which is true. Choice (B) is correct.

Now let’s solve the question algebraically. We noticed that 16 = 4², so we can replace the 16 with 4² on the right side of the equation, as 4 is the base on the left side of the equation. Then 4^2x+2 = (4²)^3x−1. When a power is raised to an exponent, we take the product of the exponents and keep the same base. Algebraically, (a^b)^c = a^bc. So using this rule on the right side of the equation 4^2x+2 = (4²)^3x−1, we get 4^2x+2 = 4^2(3x−1).

When equal powers have the same base, where that same base is not 1, 0, or −1, the exponents must be equal. So 2x + 2 = 2(3x − 1). Let’s solve this equation for x. We have

2x + 2 = 2(3x − 1)

2x + 2 = 6x − 2

4 = 4x

x = 1

Step 4: Confirm Your Answer

If you chose Backsolving, confirm that your calculations for answer choice (B) are correct.

If you chose to solve algebraically, confirm by quickly substituting 1 for x in the question stem.

6.    (E)

If a is a positive integer, then 2^a + 2^a+1 =

• 3^a+1

• 2^a+1

• 2a

• 2a^a+1

• 3(2^a)

Step 1: Analyze the Question

We have to evaluate an expression with exponents. We notice the bases of the two terms are equal, but we’re adding the terms, not multiplying them. We’ll have to use a strategy or think critically in applying the exponent rules.

Step 2: State the Task

We have variables in the answer choices, so we can approach this question algebraically or by Picking Numbers.

Step 3: Approach Strategically

When using the Picking Numbers strategy, all four incorrect answer choices must be eliminated because sometimes one or more incorrect answer choices will work for the particular value that we choose.

Let’s use a = 1. Then 2^a + 2^a+1 = 2¹ + 2¹⁺¹ = 2¹ +2² = 2 + 4 = 6.

Now let’s substitute 1 for a into each answer choice. Any answer choice that does not equal 6 when a = 1 can be eliminated.

(A) is 3^a+1 = 3² = 9. This is not 6, so we can eliminate (A).

(B) is 2^a+1 = 2¹⁺¹ = 2² = 4. This is not 6, so we can eliminate (B).

(C) is 2a = 2(1) = 2. This is not 6, so we can eliminate (C).

(D) is 2a^a+1 = 2(1¹⁺¹) = 2(1²) = 2. This is not 6, so we can eliminate (D).

Now that all four incorrect answer choices have been eliminated, we know that (E) must be correct.

We can also solve this question algebraically. To evaluate 2^a+1, we recall that when multiplying two numbers with the same base, we add the exponents. So 2^a+1 = 2^a(2¹), and our original expression 2^a + 2^a+1 = 2^a + 2^a(2¹) = 2^a(1 + 2) = 2^a(3) = 3(2^a). Choice (E) is correct.

Step 4: Confirm Your Answer

If you chose to Pick Numbers, you can confirm your answer by checking (E): 3(2^a) = 3(2¹) = 3(2) = 6. Choice (E) does work.

If you chose to solve algebraically, confirm that your calculations are correct.

Practice Set: Radicals on the GMAT

7.    (A)

• 

• 

• 

• 

• 

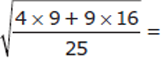
Step 1: Analyze the Question

We are given a radical expression to simplify.

Step 2: State the Task

Our task is to simplify the given radical expression.

Step 3: Approach Strategically

Straightforward math is the best approach here. We need to make sure we remember the rules for performing operations on radicals and when we can and cannot combine them. We should also look for common factors so that we can avoid unnecessary calculations.

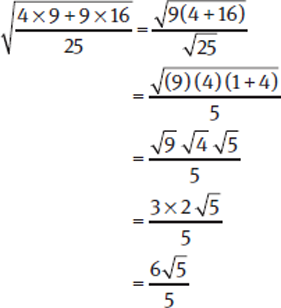
The correct answer is (A).

Step 4: Confirm Your Answer

With arithmetic, remember to follow PEMDAS, the order of operations. On this problem, be sure to do all of the multiplication before any of the addition in the numerator.

8.    (C)

What positive number, when squared, is equal to the cube of the positive square root of 16?

• 64

• 32

• 8

• 4

• 2

Step 1: Analyze the Question

We need to find a number that meets the requirements of the question stem.

Step 2: State the Task

We’ll have to translate the information in the question stem into algebra so we can solve for our answer.

Step 3: Approach Strategically

We’ll call the positive number the question is asking us for n. When this number is squared, we obtain n². We are told that n² is equal to the cube of the positive square root of 16. Let’s start with the number we’re given and work step-by-step. The positive square root of 16 is 4. The cube of the positive square root of 16 is the cube of 4: 4³ is 4 × 4 × 4 = 64. Therefore, n² = 64. Because n > 0, n is the positive square root of 64. So n = 8. Choice (C) is correct.

Step 4: Confirm Your Answer

Reread the question stem and confirm that your translations and calculations are correct.

9.    (B)

If r > 0, is 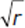an integer?

• (1)   r² is an integer.

• (2)   r = m², where m is an integer.

Step 1: Analyze the Question Stem

This is a Yes/No question. Here we are given that r is positive, and we need to find out whether we have sufficient information to determine whether 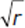is an integer. There is no information in the question stem that we can use to determine whether or not 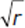is an integer, so let’s look at the statements.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) says that r² is an integer. If r = 4, then r² = 4² = 16 is an integer, so Statement (1) is true. In this case, 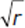= =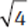 2 is an integer, and the answer to the question is “yes.” If r = 5, then r² = 5² = 25 is an integer, so Statement (1) is true. In this case, 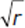= 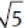is not an integer, and the answer to the question is “no.” Because different answers to the question are possible, this statement is insufficient. We can eliminate (A) and (D).

Now let’s look at Statement (2). If r = m² , where m is an integer, then 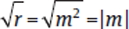. Thus, 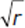must always be an integer, since we are told that m is an integer. Statement (2) is sufficient, so (B) is correct.

Practice Set: Absolute Value on the GMAT

10.   (B)

Which of the following could be the value of x, if |4x − 2| = 10?

• −3

• −2

• 1

• 2

• 4

Step 1: Analyze the Question

We are given the equation |4x − 2| = 10.

Step 2: State the Task

Find the possible value of x.

Step 3: Approach Strategically

If |4x − 2| = 10, the quantity inside the absolute value signs must equal either 10 or −10, so we should solve for x by breaking the equation into 4x − 2 = 10 and 4x − 2 = −10.

If 4x − 2 = 10, then 4x = 12 and x = 3.

If 4x − 2 = −10, then 4x = −8 and x = −2.

3 isn’t one of the answer choices, but −2 is correct choice (B).

Step 4: Confirm Your Answer

To confirm our answer, we can Backsolve, plugging −2 in for x in the original equation: |4(−2) −2| = |−8 − 2| = |−10| = 10. Choice (B) is confirmed as correct.

11.   (E)

What is the value of p?

• (1)   −|p| = −2

• (2)   p² − 4 = 0

Step 1: Analyze the Question Stem

This is a Value question. We need to be able to determine a single value for p. There is no information in the question stem that we can use to determine p, so let’s look at the statements.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) tells us that p can equal either −2 or 2, so it is not sufficient to determine a single value for p. We can eliminate (A) and (D).

Statement (2) tells us that p² = 4, so p equals either −2 or 2; this too is insufficient. We can eliminate (B).

When we combine the statements, we still have the same two possible values, so even together, the statements are insufficient. Answer choice (E) is correct.

12.   (D)

If 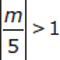, then which of the following must be true?

• m > 5

• m < 5

• m = 5

• m ≠ 5

• m < −5

Step 1: Analyze the Question

We have to evaluate an inequality and then determine which of the answer choices is always true. The inequality contains an expression with absolute value signs.

Step 2: State the Task

We’ll have to evaluate the inequality, find the range of m on the number line, and then evaluate the answer choices.

Step 3: Approach Strategically

When we have an absolute value in an expression, we have to consider both possibilities: Either 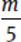> 1 OR 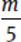< −1.

So m > 5 OR m < −5.

Remember that when we multiplied by −5 in the second possibility, we changed the direction of the inequality sign.

Now we’re ready to evaluate the choices. Remember, we’re looking for the choice that is always true. Each of choices (A), (B), and (E) could be true but does not have to be. (C) is never true given the question stem. (D) is the only choice that must be true.

Step 4: Confirm Your Answer

Confirm that your calculations are correct. A quick sketch of the range of m on a number line shows our answer is correct.

Practice Set: Inequalities on the GMAT

13.   (B)

Is x ≤ 3?

• (1) 6x ≤ 24

• (2) 3x + 1 ≥ 12

Step 1: Analyze the Question Stem

In this Yes/No question, sufficiency means demonstrating that x is either definitely less than or equal to 3, or that x is definitely greater than 3.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) states that 6x ≤ 24, which simplifies to x ≤ 4. That allows x to be less than 3 but also allows x to be 3 or greater, so this statement is insufficient. Eliminate (A) and (D).

Statement (2) states that 3x + 1 ≥ 12, which simplifies to 3x ≥ 11. While we still do not know the value of x, we don’t need to, as x is definitely greater than 3. This statement results in a definite “no,” so it is sufficient. Eliminate (C) and (E).

Statement (2) alone is sufficient, so the correct answer is (B).

14.   (D)

How many integer values are there for x such that 1 < 3x + 5 < 17?

• Two

• Three

• Four

• Five

• Six

Step 1: Analyze the Question

We’re asked for the number of integers that could satisfy an inequality.

Step 2: State the Task

We’ll have to evaluate the inequality, find the range of x on the number line, and then count the number of integers that could be acceptable values of x.

Step 3: Approach Strategically

We can solve for the range of values that satisfy this inequality by isolating x, the same way we would for an equation. We must, however, do the same thing to all three parts. Subtracting 5 from all three parts, we get −4 < 3x < 12. We then divide all three parts by 3 to get .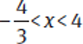

The integer values that satisfy this inequality are −1, 0, 1, 2, and 3. Therefore, there are five integer values, and the correct answer is (D).

Step 4: Confirm Your Answer

Confirm that your calculations are correct. Quickly sketch the range of x on a number line to confirm your count of the number of possible integer values of x.

15.   (E)

If b ≠ 0 and a > b, is a > c?

• (1)   

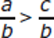
• (2)   5ab > 6bc

Step 1: Analyze the Question Stem

This is a Yes/No question. The question stem tells us that b ≠ 0 and a > b. We want to find out whether there is sufficient information to determine whether a > c. There is no information in the question stem that we can use to determine whether or not a > c, so let’s look at the statements.

Step 2: Evaluate the Statements Using 12TEN

Both of the statements are inequalities, so it’s important to remember that when we multiply both sides of an inequality by a positive number, the direction of the inequality sign stays the same, but when we multiply both sides of an inequality by a negative number, the direction of the inequality sign is reversed. Keeping this in mind, let’s look at the statements.

Begin with Statement (1), 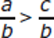. If b is positive, then multiplying both sides by b gives us a > c. But if b is negative, then multiplying both sides by b gives us a < c, since the sign of the inequality must be reversed. Therefore, Statement (1) does not tell us whether or not a is greater than c. Eliminate (A) and (D).

We can use the same logic when approaching Statement (2), 5ab > 6bc. If b is positive, then dividing both sides by b gives us 5a > 6c. If only 5 pieces of a is more than 6 pieces of c, a itself must be greater than c. However, if b is negative then dividing by b gives us 5a < 6c. In this instance a could be less than c, but it could also be greater than c. Thus, Statement (2) is insufficient. Eliminate (B).

When we put the two statements together, it is still necessary to know whether b is positive or negative in order to answer the question. Since we do not have this information, the statements taken together are insufficient and the correct answer is (E).

GMAT BY THE NUMBERS: ARITHMETIC

Now that you’ve learned how to approach arithmetic questions on the GMAT, let’s add one more dimension to your understanding of how they work.

Take a moment to try the following question. The next page features performance data from thousands of people who have studied with Kaplan over the decades. Through analyzing this data, we will show you how to approach questions like this one most effectively and how to avoid similarly tempting wrong answer choice types on Test Day.

What is the value of integer n?

• (1)  n = n⁴

• (2)  1ⁿ ≠ n

• Statement (1) ALONE is sufficient, but statement (2) is not sufficient.

• Statement (2) ALONE is sufficient, but statement (1) is not sufficient.

• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.

• EACH statement ALONE is sufficient.

• Statements (1) and (2) TOGETHER are NOT sufficient.

Explanation

This question combines your skill at dealing with exponents with your knowledge of number properties. You’re asked for the value of n and told only that it’s an integer. This leaves all integers as possible values—an important observation because some integers behave differently in certain arithmetic operations than others. 1, 0, and negative numbers all have special properties that are often crucial to identifying the right answer.

QUESTION STATISTICS

19% of test takers choose (A)

9% of test takers choose (B)

48% of test takers choose (C)

3% of test takers choose (D)

21% of test takers choose (E)

Sample size = 4,200

Statement (1) tells you that n = n⁴. It’s tempting to say immediately that n must equal 1, but there is another number that equals its own fourth power: 0. The question statistics reveal that test takers often overlook this possibility, so it’s no surprise that the testmaker creates questions for which doing so leads to a wrong answer, in this case choice (A). Since n could equal either 1 or 0, you cannot know its exact value, making Statement (1) insufficient.

Statement (2) tells you only that 1ⁿ ≠ n. No matter what exponent 1 is raised to, the value will remain 1. For example, 1² = 1, as do 1³ and 1⁴. So the only value of n that Statement (2) excludes is n = 1. Alone, this statement is certainly insufficient. But when combined with Statement (1), you have an answer. Statement (1) permits only n = 1 and n = 0. Statement (2) removes n = 1 from consideration, leaving n = 0 as the only possibility.

Considering unusual values, such as 0, will help you to avoid traps and rack up right answers. Also noteworthy is how many test takers select (E) on this problem. Such a response reflects a common error on difficult Data Sufficiency questions: these two statements are abstract, so many test takers—unsure of how to handle them—decide that they are insufficient. But this line of thinking equates “I’m not sure what to do” with “It can’t be done”—not an assumption that the GMAT rewards. Correct these common errors here in your prep, and you’ll see a much higher score on Test Day.

More GMAT by the Numbers …

To see more questions with answer choice statistics, be sure to review the full-length CATs in your online resources.