2
Watersheds and Flooding: a Segmentation Golden Braid

This book presents an in-depth analysis of watersheds and flooding in the abstract framework of weighted graphs. The reason for choosing these two topics is the popularity of marker-based watershed segmentation. Serge Beucher and Christian Lantuejoul were the first to use watersheds for segmenting objects (http://cmm.ensmp.fr/∼beucher/publi/watershed.pdf, [BEU 82]). If f is an image to be segmented, the watershed transform is applied to the modulus |∂f| of the gradient of f; the contours of the objects to be segmented appear as crest lines on this gradient image. The inside of the objects and the background appear as regional minima. Ideally, each object to be segmented would give rise to one regional minimum; the extension of the object itself would be the catchment zone of this minimum. In the real world, this ideal situation is rarely met, and many regional minima are present in the gradient image, especially if the initial image is textured or noisy. The watershed produce a partition in which each tile contains a regional minimum. The watershed partition then presents a severe oversegmentation. We proposed regularizing watersheds by introducing markers. The tiles of the resulting partition then contain one marker each with no oversegmentation. The contours of the objects follow the highest crest lines of the image between the markers. The resulting segmentation paradigm has been formalized in [MEY 90b, BEU 92]. Watersheds combined with markers constitute a powerful, yet simple segmentation method. Its power is due to the decoupling between the marking of the regions of interest and the contouring of these regions. The localization of the markers is the intelligent part of the process. Markers may be hand marked or automatically detected, depending on the application. Their shape or exact placement does not matter, which introduces robustness and flexibility in the method. For instance, it is sufficient to mark a few pixels in a 2D slice of a medical 3D CT scan to enable the contouring of the organs or tumors in a complete 3D volume. The method became especially popular after the publication of fast algorithms [VIN 91b, MEY 91].

It is impossible to make a review of the applications of watersheds to segmentation as they are simply too numerous. Several videos and tutorials about watershed segmentation are even available on YouTube. We will only give a few examples where the use of watersheds is less conventional.

For segmenting video images, the partition obtained for the current frame may be used for generating markers for the next frame. This has been used to automatically detect the carriage way in front of a running car [BEU 90b], or to segment video sequences in multimedia applications [ZAN 02a].

For complex images, the use of markers does not remove the obligation to filter the initial image before constructing its gradient and/or to filter the gradient image itself [KAR 06]. The quality of the result depends on the quality of the gradient, in particular for color or textured images [HIL 03, SHA 97, OGO 96]. The use of prior information facilitates the segmentation of complex scenes [GRA 04, LIN 03]. Recently, more and more sensors have become available, producing hyperspectral images on which watershed segmentation may also be successfully applied [TAR 10, ANG 09, ANG 10]. As explained in the primer on morphology, a watershed is also classically applied to separate overlapping cells in 2D images, or to separate the polyhedral cells in a 3D foam [CEN 94, KAM 15].

Initially, we will explain how the seminal ideas of Christian Lantuejoul have developed in many directions. We will then analyze the development of the other strand of watershed segmentation, namely flooding and, more generally, connected operators. This naturally leads to pyramids and hierarchies.

A catchment basin of a regional minimum is the set of nodes linked with a regional minimum through a runoff path, i.e. the trajectory of a drop of water. Such a drop of water evolves from node to node along a path of steepest descent. This evolution may be modeled by a node-weighted graph: the nodes of the graph are the pixels of the image, their weights are the gray tones, with neighboring pixels being linked by edges. In the next section, we study the interrelations between the catchment basins when they are filled by lakes. Adding a drop of water progresses from basin to basin through successive overflows. This type of evolution is then best described by edge-weighted graphs in which the nodes represent the catchment basins. Nodes are unweighted, whereas the edges, representing the pass points between adjacent basins, are weighted by the altitude of the pass point.

2.1. Watersheds, offsprings and parallel branches

A watershed, in its initial definition, is a natural continuation of the work done by Christian Lantuejoul on polycrystalline alloys. Indeed, a polycrystal results from the parallel germination and isotropic growth of crystals. The crystals cannot grow into each other, the growing of a crystal stops when meeting another crystal. Christian Lantuejoul modeled the polycrystal tessellation as a Voronoï tessellation. When the cells of the modeled tessellation are separated by a line, he called this line the skeleton by zones of influence or SKIZ [LAN 78]. When the crystals grow inside a hole, they form a geode. In contrast to the case where the crystals develop in free space, they are now constrained to follow the shape of the hole. For simulating this effect, Christian Lantuejoul developed a geodesic metric [LAN 81]. This geodesic metric is associated with a geodesic SKIZ.

In the same line of thought, a watershed partition may be considered as the result of the growth of lakes, fed by sources placed at the position of regional minima. The lakes, like the crystals are prevented to merge, creating a partition of basins. However, the crystals grow with a uniform speed in space, and the depth of the lakes grows with a uniform speed but not their spatial extension. Christian Lantuejoul and Serge Beucher have defined a flooding scheme with the same behavior. A geodesic SKIZ of the regional minima is constructed level-by-level, inside the successive lower thresholds of the topographic surface (the thresholds of the holes of the surface). Thus, the lakes grow in extension in each binary threshold and when the geodesic SKIZ is completed in one threshold, it serves as seed for a new geodesic SKIZ in the next threshold. This scheme also makes it possible to flood the surface starting from a set of markers, by replacing the regional minima with markers. This first watershed algorithm has been implemented on the first prototype of the texture analyzer developed by Jean Claude Klein [KLE 76]. The SKIZ was implemented through Golay-type operators [PRE 79], making it possible to produce homotopic thinnings or thickenings [SER 82]. Later, Gilles Bertrand proposed a “topological watershed”, a watershed construction based on gray tone thinnings, in which the altitude of pixels is lowered if it does not change the homotopy [BER 05].

See also in [COU 09a] and [NAJ 13] a connection between the topological watershed and a definition of the watershed based on the evolution of a drop of water on edge weighted graphs, but without establishing a link with node weighted graphs. One of the main contribution of this book is to establish the equivalence between node weighted and edge weighted graphs with respect to the watershed and to floodings.

The development of affordable general-purpose computers, with enough memory to hold gray tone images, triggered the development of new generations of algorithms. By providing random access to the images, they enable us to implement the shortest-distance algorithm of Moore Dijkstra [MOO 57]. This algorithm progressively expands the domain S for which the distance is known and estimates the shortest distance of the neighboring nodes of S. The node with the shortest estimated distance may then be introduced into S. Luc Vincent used a waiting queue for storing the addresses of the neighbors of S [VIN 92, BRE 94]. If in addition the seeds are labeled and propagated along the geodesics of the distance function, we obtain a SKIZ.

This algorithm was much faster than the algorithms based on thickenings. It was straightforward to introduce it in the watershed algorithm of Christian Lantuejoul and Serge Beucher. Luc Vincent and Pierre Soille proposed a clever way to generate the successive lower thresholds of an image and published an extremely popular and widely used watershed algorithm [VIN 91a].

The watershed algorithm extends the flooded region according to a dual order: in each threshold, the flooding progresses with an increasing distance to the lower border of this threshold. Since the flood level increases uniformly, lower pixels are flooded before higher ones, which impose a second-order relation. The flooding progression may thus be scheduled using a hierarchical queue, i.e. a series of prioritized queues. The priority level of each queue enables us to respect the second-order relation between the gray tone levels, the queues with the highest priority storing the lowest pixels. Each queue, used in the first-in first-out mode, enables us to implement the correct flood progression in each threshold. This algorithm first published in 1991 [MEY 91] unveiled its qualities only progressively [LOT 02]. In fact, it implements not only a dual order relation but also a lexicographic order relation measuring the steepness of the geodesics of the distance function [MEY 15c].

A new milestone has been met when the watershed partition has been defined as a Voronoï tessellation for a particular distance, whose geodesics are precisely the paths of steepest descent. Laurent Najman and Michel Schmitt defined it in the continuous space [NAJ 94b] and Fernand Meyer in the digital space [MEY 94b]. It appeared that the algorithm developed for implementing a dual order relation takes over without modifying the new definition [MEY 91]. If we take into account larger neighborhoods, it may be transformed into a Chamfer distance transform, as defined by Gunila Borgefors for digital distances [BOR 86]. We may also use more sophisticated methods to compute distances [PEY 10]. An implementation on graphic processors (gpu) has been proposed in [KAU 08].

A critical review of several definitions of the watershed transform and the associated sequential algorithms has been given in [ROE 00] along with a discussion of parallelization strategies. It has been incorporated into an energy-driven watershed algorithm in [NGU 03].

In a continuous formulation, the topographic distance of f along a path becomes the line integral of ||∇ f|| along this path. Viewing the domain of f as a 2D optical medium with a refractive index η (x, y) = ||∇ f|| makes the continuous topographic distance function equivalent to the optical path length which is proportional to the time required for light to travel this path. This leads to the eikonal PDE ||∇ U(x, y)|| = η (x, y) with η (x, y) = ||∇f (x, y)|| whose solution for any field η (x, y) is a weighted distance transform.

Formulating the watershed transform as the solution to the eikonal equation opens the door to powerful numerical algorithms for solving PDE using curve evolution [MAR 98, OSH 88] or via hardware implementations [NGU 03].

The geodesics of the topographical distance are relatively selective and the number of pixels linked with two distinct regional minima is rare. For this reason, the catchment zones may overlap, but not too much. Hence, it is possible to represent the geodesic piecewise: each pixel is linked by an edge to its lowest neighbors, since a geodesic path of the topographic distance passes through this edge. Thus, we obtain a “watershed graph”. This representation was first introduced by Francis Maisonneuve [MAI 80]. He was also the first to use inside the plateaus the geodesic distance to their lower border. Thus, each node without a lower neighbor for the relief has a lower neighbor for this distance function.

With the introduction of these edges, watershed basins become connected subgraphs of the watershed graph (some heuristics enable us to break the tiles for the few pixels still belonging to two watershed basins). Being a labeling problem, it may also be solved in hardware [LEM 96]. The same representation also enables a parallel construction of watershed partitions [MOG 97, BIE 00].

One of the weaknesses of watersheds is that they are prone to leaks during the flooding process for constructing the watershed partition. A blurred image may lead locally to low gradient values, unable to contain the flooding, leaking from one basin to the next. The viscous watershed transform enables us to robustify the watershed localization in the presence of leaks. It is like using a viscous fluid for flooding; the image is filtered so that the classical flooding process progresses on the filtered image as would a viscous flood on the original image [VAC 07, MAR 08].

2.2. Flooding and connected operators

Flooding allows regional minima to disappear, filling holes, and thus regularizing watershed segmentation: a catchment zone filled by a full lake is absorbed by a neighboring basin. The first flooding operators and their dual counterpart were first developed for binary images, which is called “reconstruction closings” and “reconstruction openings”. We proposed the first reconstruction opening, implemented as the first iterative algorithm in the prototype of the texture analyzer, a hardwired image processing device developed at the Centre for Mathematical Morphology (CMM) [KLE 76]. We used it for eliminating the masks of the cells of large size in a binary image. The large cells are those which are not completely suppressed after an erosion. If the initial image is a set X and the markers obtained by erosion is a set Y, the reconstruction opening of X from Y is the result of iterating the operation Y = δY ∩ X, where δY is the elementary dilation of Y. At each step, Y is enlarged by the dilation, while remaining within X through the intersection with X [MEY 79].

Reconstruction openings completely reconstruct some particles and discard others. Reconstruction closings completely fill holes and discard others. The extension to gray tone functions is straightforward, replacing the binary dilation by a gray tone dilation and the intersection between sets by the infimum between functions [SER 82] and [VIN 93b]. The gray tone reconstruction opening of a function f from a function g ≤ f may be analyzed level-by-level: the connected particles of the threshold {f > λ} touching the threshold {g > λ} are kept, and all others are eliminated. The global effect on the gray tone function is to produce a razing effect.

The common feature of these operators is to never create new contours. The result of a binary reconstruction opening is a subset of the initial particles, with unmodified contours. The contours of the suppressed particles have vanished. Hence, these operators are called connected operators. They are easily characterized: two neighboring pixels p and q are not separated by a contour for a function f, if f_p = f_q (f_p stands for f(p)). A function g is then the result of a connected operator applied to f if and only if {f_p = f_q} ⇒ {g_p = g_q} for all couples of neighboring pixels p and q. The maximal connected particles verifying f_p = f_q on any couple of inside neighboring nodes are called flat zones. Any binary and symmetrical relation between neighboring pixels is associated with an arcwise connectivity through the following equivalence relation 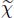: two pixels x and y are equivalent if a path linking x and y exists (a series of pixels starting at x, ending at y, such that two consecutive pixels are neighbors), such that the relation χ holds between two consecutive pixels of the path. It is easy to verify that if the relation χ is symmetrical and reflexive, then 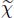is an equivalence relation. If {x χ y} ⇔ {f_x = f_y}, the equivalence classes of 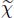are the flat zones of f. If {x θ y} ⇔ {|f_x – f_y| < λ}, the equivalence classes of 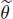are called λ – flat zones.

Connected operators have been intensively studied, as they enable us to simplify images without creating new contours [CRE 93, CRE 95, HEI 97, SAL 95] highlighting the links between connected operators and reconstruction openings and closings. Openings or razings are anti-extensive (clip peaks), whereas closings or floodings are extensive (fill valleys). When iterated, they form morphological filters [MAT 88a] and [MAT 88b], while remaining connected operators, acting both on peaks and valleys. However, the product of flooding and razing is generally not commutative.

Levelings, on the contrary, are strong filters [MAT 88b] and may be expressed as a commutative product of flooding and razing. The criterion {f_p = f_q} ⇒ {g_p = g_q} becomes by contraposition {g_p ≠ g_q} ⇒ {f_p ≠ f_q} and characterizes all connected operators. Levelings form a subclass of connected operators verifying {g_p < g_q} ⇒ {f_p < g_p ≤ g_q ≤ f_q}. It turns out that razings are anti-extensive levelings characterized by {g_p < g_q} ⇒ {f_p = g_p} and g = f ∧ δg; by duality, floodings are extensive levelings characterized by {g_p < g_q} ⇒ {f_q = g_q} and g = f ∨ εg [MEY 98a, MAT 97, MEY 98b, HEI 01, KRE 98, MEY 10a].

Levelings may also be characterized by a partial differential equation (PDE) expressing how a marker function g evolves towards the leveling of the function f, behaving as a dilation of g wherever g < f and as an erosion of g wherever g > f [MAR 99, MAR 00].

Many selection criteria for keeping or eliminating connected particles in a binary image are possible, for instance, keeping all particles with an area above some value n. The result is an area opening. Repeating the same operation on the thresholds of a gray tone image clips until a plateau is reached with an area above the threshold n [VIN 93a]. Various tree representations of images have been introduced and may be pruned according to various criteria to produce leveling. The max-tree (respectively min-tree) represents the successive lower (respectively upper) thresholds as a tree, starting with the regional maxima (respectively minima) as leaves. These trees may be pruned according to various criteria and cause flooding for the min-tree or razing for the max-tree [OLI 96, SAL 09]. Both trees may be combined in a tree of shapes which may be pruned and generate leveling [MON 00, CAS 08].

In the case of color images, each color component may be leveled separately, with the risk to producing false colors, not present in the initial image. Vectorial levelings consider the geometry of the color space as a whole and not through the color components [GOM 99, MEY 02a, ZAN 02b]. More general connections than the arcwise connectivity have been defined in [SER 96, SER 00].

2.3. Connected operators and hierarchies

Connected operators may be cascaded, with the concatenation of connected operators still being a connected operator. From each operator to the next, new flat zones are merged, forming a pyramid of flat zones. The basis of the pyramid contains all flat zones of the initial image, and the successive levels contain less and less flat zones. From one level to the next, only fusions of flat zones take place [SER 93, SAL 98].

Multicriteria mergings may be represented in the form of the binary partition tree. This tree may then be pruned in order to extract objects with particular features [SAL 00, VIL 08].

The algebraic structure of such a pyramid is called a hierarchy. A hierarchy is a collection of sets on which an order relation is defined. A set A is said to be the predecessor of a set B in the hierarchy if B ⊊ A. This collection of sets forms a hierarchy or dendrogram if the predecessors of each set are well ordered for the inclusion [BEN 73, BEN 72, JAR 71]. A stratification index st on the dendrogram distinguishes the several levels of the hierarchy, it verifies {A ⊂ B, A ≠ B} ⇒ st(A) < st(B). The stratification index in turn enables us to define an ultrametric distance ζ between the leaves of the dendrogram. If A and B are two leaves of the dendrogram, the ultrametric distance ζ(A, B) is the stratification index of the smallest set of the dendrogram containing both A and B. If no such set exists, it is equal to ∞. The distance verifies the ultrametric inequality ζ(A, B) ≤ ζ(A, C) ∨ ζ(C, B), since ζ(A, C) ∨ ζ(C, B) represents the stratification index of the smallest set of the dendrogram containing all three sets A, B and C.

The most famous dendrogram is the classification of the species by Linné. Dendrograms are a fundamental tool for taxonomy and classification [KRA 47, GON 76, GON 95, LEC 81].

Dendrograms are pertinent to the framework of segmentation as they enable us to express multiscale segmentations. It often happens that the first segmentation produces a partition on which a dissimilarity between adjacent regions has been defined. This dissimilarity may be based on any cues, as color, local gradient, texture, etc. This situation may be modeled by an edge-weighted graph in which the nodes represent the regions of the fine segmentation. Two neighboring regions are linked by an edge weighted by the dissimilarity between them.

A dendrogram is then naturally derived. The successive levels of the dendrogram are simply obtained by merging all neighboring regions with a dissimilarity between a given threshold n. Two regions A and B will belong to the same region after these mergings if they are linked by a path whose edges have a dissimilarity below n or equal to n. By increasing the value n, more and more regions are merged, forming a dendrogram. The associated ultrametric distance between two leaves A and B of the dendrogram is the lowest dissimilarity value n at which they will be merged into a unique connected set. Thus, they appear as general edge-weighted graphs whose topography will be studied in this book.

A powerful method for estimating the dissimilarity of adjacent regions is the stochastic watershed. The seminal idea, introduced by Jesus Angulo [ANG 07, ANG 09], is to spread random germs all over the image and to use them as markers for watershed segmentation. Large regions, separated by low contrast gradient from neighboring regions, will be sampled more frequently than smaller regions and will be selected more often. On the contrary, strong contours will often be selected by watershed construction, as there are many possible positions of markers which will select them. Evaluating the strength of the contours by simulation offers a great versatility: various laws for the implementation of point patterns, and various shapes for the markers themselves may be used. The method suffers, however, from a serious handicap, if the contour strength is evaluated through simulations, as each of them requires the construction of a watershed segmentation. We show in [MEY 10b, MEY 15a], not only how simulations may be avoided, but also how to imagine scenarios which would be difficult or even impossible to simulate.

Yet, the most common hierarchy is the one associated with any relief: the leaves are the regions of a watershed partition, the edges linking two neighboring regions are weighted by the pass point that makes it possible to pass from one catchment zone to the other in the topographical surface.

2.4. Hierarchical segmentation: extinction values

The two preceding sections have treated watershed construction and the connected operators separately. In this last section, we present how, together, they generate new concepts. The hierarchies linked to connected operators involve the flat zones: a connected operator applied to an image merges flat zones. With cascaded connected operators, an increasing number of flat zones merge, forming the successive levels of the dendrogram.

In this last section, we show how flooding or leveling interferes with a watershed producing new types of hierarchies. We have remarked in the primer that a lake partially filling a catchment zone may be either a regional minimum lake or a full lake. If it is a regional minimum lake, its level increases by adding a drop of water. If it is a full lake, adding a drop of water provokes an overflow into a neighboring basin, and a watershed partition of the flooded relief will merge the basins of the initial surface. A lake may also cover several regional minima of the topographic surface, it then belongs to a unique catchment zone. Whether a lake overflows when adding a drop of water does not depend on the precise form of the topographic surface under and around the lake, but only on the altitude of the pass points between adjacent catchment zones. These inter relations are best modeled by an edge-weighted graph, in which the nodes represent the catchment zones and the edges between adjacent catchment zones are weighted by the altitude of the pass point that makes it possible to pass from one to another. This edge-weighted graph is called the region adjacency graph.

This shows that a flowing topographic surface produces a coarser watershed partition, since regions of the initial partition have merged. For increasing flooding levels, the process repeats, and the watershed partitions become increasingly coarse. The series of watershed partitions associated with increasing flooding of a topographic surface thus form a hierarchy [MEY 02b, MEY 01].

Levelings do not create regional minima or maxima. If a function g is the leveling of a function f, and X is a regional minimum (respectively maximum) of g, then X contains one or several regional minima (respectively maxima) of f. Thus, applying successive levelings (and floodings are particular levelings) to an image, the resulting image has decreasing minima, and its watershed partition gets coarser, by fusion of regions of the previous watershed partition [MEY 04]. Successive levelings and their derived watershed partitions form a scale space structure: the partitions get coarser at each step. In addition, each region at a given level is the union of regions at the previous levels.

When the successive floodings depend on a scale parameter, the resulting hierarchies carry a particular meaning. This is the case when floodings are the highest for an image under increasing ceiling functions. If the ceiling function is obtained by adding a constant to the initial image, floodings create lakes with increasing depth. The less contrasted regions are the first to disappear. It is then possible to weigh each regional minimum and each piece of contour of a fine partition by the scale index for which this regional minimum disappears in the flooded surface and this contour disappears in the associated watershed partition. This value has been called dynamics of the minimum or of the contour [NAJ 96, NAJ 94a, BER 07, MEY 96], in the case where flooding expands lakes by increasing depth. Flooding may also expand lakes by increasing surfaces or volumes [VAC 95a, VAC 95b]. They are then called surface associated extinction values or volume associated extinction values. More generally, extinction values may be associated with each series of increasing flooding.

The dynamics or contrast associated extinction value has first been introduced by Michel Grimaud for weighting the micro calcification in a mammography according to their contrast [GRI 91, GRI 92].

PDE solutions also exist combining size-driven flooding and watershed as in [SOF 08, SOF 03, SOF 05].

Flooding and leveling may be directly computed on the region adjacency graph [MEY 07b]. Marker-based segmentation may also be directly computed on this graph [MEY 94a].

A particular flooding, called the waterfall flooding, is easily represented on the region adjacency graph. A weight is assigned to the nodes, representing the level of the flooding in each node. The waterfall flooding floods the topographic surface at the maximum possible level before overflows occur: each watershed basin is filled up to its lowest pass point leading to another basin. Adding a drop of water to a lake provokes a series of cascades, from lake to lake until reaching a regional minimum lake. This flooded surface has much less regional minima than the initial surface and its catchment zones are unions of catchment zones of the initial surface. The same flooding process may then be repeated on the already flooded surface and still produces less watershed basins [BEU 94, BEU 11]. It may be directly computed on the image or on its region neighborhood graph [MAR 05, MEY 15b, MEY 12, GOL 14]. As the waterfall hierarchy is independent of any parameter, it is widely used for simplifying segmentations [HAN 06, DEL 06, ANG 03, ANG 09].