Karl Marx’s mathematical papers, to which Engels attached so much importance, but which he did not live to publish, were printed by the Soviet philosophical review, Pod Znamenem Marksizma, in the issue of January-February 1933. As I had never seen any discussion of them, I submitted them to one of the most distinguished of American mathematicians, who has kindly sent me the following report.
The three articles on mathematics by Marx appear to be the notes of an intelligent (but somewhat befuddled) beginner, who is just starting to understand the meaning of differentiation. I doubt whether they were ever intended as a serious contribution to mathematics.
Marx seems to be dealing, in the main, with the differentiation of a function,
in the very simple case where f(x) is an ordinary polynomial. Suppose we give x an increment Δx. Then the corresponding increment of y is
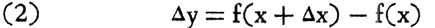
Therefore, if we divide both sides of (2) by Δx, we get
Now, if f(x) is an ordinary polynomial in x, the expression f(x + Δx) — f(x) is an ordinary polynomial in x and Δx. Moreover, we easily verify that all terms cancel out from f(x + Δx) — f(x) except the ones having Δx as a factor. Therefore, the expression can be written in the form
f(x + Δx) — f(x) = Δx. φ (x, Δx)
If we substitute the last expression in the right hand member of (3) and cancel Δx in numerator and denominator, we get
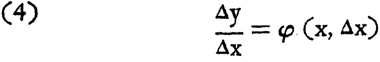
Finally, if we set Δx = o in (4), (whence, also Δy = 0), we get an expression of the form
In other words, we arrive at the following “paradox.” The left hand member of (5) is the meaningless expression 
; yet, lo, and behold, the right hand member has a definite meaning, and turns out, in fact, to be the desired derivative of f(x)!
You can see that a paradox like the above is duck soup for a dialectical materialist and can give rise to long discussions about thesis, antithesis, the negation of the negation, etc., etc., etc. On all of this, I am incapable of expressing any opinion. To me, it is just so much metaphysical mumbo-jumbo. The straightforward mathematical explanation is elementary and requires no philosophical soaring. It is simply this:
If the expression A = B is true, you can conclude that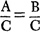 
is also true provided that C does not vanish. If C vanishes, the second equation is, in general, quite meaningless.* Consequently, Equation (3) can only be expected to follow from Equation (2) for values of Δx different from o, and we must not be surprised to get a meaningless result (5) when we set Δx = o in (3). Now, how does it happen that, in spite of all this, the right hand member of (5) actually is the derivative of f(x)? Well, simply this. The derivative of f(x) is, by definition, the value approached by 
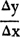as Δx approaches o. (The value approached has a definite meaning, although the value at Δx = o has none.) Moreover, the right hand member of (4) (which equals the left hand member for all values of Δx except o) is an ordinary polynomial and, therefore (unlike the left hand member), has a definite value even for Δx = o. Moreover, since a polynomial is continuous, the value approached as Ax approaches zero is identical with the value at Δx = o. Therefore, φ (x, o) is the desired derivative.
In conclusion, let me say that there is nothing new that I can see, in the mathematical side of the three papers by Marx.
I have tried on numerous occasions to fathom the mysteries of dialectical materialism and have each time been left baffled and bewildered. Engels has a section on mathematics in his famous Anti-Dühring (which is supposed to echo the voice of the Master himself). Unfortunately, the mathematics itself is all cock-eyed. It is a pity to build an elaborate philosophical system on a series of gross mathematical errors.
* “Division by zero” leads to obviously false results. Indeed, 1 X 0 = 2 X 0 is a true equation, since both members vanish. But we obviously cannot strike out the factor o on both sides and conclude 1 = 2.