Chapter 1

Preliminaries and Basic Operations

Chapter Check-In

Categories of numbers

Properties of addition and multiplication

Powers and exponents

Square roots and cube roots

Parentheses, brackets, and braces

Divisibility rules

Before you begin learning, relearning, or reviewing algebra, you need to feel comfortable with some pre-algebra terms and operations. This chapter starts with some basic essentials.

Preliminaries

The first items you should become familiar with are the different categories or types of numbers and the common math symbols.

Categories of numbers

In doing algebra, you work with several categories of numbers.

• Natural or counting numbers. The numbers 1, 2, 3, 4, . . . are called natural or counting numbers.

• Whole numbers. The numbers 0, 1, 2, 3, . . . are called whole numbers.

• Integers. The numbers . . . –2, –1, 0, 1, 2, . . . are called integers.

• Negative integers. The numbers . . . –3, –2, –1 are called negative integers.

• Positive integers. The natural numbers are sometimes called the positive integers.

• Rational numbers. Fractions, such as or , are called rational numbers. Since a number such as 5 may be written as , all integers are rational numbers. All rational numbers can be written as fractions 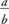, with a being an integer and b being a natural number. Terminating and repeating decimals are also rational numbers, because they can be written as fractions in this form.

• Irrational numbers. Another type of number is an irrational number. Irrational numbers cannot be written as fractions 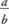, with a being an integer and b being a natural number. 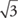and π are examples of irrational numbers. An irrational number, when exactly expressed as a decimal, neither terminates nor has a repeating decimal pattern.

• Even numbers. Even numbers are integers divisible by 2: … –6, –4, –2, 0, 2, 4, 6, …

• Prime numbers. A prime number is a natural number that has exactly two different factors, or that can be perfectly divided by only itself and 1. For example, 19 is a prime number because it can be perfectly divided by only 19 and 1, but 21 is not a prime number because 21 can be perfectly divided by other numbers (3 and 7). The only even prime number is 2; thereafter, any even number may be divided perfectly by 2. Zero and 1 are not prime numbers or composite numbers. The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.

• Odd numbers. Odd numbers are integers not divisible by 2: …–5, –3, –1, 1, 3, 5,….

• Composite numbers. A composite number is a natural number divisible by more than just 1 and itself: …4, 6, 8, 9,…

• Squares. Squares are the result when numbers are multiplied by themselves, that is, raised to the second power. 2 · 2 = 4; 3 · 3 = 9. The first six squares of natural numbers are 1, 4, 9, 16, 25, 36.

• Cubes. Cubes are the result when numbers are multiplied by themselves and then again by the original number, that is, raised to the third power. 2 · 2 · 2 = 8; 3 · 3 · 3 = 27. The first six cubes of natural numbers are 1, 8, 27, 64, 125, 216.

Ways to show multiplication

There are several ways to show multiplication of a pair of numerical values.

• When the two numerical values are known, you can show the multiplication of 4 with 3 as follows:

4 × 3

4 · 3

(4)(3)

4(3)

(4)3

• When one value is a number and the other value is a variable: show multiplication of 4 and a as follows:

4 × a

4 · a

(4)(a)

4(a)

(4)a

4a

• When both values are variables: show the multiplication of a and b as follows:

a × b

a · b

(a)(b)

a(b)

(a)b

ab

Common math symbols

The following math symbols appear throughout algebra. Be sure to know what each symbol represents.

Symbol references:

= is equal to

≠ is not equal to

> is greater than

< is less than

≥ is greater than or equal to (also written )

≤ is less than or equal to (also written )

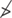is not greater than

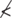is not less than

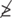is not greater than or equal to

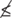is not less than or equal to

≈ is approximately equal to (also )

Properties of Basic Mathematical Operations

Some mathematical operations have properties that can make them easier to work with and can actually save you time.

Some properties (axioms) of addition

You should know the definition of each of the following properties of addition and how each can be used.

• Closure is when all answers fall into the original set. If you add two even numbers, the answer is still an even number (2 + 4 = 6); therefore, the set of even numbers is closed under addition (has closure). If you add two odd numbers, the answer is not an odd number (3 + 5 = 8); therefore, the set of odd numbers is not closed under addition (no closure).

• Commutative means that the order does not make any difference in the result.

2 + 3 = 3 + 2

a + b = b + a

Note: Commutative does not hold for subtraction.

3 – 1 ≠ 1 – 3

2 ≠ –2

a – b ≠ b – a

• Associative means that the grouping does not make any difference in the result.

(2 + 3) + 4 = 2 + (3 + 4)

(a + b) + c = a + (b + c)

The grouping has changed (parentheses moved), but the sides are still equal.

Note: Associative does not hold for subtraction.

4 – (3 – 1) ≠ (4 – 3) – 1

4 – 2 ≠ 1 – 1

2 ≠ 0

a – (b – c) ≠ (a – b) – c

• The identity element for addition is 0. Any number added to 0 gives the original number.

3 + 0 = 0 + 3 = 3

a + 0 = 0 + a = a

• The additive inverse is the opposite (negative) of the number. Any number plus its additive inverse equals 0 (the identity).

3 + (–3) = 0; therefore, 3 and –3 are additive inverses.

–2 + 2 = 0; therefore, –2 and 2 are additive inverses.

a + (–a) = 0; therefore, a and –a are additive inverses.

Some properties (axioms) of multiplication

You should know the definition of each of the following properties of multiplication and how each can be used.

• Closure is when all answers fall into the original set. If you multiply two even numbers, the answer is still an even number (2 × 4 = 8); therefore, the set of even numbers is closed under multiplication (has closure). If you multiply two odd numbers, the answer is an odd number (3 × 5 = 15); therefore, the set of odd numbers is closed under multiplication (has closure).

• Commutative means the order does not make any difference.

2 × 3 = 3 × 2

a × b = b × a

Note: Commutative does not hold for division.

2 ÷ 4 ≠ 4 ÷ 2

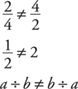
• Associative means that the grouping does not make any difference.

(2 × 3) × 4 = 2 × (3 × 4)

(a × b) × c = a × (b × c)

The grouping has changed (parentheses moved) but the sides are still equal.

Note: Associative does not hold for division.

(8 ÷ 4) ÷ 2 ≠ 8 ÷ (4 ÷ 2)

2 ÷ 2 ≠ 8 ÷ 2

1 ≠ 4

(a ÷ b) ÷ c ≠ a ÷ (b ÷ c)

• The identity element for multiplication is 1. Any number multiplied by 1 gives the original number.

3 × 1 = 1 × 3 = 3

a × 1 = 1 × a = a

• The multiplicative inverse is the reciprocal of the number. Any nonzero number multiplied by its reciprocal equals 1.

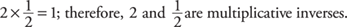
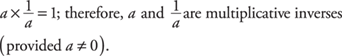
A property of two operations

The distributive property is the process of passing the number value outside of the parentheses, using multiplication, to the numbers being added or subtracted inside the parentheses. In order to apply the distributive property, it must be multiplication outside the parentheses and either addition or subtraction inside the parentheses.

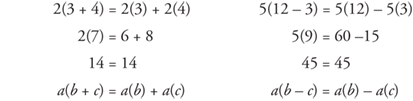
Note: You cannot use the distributive property with only one operation.

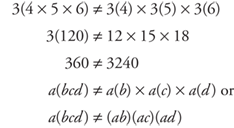
Multiplying and Dividing Using Zero

Zero times any number equals zero.

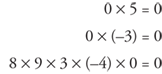
Likewise, zero divided by any nonzero number is zero.

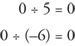
Important note: Dividing by zero is “undefined” and is not permitted.

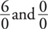are not permitted.

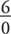has no answer and does not have a unique answer.

In neither case is the answer zero.

Powers and Exponents

An exponent is a positive or negative number placed above and to the right of a quantity. It expresses the power to which the quantity is to be raised or lowered. In 4³, 3 is the exponent and 4 is called the base. It shows that 4 is to be used as a factor three times. 4 × 4 × 4 (multiplied by itself twice). 4³ is read as four to the third power (or four cubed as discussed later in this chapter).

24 = 2 × 2 × 2 × 2 = 16

3² = 3 × 3 = 9

Remember that x1 = x and x0 = 1 when x is any number (other than 0).

If the exponent is negative, such as 3–2, then the base can be dropped under the number 1 in a fraction and the exponent made positive. An alternative method is to take the reciprocal of the base and change the exponent to a positive value.

Example 1: Simplify the following by changing the exponent from a negative value to a positive value and then evaluate the expression.

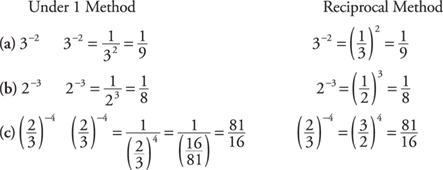
Squares and cubes

Two specific types of powers should be noted, squares and cubes. To square a number, just multiply it by itself (the exponent would be 2). For example, 6 squared (written 62) is 6 × 6, or 36. 36 is called a perfect square (the square of a whole number). Following is a list of the first twelve perfect squares:

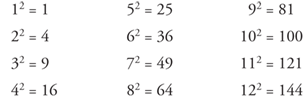
To cube a number, just multiply it by itself twice (the exponent would be 3). For example, 5 cubed (written 53) is 5 × 5 × 5, or 125. 125 is called a perfect cube (the cube of a whole number). Following is a list of the first twelve perfect cubes.

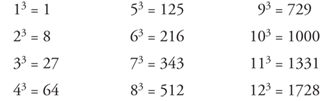
Operations with powers and exponents

To multiply two numbers with exponents, if the base numbers are the same, simply keep the base number and add the exponents.

Example 2: Multiply the following, leaving the answers with exponents.

(a) 23 × 25 = 28    (2 × 2 × 2) × (2 × 2 × 2 × 2 × 2) = 28

(b) 32 × 34 = 36    (3 × 3) × (3 × 3 × 3 × 3) = 36

To divide two numbers with exponents, if the base numbers are the same, simply keep the base number and subtract the second exponent from the first, or the exponent of the denominator from the exponent of the numerator.

Example 3: Divide the following, leaving the answers with exponents.

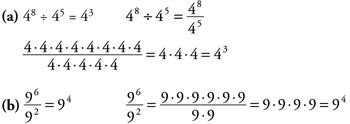
To multiply or divide numbers with exponents, if the base numbers are different, you must simplify each number with an exponent first and then perform the operation.

Example 4: Simplify and perform the operation indicated.

(a) 32 × 22 = 9 × 4 = 36

(b) 62 ÷ 23 = 36 ÷ 8 =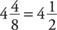

(Some shortcuts are possible.)

To add or subtract numbers with exponents, whether the base numbers are the same or different, you must simplify each number with an exponent first and then perform the indicated operation.

Example 5: Simplify and perform the operation indicated.

(a) 32 – 23 = 9 – 8 = 1

(b) 43 + 32 = 64 + 9 = 73

If a number with an exponent is raised to another power (42)3, simply keep the original base number and multiply the exponents.

Example 6: Multiply and leave the answers with exponents.

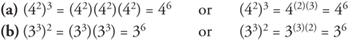
Square Roots and Cube Roots

Note that square and cube roots and operations with them are often included in algebra sections, and both topics are discussed more in Chapter 11.

Square roots. To find the square root of a number, you want to find some number that when multiplied by itself gives you the original number. In other words, to find the square root of 25, you want to find the number that when multiplied by itself gives you 25. The square root of 25, then, is 5. The symbol for square root is 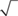. Following is a list of the first eleven perfect (whole number) square roots.

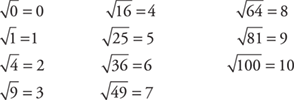
Special note: If no sign (or a positive sign) is placed in front of the square root, then the positive answer is required. Only if a negative sign is in front of the square root is the negative answer required. This notation is used in many texts and is adhered to in this book. Therefore,

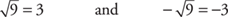
Cube roots

To find the cube root of a number, you want to find some number that when multiplied by itself twice gives you the original number. In other words, to find the cube root of 8, you want to find the number that when multiplied by itself twice gives you 8. The cube root of 8, then, is 2, because 2 × 2 × 2 = 8. Notice that the symbol for cube root is the radical sign with a small three (called the index) above and to the left 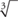. Other roots are defined similarly and identified by the index given. (In square root, an index of two is understood and usually not written.) Following is a list of the first eleven perfect (whole number) cube roots.

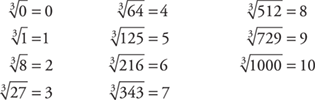
Approximating square roots

To find the square root of a number that is not a perfect square, it will be necessary to find an approximate answer by using the procedure given in Example 7.

Example 7: Approximate .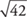

Since 62 = 36 and 72 = 49, then 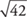is between 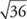and .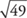

Therefore, 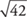is a value between 6 and 7. Since 42 is about halfway between 36 and 49, you can expect that 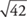will be close to halfway between 6 and 7, or about 6.5. To check this estimation, 6.5 × 6.5 = 42.25, or about 42.

Square roots of nonperfect squares can be approximated, looked up in tables, or found by using a calculator. You may want to keep these two in mind:

Simplifying square roots

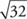Sometimes you will have to simplify square roots, or write them in simplest form. In fractions, can be reduced to . In square roots, can be simplified to .

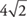There are two main methods to simplify a square root.

Method 1: Factor the number under the 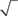into two factors, one of which is the largest possible perfect square. (Perfect squares are 1, 4, 9, 16, 25, 36, 49, …)

Method 2: Completely factor the number under the 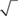into prime factors and then simplify by bringing out any factors that came in pairs.

Example 8: Simplify .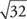

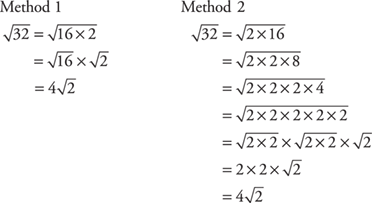
In Example 8, the largest perfect square is easy to see, and Method 1 probably is a faster method.

Example 9: Simplify .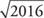

In Example 9, it is not so obvious that the largest perfect square is 144, so Method 2 is probably the faster method.

Many square roots cannot be simplified because they are already in simplest form, such as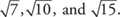

Grouping Symbols

There are basically three types of grouping symbols: parentheses, brackets, and braces.

Parentheses ( )

Parentheses are used to group numbers or variables. Everything inside parentheses must be done before any other operations.

Example 10: Simplify.

50(2 + 6) = 50(8) = 400

When a parenthesis is preceded by a minus sign, to remove the parentheses, change the sign of each term within the parentheses.

Example 11: Simplify.

6 – (–3 + a – 2b + c) =

6 + 3 – a + 2b – c =

9 – a + 2b – c

Brackets [ ] and braces { }

Brackets and braces also are used to group numbers or variables. Technically, they are used after parentheses. Parentheses are to be used first, then brackets, and then braces: {[( )]}. Sometimes, instead of brackets or braces, you will see the use of larger parentheses.

((3 + 4) · 5) + 2

A number using all three grouping symbols would look like this:

2{1 + [4(2 + 1) + 3]}

Example 12: Simplify 2{1 + [4(2 + 1) + 3]}. Notice that you work from the inside out.

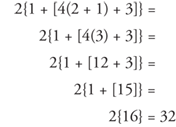
Order of operations

If multiplication, division, powers, addition, parentheses, and so forth are all contained in one problem, the order of operations is as follows:

1. Parentheses

2. Exponents (or radicals)

3. Multiplication or division (in the order it occurs from left to right)

4. Addition or subtraction (in the order it occurs from left to right)

Many students find the made up word PEMDAS helpful as a memory tool. The “P” reminds you that “parentheses” are done first; the “E” reminds you that “exponents” are done next; the “MD” reminds you to “multiply or divide” in the order it occurs from left to right; and the “AS” reminds you to “add or subtract” in the order it occurs from left to right.

Also, some students remember the order using the following phrase:

Please Excuse My Dear Aunt Sally

Parentheses Exponents Multiply or Divide Add or Subtract

Example 13: Simplify the following problems.

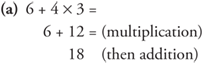
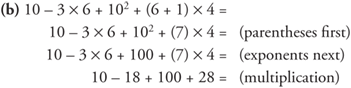
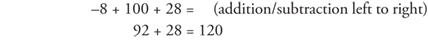
Divisibility Rules

The following set of rules can help you save time in trying to check the divisibility of numbers.

A number is divisible by	if
2	it ends in 0, 2, 4, 6, or 8
3	the sum of its digits is divisible by 3
4	the number formed by the last two digits is divisible by 4
5	it ends in 0 or 5
6	it is divisible by 2 and 3 (use the rules for both)
7	(no simple rule)
8	the number formed by the last three digits is divisible by 8
9	the sum of its digits is divisible by 9

Example 14:

(a) Is 126 divisible by 3? Sum of digits = 9. Because 9 is divisible by 3, then 126 is divisible by 3.

(b) Is 1,648 divisible by 4? Because 48 is divisible by 4, then 1,648 is divisible by 4.

(c) Is 186 divisible by 6? Because 186 ends in 6, it is divisible by 2. Sum of digits = 15. Because 15 is divisible by 3, 186 is divisible by 3. 186 is divisible by 2 and 3; therefore, it is divisible by 6.

(d) Is 2,488 divisible by 8? Because 488 is divisible by 8, then 2,488 is divisible by 8.

(e) Is 2,853 divisible by 9? Sum of digits = 18. Because 18 is divisible by 9, then 2,853 is divisible by 9.

Chapter Check-Out

Q&A

1. Which of the following are integers? 3, 4, , 0, –1, 2

2. Which of the following are prime numbers? 2, 5, 7, 9, 15, 21

3. The identity element in addition is ______.

4. True or false: a(b + c) = (a)(b)(c)

5. 40 =

6. 3– 5 =

7. 45 × 48 = ______ (with exponents)

8. (32)3 = ______ (with exponents)

9. =

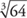10. Approximate: 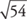(to the nearest tenth)

11. Simplify: 3[10(4 + 32)]

12. The number 6,321 is divisible by which numbers between 1 and 10?

Answers: 1. 3, 4, 0, –1, 2 2. 2, 5, 7 3. 0 4. False 5. 1 6. 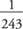7. 413 8. 36 9. 4 10. about 7.3 11. 1080 12. 3, 7