Chapter 12
Quadratic Equations
Chapter Check-In
Solving quadratic equations
The factoring method
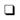The quadratic formula
Completing the square
A quadratic equation is an equation that could be written as ax2 + bx + c = 0 when a ≠ 0.
Solving Quadratic Equations
There are three basic methods for solving quadratic equations: factoring, using the quadratic formula, and completing the square. For a review of factoring, refer to Chapter 6.
Factoring
To solve a quadratic equation by factoring,
1. Put all terms on one side of the equal sign, leaving zero on the other side.
2. Factor.
3. Set each factor equal to zero.
4. Solve each of these equations.
5. Check by inserting your answer in the original equation.
Example 1: Solve x2 – 6x = 16.
Following the steps,
x2 – 6x = 16 becomes x2 – 6x – 16 = 0
Factor.
(x – 8)(x + 2) = 0
Setting each factor to zero,
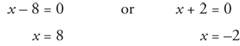
Then to check,
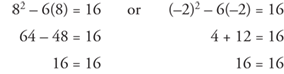
Both values, 8 and –2, are solutions to the original equation.
Example 2: Solve y2 = – 6y – 5.
Setting all terms equal to zero,
y2 + 6y + 5 = 0
Factor.
(y + 5)(y + 1) = 0
Setting each factor to 0,
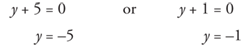
To check, y2 = –6y – 5
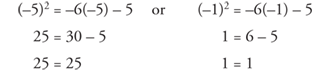
A quadratic with a term missing is called an incomplete quadratic (as long as the ax2 term isn’t missing).
Example 3: Solve x2 – 16 = 0.
Factor.
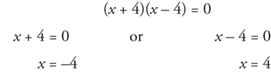
To check, x2 – 16 = 0
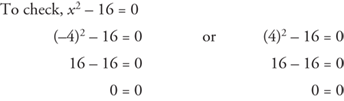
Example 4: Solve x2 + 6x = 0.
Factor.
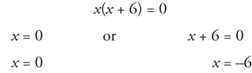
To check, x2 + 6x = 0
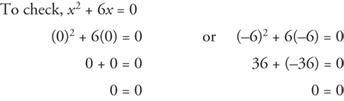
Example 5: Solve 2x2 + 2x – 1 = x2 + 6x – 5.
First, simplify by putting all terms on one side and combining like terms.
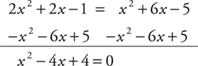
Now, factor.
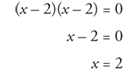
To check, 2x2 + 2x – 1 = x2 + 6x – 5
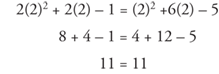
The quadratic formula
Many quadratic equations cannot be solved by factoring. This is generally true when the roots, or answers, are not rational numbers. A second method of solving quadratic equations involves the use of the following formula:
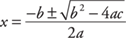
a, b, and c are taken from the quadratic equation written in its general form of
ax2 + bx + c = 0
where a is the numeral that goes in front of x2, b is the numeral that goes in front of x, and c is the numeral with no variable next to it (a.k.a., “the constant”).
When using the quadratic formula, you should be aware of three possibilities. These three possibilities are distinguished by a part of the formula called the discriminant. The discriminant is the value under the radical sign, b2 – 4ac. A quadratic equation with real numbers as coefficients can have the following:
1. Two different real roots if the discriminant b2 – 4ac is a positive number.
2. One real root if the discriminant b2 – 4ac is equal to 0.
3. No real root if the discriminant b2 – 4ac is a negative number.
Example 6: Solve for x: x2 – 5x = –6.
Setting all terms equal to 0,
x2 – 5x + 6 = 0
Then substitute 1 (which is understood to be in front of the x2), –5, and 6 for a, b, and c, respectively, in the quadratic formula and simplify.
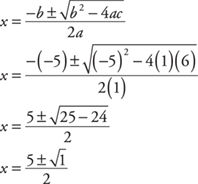
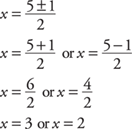
Because the discriminant b2 – 4ac is positive, you get two different real roots.
Example 6 produces rational roots. In Example 7, the quadratic formula is used to solve an equation whose roots are not rational.
Example 7: Solve for y: y2 = –2y + 2.
Setting all terms equal to 0,
y2 + 2y – 2 = 0
Then substitute 1, 2, and –2 for a, b, and c, respectively, in the quadratic formula and simplify.
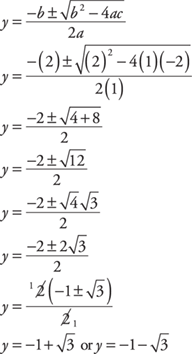
Note that the two roots are irrational.
Example 8: Solve for x: x2 + 2x + 1 = 0.
Substituting in the quadratic formula,
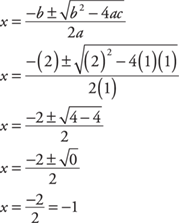
Since the discriminant b2 – 4ac is 0, the equation has one root.
The quadratic formula can also be used to solve quadratic equations whose roots are imaginary numbers, that is, they have no solution in the real number system.
Example 9: Solve for x: x(x + 2) + 2 = 0, or x2 + 2x + 2 = 0.
Substituting in the quadratic formula,
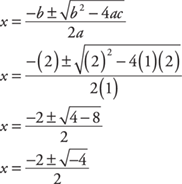
Since the discriminant b2 – 4ac is negative, this equation has no solution in the real number system.
But if you were to express the solution using imaginary numbers, as discussed at the beginning of Chapter 11, the solutions would be
.
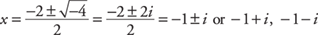Completing the square
A third method of solving quadratic equations that works with both real and imaginary roots is called completing the square.
1. Put the equation into the form ax2 + bx = –c.
2. Make sure that a = 1 (if a ≠ 1, multiply through the equation by 
before proceeding).
3. Using the value of b from this new equation, add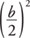 
to both sides
of the equation to form a perfect square on the left side of the equation.
4. Find the square root of both sides of the equation.
5. Solve the resulting equation.
Example 10: Solve for x: x2 – 6x + 5 = 0.
Arrange in the form of
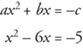
Because a = 1, add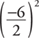 
, or 9, to both sides to complete the square.
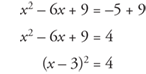
Take the square root of both sides.
x – 3 = ±2
Solve.
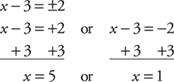
Example 11: Solve for y: y2 + 2y – 4 = 0.
Arrange in the form of
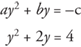
Because a = 1, add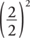 
, or 1, to both sides to complete the square.
or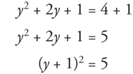 
Take the square root of both sides.
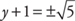
Solve.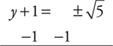 
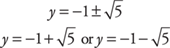
Example 12: Solve for x: 2x2 + 3x + 2 = 0.
Arrange in the form of
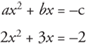
Because a ≠ 1, multiply through the equation by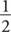 
.
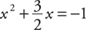
Add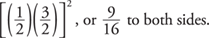 
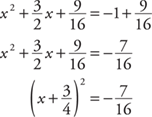
Take the square root of both sides.
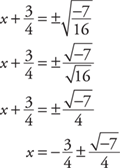
There is no solution in the real number system. It may interest you to know that the completing the square process for solving quadratic equations was used on the equation ax2 + bx + c = 0 to derive the quadratic formula.
Chapter Check-Out
1. Solve for x: x2 + 3x + 2 = 0
2. Solve for x: x2 – 5x = 6
3. Solve for x: x2 = 5x – 4
4. Solve for x: x2 – 49 = 0
5. Solve for x: x2 – 6x = 0
6. Solve for x: 3x2 + 21x = 2x2 – 3x + 81
7. Solve for x by using the quadratic formula: x2 + 5x + 2 = 0
8. Solve for x by completing the square: x2 + 4x + 2 = 0
Answers: 1. –1, –2 2. 6, –1 3. 4, 1 4. 7, –7 5. 0, 6 6. 3, –27
7. 
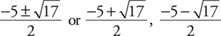8. 