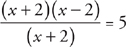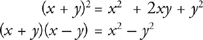Chapter 11
Algebra
Algebra is usually all about writing equations. In this chapter, we’ll show you a fool-proof way to write the equations you need to write, give you a review of the quadratic formula, and teach you how to do simultaneous equations. Plus, you’ll learn two fantastic techniques that will allow you to avoid writing equations on most GMAT questions: Plugging In and Plugging In The Answers (PITA).
NOT EXACTLY ALGEBRA: BASIC PRINCIPLES
Algebra is used to come up with general solutions to problems. For example, you might know (for whatever reason) that the price of a new pair of shoes in relation to the cost of a pair of jeans is 3j + 20, where j is the cost of the jeans. Based on this formula, if you know that the jeans cost $50, then you know that the shoes cost $170. But, you also know the cost of the shoes if the jeans cost $75.
You might consider this question a fairly easy algebra question. To solve it, you might just start translating the phrase “the cost of a pair of shoes is twenty dollars more than three times the cost of a pair of jeans.” But, you need to be careful while doing that. If you get confused about whether you should add 20 or subtract 20, you’ll pick the wrong answer. The test-writers have put a lot of thought into the ways that the key statement in the question can be misinterpreted.
1. Pick numbers for the variables in the problem.
2. Using your numbers, find an answer to the problem. At The Princeton Review, we call this the target answer.
3. Plug your numbers into the answer choices to see which choice equals the answer you found in step 2.

Here’s How to Crack It
Let’s pick a number for j. Let’s say that the jeans cost $10. (We don’t need to worry about being realistic!) In your scratch booklet, write down “j = 10”. We’ve now transformed the problem from an algebra problem into an arithmetic problem.
At a certain store, the price of a pair of shoes is twenty dollars more than three times the price of a pair of jeans. If the price of a pair of jeans is 10 dollars at this store, then what is the price, in dollars, of a pair of shoes, in terms of j ?
You’ll notice that we’ve substituted 10 for the variable j in the original problem. You’ll also notice that we’ve crossed out the phrase “in terms of j”. Once we put a number into the problem, the phrase “in terms of” has no meaning so we can ignore it.
A) 20 – 3j = 20 – 3(10) = –10
B) 3j + 20 = 3(10) + 20 = 50
C) 3j – 20 = 3(10) – 20 = 10
D) 3j + 60 = 3(10) + 60 = 90
E) 20j + 3 = 20(10) + 3 = 203
Answer B is the only answer that matches the target answer so it is the answer to this problem. You’ll note that we checked all five answer choices. We did that to be sure that we were picking the correct answer.

Scratch Work
The students in our GMAT course learn to automatically do scratch work. When plugging in, always write down the numbers you are plugging in for each variable. Be sure to clearly label the number for each variable by writing down something like j = 10. Next, do the work for each step in the problem. When you find the numerical answer to the problem, write that down and circle it. Then, try each of the answer choices, crossing them off as you eliminate them. Here’s what your scratch work should have looked like for the last problem:

Why Plug In? Because It Makes Difficult Problems Easy!
You might be thinking, “Wait a minute! It was just as easy to solve this problem algebraically. Why should I plug in?” To see why, let’s take a look at another version of the problem.

Here’s How to Crack It
This version of the problem is wordier and that helps to make it more confusing. Let’s try plugging in. As before, we’ll start by making j = 10. So, the jeans cost $10. Next, we know the relationship between the price of the jeans and the cost of the shoes. The price of the shoes is “twenty dollars more than three times the price of the jeans.” So, the price of the shoes is $50. Finally, the sweater costs “fifty percent more than the price of the shoes.” So, the sweater is $50 + $25 or $75. So, the cost of all three items is $10 + $50 + $75 = $135. Be sure to circle $135.

To recap, there are two reasons why you’d want to plug in even if you are pretty good at algebra.
- Plugging In can make even the hardest algebra problems much easier to solve.
- The test writers have thought about all the possible ways you might mess up the algebra while working the problem. If you make one of those mistakes, your answer will be among the answer choices and you’ll most likely wind up picking the wrong answer.
What Number Should I Plug In?
While you can plug in any number, you’ll find that certain numbers work better than others. Ideally, you want a number that makes it easy to perform the calculations for the problem. For most problems, you can just use small, simple numbers such as 2, 5, or 10. However, you also want numbers that make sense within the context of the problem. For example, for a problem that uses percents, plugging in 100 would be a good idea. Different numbers work for different types of problems. As you practice, you’ll get better at picking good numbers—especially if you keep asking yourself “What number will make this problem easy?” You also shouldn’t be afraid to change your number if the calculations start to get messy.
Sometimes the best way to select a number is to use a little common sense. Here’s an example:

If Jim drives k miles in 50 minutes, how many minutes will it take him to drive 10 miles, at the same rate?
Here’s How to Crack It
GMAC would like you to use the formula distance = rate × time. There are variables in the answer choices, so we can plug in. Since it’s a good bet that at least a few of the wrong answers are based on using the formula, let’s plug in.
If Jim drives 5 miles in 50 minutes, how many minutes will it take him to drive 10 miles, at the same rate?

More Times to Plug In
So far, we’ve been looking at questions that have explicit variables in both the problem and the answer choices. When you see variables in the problem or answer choices, that’s one of the signs to plug in.
Plugging In with Hidden Variables
Some problems have a hidden variable. For these problems, all the calculations are usually based off one item but you don’t know the value of that item. There’s a simple solution—just plug in a value for the item!

A merchant reduces the original price of a coat by 20 percent
for a spring sale. Finding that the coat did not sell, the merchant reduces the spring price by a further 15 percent at the start of the summer. The coat’s summer price is what percent of its original price?
Here’s How to Crack It
You may have noticed that this problem never gave us the coat’s original price. You may have felt the urge to do algebra starting to kick in as you read the problem. For example, you might have started to say to yourself “Well, if the price of the coat is x, then the spring price is …” That’s your sign that you can do this problem as a Plug In! All you need to do is pick a price for the coat.
If you were running out of time, you’d need to make a guess. But, you could eliminate some obviously wrong answers first. When you read the problem fast, you might be tempted to think that the overall reduction is 20% + 15% = 35% but that’s too easy. So, cross off choice A. Choice C is just 100 − 35 = 65. Also, too easy. Finally, choice E is what you get after the first reduction. The answer is probably B or D.


Another way to tell that you can probably solve a question as a hidden plug in is to look at the answer choices. The answer choices for hidden plug in questions are typically percents, fractions, or sometimes ratios. How can you tell that this problem is a hidden plug in?

At College P, one–fourth of the students are seniors and one–fifth of the seniors major in business. If two–fifths of all students at the college major in business, the business majors who are not seniors are what fraction of all business majors?
Here’s How to Crack It
You may have noticed that while this problem provides lots of fractions to work with, it never reveals how many students attend College P. Of course, knowing the total enrollment at the college would make solving the problem fairly straightforward. So, before you start setting up equations based on x students at College P, let’s plug in a number for the total students.
So, if there are 100 students at the college, there are 25 seniors and 75 students who are not seniors. Next, you know that one-fifth of the seniors major in business, so that’s 5 seniors who are business majors. Since two-fifths of all students are business majors, the college has 40 business majors. Of those 40 business majors, 40 − 5 = 35 of the business majors are not seniors. So, the fraction of business majors who are not seniors is  . The correct answer is E.
. The correct answer is E.

Plugging In the Answers (PITA)
Some algebra questions ask for a numerical answer. GMAC expects you to write an equation, solve it and then pick the answer. However, the person who wrote the problem had to do all of that hard work. So, rather than duplicate all of the work the question writer did, why not just test out the answers to see which one works?
- Write down the answers, determine what they represent and label them.
- Start with choice C and work the steps of the problem.
- Look for some sort of condition that must be met to make the answer correct.
Let’s take a look at an example.

Here’s How to Crack It
If there were no answer choices, you’d be forced to write an equation and solve it. However, because you know the answer must be one of the five provided choices, it will be easier and faster to simply try the answers.
So far, your work should look like this:

Now, its time to decide if you need a bigger number or a smaller numbers. It’s a pretty easy choice for this problem. Since $4.00 turned out to be too big, it makes sense to try a smaller number. There’s no need to debate over choice A or B. One of them must be correct, so just try choice B. If it works, you’re done. If it doesn’t, choose choice A and you’re still done.


Plugging In the Answers: Advanced Principles
When you solve a problem using Plugging In the Answers (PITA), you’ll usually know if you need a bigger or smaller number if choice C didn’t work. However, there are times that you won’t be sure. Rather than wasting time trying to decide if you need a bigger or smaller number, just pick a new number and try it. You’ll actually waste less time testing an extra answer choice or two than you will trying to decide which type of number to try next.

Jim is now twice as old as Fred, who is and two years older than Sam. Four years ago, Jim was four times as old as Sam. How old is Jim now?
Here’s How to Crack It
This question has numbers in the answers and you probably started to think “Well, if Jim is x years old, then Fred is …” The urge to do algebra means that it’s time to plug in the answers. Start with choice C.
In this case, Jim’s age four years ago must be four times that of Sam. Is 12 four times 2? No. So, choice C can be eliminated.

Now, it’s time to choose a bigger or smaller number. But, it isn’t really clear which direction to go, is it? So, rather than waste a lot of time trying to figure that out, just pick an answer and try it. If Jim is 20 years old now (choice D), then Fred is 10 and Sam is 8. Four years ago, Jim was 16 and Sam was 4.

Since 4 × 4 = 16, the condition in the problem is met. Choice D is the correct answer.

Most of the time, starting at C when doing PITA makes the most sense. By starting at C, you can usually cut down on the number of answer choices that you need to test. However, there can be times when it makes sense to start with a different answer choice.

If x is a positive integer such that x2 + 5x − 14 = 0, what is the value of x ?
Here’s How to Crack It
Notice that the question states that x is a positive integer. Don’t waste time with choices A, B, or C—cross them off immediately. For this problem, it makes sense to start with choice D. Plug 2 into the equation for x to get (2)2 + 5(2) − 14 = 0. Since the equation is true when x = 2, choice D is the correct answer.

- If you’re not sure whether you need a bigger or smaller number, don’t waste time. Just pick a new number and try it.
- You may be able to eliminate some numbers that are too big or too small before you start plugging in. If you can, just start with the middle number that you have left.
- If you have both easy to work with numbers and messy numbers in the answer choices, try the easy to work with numbers first.
Must Be
Some questions will use the words “must be.” For example, the question may ask which of the expressions in the answers must be even or must be divisible by 3. These questions can be solved easily by plugging in. However, you’ll probably need to plug in at least twice to find the answer.
- Pick numbers for the variables in the problem. Be sure to satisfy any restrictions for the variables.
- Eliminate any answer choices that don’t match what you are looking for.
- Plug in the most different kind of number you are allowed to try. For example, if you tried an even number, try an odd number.
- Repeat until only one answer remains.

Here’s How to Crack It
Start by picking a value for n. How about n = 2? Now, evaluate each answer choice. For choice A, the expression equals 3, so cross it off. For choice B, the expression equals 0. Remember that 0 is an even number so keep this answer choice. Keep checking the answers. Choice C is also equal to 0, so keep it as well. Choice D equals −3. Don’t be fooled by the negative sign. Negative integers can also be even or odd. Since −3 is odd, cross this answer off. Choice E equals −7 and can also be eliminated.


BASIC ALGEBRA
You can solve most GMAT algebra problems using some form of Plugging In. However, there are some questions that you may need to solve using some relatively basic algebra.
Two Simple Rules
Before we review some very specific types of algebra that GMAC likes to test, let’s review the two basic rules that are true for any algebraic situation. These two rules are used pretty much any time that you solve a problem algebraically.
- Collect like terms. Get all the x’s on one side of the equal sign and all the numbers on the other.
- Whatever you do to one side of an equation, you need to do to the other side of the equation. Did you multiply one side by 5? Then, you need to multiply the other side of the equation by 5, as well.
Solving Equalities
Even the simplest equalities can be solved by Plugging In the Answers, but it’s probably easier to solve a simple equation algebraically. If there is one variable in an equation, isolate the variable on one side of the equation and solve it. Let’s try an example of this type, although a question this easy wouldn’t actually be seen on the GMAT. This one is just for practice.

If x – 5 = 3x + 2, then x =
Here’s How to Crack It
Get all of the x’s on one side of the equation. If we subtract x from both sides we have:

Now subtract 2 from both sides:

Finally, divide both sides by 2:

The answer is choice B.

Solving Inequalities
To solve inequalities, you must be able to recognize the following symbols:
| > |
is greater than |
| < |
is less than |
| ≥ |
is greater than or equal to |
| ≤ |
is less than or equal to |
As with an equation, you can add a number to or subtract a number from both sides of an inequality without changing it; you can collect similar terms and simplify them. In fact, an inequality behaves just like a regular equation except in one way:
If you multiply or divide both sides of an inequality by a negative number, the direction of the inequality symbol changes.
For example,
–2x > 5

Solving Simultaneous Equations
Simultaneous equations are almost always tested in data sufficiency format on the GMAT. It’s impossible to solve one equation with two variables. But if there are two equations, both of which have the same two variables, then it is possible to solve for both variables. An easy problem might look like this:
If 3x + 2y = 6 and 5x – 2y = 10, then x = ?
To solve simultaneous equations, add or subtract the equations so that one of the variables disappears.

In more difficult simultaneous equations, you’ll find that neither of the variables will disappear when you try to add or subtract the two equations. In such cases you must multiply both sides of one of the equations by some number in order to get the coefficient in front of the variable that you want to disappear to be the same in both equations. This sounds more complicated than it is. A difficult problem might look like this:
If 3x + 2y = 6 and 5x – y = 10, then x = ?
Let’s set it up the same way:
Unfortunately, in this example, neither adding nor subtracting the two equations gets rid of either variable. But look what happens when we multiply the bottom equation by 2:
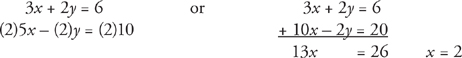
Quadratic Equations
On the GMAT, quadratic equations always come in one of two forms: factored or expanded. Here’s an example:
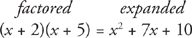
The first thing to do when solving a problem that involves a quadratic equation is to see which form the equation is in. If the quadratic equation is in an unfactored form, factor it immediately. If the quadratic equation is in a factored form, unfactor it. The test writers like to see whether you know how to do these things.
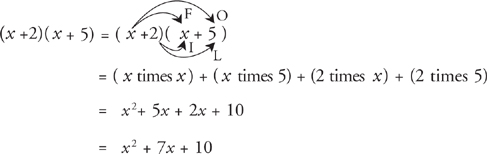
To factor an unfactored expression, put it into the following format and start by looking for the factors of the first and last terms.
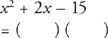
For the first term of the unfactored expression to be x2, the first term of each parentheses of the factored expression has to be x.

For the last term of the unfactored expression to be 15, the last term in each parentheses of the factored expression must be either 5 and 3 or 15 and 1. Since there is no way to get a middle term for the unfactored expression with a coefficient of 2 if the terms were 15 and 1, we are left with

To decide where to put the pluses and minuses in the factored expression, look to see how the inner and outer terms of the factored equation would combine to form the middle term. If we put a minus in front of the 5 and a plus in front of the 3, then the middle term would be –2x (not what we wanted). Therefore, the final factored expression looks like this

Quadratic equations are usually set equal to 0. Here’s an example:

Here’s How to Crack It
This problem contains an unfactored equation, so let’s factor it.

In order for this equation to be correct, x must be either –3 or –1. The correct answer is choice C.

Favorites of GMAT Test Writers
There are three types of quadratic equations the GMAT test writers find endlessly fascinating. These equations appear on the GMAT with great regularity in both the problem-solving format and the data-sufficiency format:
(x + y)2 = x2 + 2xy + y2
(x + y)(x – y) = x2 – y2
(x – y)2 = x2 – 2xy + y2
Memorize all three of these. As with all quadratic equations, if you see the equation in factored form, you should immediately unfactor it; if it’s unfactored, factor it immediately. Here’s an example:

If 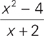 , then x =
, then x =
Here’s How to Crack It
It is unfactored, so let’s factor it:
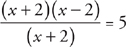
The (x + 2)s cancel out, leaving us with (x – 2) = 5. So x = 7, and the answer is choice D.

Summary
- Most of the algebra problems on the GMAT are simpler to solve without algebra, using two Princeton Review techniques: Plugging In and Plugging In The Answers.
- Plugging In is easy. There are three steps:
- Pick numbers for the variables in the problem. (Write them down in your scratch booklet.)
- Using your numbers, find an answer to the problem. (Write that answer down and circle it.)
- Plug your numbers into the answer choices to see which choice equals the answer you found in the previous step.
- When you plug in, try to choose convenient numbers—those that are simple to work with and make the problem easier to manipulate.
- When you plug in, avoid choosing 0, 1, or a number that already appears in the problem or in the answer choices.
- On problems with variables in the answers that contain the words “must be” or “could be,” you may have to plug in more than once to find the correct answer.
- Plugging In The Answers is easy. There are three steps:
- Always start with answer choice C. Plug that number into the problem and see whether it makes the problem work.
- If choice C is too small, try the next larger number.
- If choice C is too big, try the next smaller number.
- If you’re not sure which way to go, don’t sweat it. Just pick a direction and try it out!
- If you see a problem with a quadratic equation in factored form, the easiest way to get the answer is to expand the equation immediately. If the equation is expanded, factor it immediately.
- Memorize the factored and expanded forms of the two most common quadratic equations on the GMAT:
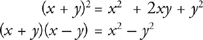
- On problems containing inequalities, remember that when you multiply or divide both sides of an inequality by a negative number, the sign flips.
- In solving simultaneous equations, add or subtract one equation to or from another so that one of the two variables disappears.






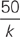



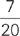



 . The correct answer is E.
. The correct answer is E.












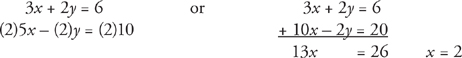
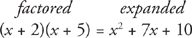
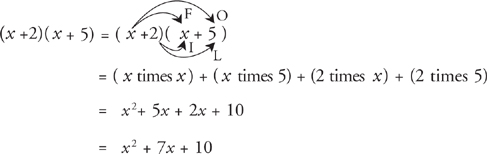
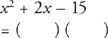




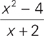 , then x =
, then x =