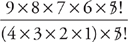Chapter 12
Applied Arithmetic
Applied arithmetic involves knowing how to solve word problems involving rate and work, functions, probability, permutations, and combinations. In this chapter, we cover the important facets of each type of problem and show you how they appear on the GMAT.
- Rate problems
- Work problems
- Function problems
- Probability problems
- Permutation and Combination problems
RATE PROBLEMS
Any problem that mentions planes, trains, cars, bicycles, distance, miles per hour, or any other travel-related terminology is asking you to solve a rate problem. You may remember that you can use the formula distance = rate × time to solve these types of problems.

If a problem gives you the rate and time, the pieces on the bottom, you multiply to get the distance. If you have the distance, the piece on the top, and one of the pieces on the bottom, you divide to get the other bottom piece. As soon as you know that you are dealing with a rate problem, draw a rate pie and start filling in what you know.

Pam and Sue drove in the same car to a business meeting that was 120 miles away. Pam drove to the meeting at 60 miles per hour and Sue drove back, along the same route, at 50 miles per hour. How many more minutes did it take Sue to drive the distance than it took Pam?
Here’s How to Crack It
Since the problem deals with rates, you need a rate pie. In fact, since there is rate information for both Pam and Sue, you need two rate pies—one for Pam and one for Sue.

Once you draw the pies, you can transfer the information that you know to each pie. Since Pam and Sue drove along the same route, the distance is 120 miles for each pie. Pam’s rate is 60 miles per hour and Sue’s rate is 50 miles per hour. Transfer that information to the pies, too.
The problem asks how many more minutes it took Sue to drive the distance than it took Pam. Start by subtracting 2 – 2 =
– 2 =  to find that it took Sue
to find that it took Sue  of an hour longer. Now, just convert to minutes: 60 ×
of an hour longer. Now, just convert to minutes: 60 ×  = 24. The answer is choice D.
= 24. The answer is choice D.

Now, let’s look at a slightly harder problem:

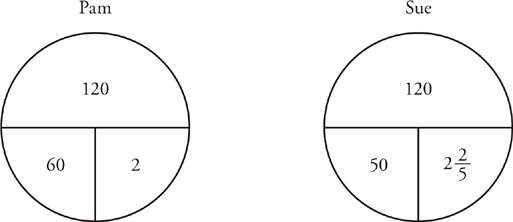
Fred and Sam are standing 45 miles apart and they start walking in a straight line toward each other at the same time. If Fred walks at a constant speed of 4 miles per hour and Sam walks at a constant speed of 5 miles per hour, how many miles has Sam walked when they meet?
Here’s How to Crack It
Since the problem is about rates, draw a rate pie. In this case, you may be wondering if you need one pie or two. You actually need one. Here’s why: When dealing with rates, it is often helpful to think about what happens in a certain amount of time like an hour. In one hour, Fred walks 4 miles and Sam walks 5 miles. Since they are walking toward each other in a straight line, they have covered 9 miles of the distance between them at the end of an hour. Wait! Nine miles in an hour? That means that their combined rate is 9 miles per hour. That’s what goes on the pie for the rate.
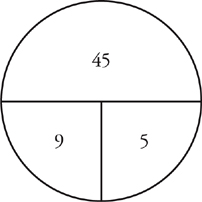
The other piece that you could fill in on the pie from the problem was the distance, 45 miles. Then, use the pie to find that Fred and Sam walk for 5 hours before they meet. (Remember that you divide the top piece of the pie by one of the pieces on the bottom to find the other bottom piece.)
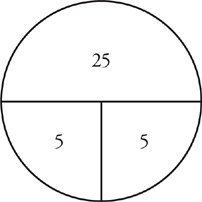
So, Sam walks 25 miles when he meets Fred. The answer is choice C.

WORK PROBLEMS
Work problems are a type of rate problem. Rather than asking about a distance, these problems ask about a job or a part of a job. You can use a variation of the rate pie to solve these problems. Here’s what it looks like:

All that changes is that work replaces distance at the top of the pie. You use the work pie in the same way as the rate pie.

Working at a constant rate, Sam can finish a job in 3 hours. Mark, also working at a constant rate, can finish the same job in 12 hours. How many hours does it take Mark and Sam to finish the job if they work together each at his respective, constant rate?
Since the problem mentions a job being completed, you can use a work pie. You’ll actually need two pies for the first step of the problem since you’ll want to find each worker’s individual rate. Once you draw your pies, you can put each worker’s time on the pie. You can also put 1 for the work since they each complete 1 job.
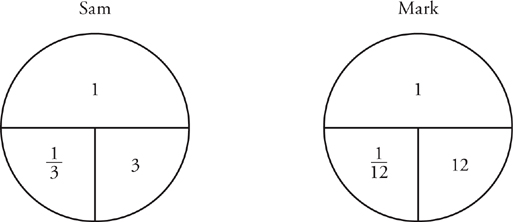
So, Sam’s rate is  and Mark’s rate is
and Mark’s rate is  . What does that mean? Well, it means that Sam completes
. What does that mean? Well, it means that Sam completes  of the job every hour while Mark completes
of the job every hour while Mark completes  of the job every hour.
of the job every hour.

Divide the amount of work by the combined rate to find that the time to complete the job is  hours. The correct answer is B.
hours. The correct answer is B.

Same Problem, Different Approach
Another way to look at this problem is to realize that the actual job is never specified. But, wouldn’t the problem be much easier to solve if you knew how many of something Sam and Mark needed to make? In other words, this problem can be approached as a Plug In.
Again, it takes them  hours to complete the job. The answer is choice B.
hours to complete the job. The answer is choice B.
It stands to reason that two men working together would take less time to finish a job than they would if each of them worked alone. Because Sam, working alone, could finish the job in 3 hours, it must be true that the two of them, working together, could do it in less time. The answer to this question has to be less than 3. Therefore we can eliminate answer choices D and E.

Here’s a slightly harder version of the problem above:

Working at a constant rate, Sam can finish a job in 3 hours. Mark, also working at a constant rate, can finish the same job in 12 hours. If they work together for 2 hours, how many minutes will it take Sam to finish the job, working alone at his constant rate?
Here’s How to Crack It
This problem starts in the same way so you can use the same work pies to find each worker’s rate.
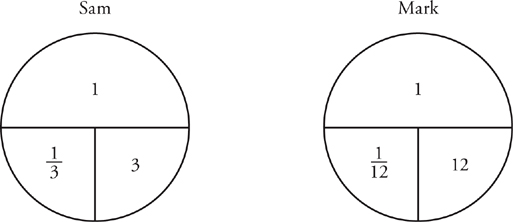
Now, you need a new pie. For this pie, you know the combined rate, 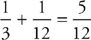 , and that they work together for two hours.
, and that they work together for two hours.
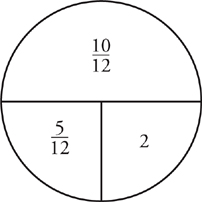
So, you now know that  of the job has been completed when Mark goes home. Sam must finish
of the job has been completed when Mark goes home. Sam must finish  of the job on his own. Of course, you know Sam’s rate, so just set up one last work pie.
of the job on his own. Of course, you know Sam’s rate, so just set up one last work pie.

To find the time for Sam to finish the job, use the pie to find that 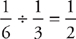 or 30 minutes. The correct answer is C.
or 30 minutes. The correct answer is C.

Functions
You know you’ve hit a function problem by the sensation of panic and fear you get when you see some strange symbol ($ or # or * or ∆) and say, “I studied for two months for this test and somehow managed to miss the part where they told me about # or * or ∆.” Relax. Any strange-looking symbol on the GMAT is just a function, and on this test, functions are easy.
A function is basically a set of directions. Let’s look at an example:

If ∆ x = x for x ≥ 0 and 2x for x < 0, 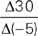 =
=
Here’s How to Crack It
A function is basically a set of directions. In this case, the directions tell you what to do with the number that comes after the symbol Δ. If the number that follows the symbol is greater than or equal to 0, then the output of the function is just the number x. However, if the number that follows the symbol is negative, the output of the Δ function is 2x. So, we can evaluate the given expression thus:
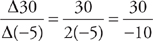
or –3. The answer is choice C.
Joe has no idea what to do with ∆, so he just ignores it. Because 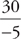 , Joe picks answer choice B. On the other hand, Joe might also think he can reduce functions. In other words, he might think he could do this:
, Joe picks answer choice B. On the other hand, Joe might also think he can reduce functions. In other words, he might think he could do this:
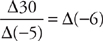
The function of –6 = –12, so Joe might also select answer choice A.


You may remember seeing a different notation for functions in school. The standard math notation for functions is f(x)—pronounced f of x—and the GMAT test writers will sometimes ask function questions using this notation, too.

Here’s How to Crack It
Plug in a value for x and use that value to see if f(x) = f(−x) for each of the functions in the answer choices. So, for example, look at answer A if x = 2. Does
(2)3 + 3 = (−2)3 + 3? No, so eliminate answer A.

PROBABILITY
Probability, Part 1
Just the word is enough to cause math-phobes to run for the exits—but, at least as it appears on the GMAT, probability really isn’t all that bad. Check out the easy example below:
A six-sided die, with faces numbered one through six is rolled once. What is the probability that the face numbered 2 is facing upward?
Well, of course, there’s only one possibility of this happening, and there are six possible outcomes, so there’s a one-in-six chance. In essence, this is all that probability is about. On the GMAT, probability is usually expressed as a fraction: The total number of possibilities is always the denominator. The number of possibilities that match what you want is the numerator. In the example above, that translates to  .
.
Let’s make this example a little harder:
A six-sided die with faces numbered one through six is rolled once. What is the probability that either the face numbered two or the face numbered three is facing up?
The total number of possible outcomes (the denominator) is still the same: 6. But the numerator is different now. There are two possibilities that would match what we want, so the numerator becomes 2. The probability is  , or
, or  .
.
A six-sided die with faces numbered one through six is rolled twice. What is the probability that the face numbered 2 is facing up after both rolls?
Obviously, the odds of this happening are much smaller. How do you figure out the probability of something happening over a series of events? It’s actually pretty easy. To find the probability of a series of events, you multiply the probabilities of each of the individual events. Let’s start with the first roll of the die. We already figured out that the probability of the die landing with its “2” side facing up on a single toss is  . Now, let’s think about the second toss. Well, actually, the probability of this happening on the second toss is exactly the same:
. Now, let’s think about the second toss. Well, actually, the probability of this happening on the second toss is exactly the same:  .
.
The probability that A and B will both happen: A × B
Here’s an example of a moderately difficult GMAT problem.

There are 8 job applicants sitting in a waiting room—4 women and 4 men. If 2 of the applicants are selected at random, what is the probability that both will be women?
Here’s How to Crack It
Let’s take the first event in the series. The total number of possibilities for the first selection is 8, because there are 8 applicants in the room. Of those 8 people, 4 are women, so the probability that the first person chosen will be a woman is  , or
, or  . You might think that the probability would be exactly the same for the second choice (in which case you would multiply
. You might think that the probability would be exactly the same for the second choice (in which case you would multiply  ×
×  and choose answer choice C), but in fact, that’s not true. Let’s consider: The first woman has just left the room, and they are about to choose another applicant at random. How many total people are now in the room? Aha! Only 7. And how many of those 7 are women? Only 3. So the probability that the second choice will be a woman is actually only
and choose answer choice C), but in fact, that’s not true. Let’s consider: The first woman has just left the room, and they are about to choose another applicant at random. How many total people are now in the room? Aha! Only 7. And how many of those 7 are women? Only 3. So the probability that the second choice will be a woman is actually only  , which is choice B. But we aren’t done yet. We have to figure out the probability that BOTH choices in this series of two choices will be women. The probability that the first will be a woman is
, which is choice B. But we aren’t done yet. We have to figure out the probability that BOTH choices in this series of two choices will be women. The probability that the first will be a woman is  . The probability that the second will be a woman is
. The probability that the second will be a woman is  . The probability that they both will be women is
. The probability that they both will be women is  ×
×  , or
, or  . The answer is choice D.
. The answer is choice D.
The GMAT test writers like to see if they can trick you into picking partial answers—i.e., numbers that you get in the course of solving a problem that are not quite the final answer. The probability that the first choice will be a woman is  , choice A—but does it feel like you’ve done enough work to “deserve” to get this problem right yet? Nope—this is only an intermediate step. The probability that the second choice will be a woman is
, choice A—but does it feel like you’ve done enough work to “deserve” to get this problem right yet? Nope—this is only an intermediate step. The probability that the second choice will be a woman is  , choice B. But again, this is just another intermediate step. Don’t fall for these trick choices—cross off choices A and B.
, choice B. But again, this is just another intermediate step. Don’t fall for these trick choices—cross off choices A and B.


Probability, Part 2: One Thing or Another
So far, we’ve been dealing with the probability of one event happening and then another event happening (for example, in that last problem, the first event was choosing a female job applicant; the second event was choosing ANOTHER female job applicant). But what if you are asked to find the probability of either one thing OR another thing happening? To solve this type of problem, you simply add the probabilities. Note that pure versions of these ‘or’ problems are incredibly rare on the GMAT. Understanding the idea can be helpful on other problems, however.
The probability that A or B will happen: A + B
Here’s an example:

Sally and Sam are watching a magician perform with 16 of their friends. If the magician chooses one child at random to assist with a trick, what is the probability that either Sally or Sam is chosen?
Here’s How to Crack It
By this point, you should have no problem figuring out that the probability of Sally being chosen is  . And the probability of Sam being chosen? That’s right:
. And the probability of Sam being chosen? That’s right:  . So what is the probability of Sally or Sam being chosen?
. So what is the probability of Sally or Sam being chosen?


Probability, Part 3:
The Odds That Something Doesn’t Happen
But what if you are asked to find the probability that something will NOT happen? Well, think of it this way: If the probability of snow is 70% or 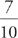 , what’s the probability that it won’t snow? That’s right: 30% or
, what’s the probability that it won’t snow? That’s right: 30% or 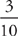 . To figure out the probability that something won’t happen, simply figure out the probability that it WILL happen, and then subtract that fraction from 1.
. To figure out the probability that something won’t happen, simply figure out the probability that it WILL happen, and then subtract that fraction from 1.
Here’s an example:

Sally and Sam are watching a magician perform with 16 of their friends. If one child is chosen at random to assist with a trick, what is the probability that neither Sally nor Sam is chosen?
Here’s How to Crack It
As we already know, the probability that Sally will be chosen is  . The probability that Sam will be chosen is also
. The probability that Sam will be chosen is also  . So what is the probability that neither Sally nor Sam will be chosen?
. So what is the probability that neither Sally nor Sam will be chosen?


Probability, Part 4:
The Odds That at Least One Thing Will Happen
What if the problem asks the probability of something happening at least once? To calculate the probability of at least one thing happening, just use this equation: The probability of what you WANT to happen plus the probability of what you DON’T want to happen equals one.
Here’s an example:

Nine boys and nine girls are watching a magician perform. Four times during the performance a child is chosen at random to assist with a trick. If any of the children can be chosen to assist with each of the four tricks, what is the probability that at least one girl is chosen?
Here’s How to Crack It
To find out the odds of at least one girl being chosen, let’s begin by figuring out the odds that a girl isn’t chosen. The magician will make a total of four choices. What are the odds that the magician will not pick a girl in the first round? If you said  or
or  , you are doing just fine. And what are the odds that the magician will not pick a girl the second, third, and fourth round? Each time, the odds of not picking a girl stay the same, because the children are returned to the pool of possible candidates, so each time the odds will be
, you are doing just fine. And what are the odds that the magician will not pick a girl the second, third, and fourth round? Each time, the odds of not picking a girl stay the same, because the children are returned to the pool of possible candidates, so each time the odds will be  or
or  . The probability of not picking a girl all four times is:
. The probability of not picking a girl all four times is:
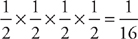
But we aren’t done. The probability of a girl being picked at least once is
1 minus the probability that she will not be picked. So the correct answer is:
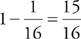

PERMUTATIONS AND COMBINATIONS
In general, permutation and combination problems tend to show up as medium-hard to hard problems on the GMAT.

At a restaurant, you must choose an appetizer, a main course, and a dessert. If there are 2 possible appetizers, 3 possible main courses, and 5 possible desserts, how many different meals could you order?
Here’s How to Crack It
You could just carefully write down all the different combinations:
Shrimp cocktail with meatloaf with ice cream
Shrimp cocktail with meatloaf with…
For a problem that asks you to choose a number of items to fill specific spots, when each spot is filled from a different source, all you have to do is multiply the number of choices for each of the spots.
So, because there were 2 appetizers, 3 main courses, and 5 possible desserts, the total number of combinations of a full meal at this restaurant would be 2 × 3 × 5, or 30. The answer is choice B.

Permutations: Single Source, Order Matters
The same principle applies when you’re choosing from a group of similar items—with one slight wrinkle. Take a look at this easy permutation problem:

Three basketball teams play in a league against each other. At the end of the season, how many different ways could the 3 teams end up ranked against each other?
Here’s How to Crack It
You could just carefully write down all the different combinations. If we call the three teams A, B, and C, then here are the different ways they could end up in the standings:
ABC ACB BAC BCA CAB CBA
But again, this approach is time-consuming (even more so for more difficult problems). As you probably suspected, there’s a simpler and faster way to solve this problem.
For a problem that asks you to choose from the same source to fill specific spots, all you have to do is multiply the number of choices for each of the spots—but the number of choices keeps getting smaller.
Let’s think for a moment about how many teams could possibly end up in first place. If you said 3, you’re doing just fine.
To find the number of different ways these teams could end up in the rankings, just multiply the number of choices for first place (in this case, 3) times the number of choices for second place (in this case, 2) times the number of choices for third place (in this case, 1).
3 × 2 × 1 = 6
The correct answer is choice C.

In general, no matter how many items there are to arrange, you can figure out the number of permutations of a group of n similar objects with the formula:
n(n – 1)(n – 2) … × 3 × 2 × 1, or n!
So if there were 9 baseball teams, the total number of permutations of their standings would be 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1, also sometimes written as 9! If 4 sailboats sailed a race, the total number of permutations of the orders in which they could cross the finish line would be 4 × 3 × 2 × 1, also sometimes written as 4!
Single Source, Order Matters but Only for a Selection
The problems we’ve shown you so far were necessary to show you the concepts behind permutation problems—but were much too easy to be on the GMAT. Here’s a problem that would be more likely to appear on the test:

Seven basketball teams play in a league against each other. At the end of the season, how many different arrangements are there for the top 3 teams in the rankings?
If you were to see this problem on the computer-adaptive section of the actual GMAT, you should first stop and give yourself a pat on the back, because it means you’re doing pretty well—permutation and combination problems usually only show up only among the more difficult problems. But after you’ve congratulated yourself, stop and think for a moment. Could the answer to this difficult problem simply be a matter of finding 7 × 6 × 5 × 4 × 3 × 2 × 1, choice D? Too easy. Because the question is asking for the permutations for only 3 of the 7 slots, the number must be less than that. So get rid of choices D and E.
Here’s How to Crack It
To find all the possible permutations of the top 3 out of 7 baseball teams, simply multiply the number of combinations for each spot in the standings. How many teams are possibilities for the first place slot? If you said 7, you’re right. How about for the second slot? Well, one team is already occupying the first place slot, so there are only 6 contenders left. And for the third place slot? That’s right: 5.

In general, no matter how many items there are to arrange, you can figure
out the number of permutations of r objects chosen from a set of n objects with the formula:
n(n – 1)(n – 2) … × (n – r + 1)
So if there were 9 baseball teams (n), the total number of permutations of the top 4 teams (r) would be 9 × 8 × 7 × 6. If 4 sailboats sailed a race (n), the total number of permutations of the first 3 boats to cross the finish line (r) would be 4 × 3 × 2. Here is another way to write this same formula:

(where n = total items and r = the number selected)
Combinations: Single Source, Order Doesn’t Matter
In the previous problems, the order in which the items are arranged actually matters to the problem. For example, if the order in which the three teams finish a season is Yankees, Red Sox, Orioles—that’s entirely different than if the order were Red Sox, Yankees, Orioles, especially if you’re from Boston.
But combination problems don’t care about the order of the items.

Six horses are running in a race. How many different groups of horses could make up the first 3 finishers?
If we cared about the order in which the top 3 horses finished the race, then the answer would be the number of permutations: 6 × 5 × 4, or 120. But in this case, we only care about the number of unique permutations, and that means the number will be smaller because we don’t have to count the set of, for example, (Secretariat, Seattle Slew, and Affirmed) and the set of (Seattle Slew, Secretariat, and Affirmed) as two different permutations. If the correct answer must be smaller than 120, then we can eliminate choices D and E—they’re too big.
Here’s How to Crack It
To find the number of combinations, first find the number of permutations. If 6 horses run in the race, and we are interested in the top 3 finishers, then the number of permutations would be 6 × 5 × 4, or 120. But if we don’t care about the order in which they finished, then a bunch of these 120 permutations turn out to be duplicates.

In general, no matter how many items there are to arrange, you can figure out the number of combinations of r objects chosen from a set of n objects with
the formula:

So if there were 9 baseball teams, the total number of combinations of the top 4 teams would be:
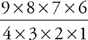
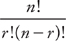
because  is the same as
is the same as 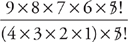
Summary
- Rate problems and work problems can be solved using your handy rate or work pies.
- The key to work problems is to think about how much of the job can be done in one hour. But remember, it is often easier to simply plug in.
- A function problem may have strange symbols like $, ∆, or *, but it is really just a set of directions.
- Probability problems can be solved by putting the total number of possibilities in the denominator, and the number of possibilities that match what you are looking for in the numerator.
- Permutation and combination problems ask you to choose or arrange a group of objects.




 . The pies made it easy to see how to find the time for each driver.
. The pies made it easy to see how to find the time for each driver.





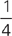

 and Mark’s rate is
and Mark’s rate is  . What does that mean? Well, it means that Sam completes
. What does that mean? Well, it means that Sam completes  of the job every hour. When people work together, you can combine their rates. Now, set up one more work pie. Use 1 for the amount of work and for the rate.
of the job every hour. When people work together, you can combine their rates. Now, set up one more work pie. Use 1 for the amount of work and for the rate.
 hours. The correct answer is B.
hours. The correct answer is B.
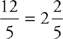 hours to complete the job. The answer is choice B.
hours to complete the job. The answer is choice B.

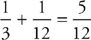 , and that they work together for two hours.
, and that they work together for two hours.
 of the job has been completed when Mark goes home. Sam must finish
of the job has been completed when Mark goes home. Sam must finish  of the job on his own. Of course, you know Sam’s rate, so just set up one last work pie.
of the job on his own. Of course, you know Sam’s rate, so just set up one last work pie.
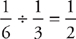 or 30 minutes. The correct answer is C.
or 30 minutes. The correct answer is C.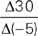 =
=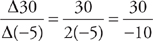 or –3. The answer is choice C.
or –3. The answer is choice C.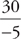 , Joe picks answer choice B. On the other hand, Joe might also think he can reduce functions. In other words, he might think he could do this:
, Joe picks answer choice B. On the other hand, Joe might also think he can reduce functions. In other words, he might think he could do this: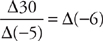

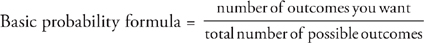
 , or
, or  ×
×  .
.



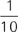
 , or
, or  . You might think that the probability would be exactly the same for the second choice (in which case you would multiply
. You might think that the probability would be exactly the same for the second choice (in which case you would multiply  . The answer is choice D.
. The answer is choice D.
 . And the probability of Sam being chosen? That’s right:
. And the probability of Sam being chosen? That’s right: 
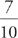 , what’s the probability that it won’t snow? That’s right: 30% or
, what’s the probability that it won’t snow? That’s right: 30% or 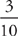 . To figure out the probability that something won’t happen, simply figure out the probability that it WILL happen, and then subtract that fraction from 1.
. To figure out the probability that something won’t happen, simply figure out the probability that it WILL happen, and then subtract that fraction from 1.
 or
or 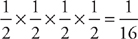
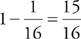





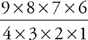
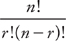
 is the same as
is the same as