Chapter 26
GMAT Math and Verbal Practice Bins: Answers and Explanations
If you really want to improve your score, then you should read all the explanations for all the questions on the pages that follow, not just the ones you got wrong. It’s important to make sure you’re getting questions correct for the right reasons and even more important that you are recognizing opportunities to use The Princeton Review techniques, which can save you time and eliminate the possibility of careless errors.
MATH BIN 1
EXPLANATIONS
1. C Since this is a percent problem, you can solve it by thinking in terms of 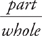 . In this case,
. In this case, 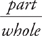 =
= 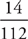 =
=  ; cross-multiply to get 112x = 1,400, so x =
; cross-multiply to get 112x = 1,400, so x =  , and x = 12.5.
, and x = 12.5.
Like most percent questions on the GMAT, you can also find the answer using POE. 14 is a little bigger than 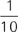 , or 10%, of 112—11.2 is exactly 10%—so the answer can only be C.
, or 10%, of 112—11.2 is exactly 10%—so the answer can only be C.
2. C Rather than try to rely on high school-style exponential growth formulas, let’s just count this one out. If 4 flights left the airport between 9 and 10 A.M., then 8 left between 10 and 11 A.M., and 16 left between 11 A.M. and noon. Starting at noon, the flights begin to double every two hours, so 32 left between noon and 2 P.M., and 64 left between 2 P.M. and 4 P.M The correct answer is C. If you chose E, you may have forgotten to account for the afternoon change in the rate of increase, and the test writers, of course, made sure that the answer you came up with was there waiting for you.
3. D Since we have parallelograms, we really only have two angles, big ones and small ones, and we know that a big angle plus a small one equals 180. Statement (1) tells us the value of r; q, like r, is a small angle, so q + r = 70 + 70, or 140. We’re down to A and D.
Statement (2) gives us the value of a big angle, which we can subtract from 180 to get the value of a small angle. We now have the same information we had in Statement (1) and our answer is D.
4. D This is a Plugging In problem. Since it’s a percent problem, too, and the question asks us to find a percentage greater than the mileage of Stan’s SUV, let’s make Stan’s mileage 100. Chris’s mileage is therefore 140; 15% of 140 is 21, so Harry’s mileage is 161. 161 is 61% greater than 100, and the correct answer is D.
Answer choices A and C are both traps, since they’re simple addition and subtraction, respectively, of the numbers in the problem. If you got B, you probably increased Chris’s mileage by 15% of 40, rather than 15% of 140.
5. D Start by translating the two original equations: x = 3z + 1 and y = 2z – 1. If z is 4, then x = 13 and y = 7. 2x is thus 26 and 3y is 21. The difference between the two values is 5, so the correct answer is D.
If you chose A, you may have mistakenly added when the problem asked for a product. If you got E, you may have solved for x – y when the problem asked for 2x – 3y. And if you got C, you may have done both.
6. B Statement (1) tells us the difference between the numbers of employees at the two companies. Without the actual number of employees at either company, though, this information isn’t sufficient to answer this yes-or-no question, so we’re down to B, C, or E.
Statement (2), on the other hand, gives us the part-to-whole relationship we need to solve for the actual number of employees at each of the companies. We therefore know we can answer the question with a definitive “yes” or “no”—it doesn’t matter which one is actually correct—so the answer is B.
(If you really want to crunch the numbers, that 12.5% at Company A is the same as  , and Company A had 24,000 employees; that 20% at Company B is the same as
, and Company A had 24,000 employees; that 20% at Company B is the same as  , and Company B had 12,500 employees. The answer to the original question is “no”; Company A did not have more than twice the number of employees as did Company B.)
, and Company B had 12,500 employees. The answer to the original question is “no”; Company A did not have more than twice the number of employees as did Company B.)
7. E The question “Is x3 equal to 125?” can be rewritten as “Is x = 5?” This is a yes-or-no question, and the best way to tackle it is to Plug In twice. In Statement (1), we can plug in 5, in which case the answer to the question “Is x3 equal to 125?” is “yes.” Or, we can plug in 6, in which case the answer is “no.” Thus, because we get two different answers depending on the numbers we plug in, Statement (1) is not sufficient. We’re down to B, C, or E.
In Statement (2), we can plug in 5, in which case the answer is “yes,” or 4, in which case the answer is “no.” Eliminate B.
To see if the answer is C, we must choose a number that satisfies the conditions of both Statements (1) and (2) at the same time. We can plug in 5, in which case the answer is “yes.” You might have been tempted to choose C at this point because no other integer will satisfy the two equations at the same time, but does this problem limit us to picking integers? Nope. What about 4.5? Or 5.2? In either of these cases, the answer is “no.” Because we get two different answers depending on what numbers we plug in, the combination of Statements (1) and (2) is not sufficient either, and the correct answer is E.
8. C When a geometry problem comes without a diagram, always start by drawing one of your own. In this case, your diagram should look like this:
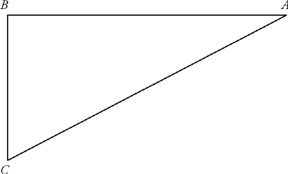
Statement (1) tells us the length of one side of our triangle, the distance from A to B. Since we know we have a right triangle (because Bob drove due west and due south), any two sides would be enough to find the remaining side. And if we knew that we had a “special” right triangle, one side might be enough. Neither of these cases applies, though, so we’re down to B, C, or E. Statement (2) gives us, again, a single side. Remember, though, that we can no longer consider the information from Statement (1), so this statement alone is also insufficient. We’re down to C or E.
When we put the 2 statements together, we know we could solve for the remaining side using the Pythagorean theorem—although, since this is a Data Sufficiency question, there’s no reason we would. The correct answer is C. Incidentally, if we did want to solve for the third side, we could save a lot of unnecessary calculation by recognizing this as a multiple of the old GMAT favorite, the 3-4-5 triangle. The two shorter sides of the triangle are multiplied by 6, so the remaining side must be 30.
9. B Although the relationship provided in the problem is based on geometry, this isn’t really a geometry problem for us: We can simply plug the given numbers into the formula. Starting with the larger rectangular solid,  =
=  =
=  = 13. For the smaller rectangular solid,
= 13. For the smaller rectangular solid,  =
= 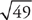 = 7. Both 13 and 7 are, of course, answer choices, but the problem asked us for the difference between the two values, so the correct answer is 6, choice B.
= 7. Both 13 and 7 are, of course, answer choices, but the problem asked us for the difference between the two values, so the correct answer is 6, choice B.
10. D This is a yes-or-no question, and we need to recognize that it’s not asking about the individual values of a, b, and c—it’s asking only about the average of those values. Of course, we could easily find the average if we knew the individual values. But, we can also find the average if we know the sum of the values, since the average of any group of values is their sum divided by the number of values in the group. Therefore, the question is asking us whether  = 8. To simplify this equation, multiply both sides by 3 to get a + b + c = 24. If the sum is 24, then the average is 8.
= 8. To simplify this equation, multiply both sides by 3 to get a + b + c = 24. If the sum is 24, then the average is 8.
Statement (1) tells us that 3(a + b + c) = 72. We can divide both sides by 3 to find out that the sum is, indeed, 24; the average is 8; and the answer to the question is “yes.” Since this is a Data Sufficiency problem, though, we can stop as soon as we know that we can find the sum of a, b, and c, and we’re down to A and D.
Statement (2) tells us that 2a + 2b + 2c = 48. If we factor a 2 out of the left side of the equation, we get 2(a + b + c) = 48 and once again see that we can find the sum. The correct answer is D.
11. B Since we should always calculate things inside the parentheses first—don’t forget PEMDAS!—start by adding 1 and  to get
to get 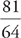 . Those are both perfect squares, so the inner root sign will be easy to handle:
. Those are both perfect squares, so the inner root sign will be easy to handle: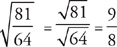 . Don’t grab answer choice C, though—we still need to work the outer sign:
. Don’t grab answer choice C, though—we still need to work the outer sign: . Like in high school, we can’t leave a radical on the bottom of a fraction, so we’ll need to multiply our answer by
. Like in high school, we can’t leave a radical on the bottom of a fraction, so we’ll need to multiply our answer by 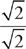 to get our final answer of B,
to get our final answer of B, 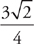 .
.
If you’re comfortable estimating fractions and roots, you can apply POE to this question. 1 +  is a little greater than 1; the square root of something a little greater than 1 is also something a little greater than 1; and the square root of that number is, again, something a little greater than 1. Only B and C are a little greater than 1.
is a little greater than 1; the square root of something a little greater than 1 is also something a little greater than 1; and the square root of that number is, again, something a little greater than 1. Only B and C are a little greater than 1.
12. D This is a fraction problem, so the key is to convert fractions to actual numbers. Statement (1) tells us that 1,250 people will take the stadium from 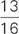 full to
full to  full; that’s a difference of
full; that’s a difference of  , or
, or  , so we know that 1,250 represents
, so we know that 1,250 represents  of the total seating capacity of the stadium. The stadium must, therefore, hold 8 × 1,250, or 10,000 people, and we’re down to A or D.
of the total seating capacity of the stadium. The stadium must, therefore, hold 8 × 1,250, or 10,000 people, and we’re down to A or D.
Statement (2) allows us to find a similar equivalence: a change of 2,500 represents the difference between 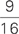 and
and 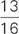 , that is,
, that is,  , or
, or  of the stadium’s total seating capacity. So we know we can find the total seating capacity (4 × 2,500, or 10,000 people) with Statement (2) as well, making D the correct answer.
of the stadium’s total seating capacity. So we know we can find the total seating capacity (4 × 2,500, or 10,000 people) with Statement (2) as well, making D the correct answer.
13. C Because there are fractions in the answer choices, and they’re fractions of an unspecified amount, the quickest way to solve this problem is to Plug In. Let’s make the price of Andre’s dream car $35—the denominators of the fractions in the problem are 7 and 5 (both factors of 35) and, moreover, 35 is in the denominator of all of the answer choices.
If the car costs $35, and Andre has already saved  of that, or $15, he currently has $20 left to save. Before the end of the summer he’ll be able to save
of that, or $15, he currently has $20 left to save. Before the end of the summer he’ll be able to save  of that remaining $20, or $8. That will give him a total of $23 saved toward his car, leaving him $12 to go. Expressed as a fraction of the cost of the car, that’s
of that remaining $20, or $8. That will give him a total of $23 saved toward his car, leaving him $12 to go. Expressed as a fraction of the cost of the car, that’s  , and the correct answer is C.
, and the correct answer is C.
As always, watch those trap answers. Choice D is the fraction of the cost that Andre will have saved by the end of the summer. Choice A is what you’d get if you calculated Andre’s summer earnings as two-fifths of the total cost of the car instead of two-fifths of what Andre has left to save. Choice E is what you’d get if you made both mistakes.
14. A The average of all four numbers is 6, so the numbers must add up to 6 times 4, or 24. That means y must equal 13. And if y equals 13, the median must be 5—that is, the average of the two middle numbers in the set. Even if y is very large, the middle numbers will still be 4 and 6, so choices D and E are much too large.
15. D If a six-pack sells for $2.70, then each can costs 45 cents when purchased together. When purchased individually, the price is higher than 45 cents, so cross off Choices A, B, and C. Let’s plug in Choice D. Choice D says the price of an individual can is 50 cents. 10% of 50 cents is 5 cents, so the price per can of a six-pack would be 50 – 5 = 45 cents. Therefore, choice D is correct.
16. A Covering up Statement (2) and looking only at Statement (1), we see that Beth saved one-third of her earnings and spent half of the two-thirds that remained on rent. Half of two-thirds is one-third. So we can set up the equation:
And x equals $1,200. Note that we didn’t actually need to find out how much Beth earned. We just needed to know that we could find out. We’re down to A or D.
Now, looking at Statement (2) we see that it tells us how Beth did THIS month. But do we care? Nope. The question asks us about LAST month. The correct answer is choice A.
17. B To answer this yes-or-no question, you must plug in values that make the statements true. Starting with Statement (1), let’s plug in 4 for n, which makes the statement “2n is an even integer” true, and gives us a “yes” to our overall question. Now, let’s plug in 3 for n, which still makes the statement true, but gives us a “no” to our overall question. Because the answer is sometimes yes and sometimes no, we’re down to BCE.
Looking at Statement (2) only, let’s plug in values that make the statement true. If n = 2, the statement is true, and the answer to our overall question is a tentative “yes.” Now, if we can find even one case where we can plug a number into this statement that makes the statement true but answers the question “no,” then we’ll be down to CE. But as you try different numbers, you’ll realize that in order to make Statement (2) true, n has to be even. So the answer to this question is B.
18. B Altogether, the percentages of men and women add up to 70%, so that means 30% of the residents at this complex are children. Just set up an equation:
Solving for x, the total number of residents is 80. The answer is B.
You could also Plug In the Answers. Choice C seems difficult, so why not start with choice B, which has an easy number to work with? 30% of 80 = 24. 40% of 80 = 32. So there are a total of 24 + 32 = 56 adults. If choice B is correct, there should be 24 kids. And guess what? That’s just what the problem says.
19. C If 30% of the players on the soccer team scored goals during the season, then 70% did not score goals. The ratio of those who scored to those who did not is 30 to 70, which reduces to 3 to 7.
Some will find that Plugging In is the easiest way to solve this problem. Plug in 10 for the number of players on the team (choose this number because it is easy to work with in a percentage problem). 30% of the 10 players—that is to say, 3 players—scored goals. The other 7, it then follows, did not score goals. The ratio of those who scored to those who did not is 3 to 7. The correct answer is C.
20. A Because Luis tipped the waiter 20%, we know that the sum of the check and tip equals 1.2 times the amount of the check. Thus, we can write the equation
1.2x = 16.80
and solve for x to determine both the amount of the check and the amount of Luis’s tip. The answer must be A or D.
Statement (2) is insufficient because it does not identify either the bills or the coins. The correct answer is A.
21. D According to Statement (1), the list price of the Leisure is  the list price of the Touristo. The list price of the Touristo is therefore greater than the list price of the Leisure. Statement (1) is sufficient; the answer must be A or D. Statement (2) tells you that the list price of the Touristo is 1.2 times the list price of the Leisure. So Statement (2) also tells you that the list price of the Touristo is greater than the list price of the Leisure. The correct answer is D.
the list price of the Touristo. The list price of the Touristo is therefore greater than the list price of the Leisure. Statement (1) is sufficient; the answer must be A or D. Statement (2) tells you that the list price of the Touristo is 1.2 times the list price of the Leisure. So Statement (2) also tells you that the list price of the Touristo is greater than the list price of the Leisure. The correct answer is D.
22. D If you look carefully at the drawing, you should notice that a and b are supplementary angles; that is, together they make up a line. The sum of these angles, therefore, is 180°. Or, to put this in math-speak:
a + b = 180
Now, return to the equation in the question stem, 3a = b. We can use this information to rewrite the equation a + b = 180 as
a + 3a = 180
4a = 180
a = 45
Because a + b = 180, and a = 45, b must equal 135, which is answer choice E. Wait, though, you’re not done yet: The question asks for the solution b – a. Because b – a = 135 – 45, the answer to this question is 90. The correct answer is D.
23. C Because there are an infinite number of multiples of 3, it is clear that Statement (1) is not sufficient to answer the question. The answer must be B, C, or E. Statement (2) narrows the range of possible answers to 421, 422, 423, or 424. However, because it does not narrow the answer to a single solution, it is not sufficient. Eliminate B.
When you put the two statements together, you know that w is a multiple of 3 that is either 421, 422, 423, or 424. Because only one of these values, 423, is a multiple of 3, the two statements together are sufficient. (A quick way to test whether an integer is divisible by 3 is to add its digits; if the sum of the digits is divisible by 3, then the number is divisible by 3.) The correct answer is C.
24. D Before we worry about the division, let’s solve for the two values. The second one is easier, so let’s start there: “of” means multiply, so 0.25 × 600 = 150. With the first value, we have to be sure to take into account both the decimal and the percent sign: 0.25% can be represented as  , or 0.0025. Either way, when you multiply by 600, the result is 1.5. The quotient is thus 1.5 divided by 150, or 0.01. The answer is D.
, or 0.0025. Either way, when you multiply by 600, the result is 1.5. The quotient is thus 1.5 divided by 150, or 0.01. The answer is D.
If you’re really comfortable with manipulating fractions, you can save yourself a lot of math. The whole question translates into  , which easily cancels down to
, which easily cancels down to  , or 0.01.
, or 0.01.
25. B Although you could solve this by writing a pair of algebraic equations (f + m = 21 and f = m – 3), it’s simpler to Plug In the Answers. Start with answer choice C, 7 men. The number of women would be 3 less than 3 times that number, or 21 – 3 = 18 women. That’s a total of 25 council members altogether, and we’re looking for 21. Now that we know that C is too big, we can eliminate answer choices C, D, and E.
If we try answer choice B, 6 men, then we have 18 – 3 = 15 women. This gives us our desired total of 21 council members, so the correct answer is B. If you got E, by the way, you solved for the number of female members on the board.
26. B Statement (1) tells you how many hours Vincent spends chopping down trees in a day, but it provides no data to help you determine how long it takes him to chop down 4 trees. This statement is clearly insufficient to answer the question. The answer must be B, C, or E.
Statement (2) tells you that Vincent takes twice as long as Roger to chop down trees. Because the question stem tells you that Roger chops down 4 trees per hour, you can deduce that Vincent chops down 4 trees every 2 hours. Thus, Statement (2) is sufficient to answer the question. The correct answer is B.
MATH BIN 2
EXPLANATIONS
1. C You could start by converting all the fractions to their least common denominator of 81—an understandable temptation. However, in this case, it’s quicker and simpler to reduce the fractions instead. They all reduce to  , so x =
, so x =  , or
, or  …or
…or  . Now that we know the value of x, we can solve for
. Now that we know the value of x, we can solve for  =
= 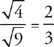 . The correct answer is C. Answer choice B, of course, is x itself, and answer choice D is
. The correct answer is C. Answer choice B, of course, is x itself, and answer choice D is  .
.
2. B This is a multi-step average problem involving an unknown quantity—in short, a perfect place to Plug In the Answers! Start with answer choice C: If Steven has already driven 6 laps, then we know that he has driven for a total of 6 × 51, or 306, seconds. One more lap in 39 seconds would give him a total of 7 laps in 345 seconds, and our average works out to be a little greater than 49 seconds (49 , to be exact). Close, but not quite. We need fewer laps to bring down Steven’s average speed, so answer choice B is the next logical choice. Five laps in 51 seconds means Steven has driven 5 × 51, or 255, seconds so far, and the additional 39-second lap gives us a total of 6 laps driven in 294 seconds. The average is now
, to be exact). Close, but not quite. We need fewer laps to bring down Steven’s average speed, so answer choice B is the next logical choice. Five laps in 51 seconds means Steven has driven 5 × 51, or 255, seconds so far, and the additional 39-second lap gives us a total of 6 laps driven in 294 seconds. The average is now  = 49 seconds, and B is the correct answer.
= 49 seconds, and B is the correct answer.
3. C Although you could solve this problem with lots of tedious multiplication, it’s much faster to recognize the quadratic equation hidden in the numbers: x2 – 2xy + y2 = (x – y)(x – y). That means we can rewrite the equation as (200 – 199) (200 – 199), or (1)(1). The correct answer is C.
Since the answer choices vary so widely, you may have been able to apply POE to the most extreme answer choices, A and E. The product of 200 and 199, which we have to double, is not too different from either 2002 or 1992. Thus, the negative value in the equation is roughly equal to the sum of the two positive values in the equation. If you did the math, by the way, and got one of those answers, you must have reversed an addition or subtraction sign.
4. A Since this problem has variables in the answer choices, the simplest way to solve it is to plug in. If x = 2, the equation becomes  = 13. Now plug 2 in for x in the answer choices—only answer choice A gives us 13, so it must be the correct answer.
= 13. Now plug 2 in for x in the answer choices—only answer choice A gives us 13, so it must be the correct answer.
And if you are feeling algebraic on this problem, there’s yet another approach that’s simpler than trying to factor the top of the fraction: Plugging In the Answers. Try multiplying your answer choices by the expression on the bottom of the fraction and see which one yields the expression on the top. Only answer choice A does, so it must, again, be the correct answer.
5. B Take a moment to translate what this question is really asking: Is the distance Amy drove greater than 120 miles? This rate problem is also a yes-or-no question, so we don’t need to know Amy’s exact speed, just if her average speed was greater than 60 miles per hour. The simplest way to find out whether Statement (1) is sufficient is to try different possible times and distances. If her total driving time was, for instance, 1 hour, a distance of 61 miles would yield an answer of “yes.” Meanwhile, a distance of 59 miles would yield an answer of “no.” That means we’re down to B, C, or E.
Regardless of what times and distances you plug in for Statement (2), on the other hand, you will always get an answer of “yes.” Even if Amy were to have driven the full 2 hours and gone only 122 miles, she would be driving at a rate of 61 miles per hour; since she actually drove a greater distance in less time, her rate must really be greater than 61. Since Statement (2) always gives us the same answer, it must be sufficient, and our answer is B.
6. A Once you’ve solved for x, which equals – , this question is just a matter of putting the four values in order. Even better, you already know two of them: x = –
, this question is just a matter of putting the four values in order. Even better, you already know two of them: x = – and x0 = 1. With the other two values, be especially careful about the negative sign: x2 =
and x0 = 1. With the other two values, be especially careful about the negative sign: x2 =  and x3 = –
and x3 = – . The correct order, then, is x0 > x2 > x3 > x1, and the answer is A.
. The correct order, then, is x0 > x2 > x3 > x1, and the answer is A.
7. B The information in Statement (1), along with that in the question itself, is enough for us to find the number of tickets issued for each show. Without any information about the number of those tickets that were sold, though, we can’t answer the question, and we’re down to B, C, or E.
Statement (2), along with the information in the question, is sufficient—even without the information in Statement (1). If we have the fraction of each type of ticket that was sold, and the ratio of one type of ticket to the other, we can figure out the overall percentage of tickets sold. The correct answer is B.
Want to prove it? Try Plugging In. In Statement (2), the denominator of both of our fractions is 5, so let’s say that 25 tickets have been issued for the afternoon show and 50 have been issued for the evening show. That means 15 tickets have been sold for the afternoon show and 10 have been sold for the evening show, for a total of 25 tickets sold out of a total of 75 tickets issued. The answer is  , as it will always be if we meet the requirements of Statement (2) and the question itself.
, as it will always be if we meet the requirements of Statement (2) and the question itself.
8. C First, solve for y. Since 2 =
=  ,
,  =
=  and thus y =
and thus y =  . Now plug the value of y into the equation:
. Now plug the value of y into the equation:
The correct answer is C.
Answer choice B, of course, is y itself. If you chose D, you forgot to flip over your final fraction. If you chose A, you forgot to add 1 when you put y in the equation. And if you chose E, you did both.
9. A Answering a function problem on the GMAT is simply a matter of following the directions provided as the definition for the function. In this case, the operation signified by two numbers with the ~ between them is defined as the sum of the numbers on either side of the ~ sign divided by the square of the product of the two numbers. If a ~ c = 0, then  = 0; since the numerator must be zero in order for the fraction itself to equal zero, we know that a + c = 0. Subtract a from both sides and c = –a. The answer is A.
= 0; since the numerator must be zero in order for the fraction itself to equal zero, we know that a + c = 0. Subtract a from both sides and c = –a. The answer is A.
10. C The easiest way to determine whether Statement (1) by itself is sufficient is to plug in different values for x. If x = 2, the greatest common factor is 2, and the answer to this yes-or-no question is “yes.” If x = 7, on the other hand, the greatest common factor is 1, and since 1 is not prime, the answer is “no.” We’re down to B, C, or E. Statement (2) by itself is also not sufficient. If x is equal to 1, 2, or 3, then the greatest common factor of x and 150 is x itself. But since 2 and 3 are prime, and 1 is not, we’re down to C and E. When we put the statements together, the only possible values for x are 2 and 3. With either one, the greatest common factor is equal to x itself and is, therefore, prime. The correct answer is C.
11. B As with all probability problems, we’ll have to find a fraction that has the total number of possibilities in the denominator and the number of those possibilities that meet a certain requirement in the numerator. The denominator is the easy part: Because there are 4 members of each set, there are 4 × 4 = 16 total possibilities for  . Now we just have to figure out how many of those possibilities meet the requirement.
. Now we just have to figure out how many of those possibilities meet the requirement.
The requirement, in this case, is that  is an integer—in other words, that x is divisible by y—and we can count out all of the combinations that meet that requirement quickly and easily. The first member of Set X, 9, is only divisible by one member of Set Y, 3, so that’s one. Then, working through Set X: 10 is divisible by both 2 and 5, so there’s another two; 11 is prime, and so it’s not divisible by any members of Set Y; and 12 gives us another three, because it’s divisible by 2, 3, and 4. Thus, 6 of our total of 16 possibilities meet our requirement, and our probability is
is an integer—in other words, that x is divisible by y—and we can count out all of the combinations that meet that requirement quickly and easily. The first member of Set X, 9, is only divisible by one member of Set Y, 3, so that’s one. Then, working through Set X: 10 is divisible by both 2 and 5, so there’s another two; 11 is prime, and so it’s not divisible by any members of Set Y; and 12 gives us another three, because it’s divisible by 2, 3, and 4. Thus, 6 of our total of 16 possibilities meet our requirement, and our probability is  , or
, or  . The answer is B.
. The answer is B.
12. B Since Statement (1) doesn’t tell us anything about the value of q, and very little about the value of p, it is, by itself, insufficient to answer this yes-or-no question. Statement (2), though, while it gives us no new specifics about the values of p or q, gives us enough information to know the answer to the question. Algebraically, if p = q, then  since we know from the question that p is an integer, the answer to the question is “yes,” and our answer is B. Of course, we can easily show the sufficiency of Statement (2) by plugging in values for p and q: as long as the values are equal integers, our answer is always “yes.”
since we know from the question that p is an integer, the answer to the question is “yes,” and our answer is B. Of course, we can easily show the sufficiency of Statement (2) by plugging in values for p and q: as long as the values are equal integers, our answer is always “yes.”
13. D Although this may seem like a volume question, it’s really about being able to fit the diameter of the satellite inside the crate—we can entirely disregard the given formula for the volume of a sphere. Let’s start with what we know: Since the radius of the sphere is 4, the diameter is 8. Therefore, every dimension in our crate must be at least 8 and the smallest available crate will measure 8 × 10 × 12. The volume of that crate is 960, and the correct answer is D.
In fact, if we try to use the volume formula we can easily go astray. Using a rough value of 3 for π, we can approximate the value of the sphere to be a little bigger than 250 (replacing π with 3 in the formula gives a value of 256, and the exact value is a little larger than 268). We might be tempted, therefore, to select answer choice C, but we can’t: The only set of three consecutive integers that would yield a volume of 480 would be 6 × 8 × 10, and we can’t put a spherical object with a diameter of 8 feet into a crate that’s only 6 feet across in one direction.
14. B This problem could be an algebraic nightmare, so let’s Plug In the Answers. We’ll start with answer choice C, 12. If David was 12 years old 4 years ago, he’s 16 now, and that means Richard is 22 and Scott is 8. In 8 years, then, Richard will be 30 and Scott will be 16; since Richard won’t be twice as old as Scott at that point, this can’t be the answer.
Run answer choice B, 10, through the same process. If David was 10 years old 4 years ago, he’s 14 now, so Richard is 20 and Scott is 6. In 8 years, then, Richard will be 28 and Scott will be 14; since Richard will then be twice as old as Scott, our answer is B.
15. E Statement (1) is a quadratic equation, so let’s factor it and see what our options are for x: x2 – 5x + 4 = 0 factors into (x – 4)(x – 1) = 0, so x could be 4 or 1. Since we can’t get a single value for x, Statement (1) alone is insufficient, and we’re down to B, C, or E.
Statement (2) alone leaves us with the vast majority of all numbers in existence—definitely not sufficient, so we’re down to C or E.
When we combine the statements, they’re still not sufficient. Be careful not to fall for one of the classic GMAT traps: 1 is not prime. Because, of course, neither is 4, we’re left with both values, and the correct answer is E.
16. E The probability that Sam will be chosen is  . The probability that Jessica will be chosen is also
. The probability that Jessica will be chosen is also  . The probability that they will both be chosen is
. The probability that they will both be chosen is  times
times  or
or 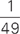 . This happens to be choice A, but we aren’t done yet. The question asks for the probability that they will NOT both be chosen. The probability that an event does NOT happen can be expressed as 1 minus the probability that the event DOES happen. So 1 minus
. This happens to be choice A, but we aren’t done yet. The question asks for the probability that they will NOT both be chosen. The probability that an event does NOT happen can be expressed as 1 minus the probability that the event DOES happen. So 1 minus 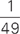 equals
equals  , or choice E.
, or choice E.
17. E Whenever you see a geometry problem without a diagram, it’s a good idea to make one. Statement (1) only tells us two of the three dimensions we need to find the surface area. We’re down to BCE.
Statement (2) tells us the area of another face of the rectangular solid. If this were a square, Statement (2) would be sufficient by itself, but it’s not, so we’re down to C and E.
Putting the two statements together, you might be tempted to pick C because we know the area of two different faces of the rectangular solid. But what if the two faces are facing each other? We still don’t know the third dimension of the rectangular solid, and the answer must be E.
18. E Before you do any fancy math, it is always helpful to think about what is reasonable. The probability that the number 6 is going to come up three times in a row is pretty low—another way of saying that the probability that 6 is NOT going to come up three times in a row is pretty high. So we can eliminate choices A, B, and C. Now, let’s figure out the problem. The probability that the first roll will yield the number 6 is  . The probability that the second roll will yield the number 6 is also
. The probability that the second roll will yield the number 6 is also  . The probability that the third roll will yield the number 6? You guessed it:
. The probability that the third roll will yield the number 6? You guessed it:  . To find the probability of the series of these three events happening, you multiply the probabilities of each of the individual events:
. To find the probability of the series of these three events happening, you multiply the probabilities of each of the individual events:  ×
×  ×
×  =
= 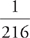 . That’s choice A, but we aren’t done yet.
. That’s choice A, but we aren’t done yet. 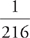 is the probability that the number 6 WILL face up on all three rolls. The probability that an event does NOT happen can be expressed as 1 minus the probability that the event DOES happen. So 1 minus
is the probability that the number 6 WILL face up on all three rolls. The probability that an event does NOT happen can be expressed as 1 minus the probability that the event DOES happen. So 1 minus 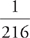 equals
equals  . The correct answer is choice E.
. The correct answer is choice E.
19. C Gut instinct may lead to you select E on this one; after all, Statement (1) provides a three-variable equation, which everyone knows is unsolvable. Statement (2) only refers to two of the three variables mentioned in the question stem, so clearly it cannot be sufficient. At first glance, it may be hard to imagine how the two statements together could be any more helpful than each is on its own.
Statement (1) is, in fact, insufficient on its own, for the reason stated above. Eliminate A and D. Statement (2) is also insufficient, again for the reason stated above. Eliminate B. The answer must be C or E.
Why is C the correct answer? If you add the two equations provided by (1) and (2), you get 3x + 3y +3z = 75. Factor a 3 out of both sides of the equation and you end up with x + y + z = 25. Thus, the two statements together are sufficient to answer the question “What is the sum of x, y, and z?” The correct answer is C.
20. D To answer this question, break the problem down into small, manageable steps. The first job at hand is to determine the selling price of the shirt, both during the first month they were on sale and then after. Because the store bought 1,000 shirts for $9,000, the cost of each shirt was $9.00. The store sold the shirts at an 80% markup during the first month. 1.8 × $9.00 = $16.20, so during the first month, the shirts sold for $16.20 each. After the first month, the selling price was 20% above cost. 1.20 × $9.00 = $10.80, so that was the selling price after the first month.
The store sold 75% of the shirts during the first month. 75% of 1,000 is 750; the store sold 750 shirts at $16.20 each. 750 × $16.20 = $12,150. Note that this partial answer is answer choice C. Test takers who only half-finish their work will choose this incorrect answer. The store then sold 50% of its remaining stock at $10.80 per shirt. The remaining stock is 250 shirts (1,000 – 750), half of which is 125. The store, then, sold 125 shirts at $10.80 each. 125 × $10.80 = $1,350. The store’s gross income from the sale of these shirts, then, was $12,150 + $1,350 = $13,500. The correct answer is D.
21. B Statement (1) provides information only about the sum of the balances on David’s EverywhereCard and his American Local card. Therefore, the statement is insufficient to determine whether the balance on David’s EverywhereCard is his highest balance, because it does not provide any information that allows you to compare the balance on the EverywhereCard to the balances on the other two cards. Eliminate A and D. Statement (2) tells you that the balance on David’s EverywhereCard is greater than the balance on his Passport card and less than the balance on his American Local card. Thus, it provides enough information to answer the question “Does David owe the greatest balance on the EverywhereCard?” The correct answer is B. There are a couple of places where you can go wrong on this question. The first involves the fact that Statement (2) answers the question this way: “No, he does not owe the greatest balance on the EverywhereCard.” Some test takers get confused and use a “No” answer to eliminate a statement. Remember, it doesn’t matter how you answer a yes-or-no question, just so long as you can answer it conclusively.
Some test takers might realize that Statements (1) and (2) together provide enough information to calculate the exact balance on each credit card, and thus may choose C. But because Statement (2) is sufficient on its own, C cannot be the correct answer to this question.
22. D To solve this problem, we need to write some equations. Let’s call Automobile A’s current speed A and Automobile B’s current speed B. The question stem tells us that A =  B. Statement (1) tells us that A + 10 =
B. Statement (1) tells us that A + 10 =  (B + 10). Thus, between the question stem and Statement (1), we have two non-identical equations, which means we can solve for our two variables. (Best of all, because this is a data sufficiency question, just knowing this is enough; we don’t have to actually solve it!) Rule out B, C, and E.
(B + 10). Thus, between the question stem and Statement (1), we have two non-identical equations, which means we can solve for our two variables. (Best of all, because this is a data sufficiency question, just knowing this is enough; we don’t have to actually solve it!) Rule out B, C, and E.
Statement (2) tells us that A − 10 =  (B − 10). Once again, we have two non-identical equations and two variables. Statement (2) is sufficient, and the correct answer is D.
(B − 10). Once again, we have two non-identical equations and two variables. Statement (2) is sufficient, and the correct answer is D.
23. D What makes this problem tricky is the presence of decimals, so the best thing to do is to get rid of them right off the bat. Multiply both sides of the equation by 100 to produce the equation 35a = 20b. (If you don’t multiply both sides carefully, you could end up with answer E.) Now, you can Plug In, or simply solve for b by dividing both sides by 20 to get b =  a. Convert the fraction to a decimal by dividing 35 by 20 to yield b = 1.75a. The correct answer is D.
a. Convert the fraction to a decimal by dividing 35 by 20 to yield b = 1.75a. The correct answer is D.
24. A You could solve this problem algebraically, but do you really want to? Plugging In the Answers is so much easier! Let’s start with answer C, because it’s the middle value among the answer choices. If this is the correct answer, then the Binary Ice Cream Shoppe sold 42 vanilla cones on Friday. Because vanilla cones sold at a 2-to-3 ratio to chocolate cones, this would mean that the shop sold 63 chocolate cones  . If this is the correct answer, then the ratio of (42 + 4) to 63 would be 3 to 4. It is not, so this answer must be incorrect.
. If this is the correct answer, then the ratio of (42 + 4) to 63 would be 3 to 4. It is not, so this answer must be incorrect.
You must decide next whether the correct answer is more or less than 42. If you have good math instincts, you’ll know it’s less because of the result that answer C yielded. If you aren’t sure, just pick a direction and go; you’ll find the correct answer soon enough either way. Note that the answer cannot be B because B is an odd number. Because it is not divisible by 2, it cannot be the number of vanilla cones sold. A is the correct answer. 32 to 48 is a 2-to-3 ratio; add 4 more vanilla cones to get a ratio of 36 to 48, which reduces to 3 to 4.
25. A In order to answer this yes-or-no question correctly, you must remember that 2 is a prime number. If you forget that, you are lost. Statement (1) tells us that 2a has exactly 3 factors. Let’s plug in some numbers. If you choose 3 for a, then 2a = 6. What are the factors of 6? 1, 6, 2, and 3. In other words, there are 4 factors. Is there any number we can plug in for a that gives us only 3 factors for the number 2a? As a matter of fact, there is only one: 2. Only 2 times 2, or 4, has exactly three factors: 1, 2, and 4. This tells us that a must be 2; any other multiple of 2 would have at least 4 factors (itself, 1, 2, and the product of itself and 2.) So if a can only be 2, can we definitely answer this yes-or-no question? Yes, 2 is a prime number.
Statement (2) is tempting for several reasons. If you forgot that 2 is prime, you would incorrectly conclude that this statement alone is sufficient to answer the question “No.” If you figured out that a = 2 from Statement (1), you may be tempted to choose this because it confirms the information given in Statement (1). However, because it is not sufficient to answer the question on its own, you must resist temptation. The correct answer is A.
26. E Solve this problem by plugging in values. Set m equal to a value that will transform the question into an easy arithmetic problem. For example, m = 40 is a good, easy value. It tells us that Renee can ride 1 mile every 2 minutes. How many miles, then, can she ride in 10 minutes? She can ride 5 miles in 10 minutes.
Now, plug in 40 for m in each of the answer choices. The correct answer will calculate to 5, the value of x when m = 40. Because E is the only answer that equals 5, E is the correct answer.
27. C You can solve this yes-or-no problem by plugging in values to test the answer choices. However, before you start doing that, you can eliminate several answer choices.
Statement (1) by itself clearly is not sufficient to answer the question, because it tells us nothing about w. Eliminate A and D. Is Statement (2) sufficient? Let’s plug in values. w could equal 5, because 5 + 3 = 4s can be solved in a way that satisfies the rules of this question (i.e., that s and w are integers). Thus, Statement (2) might be sufficient to tell us that  is an integer. Wait a minute, though: w could also equal 13, because 13 + 3 = 4s is also solvable. Because
is an integer. Wait a minute, though: w could also equal 13, because 13 + 3 = 4s is also solvable. Because  is not an integer, Statement (2) is not sufficient. Sometimes it answers “yes,” other times it answers “no.” Eliminate B.
is not an integer, Statement (2) is not sufficient. Sometimes it answers “yes,” other times it answers “no.” Eliminate B.
What about when we put the two statements together? Here, a little algebra illustrates the correct answer very elegantly. Statement (2) tells us that 4s = w + 3; use this information to rewrite Statement (1) as w + 3 + 2 is divisible by 5. Thus, w + 5 is divisible by 5. Any number that is divisible by 5 when you add 5 to it is divisible by 5 on its own; if you don’t believe it, plug some values in for w and prove it to yourself. The correct answer is C.
MATH BIN 3
EXPLANATIONS
1. B We don’t need to worry about that range for the initial discount: Since we want the lowest possible price, we want the greatest possible discount. Thirty percent of 260 is 78, so the price after the initial discount is $260 – $78, or $182. The additional 20% discount amounts to $36.40—remember, the 20% discount is 20% of the already-discounted price. $182 – $36.40 = $145.60, and the correct answer is B.
2. D This problem never specifies the cost of a gallon of gas, so let’s Plug In $1. Kim, then, paid $1 per gallon for the first 10 gallons and $0.90 per gallon on the next 10; that’s a total of 20 gallons for $19, an overall average of $0.95 per gallon, and a total per-gallon discount of 5 cents. Isabella paid $1 per gallon for the first 10 gallons and $0.90 per gallon on the next 15; that’s a total of 25 gallons for $23.50, an overall average of $0.94 per gallon, and a total per-gallon discount of 6 cents. The question asks us to relate Kim and Isabella’s total per-gallon discounts, so 5 and 6 cents, respectively. Six is 120% of 5, and the correct answer is D. You might have applied POE to answer choices A and B: Since Isabella bought more gas at the discounted rate than did Kim, Isabella’s discount is greater than, and therefore more than 100% of, Kim’s.
3. A Statement (1) is sufficient, by itself, to answer the question. Although we can’t determine, from Statement (1), the individual areas of the two triangular shaded regions, when combined they equal 27 (half of the total area of rectangle ABCD). The easiest way to see this is to draw a vertical line through point E, cutting the rectangle into two smaller ones. Now we have two rectangles that are divided by diagonals, and diagonals, by definition, cut rectangles in half. If half of the two smaller rectangles are shaded, then so is half of the larger rectangle. We’re down to A and D.
Statement (2) gives us the relationship between the two smaller shaded regions, but it doesn’t alone allow us to determine anything about their individual areas. Statement (2) is insufficient, and the correct answer is A.
4. C Statement (1) is, by itself, insufficient to answer the question, although it does provide the very useful information that r = q. If you’re comfortable working with triangles, you may have immediately read “180 minus the sum of p and r” as being equal to q. If not, you can discover this using algebra, though the route is a bit more arduous. Add (p + r) to both sides to yield r + p + r = p + q + r; but since p + q + r also equals 180, you can combine the equations to get r + p + r = p + q + r. Subtract a p and a q from each side, and you’re left with r = q. Nonetheless, this is still insufficient to answer the question. If r and q are both 60, the answer is “yes”; if they’re both 45—remember, you can’t trust the diagrams in Data Sufficiency—the answer is “no.” We’re down to B, C, or E.
Statement (2), by itself, is also insufficient to answer the question; the only thing it tells us about q and r is their sum, which equals 120. Eliminate B.
When we combine our statements, though, we can determine whether the triangle is equilateral. If r and q are equal and their sum is 120, then they, like p, must equal 60. If all three angles equal 60, the triangle must be equilateral, and the correct answer is C.
5. D Since the problem never specifies how many videos were rented during the two-week period, this is a good opportunity to plug in. Rather than plugging in a value for A and trying to determine the total number of videos rented—possible but problematic—let’s plug in an easy number, such as 100, for the total, and calculate the rest of the numbers from there.
If a total of 100 videos were rented in the two-week period, then 70 were comedies. Of the remaining 30, there were 5 times as many dramas as action movies, so that means 25 dramas and 5 action movies. We now know both our value for A, 5, and our target answer, 70. Only answer choice D yields 70 when 5 is plugged in for A, so D is the correct answer.
6. D Because the units digit of x2 is 6, the units digit of x must be either 4 or 6. Because x, y, and z are consecutive positive integers, the units digit of y must be 5 if the units digit of x is 4. However, the units digit of y can’t be 5 because the problem tells us that the units digit of y2 is 9; if the units digit of y were 5, then the units digit of y2 would also be 5. Therefore, the units digit of x is 6, the units digit of y is 7, and the units digit of z is 8. The units digit of z2, then, must be 4.
If that seems confusing, why not just Plug In? The units digit of x2 is 6. Let’s say x2 = 36, so x = 6. The units digit of y2 is 9, so let’s say y2 = 49 and y = 7. If x, y, and z are consecutive positive integers, that makes z = 8, and the units digit of z2 = 4.
7. D Statement (1) alone is sufficient to answer the question. Ordinarily, having one side of a right triangle isn’t enough to solve for all three sides. However, since two of the sides of our triangle are also radii of our circle, this is no ordinary right triangle: It’s an isosceles right triangle, also known as a 45-45-90 triangle. As such, knowing that the long side of the triangle is 8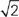 is enough to tell us that the short sides are both 8. Once we know the radius, we can solve for the area—64π, if you were wondering—and we’re down to A or D.
is enough to tell us that the short sides are both 8. Once we know the radius, we can solve for the area—64π, if you were wondering—and we’re down to A or D.
Statement (2) alone is also sufficient to answer the question. Arc ABC, since it’s subtended (or “cut out”) by a 90° angle, must represent  , or
, or  , of the entire circumference. That gives us an entire circumference of 16π; from the circumference, we can find the radius, 8, and from there the area. The correct answer is D.
, of the entire circumference. That gives us an entire circumference of 16π; from the circumference, we can find the radius, 8, and from there the area. The correct answer is D.
8. C Yet another question about an unspecified amount—in this case, the total number of students in the senior class—which means another opportunity to plug in. Since the answers are percentages, let’s plug in 100 for the total number of seniors. That means we have 60 females, of whom 70%, or 42, are going on the senior trip; they’ll be joined by 90% of the 40 males, which gives us 36 males on the trip. That’s a total of 42 + 36 = 78 students who are going on the trip. Seventy-eight out of our senior class of 100 is, of course, 78%, so the correct answer is C.
9. A To find the answer to this yes-or-no question, try Plugging In to the two statements, starting with the one number that you know is in the set: 3. Statement (1) gives us all the positive multiples of 3, which answers the question with a definitive “yes”. Statement (2) gives us all the negative multiples of 3, plus 0. The correct answer is A. Joe might have picked D.
10. D Since the answer choices are full of variables, this is a good place to plug in. Let’s make d = 10, c = 200 (a particularly helpful number, because it allows us to work the problem in whole dollar amounts), and x = 5. If Sarah had an average of 5 items per day delivered, then she had a total of 35 items delivered for the week. Multiplied by the 200 cents (or $2) charge per item, that’s a total of $70 in per-item charges. When we add that amount to the $70 total for the per-delivery charges—7 deliveries at $10 per delivery—we get a total of $140 for the week. Our target answer, then, is 140; only D gives us 140 when we plug our values into our answer choices, and, therefore, D is the correct answer.
If you got C, by the way, check your calculations for your target answer. You likely calculated the per-item charges as though x were the total, rather than the daily average, of the items delivered.
11. B Standard deviation is the measure of how greatly the individual elements in a data set vary from the arithmetic mean of the set. As a general rule, the more widely dispersed the data in a set, the greater the standard deviation.
You don’t need to know how to calculate standard deviation on the GMAT. You do need to know that standard deviation is measured from the arithmetic mean of a data set. If a data set has an arithmetic mean of 10 and a standard deviation of 2, then 8 and 12 are the values that are exactly one standard deviation from the arithmetic mean of the set.
In this problem, the standard deviation is 4, and the question asks for an interval that covers two standard deviations from the arithmetic mean of 46. It’s key here to remember that “two standard deviations” means two in each direction—that is, both above and below the mean. Thus, we need an interval that covers 2 × 4, or 8, from the mean in each direction: 46 – 8 = 38, so the bottom end of the interval is 38, and 46 + 8 = 54, so the top end of the interval is 54. The correct answer is B. If you chose A, by the way, you only accounted for the two standard deviations below the mean. If you chose E, you only accounted for the two standard deviations above the mean. And if you chose C, you forgot to take two in each direction.
12. B To solve this yes-or-no problem, your best bet is to plug in values that meet the requirements given in the statements to determine whether Plugging In always yields the same answer to our question.
For Statement (1), for example, we could plug in 4 for both a and b—that’s one easy way to make sure that every prime factor of b is also a prime factor of a—and since every number is a multiple of itself, our answer is “yes.” However, if we leave b = 4 but make a = 2, we can still meet the requirement of Statement (1)—4 has only one prime factor, 2, which is also a prime factor of 2—but now our answer is “no.” Since Statement (1) yields different answers, it’s insufficient, and we’re down to B, C, or E.
Similar attempts in Statement (2), however, will always yield the answer “yes.” We could, of course, again plug in 4 for both variables, and we have our first “yes.” If we leave b = 4, though, we can’t make a = 2, since 4 isn’t a factor of 2; a will have to be 4 (which we’ve already used), 4, 12, 16, or some other number that has 1, 2, and 4 as factors. Whichever one we pick, though, our answer is “yes”; Statement (2) is therefore sufficient, and the answer to the problem is B.
13. A We could solve this problem algebraically, although it’s a bit of a chore. If we assign x to represent the smallest integer in the set, then x + (x + 1) + (x + 2) + (x + 3) + (x + 4) = 265, so 5x + 10 = 265, 5x = 255, and x = 51. The five smaller consecutive integers are thus 51 through 55; we can now add our five larger consecutive integers, which must be 56 through 60. Our total is 290, and the correct answer is A.
A much simpler way to solve the problem, though, is to recognize that the difference between the sums of any two adjacent sets of five consecutive integers will be the same; we can, therefore, find this difference using much easier numbers, and then add this difference to the total given in the problem. The sum of the integers from 1 to 5 is 15, and the sum of the integers from 6 to 10 is 40; our difference, thus, is 25, and 265 + 25 = 290.
14. A Remember, you can always simplify before heading into the statements. If you have the equation a – b = c and want b, then you could simply write it as b = a – c. Now, consider Statement (1) on its own. It tells you that c + 6 = a; this information allows you to rewrite the equation in the question stem (a – b = c), substituting c + 6 for a to come up with the equation c + 6 – b = c. Simplify the equation by combining like terms. You will see that the c’s cancel out, leaving you with the equation b = 6. Statement (1) is sufficient, and the answer must be A or D. Statement (2) provides information about only one of the three variables in the original equation, so it cannot be sufficient on its own. The correct answer must be A.
15. D You could no doubt set up some kind of an equation here, but it’s much easier to Plug In The Answers. Let’s assume for a minute that the correct answer was choice C, 10. So now, just substitute 10 for y in the problem. The average of the numbers {3, 5, 9, 13, 10} is 8, but the median of those numbers is 9. Eliminate it. Can you tell which way to go, up or down? If you’re not sure, just pick a direction and try. Let’s assume for a minute that the correct answer was choice D, 15. The average of the numbers {3, 5, 9, 13, 15} is 9, and the median of those numbers is—Bingo!—also 9. We’re done. The correct answer is choice D.
16. C This is a permutation problem. Looking at Statement (1), it might seem enough to know that medals will be awarded for 1st, 2nd, and 3rd place. Unwary test takers might assume that there are 3 × 2 × 1 possible arrangements of medal winners. But until we know the number of runners, we don’t know enough. We’re down to BCE.
Statement (2) tells us the number of runners. An unwary test taker might either assume all runners get medals (in which case the answer would be 10! permutations) or subconsciously assume that we already know there are 3 possible medals and pick B, but we don’t know this without Statement (1). We’re down to C or E. Putting the two statements together, we can now find out how many different arrangements of medal winners there are: 10 x 9 x 8. The correct answer is C.
17. D The range of any data set is equal to the largest item in the set minus the smallest. Statement (1) gives us a value for the range. If that value were anything other than 0, we would not be able to solve the problem based only on this statement. After all, if the range was, say, 7, how could we know which of the three terms (x, y, or z) was the biggest and which was the smallest? However, because Statement (1) tells us that the range is 0, we actually know more than you might think about these three numbers. Because the problem tells us that x must equal 3, let’s plug in values for y and z, just to see what happens. For example, if y and z both equal 5, will the range still equal 0? Nope. It would have to be the largest number (5) minus the smallest (2). When you start plugging in numbers, you realize that the only way for the range of these three numbers to be 0 is if each of the numbers is exactly the same. And because we know x equals 3, that means both y and z must equal 3 as well. We’re down to AD.
Statement (2) tells us that all the values in the data set correspond exactly to the arithmetic mean—which tells us that x, y, and z are all equal to 3. The correct answer is choice D.
18. C In this combination problem, the employer’s choice of a programmer can be written as
The employer’s choice of a manager can be written as
To find the total number of ways she could make her selection, multiply the respective number of possibilities. 6 times 20 = 120. The correct answer is choice C.
19. C The question asks you for the hypothetical greatest number of animals that could have been adopted from the shelter within the parameters of the problem. Because a greater proportion of dogs than cats was adopted, you should seek a scenario that maximizes the number of dogs adopted. You must also satisfy the other conditions of the problem, however; the number of cats, for example, must be a multiple of 5, because that is the only way that  of the cats can be adopted (assuming, of course, that the shelter requires people to adopt an entire cat, not just a fractional part of one).
of the cats can be adopted (assuming, of course, that the shelter requires people to adopt an entire cat, not just a fractional part of one).
Because we want to maximize the number of dogs in the shelter, let’s start assuming the minimum possible number of cats, 5. This would leave 50 dogs in the shelter. This solution, unfortunately, is impossible; because 50 is not evenly divisible by 4, there cannot be 50 dogs in the shelter. Could there be 10 cats at the shelter? No, because this would leave 45 dogs, again making it impossible for exactly  of the dogs to be adopted. 15 cats is the magic number, as it means there are 40 dogs.
of the dogs to be adopted. 15 cats is the magic number, as it means there are 40 dogs.  = 3 + 10 = 13 animals. The correct answer is C.
= 3 + 10 = 13 animals. The correct answer is C.
20. A Because x is an integer, x must be either even or odd. If x is even, then x2 – x must also be even, and therefore x2 – x – 1 is always odd. If x is odd, then x2 – x must be even, and again, x2 – x – 1 is always odd.
You can also solve this problem by Plugging In. After plugging in several values for x and calculating x2 – x – 1, you will discover that the result is always odd.
21. D The question stem tells us that the average high temperature for the five-day period was 86°; therefore, the sum of the high temperatures for those days was 5 × 86 = 430°. Statement (1) tells us that the average high temperature for the first four days was 87°; therefore, the sum of the high temperatures for those days was 4 × 87 = 348°. 430 – 348 = 82°, the high temperature on Friday. Statement (1) is sufficient; the answer must be A or D.
Statement (2) tells us that Friday’s temperature reduced the average high for the five-day period by 1 degree. This means that the average high for the first four days was 87°; thus, (2) is sufficient for the same reason that (1) is sufficient. The correct answer is D.
22. A Don’t get caught making a careless assumption on this question. You may have immediately recognized that x2 – y2 factors to (x + y)(x – y). Seeing that Statement (1) provides a value for (x + y) and Statement (2) provides a value for (x – y), you might have automatically assumed that the correct answer to this question is C. Look more closely, however; Statement (1) tells you that (x + y) = 0. Zero times any number equals zero. Therefore, Statement (1) is sufficient to tell you that (x + y)(x – y) = 0. The correct answer is A.
23. D This is an excellent Plugging In problem. Plug in a value that is easily divisible by 3 for P; let’s use 18. That would make the length of each side of the equilateral triangle 6.

Draw a height for the triangle. Note that the height of an equilateral triangle divides the triangle into two 30–60–90 triangles, each with a base of 3.
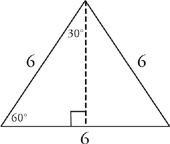
Now you can use the formula for the sides of a 30-60-90 triangle to determine that the height of the triangle is 3 when P = 18. Finally, simply plug in 18 for P in every answer choice and eliminate those that do not yield a result of 3
when P = 18. Finally, simply plug in 18 for P in every answer choice and eliminate those that do not yield a result of 3 . The correct answer is D.
. The correct answer is D.
24. E These problems are a lot easier to solve than they appear to be at first glance. Remember, when you’re done adding all these percentages, they have to add up to exactly 100. The numbers given us in the problem add up to 110. Why? Because some people are counted twice. Who are these people? Why, the folks who own bicycles AND automobiles, of course. They are the “extra” 10%. 65% of Americans own an automobile but no bicycle; 5% own only a bicycle; 10% own both; and 20% own neither. The correct answer is E.
25. D The formula for the area of a triangle, of course, is  . Therefore, if we know the ratio of the bases and the heights of these triangles, it would be safe to assume that we know enough to calculate the ratios of their areas. This makes C a very tempting answer, because Statement (1) provides the ratio of the heights of the two triangles and Statement (2) provides the ratio of the bases of the two triangles. Well, now, if it were that easy, it wouldn’t be in Bin 3, would it?
. Therefore, if we know the ratio of the bases and the heights of these triangles, it would be safe to assume that we know enough to calculate the ratios of their areas. This makes C a very tempting answer, because Statement (1) provides the ratio of the heights of the two triangles and Statement (2) provides the ratio of the bases of the two triangles. Well, now, if it were that easy, it wouldn’t be in Bin 3, would it?
The reason that the answer to this question is D lies in the special nature of isosceles right triangles and equilateral triangles. Their sides are in a fixed proportion to one another, so when you have information about one side, you have of information about all sides and, consequently, the area of the triangles. For this reason, each statement is sufficient on its own.
To prove that to yourself, you can plug in values for the sides of the triangles. For example, in Statement (1), the ratio of BC to EG is 1 to 1. So, let’s say BC and EG are both one meter long. Since ABC is isosceles, that means AC = 1, too, and the area of ABC is  . Since DEF is equilateral, that means DG and GF are each
. Since DEF is equilateral, that means DG and GF are each  and DF is 2
and DF is 2 . Therefore, we can find the area of DEF (
. Therefore, we can find the area of DEF ( ).
).
26. A The only one solution to the equation in Statement (1) is x = 3. (If this is unclear, review radicals in the Arithmetic section of this book.) Therefore, the answer to this question must be A or D.
To determine whether (2) is sufficient, subtract 2x + 8 from both sides of the equation to get
x2 – 2x – 8 = 0
This equation can be factored to
(x – 4)(x + 2) = 0
Thus, the equation has two solutions: x can equal 4 or –2. Statement (2) is not sufficient. The correct answer is A.
MATH BIN 4
EXPLANATIONS
1. C To answer this question, first recognize that the area of the walkway can be calculated by subtracting the area of the smaller (white) rectangle from the larger rectangle in the figure. The difference between the areas of the two rectangles equals the area of the shaded region. This problem is ideal for Plugging In The Answers. Start with answer choice C; if it is incorrect, you may be able to tell whether it is too large or too small, and you will be able to eliminate not only C, but also two other answers.
If C is correct, then the walkway is 5 feet wide. With a walkway of that width, the dimensions of the large rectangle in the figure are 30 feet (the width of the garden—20 feet—plus 5 feet on each side to account for the width of the walkway) by 40 feet (the length of the garden—30 feet—plus 5 feet on each side to account for the width of the walkway). The area of the large rectangle, then, is 40 × 30 = 1,200 square feet, and the area of the shaded region is 1,200 – (20 × 30) = 1,200 – 600 = 600 square feet.
When the width of the walkway is 5 feet, the area of the walkway equals the area of the garden. That’s the result we’re looking for, so the correct answer is C.
2. C As is often the case with difficult probability questions, the bottom part of our fraction—the total number of possibilities—is a permutation problem in itself. In this case, we need to figure out how many different outcomes we can get if we flip a coin 6 times. Since we have 6 events with 2 possible outcomes each, our total number of different outcomes is 2 × 2 × 2 × 2 × 2 × 2, or 26, or 64. Now we just need to figure out how many of those possibilities meet the requirement.
For this problem, however, since there are so many different ways to meet the requirement, we’ll be better off figuring out how many outcomes don’t meet our requirement; we can then subtract this number from the total of 64. There are only three ways to not meet the requirement of 2 to 5 tails on 6 flips—we could get 0, 1, or 6 tails—and these can be quickly and easily counted out. There is only one way to get 6 tails, and, likewise, there is only one way to get 0 tails, which is another way of saying 6 heads. That’s two. And there are only six different ways to get tails once: The single tails can come up in the first spot, the second spot, and so on. That’s 8 out of our total of 64 possible outcomes that don’t meet our requirement, so 56 do. The probability, therefore, is  , which reduces to
, which reduces to  . The correct answer is C.
. The correct answer is C.
3. C Statement (1) is not alone sufficient to answer the question. It does let us determine how many recruits will have to retake the test, but we don’t know anything about their scores. We’re down to B, C, or E. Statement (2) alone is also insufficient—while those 10 recruits are certainly impressive, we don’t know what part of the overall recruiting class they represent. We’re down to C or E.
When we combine our statements, though, we do have enough information to answer the question. We can now calculate that those 10 top-scoring recruits make up the top 2% of the class as a whole—and since the scores are normally distributed, the top 2% represents the third standard deviation above the mean. If the mean is 72, and the third standard deviation above the mean begins at 82, then there are 2 standard deviations (the first and the second) between 72 and 82. The dividing line between them, then, must fall at the score halfway between 72 and 82, or 77. We now know the entire upper half of the curve: The first standard deviation runs from the mean of 72 to 77; the second standard deviation runs from 77 to 82; and the third standard deviation runs from 82 to 87. More important, we now know that one standard deviation equals 5 points, so that bottom 16%—also known as the second and third standard deviation below the mean—are those that score at or below 67. The correct answer is C.
4. C To determine how many cards Jerome must draw to achieve his desired goal, determine the worst-case scenario. Let’s start by figuring out how many cards Jerome can draw whose face values, when multiplied, would not yield an even-numbered product. His first card, obviously, would have to be an odd-numbered card. If the second card he drew is an odd-numbered card, then the product of the drawn cards would be odd. If the third card he drew was odd, then the product would still remain odd. As long as Jerome kept drawing odd-numbered cards, he would not have a pile of cards whose face values would yield an even product. Thus, in the worst-case scenario, Jerome would draw all ten odd-numbered cards. At this point, the eleventh card would have to be even, which would make the product of the 11 cards even. Therefore, Jerome must draw 11 cards to ensure an even product. The correct answer is C.
5. E This is a yes-or-no question. Statement (1) tells us that three of the five integers are less than 50. This information by itself does not ensure that the other two integers are greater than 100. Both remaining values could be greater than 100; the solution set {10, 20, 30, 140, 300}, for example, satisfies this condition. However, the set {1, 2, 3, 4, 490} also satisfies the conditions of the problem, and it contains only one value greater than 100. Statement (1) is insufficient on its own; the correct answer must be B, C, or E. Statement (2) tells us only that none of the integers is equal to 100. By itself, this is clearly not sufficient to tell us that exactly two of the integers are greater than 100; eliminate answer B immediately. In fact, the statement provides no more useful information than that provided in Statement (1); both of the solutions provided above satisfy this statement as well. The purpose of this statement is to catch someone who might be tempted to choose C, thinking that Statement (1) would be sufficient if only it ensured that none of the remaining integers was equal to 100, and therefore must be greater than 100. That, of course, is an erroneous conclusion, as demonstrated by the counterexample provided in the previous paragraph. The correct answer is E.
6. B Statement (1) clearly is not sufficient to answer the question “How long is the route along which Paul jogs?” because it tells us only Paul’s starting time. The correct answer to this question must be B, C, or E. Statement (2) tells us that Paul had jogged 5 miles by 5:40 P.M. and 8 miles by 6:04 P.M. You might be tempted to answer C at this point; after all, you now know when Paul began jogging and how far he had jogged at various intervals, so you could easily figure out how far he had run by 6:20 P.M., the end of the 80-minute period beginning at 5:00 P.M. Resist the temptation; it is the voice of none other than Joe Bloggs himself telling you to choose C. Let’s look more closely at Statement (2). It tells us that Paul covered 3 miles between 5:40 P.M. and 6:04 P.M. Thus, we know that Paul ran eight-minute miles during that 24-minute period. The question stem tells us that Paul jogs at a constant rate, and that he jogs for 80 minutes. Therefore, Statement (2), in combination with the question stem, provides all the information we need; Paul jogs eight-minute miles for 80 minutes, so the route along which he jogs is 10 miles long. The correct answer is B.
7. B Because the problem has variables in the answer choice, Plugging In is a great way to solve. Plug in an easy number, one that will make your calculations and answer checking simple. For the purposes of this explanation, let’s set r equal to 2. With each rotation, each wheel rotates the length of its circumference. Thus, the wheel with diameter 40 centimeters rotates 40π centimeters with each rotation; the wheel with diameter 32 centimeters rotates 32π centimeters with each rotation. The larger wheel makes r revolutions per minute; because we’ve set r equal to 2, it makes 2 revolutions per minute and thus rotates 80π centimeters per minute. According to the problem, the smaller wheel must rotate the same distance; otherwise, the conveyor belt will not run smoothly. Therefore, the smaller wheel also rotates 80π centimeters per minute, meaning it rotates 60 × 80π = 4,800π centimeters per hour. The smaller wheel covers 32π centimeters per rotation, so it must rotate 4,800π ÷ 32π = 150 times per hour. Plug 2 in for r in each of the answer choices. Which yields an answer of 150? The correct answer is B, 75r.
8. C Create a table to solve this proportions question. It should look something like this:

The question stem tells us how many cars were sold last year. Because it tells us that half the cars sold were red, it also tells us the number of red and blue cars sold last year.
Statement (1) tells us: “The dealership sold three times as many blue coupes as red sedans last year.” Enter this information into the table in algebraic terms:

Because two unknowns—red coupes and blue sedans—remain, Statement (1) does not provide enough information to solve the problem. The correct answer must be B, C, or E.
Use the same procedure to test Statement (2): “The dealership sold half as many blue sedans as blue coupes last year”:

Again, two unknowns remain. This time, though, we have all the information we need to write a solvable equation. We know that 2x + x = 4,500. Therefore x equals 1,500. We now know the following:

Unfortunately, this still isn’t enough information to answer the question “How many coupes did the dealership sell last year?” The answer must be C or E. Combine the information from the two statements. Statement (2) tells us that the dealership sold 3,000 blue coupes; combined with Statement (1), this tells us that the dealership sold 1,000 red sedans. We can now subtract 1,000 from 4,500 to determine that the dealership sold 3,500 red coupes. Therefore, it sold 6,500 coupes last year. The correct answer is C.
9. A Solve this one using Plugging In. First, plug in a number of seats for the entire stadium. Choose a number that divides easily by 3, 4, and 5. For the purposes of this explanation, let’s say the stadium seats 60,000 people. The problem states that  of all the seating in the stadium was sold, meaning that 40,000 of the 60,000 seats were sold. It also states that
of all the seating in the stadium was sold, meaning that 40,000 of the 60,000 seats were sold. It also states that  of the seating is located in the lower deck. Because
of the seating is located in the lower deck. Because  of 60,000 is 15,000, that means the stadium has 15,000 seats in the lower deck. Of those 15,000 seats, according to the problem,
of 60,000 is 15,000, that means the stadium has 15,000 seats in the lower deck. Of those 15,000 seats, according to the problem,  , or 12,000, were sold. The question asks what fraction of the unsold seats in the stadium were in the lower deck. Because 40,000 seats were sold in the entire stadium, a total of 20,000 were unsold; of the 20,000 unsold seats, 15,000 – 12,000 = 3,000 were in the lower deck. The fraction
, or 12,000, were sold. The question asks what fraction of the unsold seats in the stadium were in the lower deck. Because 40,000 seats were sold in the entire stadium, a total of 20,000 were unsold; of the 20,000 unsold seats, 15,000 – 12,000 = 3,000 were in the lower deck. The fraction  reduces to
reduces to 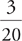 , so the correct answer is A.
, so the correct answer is A.
10. B Statement (1) provides no information about the non-executive employees at Company R. Clearly it is not sufficient on its own; the correct answer must be B, C, or E. Statement (2) provides a ratio of executive employees to non-executive employees at Company R. Is this information by itself enough to determine the average age of all the employees? Yes, it is. Regardless of whether Company R has 2 executives and 8 non-executives or 200 executives and 800 non-executives, the resulting average for all employees will be the same, because the proportional contribution of each group to the average will remain fixed. The best way to prove this is simply to plug in some numbers and see for yourself. The average age of 1 executive and 4 non-executives is  = 38. The average age of 30 executives and 120 non-executives is
= 38. The average age of 30 executives and 120 non-executives is  = 38. Thus, the correct answer is B. Joe Bloggs, by the way, picks C on this problem.
= 38. Thus, the correct answer is B. Joe Bloggs, by the way, picks C on this problem.
11. A Joe Bloggs probably told you to pick answer choice C on this problem. You knew better than that, though, didn’t you? Let’s look at Statement (1). It tells us that a, c, and x are negative. Instinctively, we might conclude that this isn’t enough information, because it tells us nothing about b or d. Look at the expression in the question stem again, though; b and d appear only in the expressions (bx)2 and (dx)4. Both of these expressions contain even exponents; we know, therefore, that these expressions must be positive regardless of the values b and d represent, because nonzero integers raised to an even power are always positive. From Statement (1) we know that ax is positive (a negative times a negative equals a positive) and, similarly, that (cx)3 is positive. Statement (1) is sufficient, and the answer must be A or D. For reasons already explained, Statement (2) provides no valuable information. The correct answer is A.
12. D According to the problem, an acceptable password consists of either DLDD or DDLD, where D represents a digit and L represents a letter of the alphabet. Remember also that the digits must be different. First, let’s consider DLDD. The first character can be any of the ten digits, 0 through 9. The second character can be any of the 26 letters of the alphabet. There are only 9 possible digits for the third character, because the third character may not repeat the digit used for the first character. By the same reasoning, there are only 8 possible digits for the fourth character. Thus, there are 10 × 26 × 9 × 8 = 18,720 possible passwords that follow the DLDD pattern. Now consider DDLD. There will be an equal number of possible passwords that follow this pattern. The first character can be any of 10 digits; the second character can be any of the 9 remaining digits; the third character can be any of the 26 letters of the alphabet; and the fourth character can be any of the remaining 8 digits.
10 × 9 × 26 × 8 = 18,720. There are 18,720 + 18,720 = 37,440 different passwords possible, and the correct answer is D.
13. E This is a yes-or-no question, of course. If we plug in numbers for x in Statement (1), we will sometimes get a “yes” (by plugging in, for example, 48) and sometimes get a “no” (by plugging in, for example, 16), so we are down to BCE. The same is true with Statement (2). After all, some—but not all—numbers divisible by 6 are also divisible by 48, so Statement (2) also gives us both yes and no answers. The answer must be C or E. Which answer do you think Joe Bloggs would pick? C, probably, because 48 is the product of 6 and 8. He would probably carelessly conclude that any number divisible by both 6 and 8 must also be divisible by 48, thus answering the question with a “yes.” Unfortunately, Joe doesn’t think about 24, 72, and a whole host of other numbers that are divisible by 6 and 8 but not by 48. Even when we combine both statements, the answer to the question is sometimes yes and sometimes no. Therefore, the correct answer is E.
14. A At first it looks as though you’ll have to substitute every odd digit for the three variables until you stumble onto the correct answer, but there’s a trick to this problem that eliminates such guesswork. Look at the units column of the problem and you’ll see that F × G yields a product with a units digit of G; therefore, it is quite possible that F is the identity element, 1. Actually, you can go even further: F must equal 1, because G cannot equal 1 (otherwise, the product of this multiplication problem would be FGF, not HGG). Plus, if both F and G were odd digits greater than 1, the product of this multiplication problem would be a four-digit number. Because the product is the three-digit number HGG, F must equal 1. Now we know that F equals 1. Look at the answer choices; you can now eliminate answer choices D and E, and you also know that G must equal 5 or 7 (G cannot equal 6 because the problem says G must be an odd digit). When G equals 7, the product is a four-digit number; therefore, G must equal 5, and the correct answer is A. But if all that seemed too complicated, you could have just plugged the answer choices into the problem, one at a time, to see which one works. The correct answer would still be A.
15. E The variables in the answer choices should tell you that this is a great problem for Plugging In. Choose a value easily divisible by 20 (the number of friends in the group) and one for which percentages are easy to calculate (because the value of the stock increases by a percentage). For the purpose of this explanation, let’s set d equal to 100. The general fund of $100, then, was invested in Stock X, which subsequently increased in value by 40 percent; thus, its value increased to $140. At this point, the club sold the stock and divvied up the proceeds. Each member received $140 ÷ 20 = $7 in the process. Therefore, when d equals 100, the correct answer choice will yield a result of 7. Check each answer choice, plugging in 100 for d. The correct answer is E.
16. A This problem requires you to clear two hurdles. First, you must remember a rule about inscribed angles in semi-circles. Then, you must avoid succumbing to the power of suggestion. First, the rule about inscribed angles. Statement (1) tells us that QR is a diameter of the circle. That means we are dealing with two semi-circles. The question stem tells us that triangle QSR is inscribed in a circle; thus ∠QSR is inscribed. A triangle inscribed in a semi-circle is always a right triangle. Therefore, ∠QSR measures 90˚. Statement (1) is sufficient, and the correct answer must be A or D. Statement (2) can trick you if you don’t forget all about Statement (1) first. It suggests that QSR is a right triangle, because the ratio of QS to QR recall the familiar 3-4-5 triangle that satisfies the Pythagorean theorem. However, Statement (2) does not preclude the possibility that QR is not a diameter and that therefore side SR does not measure 4. There is no way to determine from this information whether QSR is a right triangle. The correct answer is A.
17. C Your old friend Joe Bloggs should help you avoid the most common mistake here; namely, choosing the answer B, 54. This answer is appealing because it makes intuitive sense; after all, if the length of a ten-stake row is 27 feet, shouldn’t the length of a twenty-stake row be twice that length? If the problem were that easy, though, this question wouldn’t be in Bin 4. Get rid of answer B. And by the way, if time is running out, before you start guessing at random, you might think about eliminating choices A and E as well. Even though 54 is clearly too easy to be the correct answer to this difficult problem, the correct answer is probably close to 54. The best way to solve this problem is to draw a diagram. Draw the first ten stakes and label the distance:

Notice that there are nine intervals between the ten stakes; each interval, then, measures exactly 3 feet (27 ÷ 3 = 9). Now look what happens when you add another ten stakes.

How many intervals are there among these 20 stakes? There are 19, each measuring exactly 3 feet. The length of the twenty-stake row, then, is 19 × 3 = 57 feet. The correct answer is C.
18. D Statement (1) tells us that the diagonal of Square H is 4 inches long. That is enough information to determine the length of a side of Square H, because the diagonal and two adjacent sides of a square form a 45-45-90 triangle, and the lengths of the sides of a 45-45-90 triangle are always in the proportion 1:1: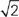 . One side of Square H has a length of
. One side of Square H has a length of 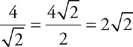 inches. The area of Square H is 8 square inches, which is indeed half the area of Square G. The correct answer must be A or D. Statement (2) mentions the diagonal of Square G, which we know to be 4
inches. The area of Square H is 8 square inches, which is indeed half the area of Square G. The correct answer must be A or D. Statement (2) mentions the diagonal of Square G, which we know to be 4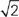 inches (the question stem tells us that the length of one side of Square G is 4 inches). Thus, the perimeter of Square H is 8
inches (the question stem tells us that the length of one side of Square G is 4 inches). Thus, the perimeter of Square H is 8 inches, and the length of one side of Square H is 2
inches, and the length of one side of Square H is 2 inches. As in Statement (1), this information is sufficient to answer the question. The correct answer is D.
inches. As in Statement (1), this information is sufficient to answer the question. The correct answer is D.
19. D You can solve this problem by drawing a Venn diagram. Because this is a problem that uses percentages without any hard numbers, you might find it easier to think of there being 100 counties. Start with all the information provided in the problem:

Because 25 percent of the counties did not receive rain on either day, 75 percent of the counties received rain on Monday, Tuesday, or both days. The sum of the number of counties that received rain on Monday and the number of counties that received rain on Tuesday is considerably greater than 75. Why? Because some counties are being counted twice. To figure out how many, subtract 75 from the sum of 70 and 65. 135 – 75 = 60, so 60 percent of the counties received rain on both days. Write the number 60 in the space where the two circles interlock. You can fill in the rest of the missing values if you like, although you do not need to do so to answer this question.

The correct answer is D.
20. C Statement (1) tells us that x – y = 7. An infinite number of combinations satisfy this equation, yielding an infinite number of perimeters for ABCD. Clearly, Statement (1) is not sufficient, and the answer must be B, C, or E. Similarly, there are many different ways to draw a rectangle with diagonal 13. Not all of these rectangles have the same perimeter. Answer choice B is also out of the mix; the answer must be C or E. At first glance, the two statements together don’t appear to offer much more help. However, by applying a bit of algebraic trickery and the Pythagorean theorem, we can wring more information from these two statements than is immediately apparent. Start by squaring Statement (1); this yields the equation x2 – 2xy + y2 = 49. The Pythagorean theorem tells us that x2 + y2 = z2, so we can use Statement (2) to substitute 132, or 169, for x2 + y2. This yields the equation 169 – 2xy = 49, which can be simplified to xy = 60. There’s just one more step. We know that x2 + y2 = 169, and we know that xy = 60. Thus, we know that x2 + 2xy + y2 = 289. The square root of x2 + 2xy + y2 is (x + y), so we also know that x + y = 17 (it cannot equal –17 because x and y are centimeter lengths). This equation, yielded by information from both statements, can be used in conjunction with Statement (1) to solve simultaneously for x and y, thus allowing you to calculate the perimeter of the rectangle. The correct answer is C. If you figured this one out on your own, have a cigar, or a bar of chocolate, or something to reward yourself. That was a mindbender!
21. B Variables in the answer choices mean it’s time to Plug In. For the purposes of this problem, it’s probably easiest to plug in weights for Andrea and Brian, add them, and use the sum for the value of p. Remember to plug in values that conform to the rules of the problem; Brian must weigh exactly 10 pounds more than Andrea. Try to make p a value that is divisible by 4; that will make it easier to calculate Cubby’s weight. For the purposes of this explanation, let’s say Andrea weighs 45 pounds and Brian weighs 55 pounds. That makes p equal to 100, a nice, round number that is easily divisible by 4. Cubby weighs  pounds more than Andrea, so he weighs 25 pounds more than Andrea, or 70 pounds. Plug 100 in for p in each of the answer choices and eliminate those that do not yield an answer of 70. The correct answer is B.
pounds more than Andrea, so he weighs 25 pounds more than Andrea, or 70 pounds. Plug 100 in for p in each of the answer choices and eliminate those that do not yield an answer of 70. The correct answer is B.
22. A This question is easier than it first appears. At first glance, the restrictive rules—the cards must be arranged in order, some cards have been removed from the deck—seem to complicate the problem. In fact, they do not; because there is only one correct solution for each set of cards chosen, you need only figure out the number of possible combinations of the cards in order to determine the number of possible correct arrangements. The one-to-one correlation between combinations and correct solutions actually simplifies the problem. Because the teacher has removed two cards from the deck, only 8 cards remain. The values on the selected cards are immaterial, and are presented merely as a distracter; the answer to this question is the same regardless of the values written on the two cards she removes. Make four spots for the cards chosen, then fill in the number of options for each spot: 8 × 7 × 6 × 5. Then, divide by the number of ways to arrange these four cards: 4 × 3 × 2 × 1. Reduce and solve to find 70. The correct answer is A.
23. E As you consider each statement, you might be tempted to think, “How many numbers can possibly satisfy all the constraints of the question stem and this statement?” Or, you may figure that both statements together, in addition to the information in the question stem, must be sufficient to answer the question. That, of course, is just what the test writers expect you to think. It turns out that several values satisfy each of the statements: 61 and 16; 72 and 27; 83 and 38; and 94 and 49 all satisfy Statements (1) and (2). Thus, neither statement is sufficient on its own, nor are they sufficient together. The correct answer is E.
24. D This is a simultaneous equation problem dressed up as a word problem. If you recognized this wolf in sheep’s clothing, you shouldn’t have had too much trouble finding the correct answer. The question stem tells us that two types of grants were awarded; it also provides the sum of the grants. Let’s call the group of freshmen who received $7,000 grants x and the group of freshmen who received $10,000 grants y. The question stem tells us that 7,000x + 10,000y = 2,300,000. That’s one equation; to solve simultaneous equations (which have two variables), we need two equations. Statement (1) provides a second equation. That equation is x + y = 275. You can solve simultaneously—although, of course, you don’t have to because this is data sufficiency, not problem solving—to determine that x = 150 and y = 125. Statement (1) is sufficient; the answer must be A or D. Statement (2) also provides a second equation. That equation is 10,000y = 7,000x + 200,000. Again, you can solve simultaneously to determine that x = 150 and y = 125. D is the correct answer to this question.
25. C When a problem includes a regular hexagon, you know a lot more than you might think. That’s because you can divide a regular hexagon into 6 congruent equilateral triangles, all meeting at the center of the hexagon. Furthermore, if you know the length of one side of an equilateral triangle, you can determine its area simply by dividing the equilateral triangle into two 30-60-90 triangles and applying the 30-60-90 formula to determine the height of the equilateral triangle (the ratio of the sides of a 30-60-90 triangle is 1 :  : 2). The problem tells you that the length of one side of the hexagon is 8 centimeters. That means that the equilateral triangles that make up the
: 2). The problem tells you that the length of one side of the hexagon is 8 centimeters. That means that the equilateral triangles that make up the
hexagon have sides of 8 centimeters. Divide one into a 30-60-90 triangle and you’ll get a triangle with sides 4 : 4 : 8; this tells you that the height of the equilateral triangle is 4
: 8; this tells you that the height of the equilateral triangle is 4 and that its area is
and that its area is  . The area of the unshaded region consists of four of the six equilateral triangles (the shaded region consists of the other two), so the area of the shaded region is 4 × 16
. The area of the unshaded region consists of four of the six equilateral triangles (the shaded region consists of the other two), so the area of the shaded region is 4 × 16 = 64
= 64 cm2. The correct answer is C.
cm2. The correct answer is C.
26. D To figure out this problem, you need to know the total number of fish. Because that total is never specified in either statement, Joe Bloggs’s first response might be to conclude there is no way to answer the question and select choice E. On the other hand, if Joe knows just a bit about probability, he might conclude the answer was choice C, because the probability that both will be Fantails is equal to the probability that the first will be a Fantail times the probability that the second will be a Fantail. However, this question wouldn’t be in Bin 4 if it were that easy. If you look at Statement (1) in combination with the question itself, you will realize that if there are 5 Fantails, and the probability that the first selection will be a Fantail is  , that means we actually know the total number of fish:
, that means we actually know the total number of fish:  =
= 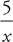 or 10. You might think that the probability of the second fish being a Fantail would also be
or 10. You might think that the probability of the second fish being a Fantail would also be  , but in fact that’s not the case: There are only 9 fish left in total when the second selection is made, and there are only 4 possible Fantails from which to chose. So the probability of them both being chosen is
, but in fact that’s not the case: There are only 9 fish left in total when the second selection is made, and there are only 4 possible Fantails from which to chose. So the probability of them both being chosen is  times
times  , or
, or  . We are down to AD.
. We are down to AD.
Now, looking at Statement (2), if the probability that the second fish will be a Fantail is  , that means that the probability of the first fish being a Fantail is
, that means that the probability of the first fish being a Fantail is  , which means we can answer the question based on Statement (2) alone as well. The correct answer is choice D.
, which means we can answer the question based on Statement (2) alone as well. The correct answer is choice D.
VERBAL BIN 1
EXPLANATIONS
1. C The pronoun they in this stem sentence doesn’t agree with the noun it refers to: the museum. In everyday speech, of course, we often say “they” when we are referring to a large institution—but on the GMAT, the test writers won’t let us get away with such imprecision. Choices A and B can both be eliminated because they use the plural pronoun. Choices D and E both fix the problem in different ways, but both add a redundancy: There is no need to have “previously” and “in the past” in the same sentence. The best answer is choice C.
2. D This is a tense question. Over the past few decades implies a continued action over time—which needs the perfect tense. This eliminates choices A and B. Choice C creates a sentence fragment. E isn’t bad, but the word since is a bit redundant because the sentence began with over the past few decades. D is best.
3. B This is an analogy argument. The men’s line is being introduced in the hope that men will like the new soft fabrics as much as women did the year before. The key word in the passage that might have alerted you to the analogy was the word same. The assumption on which this argument depends is that men and women will like the same new fabric. Choices A, C, D, and E are all outside the scope of the argument. The best answer is B.
4. B This is basically an idiom question, but your checklist may first uncover a pronoun issue. The pronoun it clearly refers back to light bulb, but in this case the pronoun isn’t actually necessary: Edison’s miraculous invention refers directly back to light bulb without the need of a pronoun. This eliminates choices A and D, both of which are actually run-on sentences. Next, you should turn your attention to the end of the underlined phrase. Do you have an invention to use energy (choices A and E), an invention that uses energy (choices B and D), or an invention using energy (choice C)? If you said that uses, then you are doing just fine. Since we’ve already eliminated choice D, the best answer is B.
5. E The clue that tells you this is a potential parallel construction problem is the word than. This sentence is supposed to compare the growth of information technology to the growth in other fields. However, as written, the sentence is comparing the growth of information technology directly to other fields. Once you spot this, you should immediately start looking for the replacement phrase, that of. Only two answer choices contain it, D and E. However, Choice D uses the awkward and unidiomatic phrase the growing of information technology. The best answer is E.
6. E This is a causal argument. According to experts, the high returns of one mutual fund cause investors to invest in other mutual funds run by the same company. However, in the case of the Grafton “family” of mutual funds, that was not the case. What conclusion can we draw from this? The best answer is E, which asks us to consider that there might be alternate causes. Choices A, B, and C are outside the scope of the argument, while D is too extreme and illogical because the argument makes it clear that investors liked at least one stock mutual fund: Grafton’s “Growth Stock Fund.”
7. A This question is about quantity words, as you probably suspected just from looking at the answer choices. When it comes to money, you use fewer if you are referring to the number of actual bills you have, but less if you are referring to the total amount and don’t know the actual number of bills. This would get you down to choices A and E. Acceptances, however, can be counted, so in the second half of the underlined portion of the underlined sentence, you would use fewer. If you were tempted by choice E, you didn’t notice that it created a new idiomatic error: Would you say as few than or as few as? The best answer is choice A.
8. D The tricky part of this inference question is dealing with the “did not.” Choice A is outside the scope of the argument because eliminating such a short commute would presumably not have much effect on productivity. Choice B is also outside the scope since the method of the commute employees would no longer have to make is probably irrelevant. If employees did not live in areas of dependable phone service, that would likely decrease productivity, so that eliminates C. For similar reasons, if employees did not have more than one phone line, it might decrease productivity since they would presumably get some personal calls at their place of residence. Choice D is best, because if employees needed to consult each other to answer callers’ questions, they would be at a distinct disadvantage if they were all in separate locations.
9. C This is a parallel construction question, in which the second half of the sentence contains a list of three actions, which must all be expressed in the same way. The three actions are breaking, stretching, and…received. Hmm. Which of the three is wrong? Well, since only received is underlined, that might be a pretty good clue that we should change it to match the others. The best answer is choice C. None of the other choices is parallel to the other two verbs. Choices B and E also add the needless pronoun it, which has no clear referent.
10. A The faulty assumption of this argument is that the buyers of the kitchen appliances are also the users of the kitchen appliances. We do not know that this is true. While more men may buy kitchen appliances, they are not necessarily the ones who use them. Choice B is wrong because knowing the individual types of kitchen appliances would not enhance the argument. Although Choices C and D might seem tempting, the problem with this argument is not so much that the survey might not be representative, but rather that the author is using information about buying patterns to extrapolate how these appliances are later going to be used and by whom. Choice E is outside the scope of the argument. The best answer is A.
11. D The GMAT test writers have an aversion to the word being, which usually creates a passive voice. This eliminates choices A and B. Generally, when a sentence begins with the infinitive verb form (To send…), you would need a parallel infinitive verb form in the second half of the sentence, which is not the case in choice C (which also uses the incorrect idiomatic expression contribution for). Choice E might seem tempting except that the last two words—as opposed—don’t go idiomatically with of. The best answer is D.
12. B Process of elimination is useful here. Does the author present a statistical analysis? No, so eliminate choice A. While the author might be said to identify the reasons for a trend, does she recommend measures to address it? No, so eliminate choice C. Does the author advocate anything whatsoever? No, so eliminate choice D. Does the author argue in favor of any policy? No, so eliminate choice E. The best answer is B.
13. B This specific question has several good lead words: Shakespeare, Cervantes, and Moliere, and they all come from the end of the second paragraph. As always, read several lines above and below the lead words to make sure you understand what’s going on. Remember, in Reading Comprehension, inference questions are not really about inferring. You are looking for an answer that restates something already said in the passage. While undoubtedly the works of these great authors are some of the most popular works of literature (choice A), how do we infer that from the passage? It was never stated. Choice C is outside the scope of this question: lawsuits are not discussed anywhere near the lead words. Choice D directly contradicts the passage. Choice E might be true but requires too big an inference for the GMAT. The best answer is B—a restatement right from the passage.
14. C A text-on-demand company would not need to acquire a book if it was already free, which leads us to choice C. Choice B might have appeared tempting, but if you read the passage, you will note that books more than 20 years old are still usually under copyright, even if in some cases it is often difficult to determine who owns the copyright.
15. D In this inference question, the trick is not to infer too far. Perhaps it could be argued that these new companies might come to supplant the publishing industry, but it isn’t said in the passage, so eliminate choice E. The same could be said for creating business plans before they have any business; it could well be true, but it isn’t said. Eliminate choice B. Choice A is not said in the passage and is illogical. Choice C is the opposite of what was stated in the passage, while choice D is a nice restatement of the passage: “looking for bargain basement content.”
16. B The key to this statistical argument is to understand that the sampling of the voters might not be representative of ALL the voters. Choice A says the voters chosen by the pollsters happened to be Democrats. But in that case, we would expect that the incumbent mayor, a Democrat, would have been predicted the winner of the election. Choice C says the exit poll was conducted at a time of day in which many people who disliked the mayor could not vote, implying that the actual election results for the incumbent would be worse, or at least no better. Choices D and E are outside the scope of the argument. The best answer is B, which gives a statistical reason for the skewed results: The exit polls were conducted in locations where the incumbent had little support—leaving open the possibility that his results would be stronger elsewhere.
17. D Although there is no “therefore” or “hence” in front of it, the bolded phrase is the conclusion of the argument. The other phrases are premises of the argument. If you suspect a phrase may be the conclusion, it sometimes helps to imagine a “therefore” in front of it, to see if the sentence would make sense. If it does, chances are that’s your conclusion. The best answer is D.
18. B The phrase not only must be followed by the phrase but also in order to complete the sentence properly. The answer must therefore be either B or C. Choice C lacks parallel structure in the words anticipate and proceeding. Correctly formulated, this sentence should read business leaders not only anticipate … but also proceed… The best answer is B.
19. C To weaken an argument, look first at its conclusion. This argument concludes that the artist will increase her profit margin … and thus increase her annual income by using cheaper art supplies. Which answer choice undercuts this conclusion? Choice C does; if the artist’s sales decrease, then her increased profit margin may not lead to an increase in annual income, because the decrease in sales may offset the increase in per-painting profit. The best answer is C.
20. E This is a pronoun agreement question. The subject of the sentence is tapirs; therefore, the pronoun that refers to the subject must be plural. The answer, therefore, must be D or E. Choice D contains a new pronoun agreement error, because they is plural and a volatile creature is singular. Choice C has no pronoun at all. The best answer is E.
21. B Because the report identifies two possible causes of the tire wear, the best answer must identify a study that focuses on one of these possible causes. Studies focusing on car models other than the Impressivo (A and D), worker satisfaction C, or driver error E are all irrelevant to this study. The study described in B removes one of the two possible causes. If the newly installed tires made by another manufacturer also turn out to wear abnormally, then the authors will have good reason to suspect that faulty alignment caused the initial problem. If the new tires wear normally, then they will know that the original tires were faulty.
22. E The author of the passage makes this point twice in the opening paragraph (the nearly forgotten Women’s Trade Union League … the WTUL made a contribution far greater than did most historical footnotes) and again in the final sentence of the passage. The entire passage serves to focus readers’ attention on “an overlooked contributor to American history,” the WTUL.
Process of Elimination is helpful here: A is incorrect because the passage is about a defunct historical union, not contemporary working women; B is incorrect because the main focus of this passage is a single organization, the WTUL; C is incorrect because the WTUL’s achievements, not its methods, are the focus of the passage; and D is incorrect because no such rebuke is ever stated. Remember also that the answer to a primary purpose question must apply to the entire passage, not just to one paragraph or section.
23. D This answer is a good paraphrase of this excerpt from the second paragraph: Because the AFL’s power stemmed from its highly skilled labor force, the organization saw little economic benefit in working with the WTUL. The affiliation provided the AFL with political cover, allowing it to claim support for women workers…
24. A This answer choice describes the AFL, not the WTUL. The passage specifically states that the WTUL represented a largely unskilled labor force [and so] had little leverage against [its] powerful opponents (lines 14–15).
25. E Process of Elimination is helpful on this question. Choice A defies common sense; if these reformers had not been sympathetic to the plight of poor women workers, they never would have joined an organization called the Women’s Trade Union League. B and C can only be justified—poorly—by “reading between the lines,” a definite no-no on reading comprehension. Because neither the reformers’ interest in Communism nor their influence within the AFL is mentioned in paragraph three (the paragraph pertinent to this question), neither answer can be correct. D is contradicted by the passage, which states that the reformers constituted a sizeable minority within the WTUL. E is a good paraphrase of this excerpt from the passage: …the reformers looked beyond the workplace, seeking state and national legislation aimed at education reform and urban poverty relief as well as workplace issues.
VERBAL BIN 2
EXPLANATIONS
1. E If you go through your mental checklist, you will probably spot the pronoun they. To whom does that pronoun refer? Even though there are a lot of plural nouns in the front half of the sentence, they must refer to the start-up company, which is singular. Never mind that many people in spoken English refer to a large company as they. On the GMAT, a singular noun needs a singular pronoun. That eliminates choices A, B, and C. To choose between D and E, look for a new error. That’s what you’ll find in choice D which uses both the words previously and in the past, creating a redundancy error. The best answer is E.
2. A In this passage, the author is questioning an analogical argument. To understand the kinetic movement of dinosaurs, says the argument, we should study the kinetic movement of birds, which are a lot like dinosaurs. The author is trying to weaken this analogy by saying that dinosaurs and birds are actually not very similar. Your job is to weaken the author’s attempt to demonstrate that the argument is flawed. How do you do that? By showing that dinosaurs and birds are in fact alike. Choice B, if anything, actually strengthens the author’s criticism of the analogy. Choices C and D are outside the scope of the argument. Choice E seems to strengthen the author’s criticism of the analogy. It is also out of scope since the fact that some bird experts don’t study dinosaurs doesn’t mean that dinosaur experts shouldn’t study birds. Choice A is best because it shows how birds and dinosaurs are alike.
3. D As always, if you don’t immediately grasp the reasoning behind an argument, scope is key to eliminating wrong answers. For example, the expense of implementing these goals (choice A) was never mentioned and thus is outside the scope of the argument. The same goes for choice B: Choosing between different types of robotic assembly lines is not part of this argument. As for choice C, the argument does not depend on whether the two actions being considered are ever actually implemented—again it is outside the scope. And, come to think of it, so is choice E, which tells us that the factory is already quite efficient; the argument is about making it more efficient. By process of elimination, you have your answer. However, here’s the logic: The conclusion of the argument is that choosing one of these two methods will result in the factory becoming the most efficient that it can be. What the argument is ignoring is the possibility that the factory could be even more efficient if it implemented both changes. The best answer is D.
4. A The idiom just as … so too is correct as written. Each of the other choices uses variations on an unidiomatic expression instead. The best answer is A.
5. B The words strongest challenge in the question mean that you are trying to weaken the argument. Choice A, if anything, appears to support the argument rather than weaken it, so you can eliminate it. Choices C and D do seem negative toward the argument, but both are outside the scope, as is choice E. Choice B is best because if the insulation comes loose after the girders arrive on site, then making an effort to prevent its dislodgement in transit to the building site will not have any effect and will not necessarily reduce fatalities.
6. A This is an idiom question. Do you attempt to do something, do you attempt at something, or do you attempt for something? Choice E uses the idiom correctly but creates a new tense error. The best answer is A.
7. C The last line of this argument gives away its type: …the virus that causes…The cause of a certain disease was thought to be one thing, but now is believed to be something else. Recent evidence suggests that the cause is a virus (which also nourishes the bacterium once thought to be the cause of the disease). To support a causal argument, you take away possible alternate causes. Choice C does this by showing that while both virus and bacterium are often present at the same time, the virus has been found without the bacterium in many cases of the disease. Choice A directly contradicts this, suggesting that the bacterium is the sole cause. B and E suggest that the virus plays a supporting role to the bacterium. D is outside the scope of the argument. The best answer is C.
8. A The second half of this sentence contains a correctly constructed parallel list. The private investor took and established, both verbs in the simple past. In choices B and D, the construction is less than parallel. In addition, several choices also use the unidiomatic established … for as opposed to established … to. In choice E, the construction is parallel, but it now seems to modify the owner and founder rather than Markham. The best answer is A.
9. B You might have been tempted by choice A, which seems to weaken the argument by saying the quality control problem of the supplier is not as severe as experts had predicted. However, the initial predictions of experts are outside the scope of the argument, because they don’t change the fact that this supplier will not be supplying any vaccines, regardless of how minor the problems might be. Similarly, what happened last year (choice C) or what will happen in the next 10 years (choice D) is also outside the scope of the argument; we want to know what will happen this year. Choice E seems to strengthen the argument since a longer flu season will presumably result in more people getting sick. The best answer is B, because if other suppliers have not been affected by quality control problems, then the overall shortage may be less severe.
10. D This question is a swirling mixture of idiom and parallel comparison. The correct idiom in question: as many … as. When you say it out loud, does so many … as seem right? Of course, it’s much easier to notice that it doesn’t when the expression has already been pulled out of the problem for you. During the GMAT, you have to do your own pulling, but remember, you always have five sensational clues: the answer choices. Even if you initially have no idea what might or might not be wrong with this sentence, you can figure it out by scanning the answers; you’ll see that you have a collection of so many as’s and as many as’s to choose from.
The other thing going on in this sentence, of course, is parallel comparison. Words such as as or than often mean a comparison is being made. The correct comparison would read: “Never before had a navy defeated as many foes at once as it defeated…,” but as you know from reading our chapter on Sentence Correction, the test writers like to see if you know that you can replace the second verb with a replacement verb: did. The best answer is D.
11. E This sentence has what should be a parallel list of nouns, beginning with an increase and a rise, but then the last two items on the list are suddenly verb-like things: depleting and raising. Since it is the last two items that are underlined, these are the items that must change. Choices A, B, and C all have verb-like things in them. Choice D, with two noun-like things, seems tempting at first, but do you say a raise of the temperature? Nope, it’s unidiomatic. Choice E is best.
12. A In this passage, the accepted practice of making thoughtful business decisions based on careful review is being questioned in light of a new theory. Both choices D and E imply that the author has rejected this new model. Choice C uses a catchy word from the passage (tenet) and fails to indicate that there is a new idea that goes against that tenet. Choice B implies that the contradiction between the theory of making decisions based on careful review and the theory of making split-second decisions has in fact been resolved. The answer is A.
13. E Where do you find the key words subconscious process? In the third paragraph. Choices A, B, C, and D are all paraphrases of examples of the processes cited in that paragraph. Only choice (E) is not. In fact, the multitude of studies and examples are cited in support of Gladwell’s hypothesis. The answer is E.
14. B Both choices A and E are too extreme to be the correct answer on the GMAT. But clearly, the new theory being described is an attempt to go beyond the conventional wisdom. The best answer is choice B.
15. D Cramer’s experiment took Evanston’s experiment even further, depriving the subjects of even more information as they tried to make a decision—and yet the subjects did nearly as well in choosing candidates. If you chose E, you got reversed: Cramer’s experiment was 8% less accurate than Evanston’s. The answer is D.
16. E This inference question asks us to go only slightly further than the passage itself—to realize that what the critics objected to was a potential tendency of the subjects to choose candidates who looked the part without really looking at their actual qualifications. If you chose C, you missed the word not in the answer choice, which turns the meaning around completely. The answer is E.
17. D The manager was apparently fired because of his team’s end-of-season statistics. If this made you wonder if the statistics were actually representative, your thinking was right on the money. To support the manager’s claim we have to show that the team’s fifth-place finish was actually better than it looked. Choices A, B, and C, while generally positive about the team (and by extension, perhaps, its manager) are outside the scope of the argument. Choice E actually puts the team’s performance in a more negative light. On the other hand, Choice D puts the team’s fifth-place finish in a very positive perspective: If the division was made up of 80 teams, finishing in fifth place is actually extremely good. The best answer is D.
18. B All of the answers to this inference question infer way too much to be the correct answer to a GMAT question—except for choice B, which simply restates a sentence from the argument itself. Choice A says an apology is needed, which is way beyond the scope of this argument. Choice C goes further than the argument to make a value judgment. Choice D looks into the future. And choice E takes a “what if” position and builds on it. The best answer is choice B.
19. E The subject of this sentence, use, is singular. Therefore, answers A, B, and C are incorrect; each states that the passengers’ use of these instruments … are prohibited. Choice D is unidiomatic, and the phrase even on the ground is unnecessarily vague. Choice E is concise, clear, and employs the correct verb. The best answer is E.
20. D Choices A, B, and C include a parallel comparison error; A and B compare classical guitars and folk guitar owners, while C compares a plural (classical guitars) and a singular (a folk guitar) noun. Choice E incorrectly suggests that the bright and brassy sound is universally preferred rather than preferred specifically by folk guitar owners. Furthermore, the placement of for their owners is unnecessarily confusing, as it separates two elements of the sentence that should be closely connected (bright and brassy sound … that only bronze and steel can create). Choice D corrects this error by setting the interceding phrase off with commas. The best answer is D.
21. B The argument presented is a causal argument. The significant underlying assumption of the argument, therefore, relates to the causal link between the anti-smoking education program and the reduction in smoking on school premises. The argument assumes that the program, and not some other set of circumstances, caused the reduction. It thus assumes that other possible causes—such as an increase in the price of cigarettes—were not substantial contributors to this result.
Process of Elimination is effective on this question, as it is on all critical reasoning questions. Because the argument hinges on one crucial piece of evidence—a decrease in the incidence of smoking on school premises—you can eliminate all answers that do not speak directly to that reduction. Thus you can eliminate A, C, and D. Choice E, if true, would weaken the argument and therefore cannot be correct. The best answer is B.
22. C Once again, your focus should be on the evidence supporting the causal link between the anti-smoking education program and the reduction in smoking on school premises. What, other than the effectiveness of the program, would explain the reduced incidence of smoking on school premises? Choice C provides a possible alternate explanation: School policy made it easier for students to leave and return to campus. It is therefore possible, then, that the reduction in smoking on school premises was simply the result of students leaving school premises to smoke, then returning afterward.
Choice B, while tempting, does not provide an alternate cause for the observed result. None of the incorrect answers addresses the evidence supporting the conclusion of the passage; therefore, none of them truly weakens the argument. The best answer is C.
23. A The sentence, as written, maintains correct parallel construction between reduce the discomfort…and result in a speedier.… Each of the incorrect answers violates the rule of parallel construction. The best answer is A.
24. D The passage describes an old problem—poverty in the developing world—and a new approach to it, that proposed by Peruvian economist Hernando de Soto. D is the best answer.
You can use Process of Elimination to get rid of all incorrect answers. Because the passage focuses on one approach and not several, its purpose cannot be to draw comparisons between two or more ideas; therefore, A and E are incorrect. The passage does not address criticism of de Soto’s plan, so neither B nor C can be correct.
25. B This answer summarizes the following information from the first paragraph: However, according to Peruvian economist Hernando de Soto, the overriding cause is the overwhelming prevalence of black market activity, well outside the formal economy, in these countries … Reforming these nations’ legal systems in order to confer ownership through titling, De Soto argues, would help the poor there access the assets their work should be generating. These assets could then be used to buy homes and build businesses, thus building a more stable and prosperous economy. The best answer is B.
26. A The key phrase in the excerpted text is wherever it is practical, which suggests that in some cases, it may be impractical to codify the existing systems. Because the purpose of codifying the existing systems is to allow developing nations to acquire market economies, it follows that where it is impractical to codify existing systems, the reason is that the systems do not meet the needs of a market economy. The best answer is A.
The incorrect answers are either unsupported by information in the passage (B, D) or directly contradicted by information in the passage
(C, E).
27. D In lines 23–24, de Soto refers to these assets as dead capital. To answer this question, we have to find out more about these assets. Earlier in the paragraph, we learn that they are the result of black market activity. The answer is D.
VERBAL BIN 3
EXPLANATIONS
1. C What can we say? You’re in Bin 3. Part of what normally makes misplaced modifiers easy to spot is that the test writers generally ask you to fix the second phrase; this time, you have to fix the first phrase. The modifying phrase Unlike F.D.R’s bootstrap program is supposed to modify the noun Ronald Reagan, which, of course, is not possible. You can’t directly compare a program to a person. We could fix the second half of the sentence (unlike F.D.R.’s program … Reagan’s program…), but since the second half of the sentence isn’t underlined, we’ll have to fix the first half. Choices B and E still directly compare F.D.R.’s program to Ronald Reagan. So does choice D. Only choice C avoids the modifier error by directly comparing F.D.R. to Reagan.
2. B The problem in the stem sentence is that there are two actions that ought to be parallel but are not. Writing (about someone else’s research) was easier than to do the research themselves. You could fix this two ways in the real world: Writing was easier than doing, or it was easier to write than to do. Each of the other answer choices mixes and matches these two ways incorrectly, except for choice B. Putting the phrase for social scientists first, as choices D and E do, would not necessarily be wrong if the verbs were parallel. Choices D and E also do not have the idiom evident that. The best answer is B.
3. D The author is arguing to nix the plan to improve the schools. We want to strengthen his argument, but before we do, there is usually at least one answer choice that actually weakens the argument. It is helpful to get rid of these first, since they are usually easier to spot. In this case, choice A gives a compelling reason to improve the school system; eliminate it. Now, the reason the author gives for defeating the plan is that the people who pay for it will not benefit. To strengthen this argument, we need to show why this would be true. Choice B is against the school improvements, but for a different reason: in other towns, similar improvements didn’t increase the quality of education. While important in the real world, this is slightly outside the scope of this argument. Choice C provides another possible negative of the plan, but again it doesn’t show why the people who pay for it will not benefit. Choice E implies that taxpayers will delay their own capital improvements to avoid paying for the schools’ capital improvements, but again this doesn’t strengthen the author’s particular argument—that the plan should be defeated because the people who must pay for it do not benefit. The best answer is D, which explains how this could be true: Most of the people slotted to pay for the school improvements don’t even have school-age children.
4. D The author says the plan is unfair to the people who must pay for it. How do we counter that? By showing that they actually do receive a benefit. Before we weaken the author’s argument, let’s eliminate any answers that strengthen it. In this case, that means only choice E. Now, choice A points out that property taxes would still be quite low even after the increase, but that doesn’t mean the increase is fair. Choice B tells us why an alternate way to finance the improvements won’t work, but doesn’t address the fairness of the way being discussed. Choice C tells us why the funds are urgently needed, but again doesn’t show that the people who have to supply the funds actually would receive a benefit. Choice D finally gives us a reason the property tax increase might actually benefit those who pay for it: Good schools translates to higher property values.
5. D As you know, GMAT test writers like to put as many words between the subject and the verb of a sentence as they can, in hopes that you will forget to check for agreement. The subject of this sentence was the plural rules. The verb: the singular includes. This eliminates choices A and B. Choices C and E are not parallel (neither is choice A), because they mix verb-like forms with noun-like forms. The best answer is D.
6. C The question here is: to what does the pronoun it refer? You might think it refers to phonetician, (in which case you might have thought the sentence was fine the way it was), but in fact it refers to the word. Choices A, B, and D could give the impression that the word is a person or persons. Choice E is awkward, and, like choice D, needlessly uses the plural people. The best answer is C.
7. A We tend to try to explain shark attacks by thinking about the shark’s behavior. But choice A points out that it takes two to tango. A shark attack requires A) one shark and B) one human to be attacked. One reason there might be fewer shark attacks on humans in cold water is that there are fewer humans swimming in cold water in the first place. If you were looking at choice B and saying, “Hmm, if a sharks’ olfactory powers were enhanced by cold water, then presumably he’d be better at attacking,” or if you were thinking that if his olfactory powers were enhanced he would know enough not to attack a human, then either way, you were having to think way too hard for this to be inside the scope. Choice C is outside the scope, too, since it is dealing with only one ocean and does not address temperature at all. Choice D provides extraneous information, and choice E does not help to explain the apparent paradox. The best answer is A.
8. D The sentence, as written, needs a but also to complement its not only. Choices A and E bite the dust. In choice B, the same idiom comes into play, but this choice has bigger problems: Without the who warned, it is no longer clear who is doing the warning. Choice C can be eliminated for the same reason. The best answer is D.
9. B To weaken a causal argument, propose an alternate cause. To strengthen a causal argument, remove an alternate cause. Choice A weakens the argument, so cross that off. Choices C and D both appear to strengthen the case for global warming in general, but do not make the important connection between the warming of the waters of the Caribbean and global warming in general. Choice E promises that the mechanism that creates more severe storms will soon be better understood, but that doesn’t help to make the case that the warm water causing more severe hurricanes is related to global warming. The best answer is B. While choice B might seem unlikely, it strengthens this causal argument by removing a possible alternate cause. If there were an undersea volcano heating the Caribbean, then that might be what was causing the severe hurricanes, not global warming.
10. C The key word here is than—and if you spotted it, you knew to look for a parallel comparison problem. Two actions are being compared in this sentence, so we need the words “it was” after than to make that clear. If you spotted this error, you could eliminate Choices A, B, and E. D might seem possible (and parallel in a different kind of way) until you get to the last words: 10 years in the past. This is just not the same as ago. The best answer is C.
11. C This passage presents an overview of the legal issues involved in age discrimination. Choices A and E are wrong because they imply that the passage takes sides on the matter. B is tempting, but the passage doesn’t discuss the origins of the issues. Choice D implies that the passage is describing the aging process itself. The answer is C.
12. D The contradiction highlighted at the beginning of the second paragraph is not resolved or qualified; it is stated, and then its ramifications are outlined. The answer is D.
13. C To weaken the assertion that it might be in the interest of employers to fire older people, it is necessary to show why employing older people would be GOOD for companies. C is the only answer that does so, suggesting that older employees are actually more productive and have fewer health care costs.
14. B The trick in any inference question is not to infer too far. Many of the possible answers here might well be inferred in a normal interchange, but on the GMAT, the best answer will generally seem almost laughably self-evident. In this case, that is B. Choices A and C are much too cynical to be correct answers on the GMAT, and choices D and E go well beyond the scope of the question.
15. A All of these costs were cited with one exception: the cost of out-placement services. The answer is A.
16. A The drug company says its drug caused enhanced learning ability. To weaken this causal argument, look for an alternate cause. Choices B, D, and E appear to strengthen the argument, so we can eliminate them. Choice C, while clearly a negative aspect of the drug, does not weaken the argument itself, which states simply that the drug enhances learning capability in children. Side effects are outside the scope of the argument. Choice A may not seem at first like an alternate cause, but if the control group (which did not receive the medicine) reported the exact same results as the children who did receive the drug, then clearly there is some other, as yet unnamed, alternate cause. The best answer is A.
17. E To evaluate the significance of the author’s claims, we need to recognize what kind of argument it is: an analogy. The author is saying that the situation in Country Y is analogous to that of Country Z. To weaken an analogy, you merely have to question whether the two situations were really analogous. Choices A and B are outside the scope of the argument. Choice C is incorrect because the author’s argument stated that more-stringent laws were needed, making it irrelevant whether Country Y had any laws about this in the first place. Choice D goes off on an interesting tangent by asking if there were business ties between the two countries, but it does not weaken the argument’s analogy. Only choice E questions whether the two situations are in fact analogous. E is the best answer.
18. B This question tests two concepts. The first is idiomatic and concerns the word require. Because the word require indicates something that is compulsory (as opposed to optional), it cannot be followed by the word should; in other words, you can’t require that something should happen, because then it’s not really a requirement. This eliminates A and C.
The second concept is a little more arcane. Requirements, like hypothetical situations posited in the future, take the subjunctive mood. In the subjunctive, the proper way to phrase the idea expressed in this sentence is the rules require that applicants be physically fit. Tough and obscure, but that’s why this question is in Bin 3. If you get this question wrong, suck it up and move on, confident in the knowledge that you can miss this one and still score a 790.
19. C This question presents two ways to discuss the unfortunate toad incident on the Outer Banks. Was there a massive toad infestation or a massive infestation of toads? The second option is better, because the first leaves it unclear whether massive refers to the infestation or the toads themselves. Under the first option, it is theoretically possible that the Outer Banks was infested by a single 50-foot-tall toad. Thus, A, B, and E are all incorrect. Choice D incorrectly suggests that the Outer Banks, not the infestation of toads, discouraged vacationers.
20. E During a period of robust home sales, one would expect the prices of all homes to increase; that would be the natural effect of the law of supply and demand. The question tells us, however, that the real price of resale homes during this period actually decreased. Thus, it is reasonable to assume that the demand for resale homes decreased. How can we resolve this apparent contradiction? If all the increased demand for homes was in the new home market, then it would be possible that the overall increase in home sales would not result in an increase in resale home prices and may, in fact, even accompany a drop in those prices. The best answer is E.
21. B This question is best solved by drawing a diagram to represent the information in the question stem.

We are looking for information that will allow us to draw the diagram

According to the question stem, four of the answer choices are sufficient to accomplish this. Your job is to find the one that is NOT sufficient.
Choice A is sufficient; if Kiko is taller than Luis and Luis is taller than Rei, Kiko must be taller than Rei.
Choice B is NOT sufficient; if Luis is taller than Marcus, then it is conceivable that Luis is taller than Kiko. Consequently, it is also possible that Rei, who is shorter than Luis, is also taller than Kiko; however, Rei may also be shorter. The best answer is B.
Use the diagrams we have already created to demonstrate, on your own, that C, D, and E are sufficient to make the conclusion logically sound.
22. A Well, you’ve got five choices here and none is particularly good. Only four, however, contain grammatical errors, so the best way to proceed on a question like this one is to eliminate as many answer choices as you can, take your best guess from among the remaining answers, and move on. Choice B is an endless string of prepositions; furthermore, the placement of the phrase of the region between increase in the average temperature and of even 0.5 degrees Fahrenheit is needlessly confusing. Choice C incorrectly suggests that it is agriculture, and not lost income, that results from the temperature increase. In D, cost from is unidiomatic; the correct phrasing is cost of. Choice E is redundant, as it refers to annual losses that occur each year. The best answer is A.
23. D This is a tricky between/among question. The rule is that between is used to compare two items, among to compare three or more. Here we are talking about thousands of people, so you might think that among is the correct choice. However, because the sentence compares two groups of people, the correct answer is between. The argument is between the two groups, not among the thousands of people who make up those groups. Eliminate A and B.
We can eliminate C because it is unidiomatic: It draws a comparison between one group with another when it should draw a comparison between one group and another. Choice E can be eliminated because it lacks parallel structure: It compares those believing that achieving some goals… and those who believe that the principles of the party must not be abandoned. The best answer is D.
24. D Answer D may explain why people are more likely to exceed the speed limit in Oak Valley than in Mountainview, but it has no necessary correlation to the number of accidents in the two towns; therefore, it does nothing to weaken the conclusion that the greater proportion of speeders in Oak Valley results in a greater number of accidents there.
Answers A and E provide an alternate explanation: Driving conditions are poor, which certainly could contribute to accidents. Choice B indicates that there is much more traffic in Oak Valley, which could well explain why there are more traffic accidents there. Choice C states that many Mountainview residents travel to Oak Valley regularly; it is possible, then, that they, not the drivers who live in Oak Valley, cause the accidents.
25. B The statement draws a conclusion about people who train their dogs based on statistics relating only to people who take their dogs for formal obedience training classes. In order for the statement to be correct, then, these statistics must be valid for all people who train their dogs, not only those who train them in formal classes. Choice B plugs this hole in the argument, thus making the conclusion necessarily true.
26. C To answer this parallel-the-reasoning question, you have to break down the original argument, and then find an answer choice that mimics it exactly. In this case, the argument says a bullet train travels in excess of 150 miles per hour (if A, then B). Therefore, if a train travels less than 150 miles per hour, then it is not a bullet train (if not B, then not A). Now all you have to do is find an answer choice that mimics that reasoning exactly. Choice A, broken down, reads, “if A, then B … so if B, then not A.” This isn’t it. Eliminate it. Choice B breaks down to “if A, then B … therefore C will also cause B.” That’s not it either. Choice C breaks down to “if A, then B … therefore if not B, then not A.” This is the best answer.
Choice D might seem tempting because it also has to do with a fast means of transportation, but what counts here is the reasoning: if A, then B … if not A, then not B. This is close, but no cigar. Choice E is also appealing; you may even think it mimics the argument exactly. But there’s a trick. The first half of the sentence reads, “Fluoride generally prevents cavities” (if A then B). Note that the B part is about the prevention—not the presence—of cavities. So the second half, “If there are no cavities, there was no fluoride,” actually breaks down to “if B, then not A.”
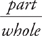 . In this case,
. In this case, 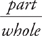 =
= 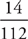 =
=  ; cross-multiply to get 112x = 1,400, so x =
; cross-multiply to get 112x = 1,400, so x =  , and x = 12.5.
, and x = 12.5.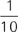 , or 10%, of 112—11.2 is exactly 10%—so the answer can only be C.
, or 10%, of 112—11.2 is exactly 10%—so the answer can only be C. , and Company A had 24,000 employees; that 20% at Company B is the same as
, and Company A had 24,000 employees; that 20% at Company B is the same as  , and Company B had 12,500 employees. The answer to the original question is “no”; Company A did not have more than twice the number of employees as did Company B.)
, and Company B had 12,500 employees. The answer to the original question is “no”; Company A did not have more than twice the number of employees as did Company B.)
 =
=  =
=  = 13. For the smaller rectangular solid,
= 13. For the smaller rectangular solid,  =
= 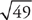 = 7. Both 13 and 7 are, of course, answer choices, but the problem asked us for the difference between the two values, so the correct answer is 6, choice B.
= 7. Both 13 and 7 are, of course, answer choices, but the problem asked us for the difference between the two values, so the correct answer is 6, choice B. = 8. To simplify this equation, multiply both sides by 3 to get a + b + c = 24. If the sum is 24, then the average is 8.
= 8. To simplify this equation, multiply both sides by 3 to get a + b + c = 24. If the sum is 24, then the average is 8. to get
to get 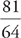 . Those are both perfect squares, so the inner root sign will be easy to handle:
. Those are both perfect squares, so the inner root sign will be easy to handle: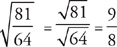 . Don’t grab answer choice C, though—we still need to work the outer sign:
. Don’t grab answer choice C, though—we still need to work the outer sign: . Like in high school, we can’t leave a radical on the bottom of a fraction, so we’ll need to multiply our answer by
. Like in high school, we can’t leave a radical on the bottom of a fraction, so we’ll need to multiply our answer by 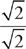 to get our final answer of B,
to get our final answer of B, 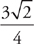 .
. is a little greater than 1; the square root of something a little greater than 1 is also something a little greater than 1; and the square root of that number is, again, something a little greater than 1. Only B and C are a little greater than 1.
is a little greater than 1; the square root of something a little greater than 1 is also something a little greater than 1; and the square root of that number is, again, something a little greater than 1. Only B and C are a little greater than 1.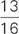 full to
full to  full; that’s a difference of
full; that’s a difference of  , or
, or  , so we know that 1,250 represents
, so we know that 1,250 represents  of the total seating capacity of the stadium. The stadium must, therefore, hold 8 × 1,250, or 10,000 people, and we’re down to A or D.
of the total seating capacity of the stadium. The stadium must, therefore, hold 8 × 1,250, or 10,000 people, and we’re down to A or D.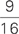 and
and 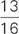 , that is,
, that is,  , or
, or  of the stadium’s total seating capacity. So we know we can find the total seating capacity (4 × 2,500, or 10,000 people) with Statement (2) as well, making D the correct answer.
of the stadium’s total seating capacity. So we know we can find the total seating capacity (4 × 2,500, or 10,000 people) with Statement (2) as well, making D the correct answer. of that, or $15, he currently has $20 left to save. Before the end of the summer he’ll be able to save
of that, or $15, he currently has $20 left to save. Before the end of the summer he’ll be able to save  of that remaining $20, or $8. That will give him a total of $23 saved toward his car, leaving him $12 to go. Expressed as a fraction of the cost of the car, that’s
of that remaining $20, or $8. That will give him a total of $23 saved toward his car, leaving him $12 to go. Expressed as a fraction of the cost of the car, that’s  , and the correct answer is C.
, and the correct answer is C.

 the list price of the Touristo. The list price of the Touristo is therefore greater than the list price of the Leisure. Statement (1) is sufficient; the answer must be A or D. Statement (2) tells you that the list price of the Touristo is 1.2 times the list price of the Leisure. So Statement (2) also tells you that the list price of the Touristo is greater than the list price of the Leisure. The correct answer is D.
the list price of the Touristo. The list price of the Touristo is therefore greater than the list price of the Leisure. Statement (1) is sufficient; the answer must be A or D. Statement (2) tells you that the list price of the Touristo is 1.2 times the list price of the Leisure. So Statement (2) also tells you that the list price of the Touristo is greater than the list price of the Leisure. The correct answer is D. , or 0.0025. Either way, when you multiply by 600, the result is 1.5. The quotient is thus 1.5 divided by 150, or 0.01. The answer is D.
, or 0.0025. Either way, when you multiply by 600, the result is 1.5. The quotient is thus 1.5 divided by 150, or 0.01. The answer is D. , which easily cancels down to
, which easily cancels down to  , or 0.01.
, or 0.01. , so x =
, so x =  , or
, or  …or
…or  =
= 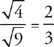 . The correct answer is C. Answer choice B, of course, is x itself, and answer choice D is
. The correct answer is C. Answer choice B, of course, is x itself, and answer choice D is  .
. , to be exact). Close, but not quite. We need fewer laps to bring down Steven’s average speed, so answer choice B is the next logical choice. Five laps in 51 seconds means Steven has driven 5 × 51, or 255, seconds so far, and the additional 39-second lap gives us a total of 6 laps driven in 294 seconds. The average is now
, to be exact). Close, but not quite. We need fewer laps to bring down Steven’s average speed, so answer choice B is the next logical choice. Five laps in 51 seconds means Steven has driven 5 × 51, or 255, seconds so far, and the additional 39-second lap gives us a total of 6 laps driven in 294 seconds. The average is now  = 49 seconds, and B is the correct answer.
= 49 seconds, and B is the correct answer. = 13. Now plug 2 in for x in the answer choices—only answer choice A gives us 13, so it must be the correct answer.
= 13. Now plug 2 in for x in the answer choices—only answer choice A gives us 13, so it must be the correct answer. , this question is just a matter of putting the four values in order. Even better, you already know two of them: x = –
, this question is just a matter of putting the four values in order. Even better, you already know two of them: x = – , as it will always be if we meet the requirements of Statement (2) and the question itself.
, as it will always be if we meet the requirements of Statement (2) and the question itself. =
=  ,
,  =
=  . Now plug the value of y into the equation:
. Now plug the value of y into the equation:
 = 0; since the numerator must be zero in order for the fraction itself to equal zero, we know that a + c = 0. Subtract a from both sides and c = –a. The answer is A.
= 0; since the numerator must be zero in order for the fraction itself to equal zero, we know that a + c = 0. Subtract a from both sides and c = –a. The answer is A. . Now we just have to figure out how many of those possibilities meet the requirement.
. Now we just have to figure out how many of those possibilities meet the requirement. , or
, or  since we know from the question that p is an integer, the answer to the question is “yes,” and our answer is B. Of course, we can easily show the sufficiency of Statement (2) by plugging in values for p and q: as long as the values are equal integers, our answer is always “yes.”
since we know from the question that p is an integer, the answer to the question is “yes,” and our answer is B. Of course, we can easily show the sufficiency of Statement (2) by plugging in values for p and q: as long as the values are equal integers, our answer is always “yes.” . The probability that Jessica will be chosen is also
. The probability that Jessica will be chosen is also 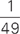 . This happens to be choice A, but we aren’t done yet. The question asks for the probability that they will NOT both be chosen. The probability that an event does NOT happen can be expressed as 1 minus the probability that the event DOES happen. So 1 minus
. This happens to be choice A, but we aren’t done yet. The question asks for the probability that they will NOT both be chosen. The probability that an event does NOT happen can be expressed as 1 minus the probability that the event DOES happen. So 1 minus  , or choice E.
, or choice E. . The probability that the second roll will yield the number 6 is also
. The probability that the second roll will yield the number 6 is also 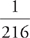 . That’s choice A, but we aren’t done yet.
. That’s choice A, but we aren’t done yet.  . The correct answer is choice E.
. The correct answer is choice E. (B + 10). Thus, between the question stem and Statement (1), we have two non-identical equations, which means we can solve for our two variables. (Best of all, because this is a data sufficiency question, just knowing this is enough; we don’t have to actually solve it!) Rule out B, C, and E.
(B + 10). Thus, between the question stem and Statement (1), we have two non-identical equations, which means we can solve for our two variables. (Best of all, because this is a data sufficiency question, just knowing this is enough; we don’t have to actually solve it!) Rule out B, C, and E. a. Convert the fraction to a decimal by dividing 35 by 20 to yield b = 1.75a. The correct answer is D.
a. Convert the fraction to a decimal by dividing 35 by 20 to yield b = 1.75a. The correct answer is D. . If this is the correct answer, then the ratio of (42 + 4) to 63 would be 3 to 4. It is not, so this answer must be incorrect.
. If this is the correct answer, then the ratio of (42 + 4) to 63 would be 3 to 4. It is not, so this answer must be incorrect. is an integer. Wait a minute, though: w could also equal 13, because 13 + 3 = 4s is also solvable. Because
is an integer. Wait a minute, though: w could also equal 13, because 13 + 3 = 4s is also solvable. Because  is not an integer, Statement (2) is not sufficient. Sometimes it answers “yes,” other times it answers “no.” Eliminate B.
is not an integer, Statement (2) is not sufficient. Sometimes it answers “yes,” other times it answers “no.” Eliminate B.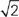 is enough to tell us that the short sides are both 8. Once we know the radius, we can solve for the area—64π, if you were wondering—and we’re down to A or D.
is enough to tell us that the short sides are both 8. Once we know the radius, we can solve for the area—64π, if you were wondering—and we’re down to A or D. , or
, or 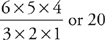
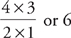
 = 3 + 10 = 13 animals. The correct answer is C.
= 3 + 10 = 13 animals. The correct answer is C.

 when P = 18. Finally, simply plug in 18 for P in every answer choice and eliminate those that do not yield a result of 3
when P = 18. Finally, simply plug in 18 for P in every answer choice and eliminate those that do not yield a result of 3 . Therefore, if we know the ratio of the bases and the heights of these triangles, it would be safe to assume that we know enough to calculate the ratios of their areas. This makes C a very tempting answer, because Statement (1) provides the ratio of the heights of the two triangles and Statement (2) provides the ratio of the bases of the two triangles. Well, now, if it were that easy, it wouldn’t be in Bin 3, would it?
. Therefore, if we know the ratio of the bases and the heights of these triangles, it would be safe to assume that we know enough to calculate the ratios of their areas. This makes C a very tempting answer, because Statement (1) provides the ratio of the heights of the two triangles and Statement (2) provides the ratio of the bases of the two triangles. Well, now, if it were that easy, it wouldn’t be in Bin 3, would it? , which reduces to
, which reduces to  . The correct answer is C.
. The correct answer is C.



 , or 12,000, were sold. The question asks what fraction of the unsold seats in the stadium were in the lower deck. Because 40,000 seats were sold in the entire stadium, a total of 20,000 were unsold; of the 20,000 unsold seats, 15,000 – 12,000 = 3,000 were in the lower deck. The fraction
, or 12,000, were sold. The question asks what fraction of the unsold seats in the stadium were in the lower deck. Because 40,000 seats were sold in the entire stadium, a total of 20,000 were unsold; of the 20,000 unsold seats, 15,000 – 12,000 = 3,000 were in the lower deck. The fraction  reduces to
reduces to 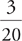 , so the correct answer is A.
, so the correct answer is A. = 38. The average age of 30 executives and 120 non-executives is
= 38. The average age of 30 executives and 120 non-executives is  = 38. Thus, the correct answer is B. Joe Bloggs, by the way, picks C on this problem.
= 38. Thus, the correct answer is B. Joe Bloggs, by the way, picks C on this problem.

 inches. The area of Square H is 8 square inches, which is indeed half the area of Square G. The correct answer must be A or D. Statement (2) mentions the diagonal of Square G, which we know to be 4
inches. The area of Square H is 8 square inches, which is indeed half the area of Square G. The correct answer must be A or D. Statement (2) mentions the diagonal of Square G, which we know to be 4

 pounds more than Andrea, so he weighs 25 pounds more than Andrea, or 70 pounds. Plug 100 in for p in each of the answer choices and eliminate those that do not yield an answer of 70. The correct answer is B.
pounds more than Andrea, so he weighs 25 pounds more than Andrea, or 70 pounds. Plug 100 in for p in each of the answer choices and eliminate those that do not yield an answer of 70. The correct answer is B. . The area of the unshaded region consists of four of the six equilateral triangles (the shaded region consists of the other two), so the area of the shaded region is 4 × 16
. The area of the unshaded region consists of four of the six equilateral triangles (the shaded region consists of the other two), so the area of the shaded region is 4 × 16 or 10. You might think that the probability of the second fish being a Fantail would also be
or 10. You might think that the probability of the second fish being a Fantail would also be  , or
, or  . We are down to AD.
. We are down to AD. , which means we can answer the question based on Statement (2) alone as well. The correct answer is choice D.
, which means we can answer the question based on Statement (2) alone as well. The correct answer is choice D.

