Unpredictability

Create a sketch for a coin that is “tossed” every time the mouse button is clicked. Your coin should be evenly weighted so that heads and tails have the same likelihood of appearing. Test your program over ten tosses. What were the observed frequencies of heads and tails?

Create an app in which a virtual die is “rolled” every time the mouse is clicked. Your die should be evenly weighted, and each result should have an even 1-in-6 chance of appearing. Test your program over 18 clicks. How well does it perform? Modify your code so that it rolls six dice.
Ask some friends to prepare drawings of heads, torsos, and legs. Make sure these parts are able to line up interchangeably at the neck and waist. Create an “Exquisite Corpse” generator in which these parts are randomly recombined whenever a button is clicked. (Image: Tatyana Mustakos)
Create a time-based sketch in which a brief event (such as a sound or animation) is triggered sporadically and unpredictably, with a very low probability. You may also display a scrolling timeline showing a history of when the event occurred.

Make an interactive composition that depicts “order” when the cursor is on the left side of the canvas, and “chaos” when it is on the right. The amount of order or chaos (entropy) should vary smoothly according to the cursor position. The map() and constrain() functions may be helpful.
Create a sketch in which a small 2D element travels erratically from one moment to the next, leaving a trail across the canvas as it moves. At every timestep, it should update its current position with a small random displacement in both X and Y.

Drunk Walk II: Random Lattice Walk
Create a sketch in which a small element travels erratically from one moment to the next, leaving a trail as it moves. At every timestep, it should have a 1-in-4 chance of moving up, down, left, or right from its previous position.

Drunk Walk III: Smoothed Noise
The smoothed quality of Perlin noise allows you to make an animation that is unpredictable, but also has temporal coherence. Use Perlin noise to dynamically regulate the size and position of a circle. Observe the effects of changing the parameters to the noise function.

In each cell of a square grid, choose with random probability to place a diagonal line pointing up or down. The fascinating maze-like patterns that arise are discussed at length in the book 10 PRINT CHR$(205.5+RND(1)); : GOTO 10 by Nick Montfort et al.1

Create a set of four duotone “Truchet tiles,” each with two quarter-circles connecting the midpoints of adjacent sides. Be sure to create all possible orientations and all possible colorings (corners light or corners dark). Randomly place these tiles in a square grid, enforcing continuity of color.
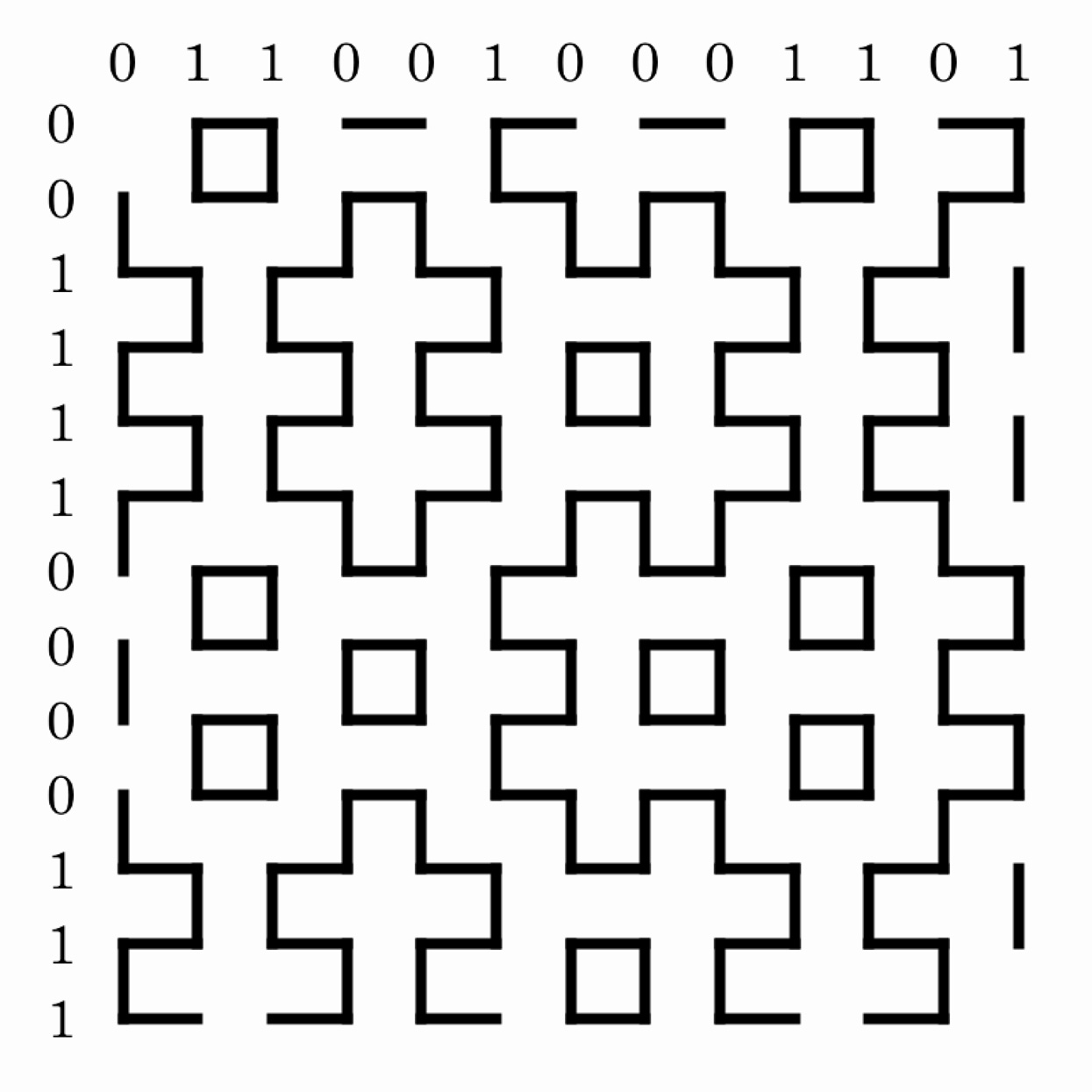
Randomly label the columns and rows of a grid with 0s and 1s. For each column, draw a vertical sequence of alternating dashes and gaps, beginning with a dash (for columns labeled 1) or a gap (for columns labeled 0). Similarly, draw horizontal sequences of dashes and gaps for the rows. Observe the resulting patterns.2

Generate some mountains by creating a series of parallel lines with no spacing between them, spanning from the bottom of the screen to an unpredicable height. Use a Perlin noise function to determine the height of each line.
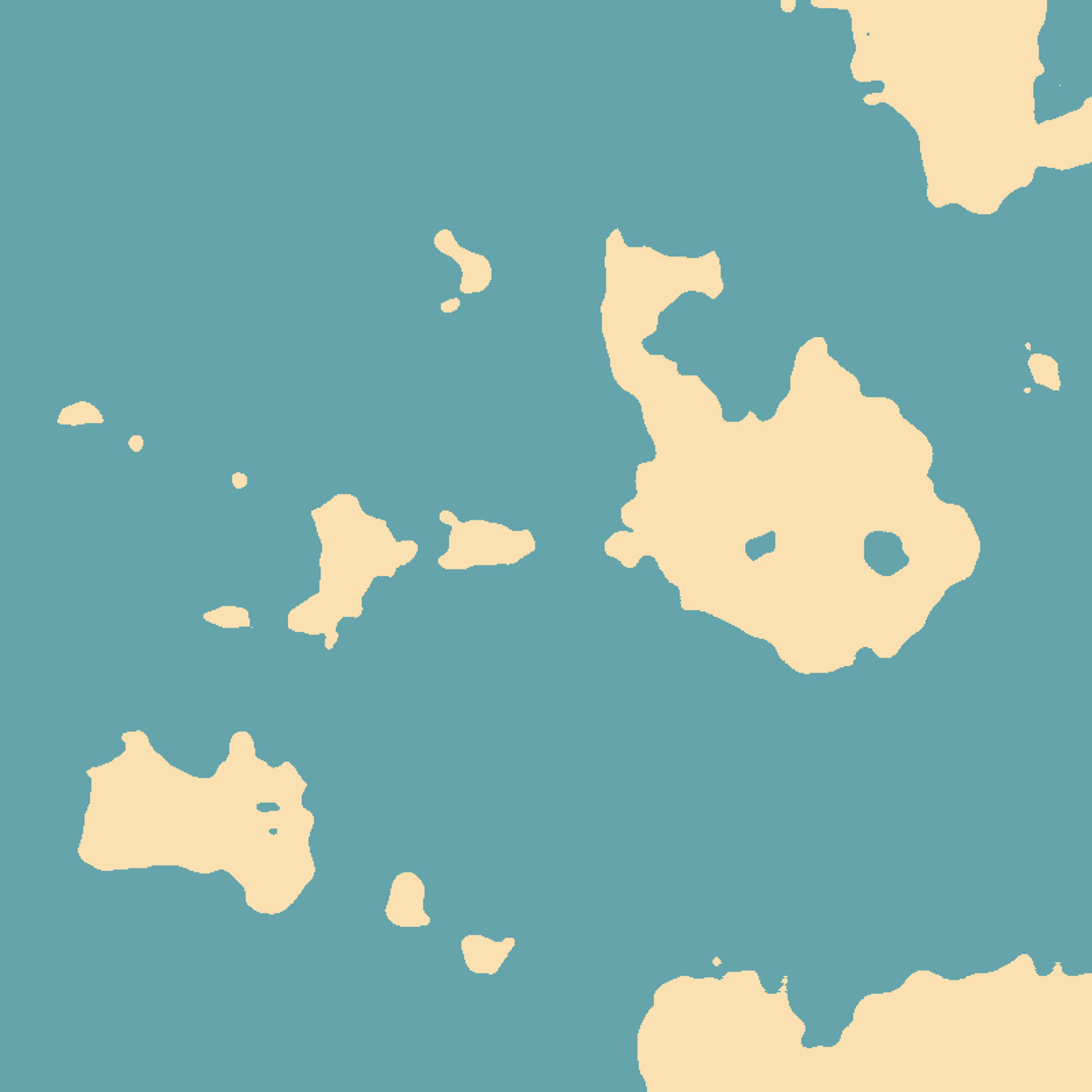
Use a two-dimensional Perlin noise function to generate a map of imaginary islands. For every pixel: if the value of the noise function is below some threshold value, color the pixel blue (for water); if it is higher than the threshold, color it brown (for land).

Recoding Molnár's Interruptions
Carefully study some reproductions of the computational plotter work Interruptions (1968–1969) by Vera Molnár.3 Note how it consists of a grid of lines whose orientations have been randomized. Some lines are also missing, in patches. Write down ten additional observations about the work. To the best of your abilities, write a program to “re-code” Interruptions. Write a few sentences describing how your version succeeds or falls short.