Geometry
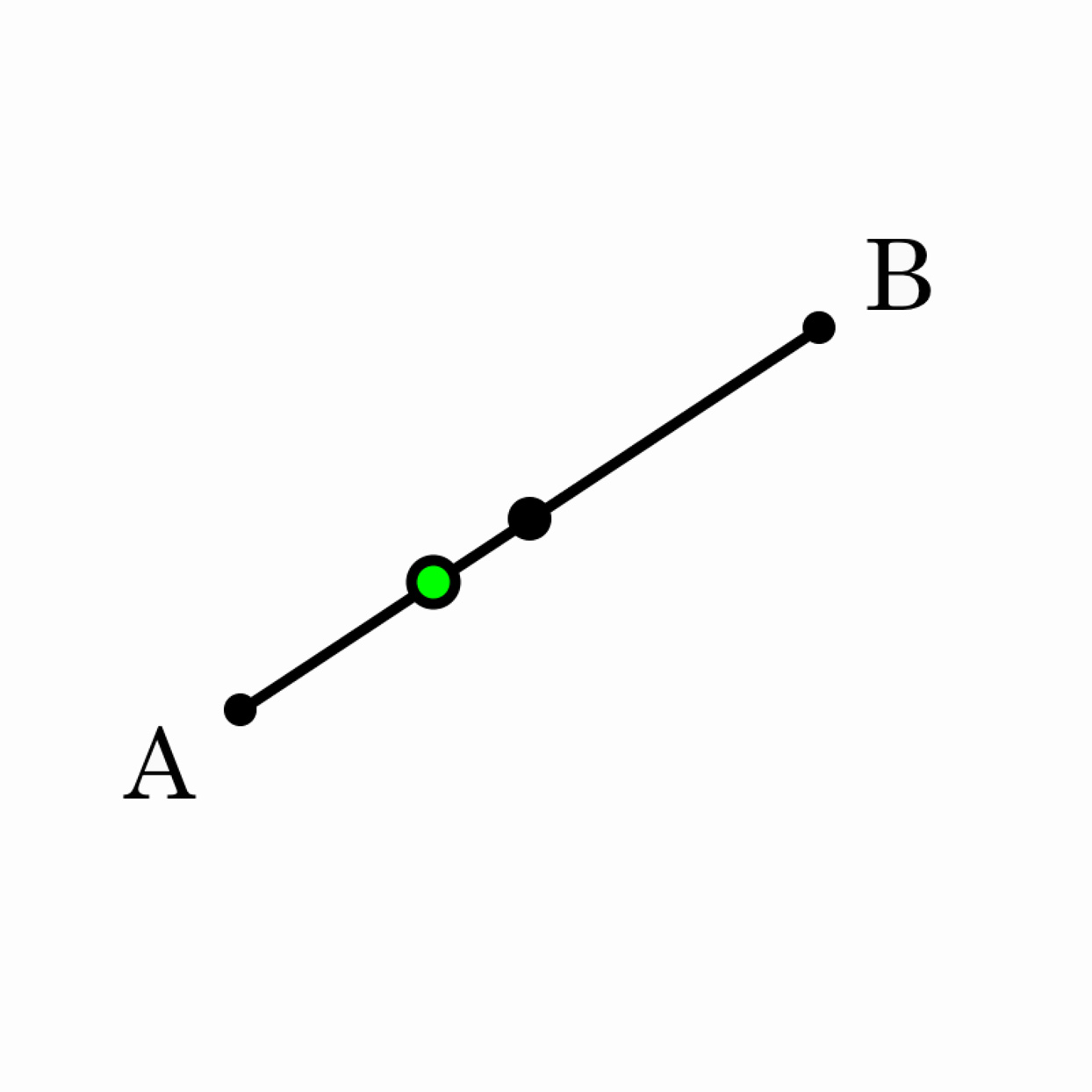
Write a program that draws two random points (A and B) whenever a button is pressed. Connect these points with a line segment. Calculate the midpoint of this line segment, and place a dot there. Place an additional circle one-third of the way from A to B.
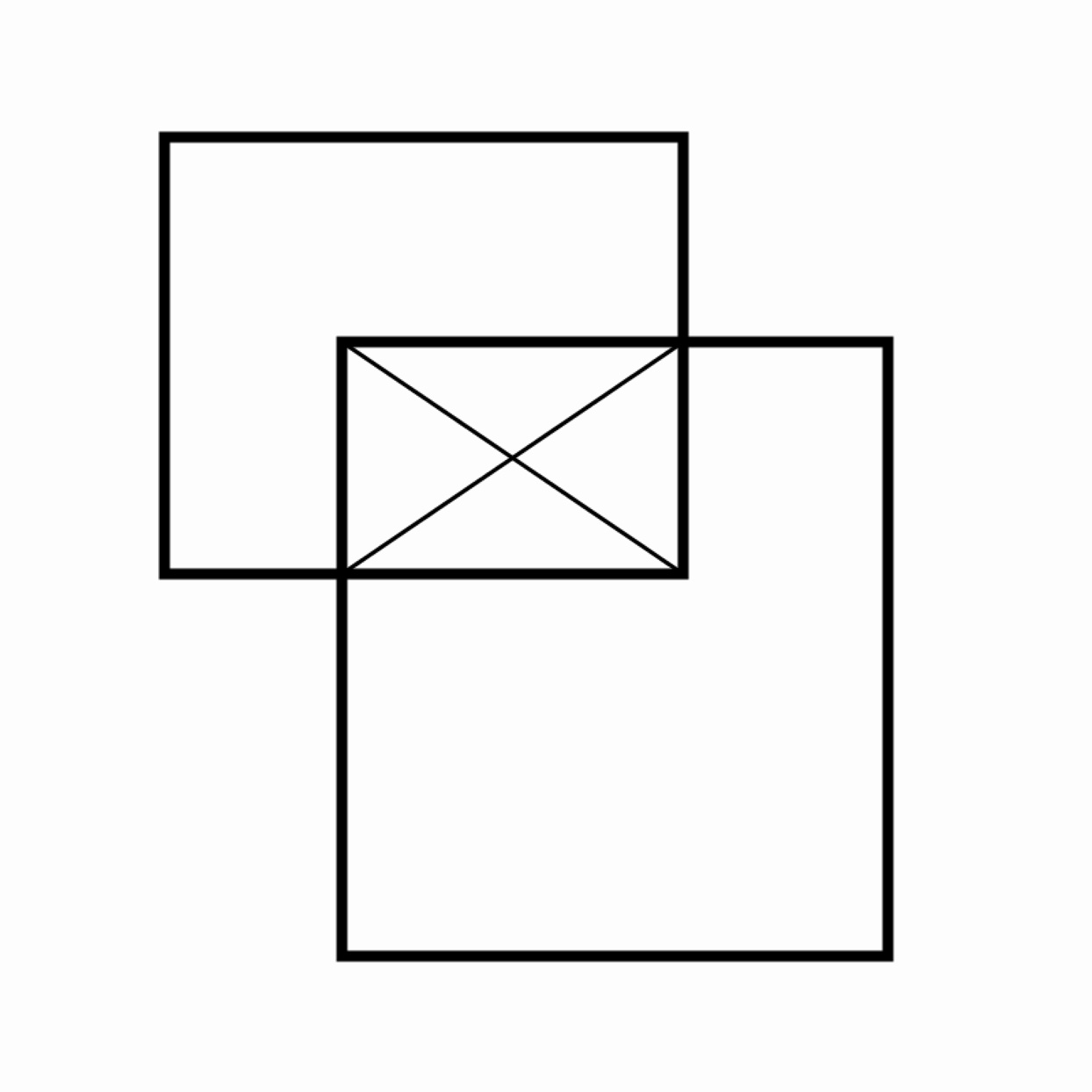
Intersection of Two Rectangles
Write a program that draws two randomly sized, randomly placed rectangles whenever a button is pressed. If these rectangles overlap, locate the new rectangle that represents their overlapping region and draw its diagonals.
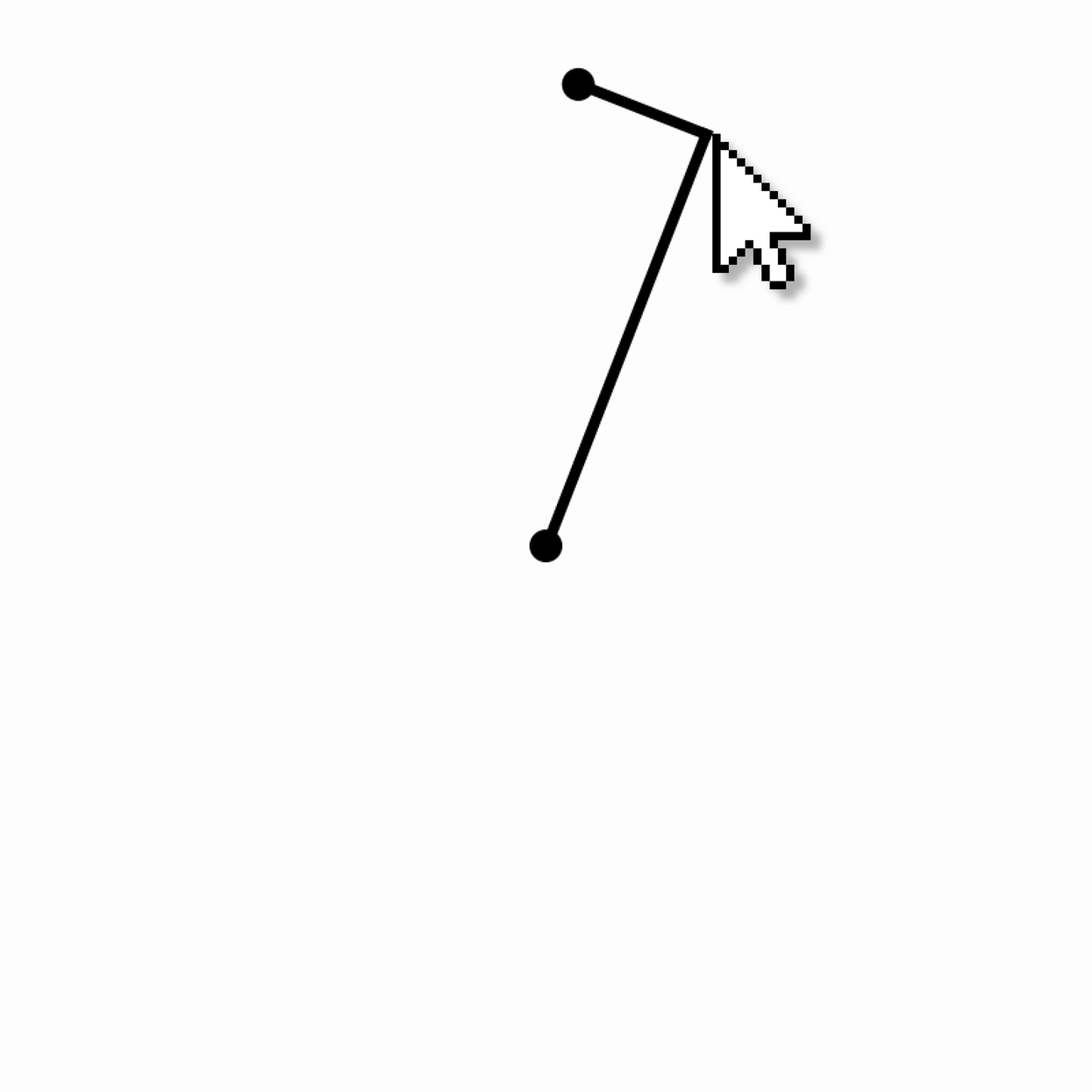
Construction of a Perpendicular
Write a program that draws a line from the center of the canvas to the cursor. Construct a second line that starts at the cursor, is 50 pixels long, and is perpendicular to the first line.
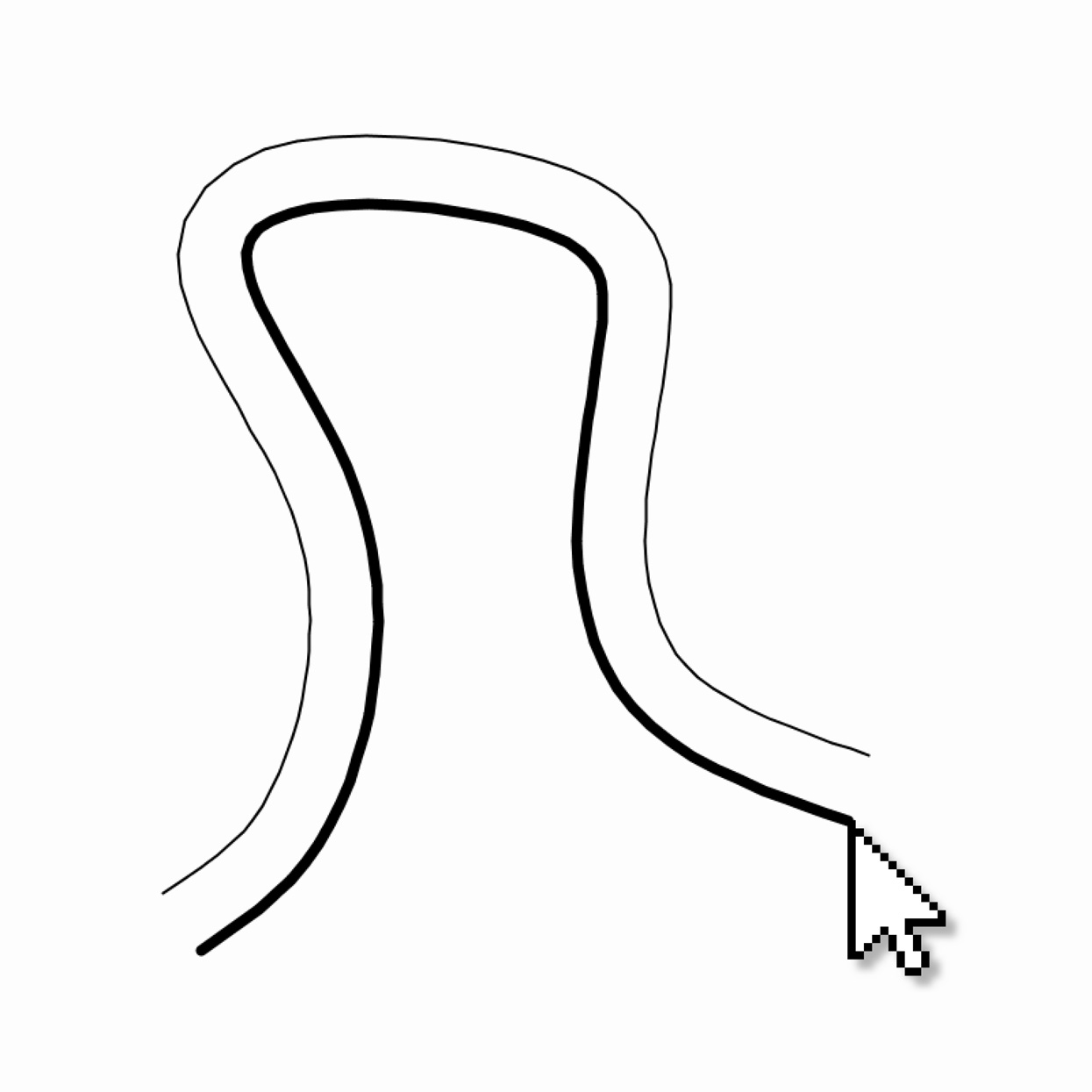
Parallel Polyline (Offset Curve)
Write a program that stores cursor points as a user draws. Connect these points with a polyline. Use geometry to calculate another polyline, which is offset everywhere from the user's drawing by a distance of 50 pixels.
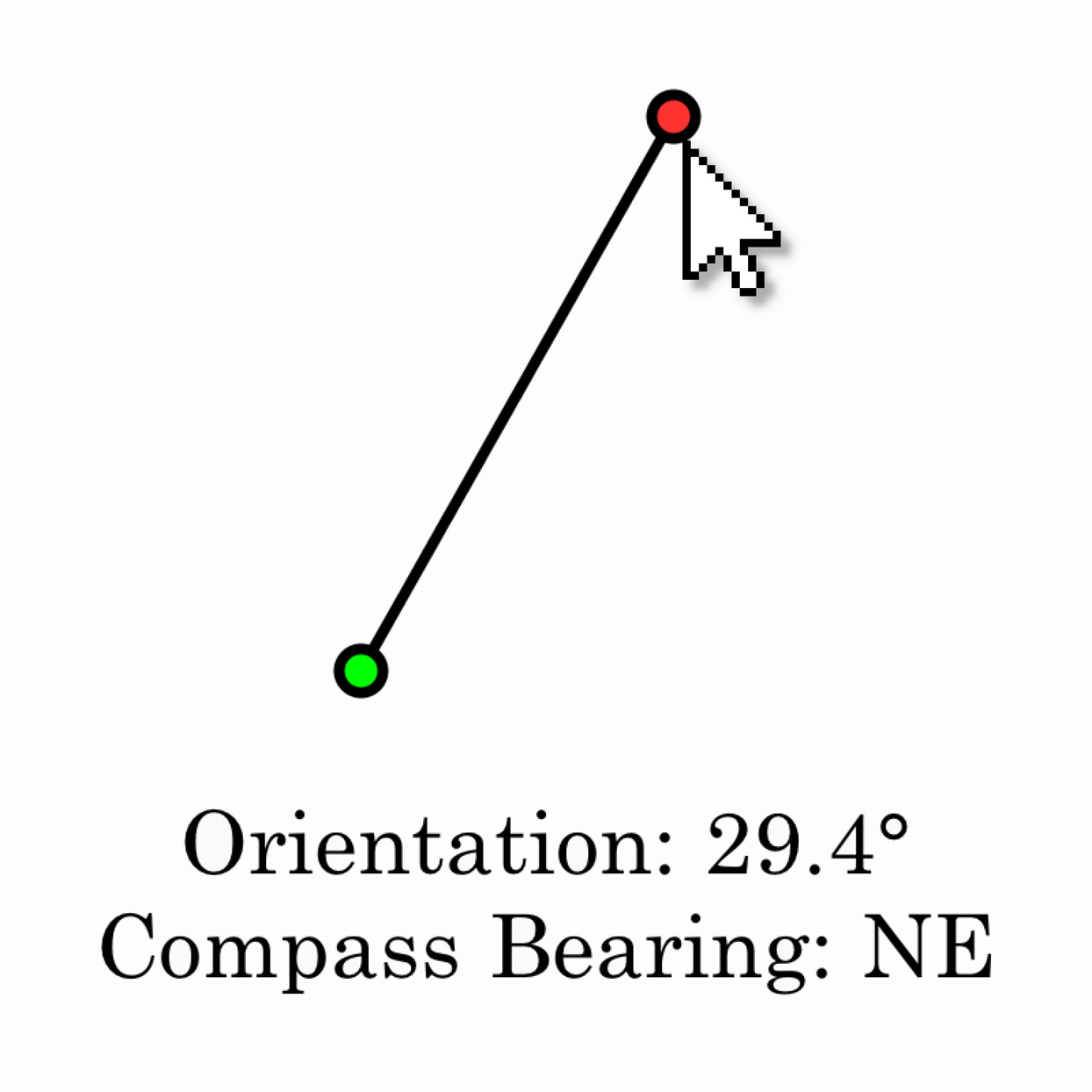
Store the locations of the two most recent mouse clicks and draw a line between them. Using the atan2() function, compute the angular orientation of this line. Display this angle in degrees, and label it with the nearest compass direction (N, NE, E, SE, S, SW, W, NW).
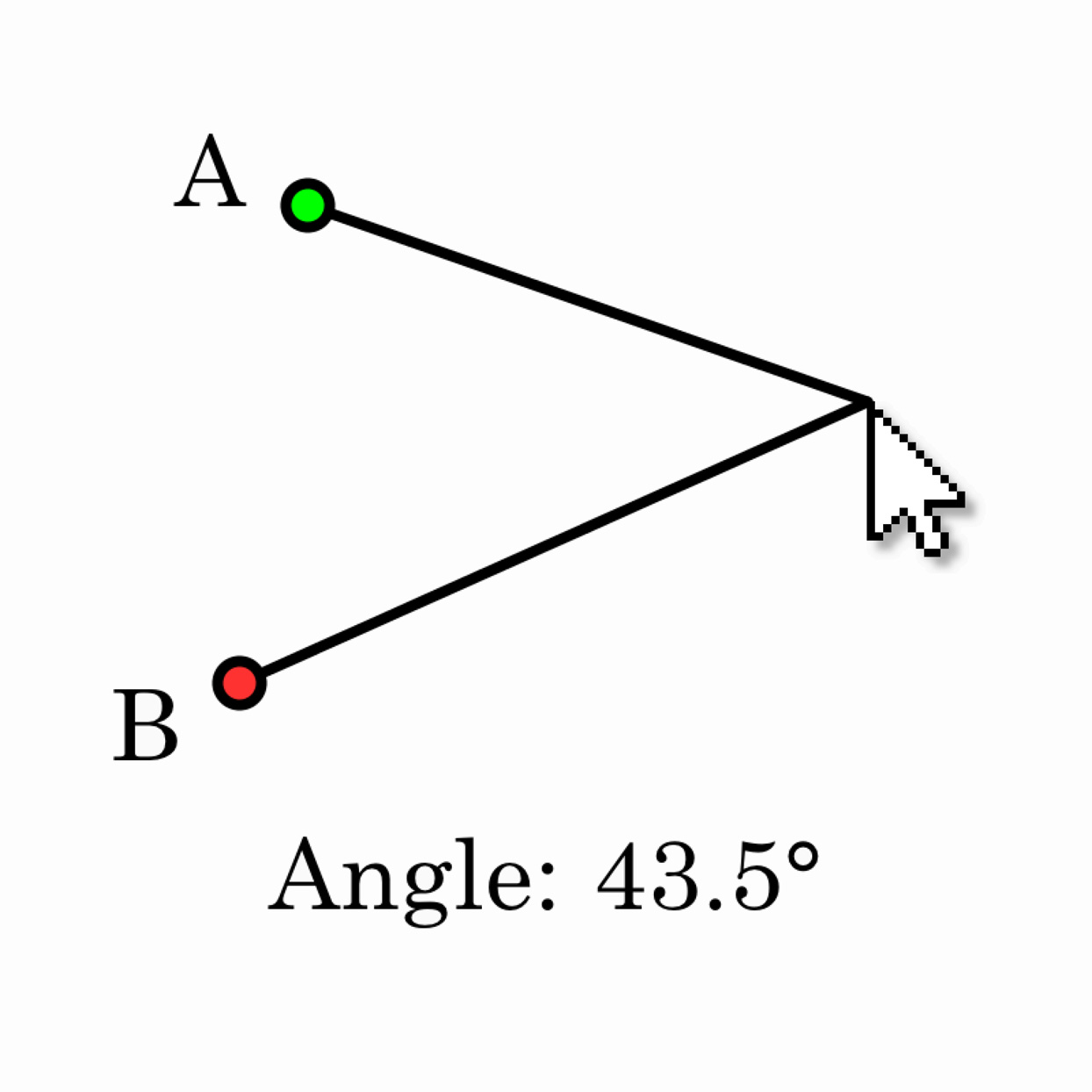
Write a program that computes the angle between three points: two randomly placed points, A and B, and the mouse cursor, C. Hint: Use the dot product to compute the angles, and use the cross product to distinguish positive from negative curvature.
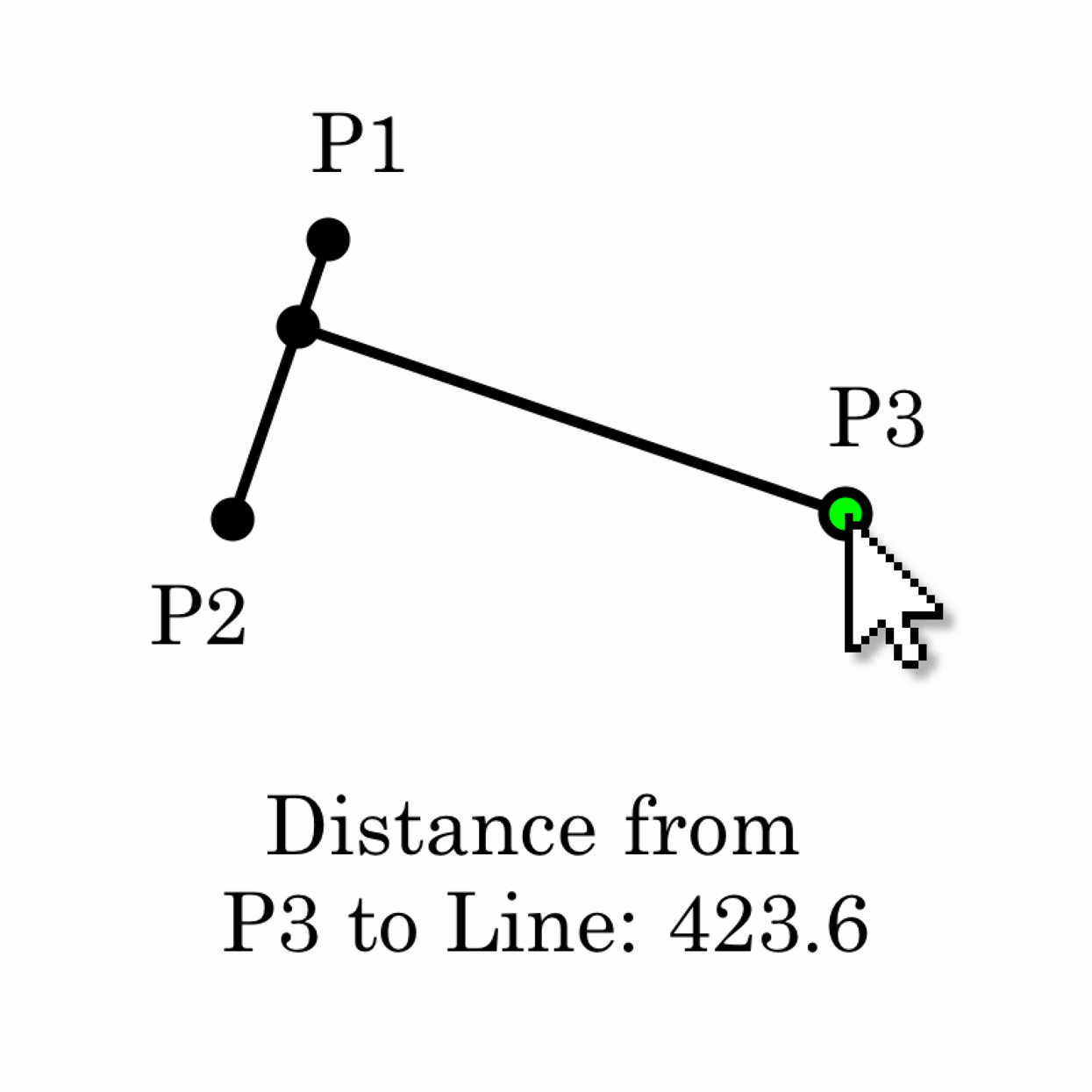
Distance from a Point to a Line
Write a program that creates a random line segment whenever a key is pressed. Compute and display the shortest distance between this line and the cursor. Place a dot at the point on this line that is closest to the cursor.1
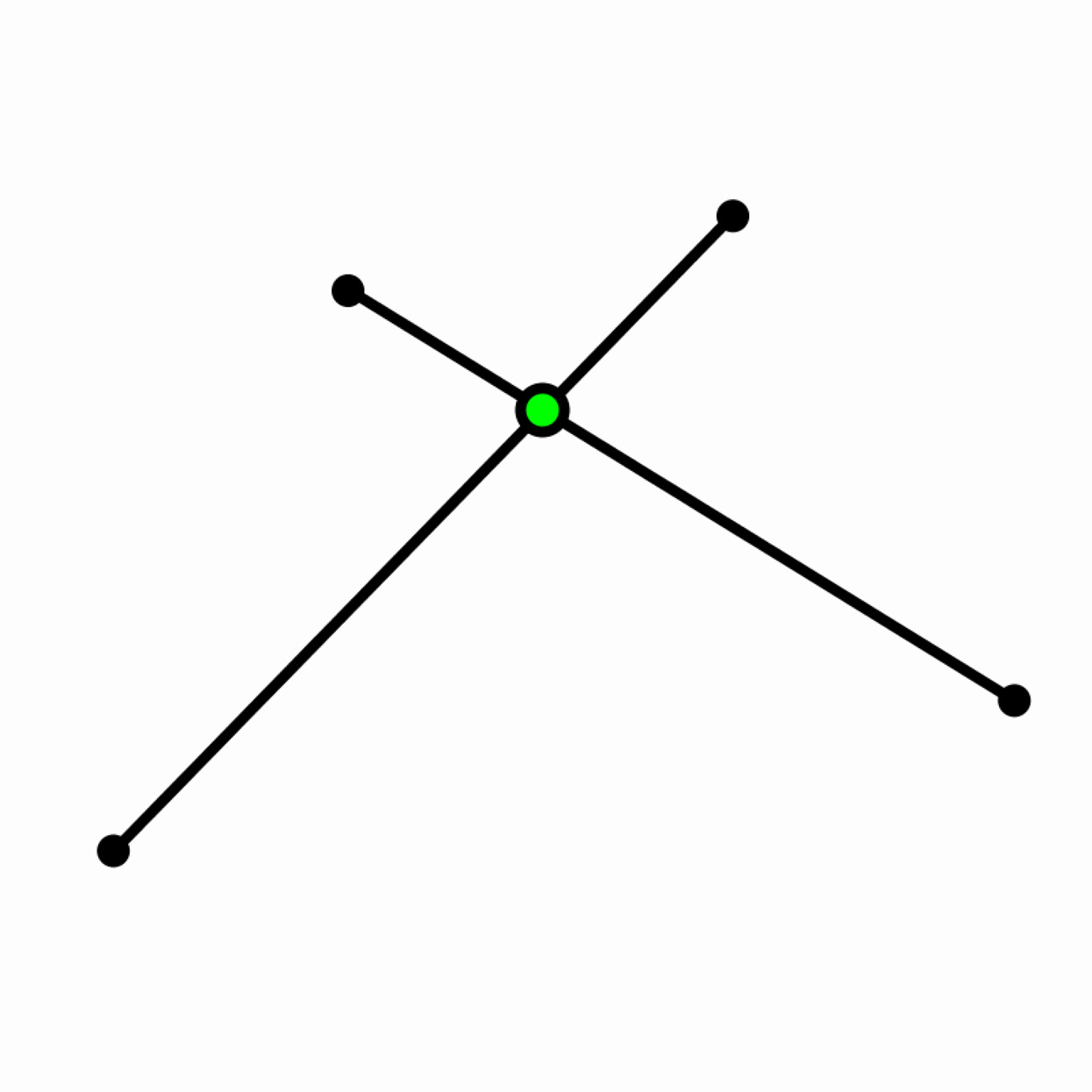
Intersection of Two Line Segments
Write a program that creates two random line segments whenever a button is pressed. Calculate the intersection point of these two line segments, and if it exists, draw a dot there.2
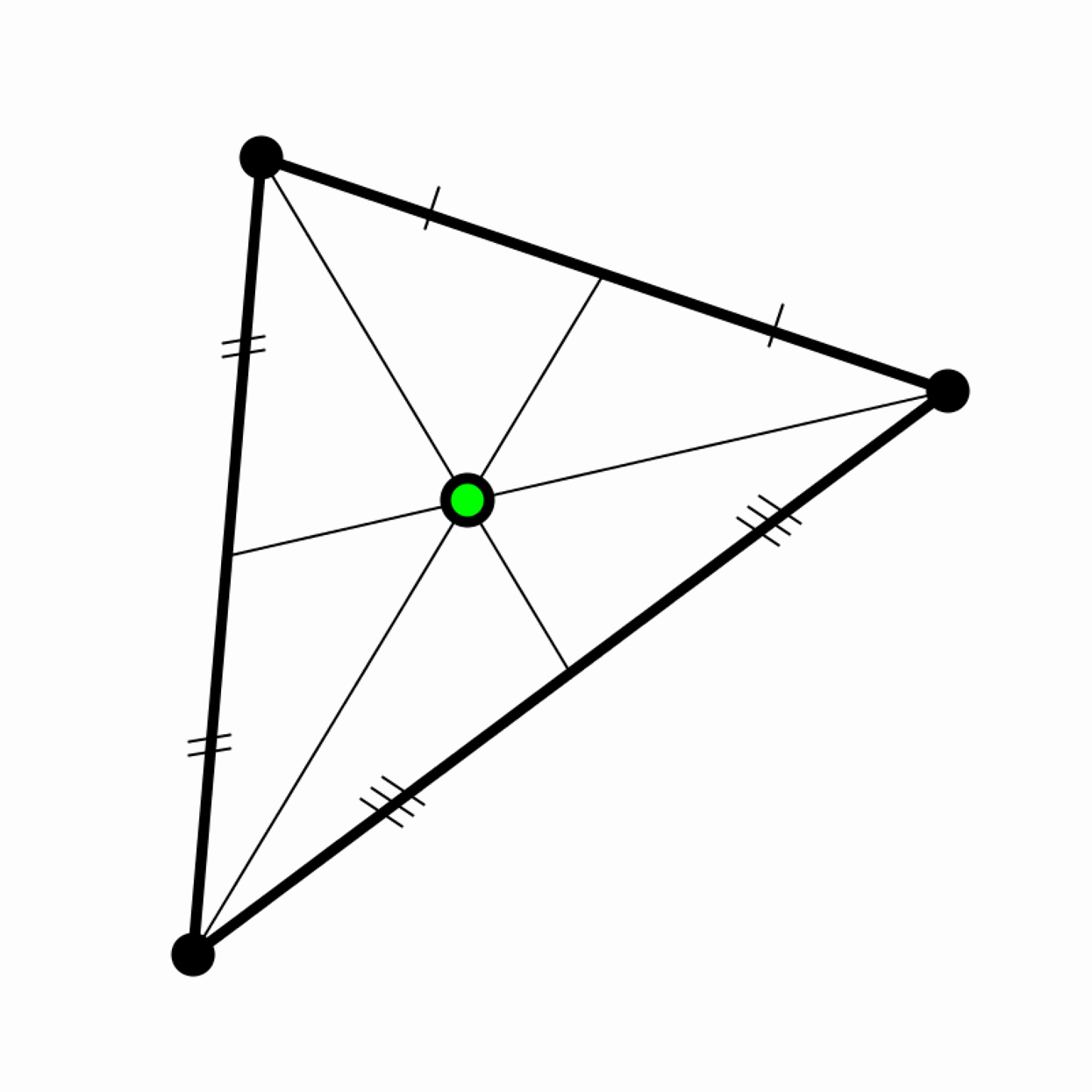
Construct a triangle from three random points whenever a button is pressed. Draw lines (called “medians”) to connect the midpoints of each side to its opposite vertex. At the intersection of these medians is the triangle's centroid. Place a dot there.
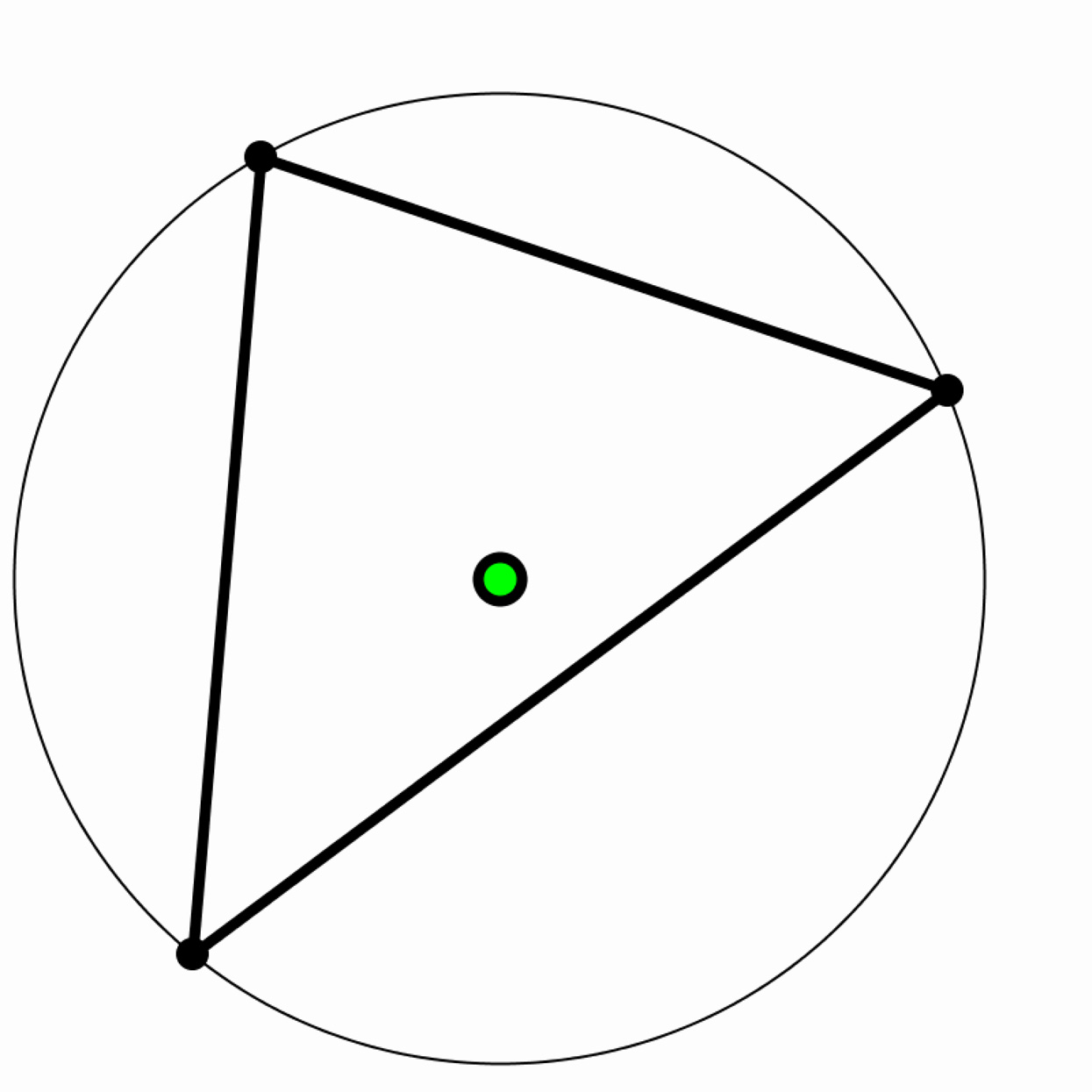
Circle from Three Points (Circumcenter)
Construct a random triangle whenever a button is pressed. Generate a circle that passes precisely through all three of its vertices. The center of this circle is called the circumcenter of the triangle. Place a dot there. Note: the circumcenter is not always inside the triangle.3
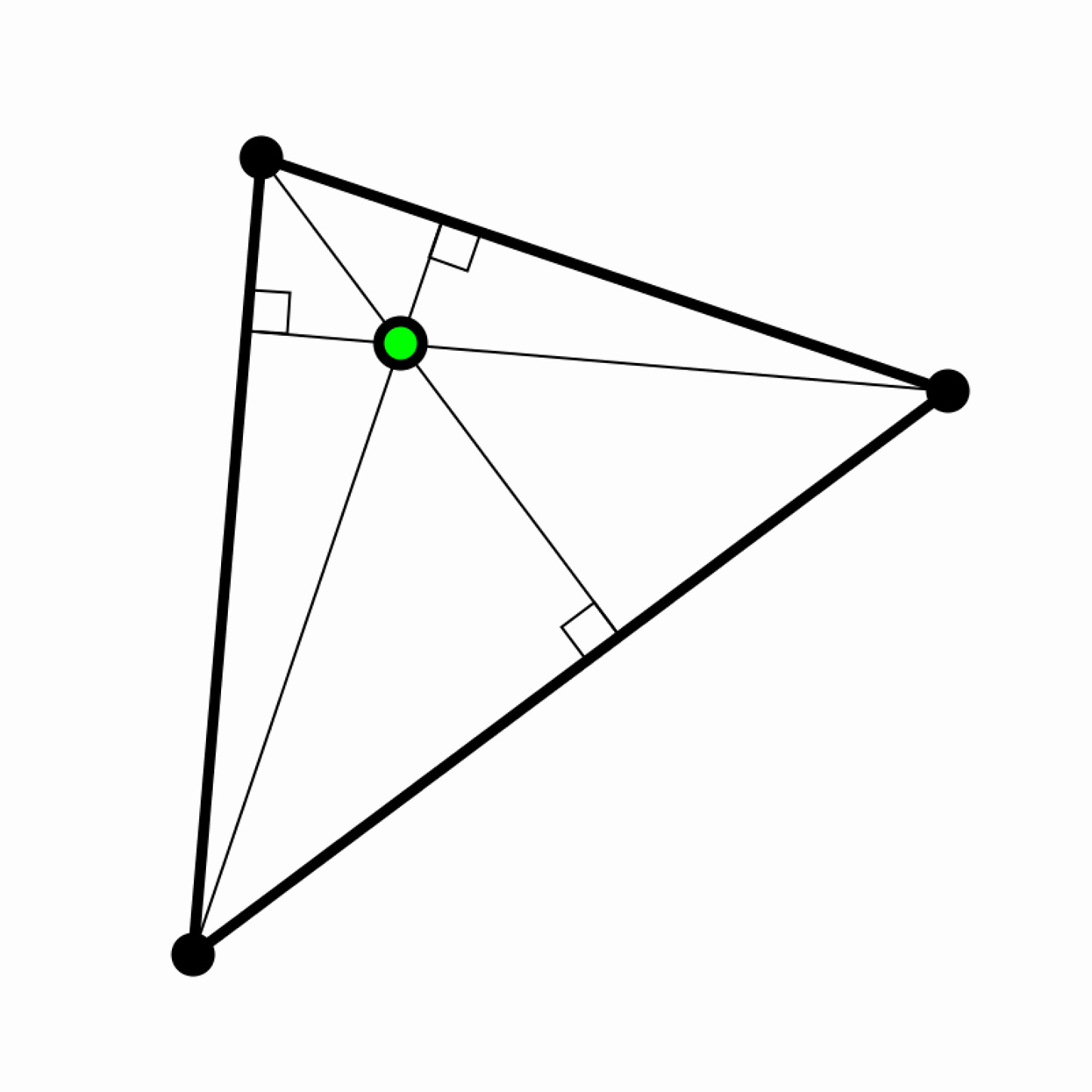
The “altitude” of a triangle is a line that is perpendicular to a given side and passes through the opposite vertex. Write a program that constructs a triangle from three random points whenever a button is pressed. Calculate and display the triangle's three altitudes. The orthocenter of this triangle is located at the intersection of its altitudes. Place a dot there. Note: for most triangles, the altitudes will not pass through the midpoints of the sides.
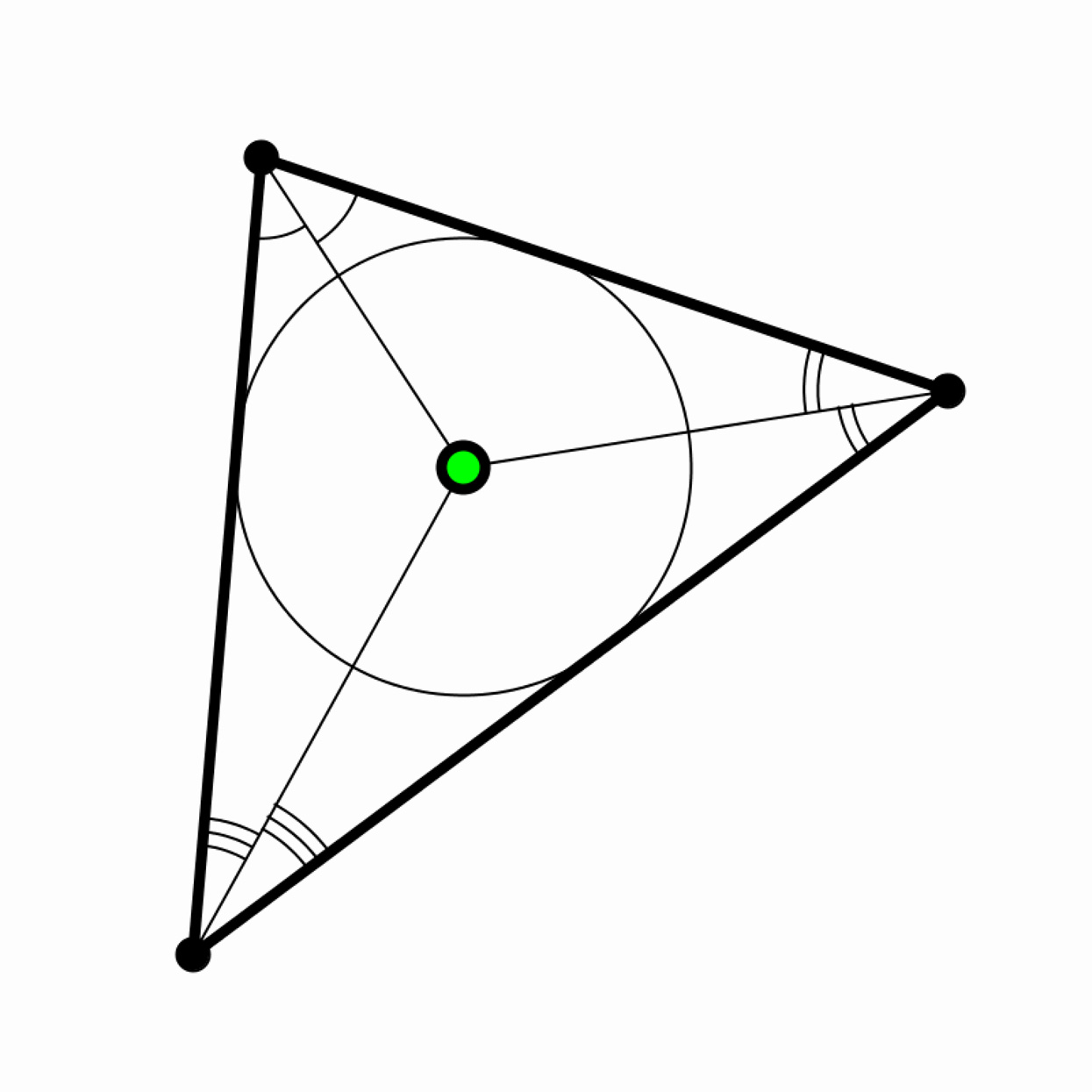
The incenter of a triangle is located at the intersection of the angle bisectors of a triangle's three corners. Write a program that generates a random triangle whenever a button is pressed and places a dot at its incenter. (The incenter also happens to be the center of a circle inscribed inside the triangle, called the incircle; its radius is obtained by dropping a perpendicular line from the incenter to any of the triangle's sides. If you can, draw the triangle's incircle.)