Simulation
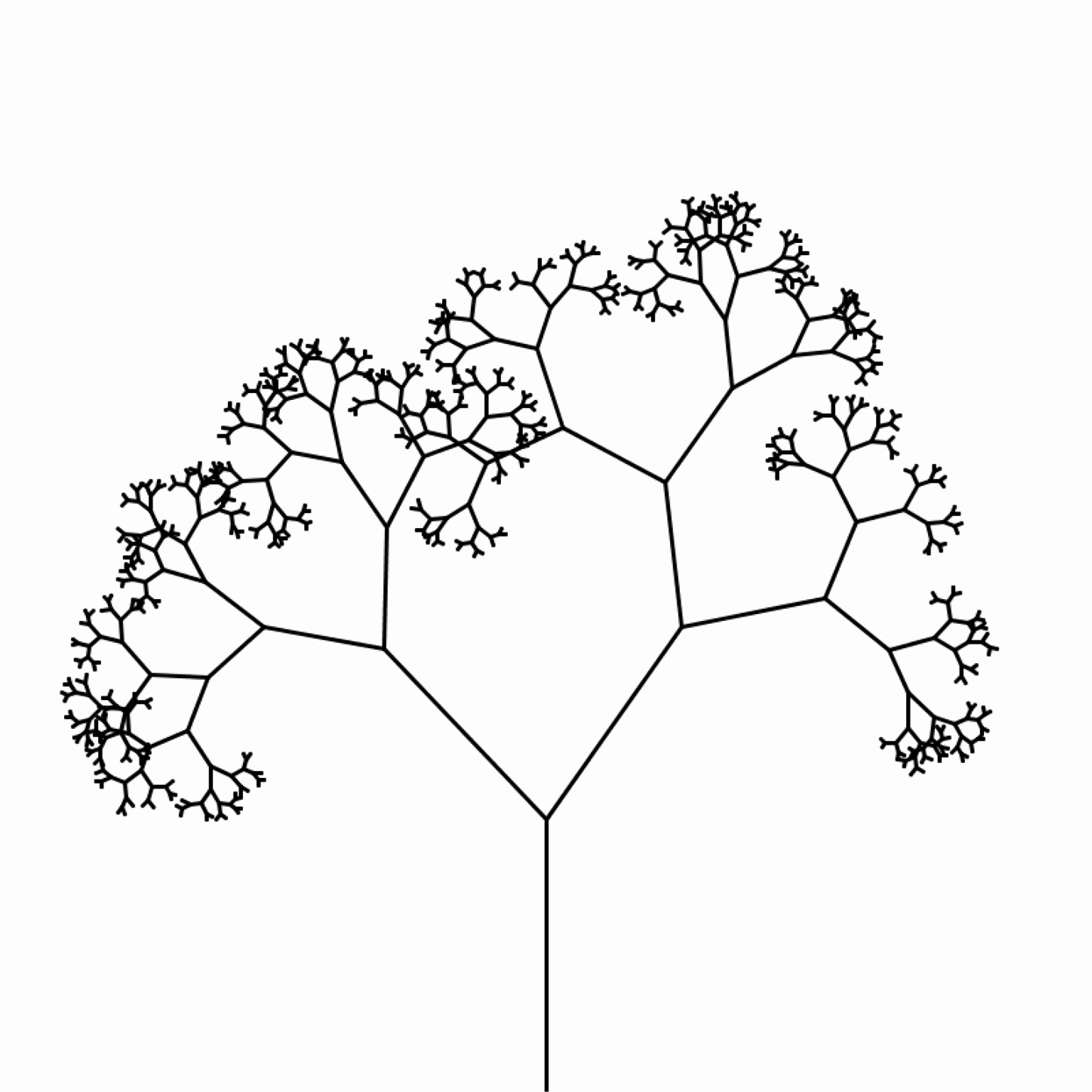
Use recursion to create a tree. Begin with a symmetrical design that repeatedly bifurcates. Introduce a variable that proportionally reduces the length of each iteration's branches, and another to alter their orientation. Explore your tree's possibilities by controlling these variables with the cursor.1

Create a particle class that stores a speck's 2D position and velocity. Add methods to give the particle an initial, randomly generated velocity and constant acceleration. Create an array of particles to simulate a firework. Each element of the array will need to start from the same position.

Create a two-dimensional flock of creatures, modeling your animals as particles that exert (and are affected by) forces of mutual separation (to prevent collision), cohesion (to stick together as a group), and alignment (to orient toward similar directions as their neighbors). Connect your governing parameters to sliders or other UI controls, and observe how changing the relative strengths of these forces alters the behavior of the flock or swarm. Include other forces, such as the desire to flee from a predator, the hunger to hunt for food, etc. Be sure to represent your creatures with a graphic that makes their orientation visible.2
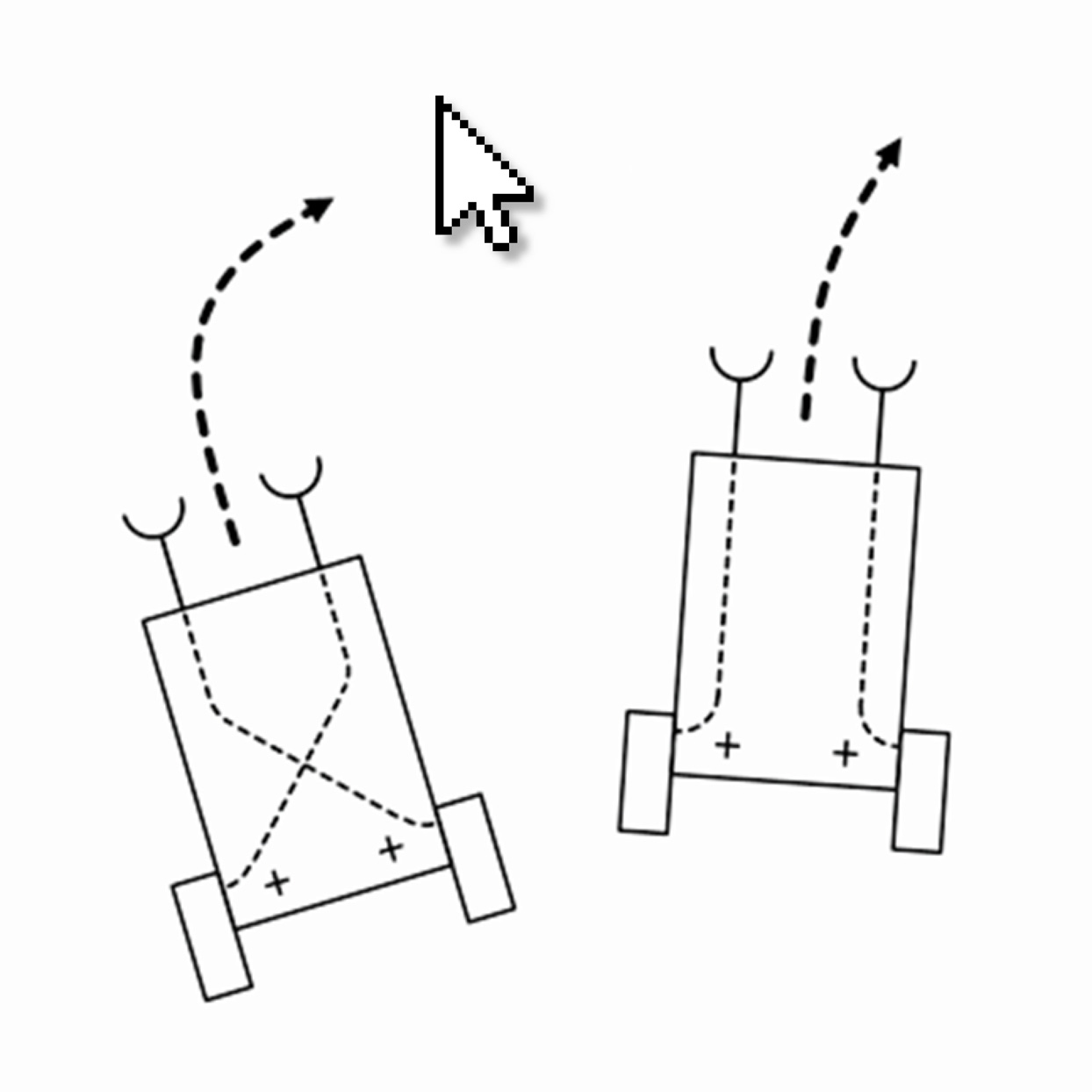
A Braitenberg vehicle is an autonomous agent that moves and steers based on sensor inputs. It measures a stimulus at its location; depending how this signal is mapped to each wheel's power, the vehicle can appear to exhibit different goals and behaviors. Implement vehicles that steer toward or away from the cursor.
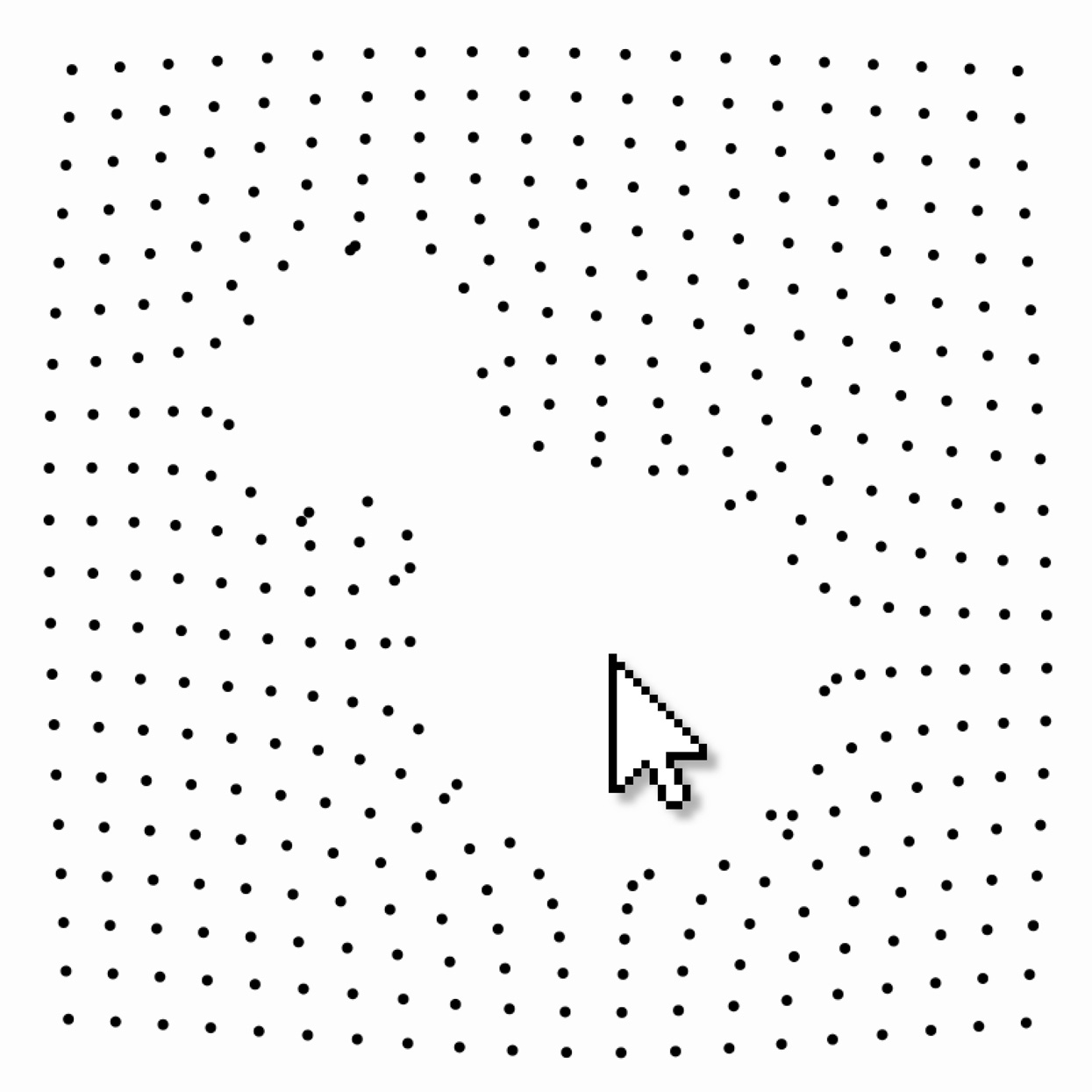
Create a particle class that stores a speck's 2D position and velocity. Add a method that enables a particle's motion to be affected by simulated forces. (See Euler integration and Newton's 2nd Law.) Create an array of particles that are attracted to or repelled by the cursor.
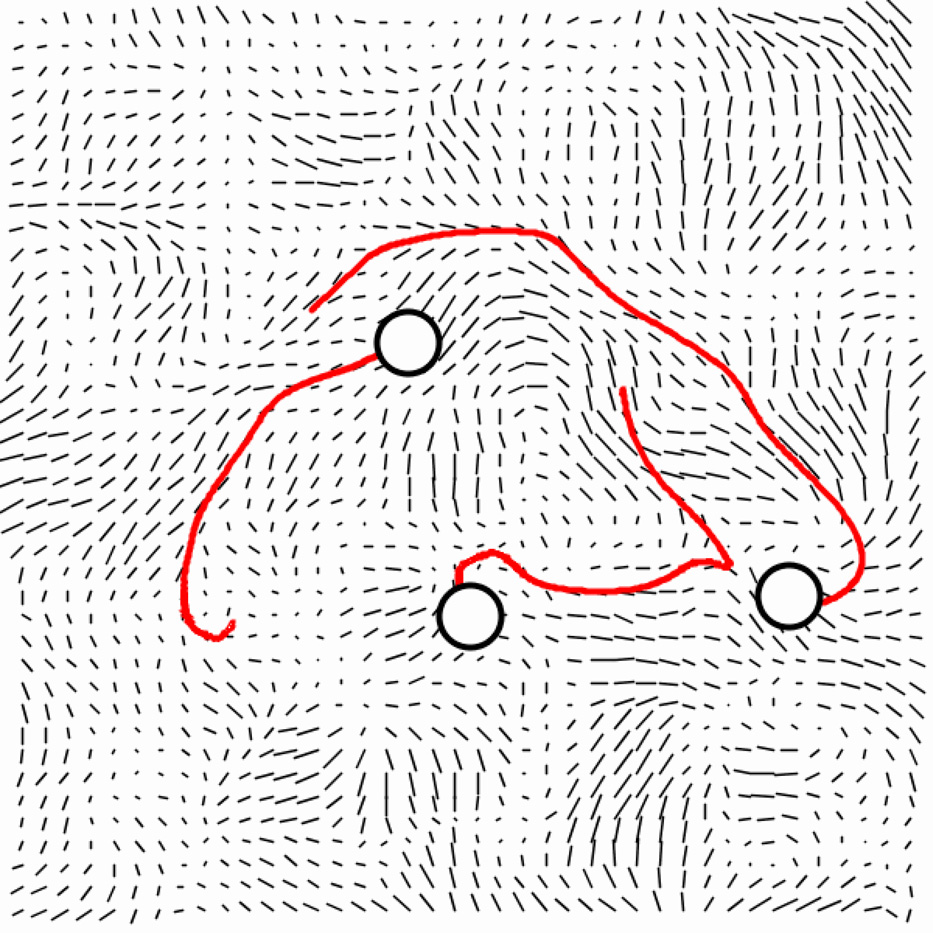
Use 2D Perlin noise to compute a flow field, such that every location on the canvas has an associated x-force and y-force. Place particles into this field, impelling them with the forces at their locations. Make recordings of their traces. Confine the particles with periodic boundaries.
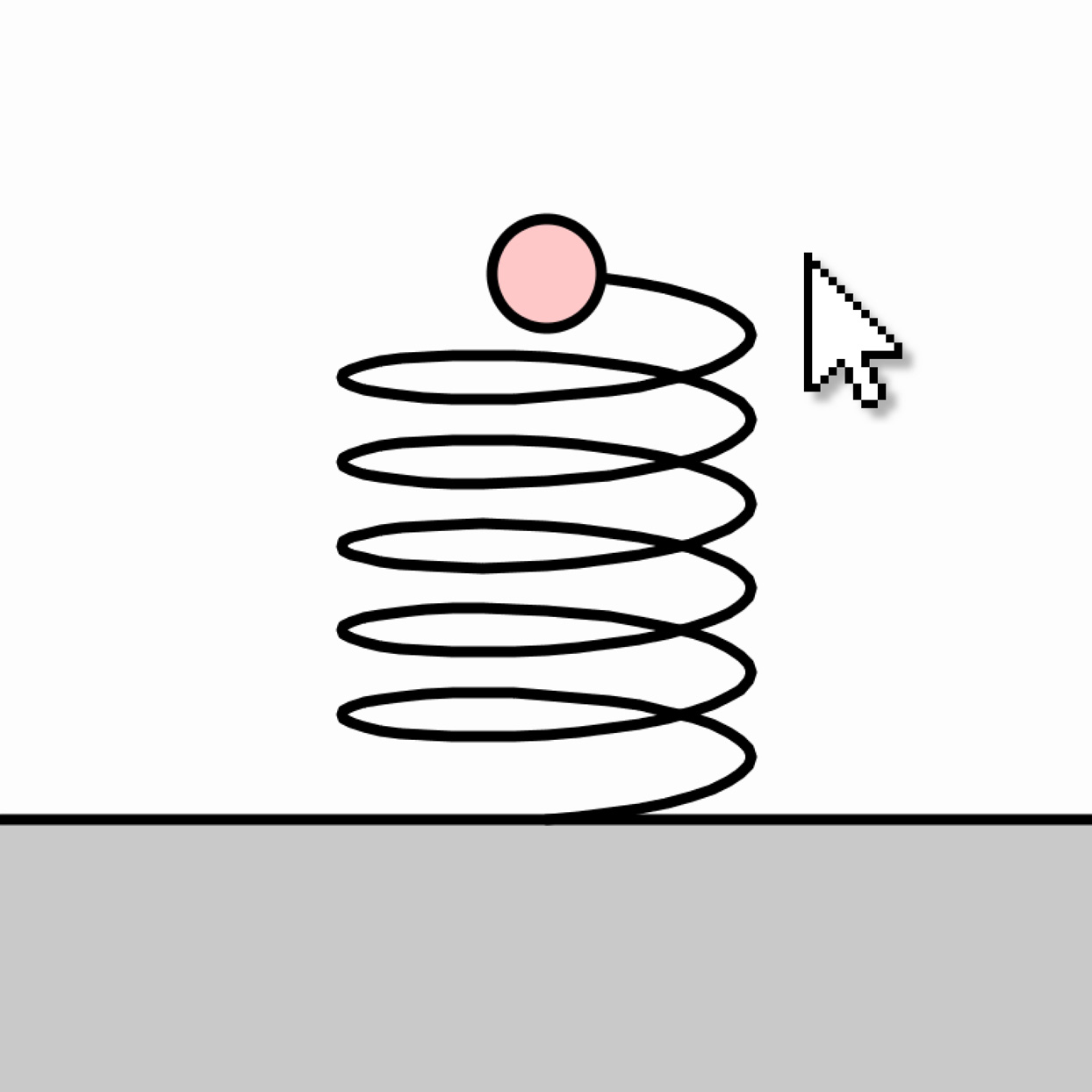
Model a bouncy spring as a particle with a current position P, velocity V, and rest position R. When moved from R, a restorative force F proportional to this displacement pushes it back. Update the particle using Euler integration: add F into V, reduce V by a percentage due to damping, and add V into P.

Generate a “circle packing”: an arrangement of circles such that none overlap, and some (or all) are mutually tangent. In one approach, randomly placed circles are added to unclaimed regions of the canvas and grow until they collide with any previous circles.3
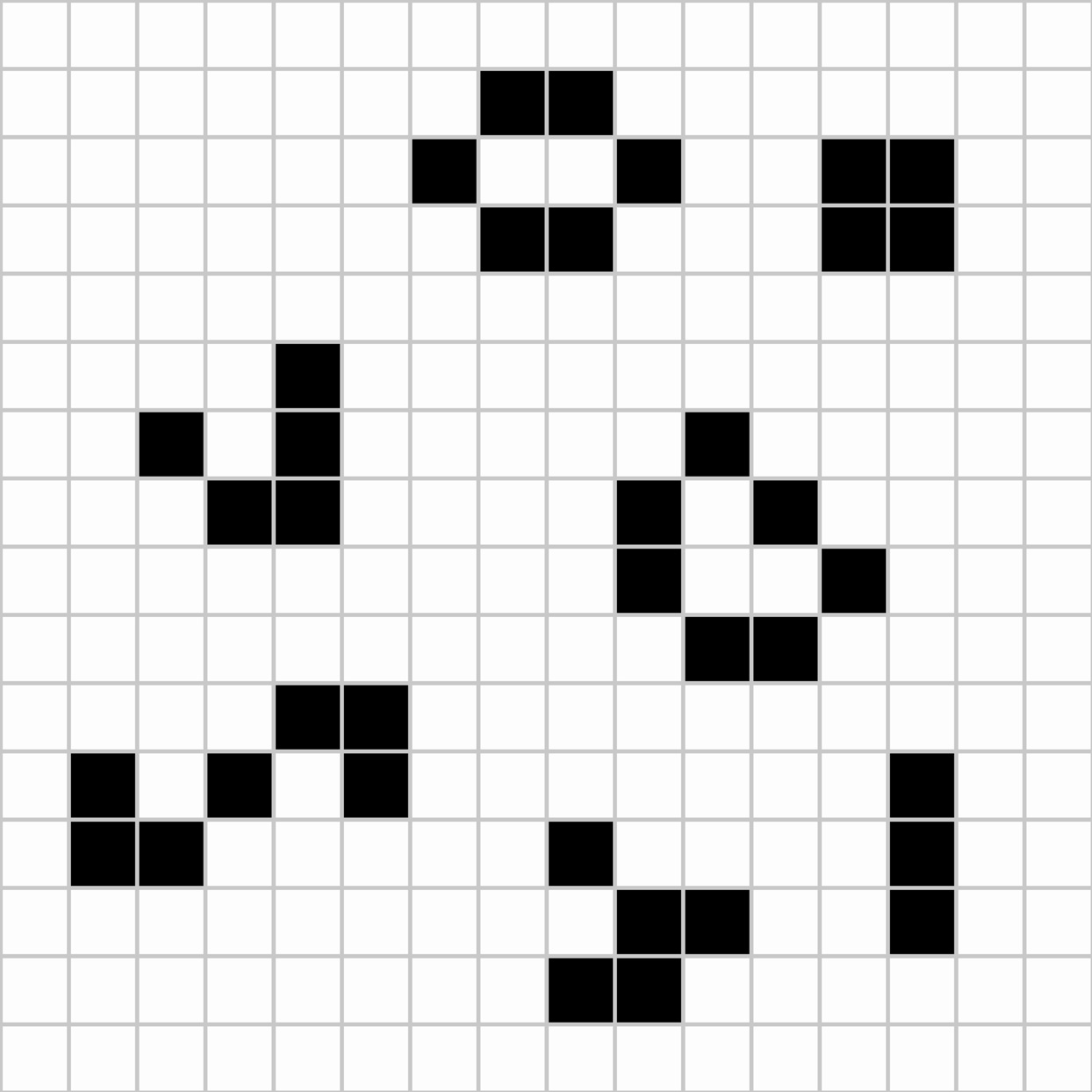
Create an implementation of “Conway's Game of Life.” This classic cellular automaton is one of the simplest and best illustrations of the way in which complex patterns of self-organization can emerge from simple rules.4

Implement and explore the coral forms that arise from diffusion-limited aggregation (DLA): a simulation in which meandering particles become fixed in place when they collide with previously fixed particles (or an initial “seed”).5

Snowflakes are thought to form through a DLA-like process. To make a snowflake generator, modify your DLA simulation from the previous exercise so that it has dihexagonal symmetry.
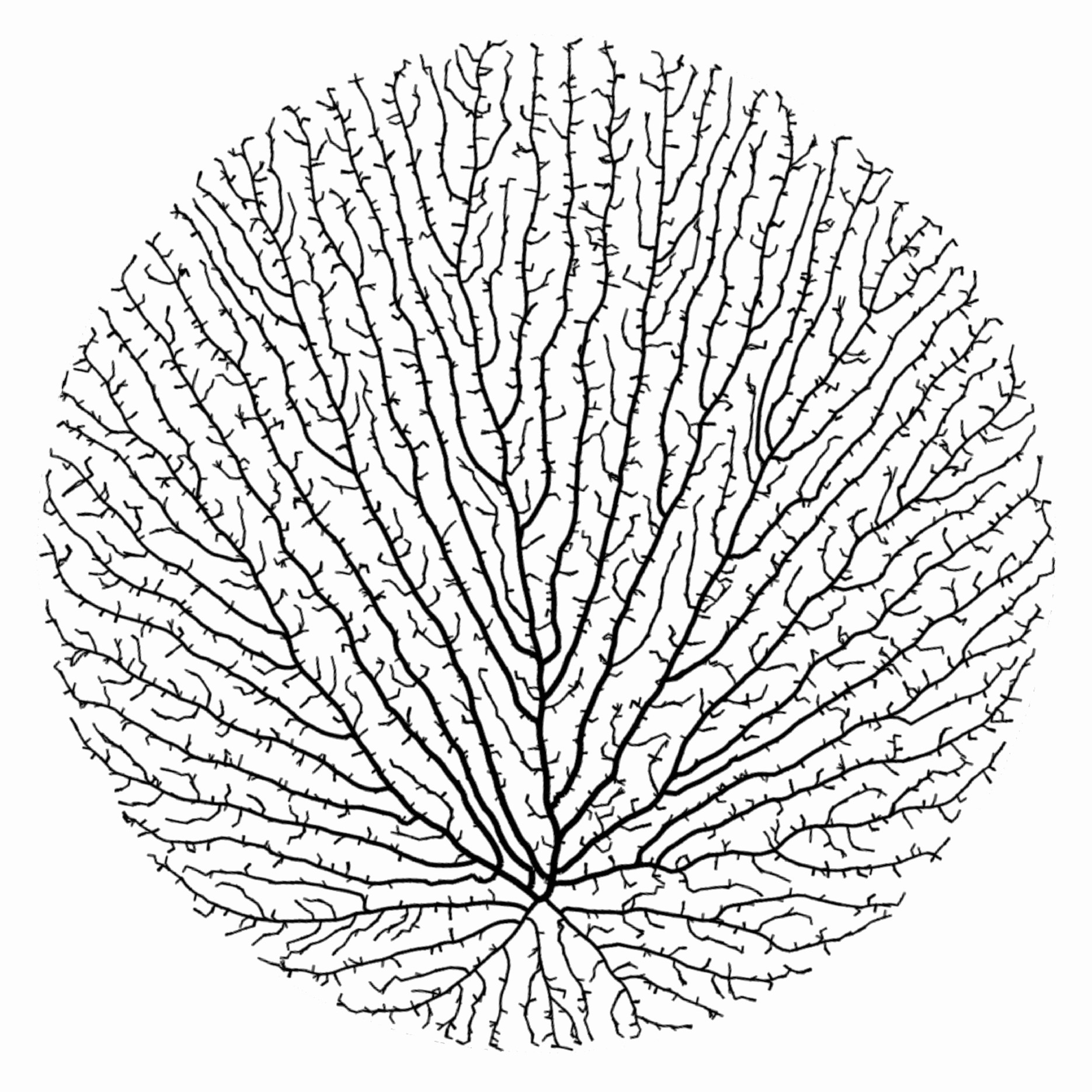
Implement space colonization: an iterative algorithm, first described by Adam Runions, for growing networks of branching line structures based on the locations of “growth hormone” sources to which the lines are attracted.6

Implement differential growth, in which a chain of connected nodes (represented by a curve or polyline) uses simple rules like attraction, repulsion, and alignment to produce meandering shapes. The algorithm uses adaptive subdivision to interpose new nodes when two adjacent nodes get too far apart.6