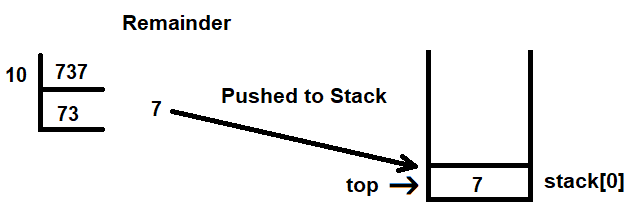
Let's assume that the number we entered is 737. Now, we want to know whether 737 is a palindrome. We will start by applying the mod 10 operator on 737. On application, we will receive the remainder, 7, and the quotient, 73. The remainder, 7, will be pushed to the stack. Before pushing to the stack, however, the value of the top pointer is incremented by 1. The value of top is -1 initially; it is incremented to 0 and the remainder of 7 is pushed to stack[0] (see Figure 3.21 ).
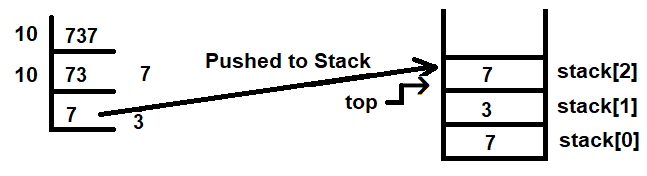
The mod 10 operator returns the last digit of the number as the remainder. The quotient that we get on the application of the mod 10 operator is the original number with its last digit removed. That is, the quotient that we will get on the application of mod 10 operator on 737 is 73:
To the quotient, 73, we will apply the mod 10 operator again. The remainder will be the last digit, which is 3, and the quotient will be 7. The value of top is incremented by 1, making its value 1, and the remainder is pushed to stack[1]. To the quotient, 7, we will again apply the mod 10 operator. Because 7 cannot be divided by 10, 7 itself is returned and is pushed to the stack. Again, before the push operation, the value of top is incremented by 1, making its value 2. The value of 7 will be pushed to stack[2]:
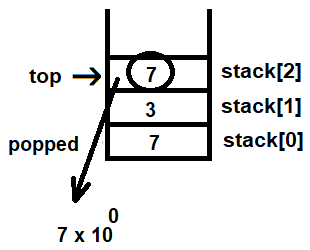
After separating the number into individual digits, we need to pop each digit from the stack one by one and multiply each one by 10 raised to a power. The power will be 0 for the topmost digit on the stack and will increment by 1 after every pop operation. The digit that will be popped from the stack will be the one indicated to by the top pointer. The value of top is 2, so the digit on stack[2] is popped out and is multiplied by 10 raised to power of 0:
After every pop operation, the value of top is decremented by 1 and the value of the power is incremented by 1. The next digit that will be popped out from the stack is the one on stack[1]. That is, 3 will be popped out and multiplied by 10 raised to the power of 1. Thereafter, the value of top will be decremented by 1, that is, the value of top will become 0, and the value of the power will be incremented by 1, that is, the value of the power that was 1 will be incremented to 2. The digit on stack[0] will be popped out and multiplied by 10 raised to the power of 2:
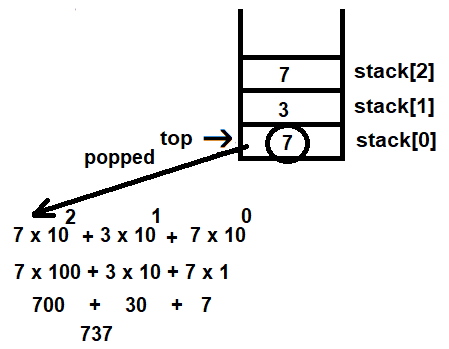
All the digits that are multiplied by 10 raised to the respective power are then summed. Because the result of the computation matches the original number, 737 is a palindrome.
Let's use GCC to compile the findpalindrome.c program, as shown in the following statement:
D:\CBook>gcc findpalindrome.c -o findpalindrome
Let's check whether 123 is a palindrome number:
D:\CBook>./findpalindrome
Enter a number 123
123 is not a palindrome number
Let's check whether 737 is a palindrome number:
D:\CBook>./findpalindrome
Enter a number 737
737 is a palindrome number
Voilà! We've successfully determined whether a number was a palindrome.