Let's assume that the numbers that we need to sort are not greater than 20; so we will define a macro of size 20. You can always assign any value to this macro. Next, we will define an integer array, arr, of size max. You will be prompted to enter how many numbers you wanted to sort. Let's say we want to sort eight values; so the value 8 entered by us will be assigned to a variable, len. Thereafter, you will be asked to enter the eight values that need to be sorted. So, let's say we entered the following values, which were assigned to the arr array:
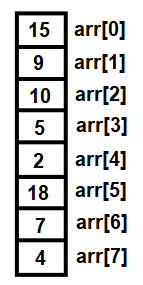
In this sorting method, we will take the help of a nested loop, where the outer loop, i, runs from 1 to 7 and the inner loop, j, runs from the value beginning from i to its value is more than 0. So, in the first iteration of the nested loop, the inner loop will execute only once where the value of i will be 1. The value at the arr[1] index location is compared with that at arr[0]. The tendency is to keep the lower value at the top, so if the value at arr[1] is greater than that at arr[0], the place of the two values will be interchanged. Because 15 is greater than 9 (on the left side of Figure 9.16), the values in the two index locations will be interchanged (on the right side of Figure 9.16) as follows:

After the first iteration, the value of i will be incremented to 2 and the inner loop, j, will run from the value of 2 to 1, that is, the inner loop will execute twice: once with the value of j equal to 2 and then when the value of j is decremented to 1. Within the inner loop, the value at arr[2] will be compared with that at arr[1]. In addition, the value at arr[1] will be compared with that at arr[0]. If arr[2] < arr[1], then interchanging of the values will take place. Similarly, if arr[1] < arr[0], interchanging of their values will take place.
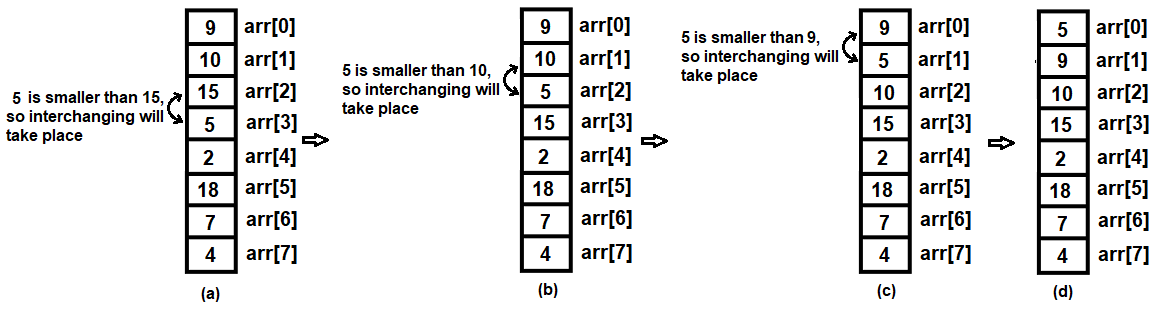
The value at arr[2] that is 10 is less than the value at arr[1], that is, 15; so these values will interchange places (see Figure 9.17). After interchanging the values, we find that the value at arr[1] is greater than the value at arr[0]. So, no interchanging will take place now. Figure 9.17 shows the procedure of the second iteration:

After the second iteration, the value of i will be incremented to 3 and the value of j will run from the values of 3 to 1. Hence, the interchanging of values will take place if the following conditions are met:
- If arr[3] < arr[2]
- If arr[2] < arr[1]
- If arr[1] < arr[0]
You can see in Figure 9.18(a) that arr[3], that is, 5, is smaller than arr[2], that is, 15, so their values will be interchanged. Similarly, the values at arr[2] and arr[1], and then arr[1] and arr[0], will also be interchanged (see Figure 9.18(b) and (c), respectively). Figure 9.18(d) shows the array after all the interchanges have been performed:
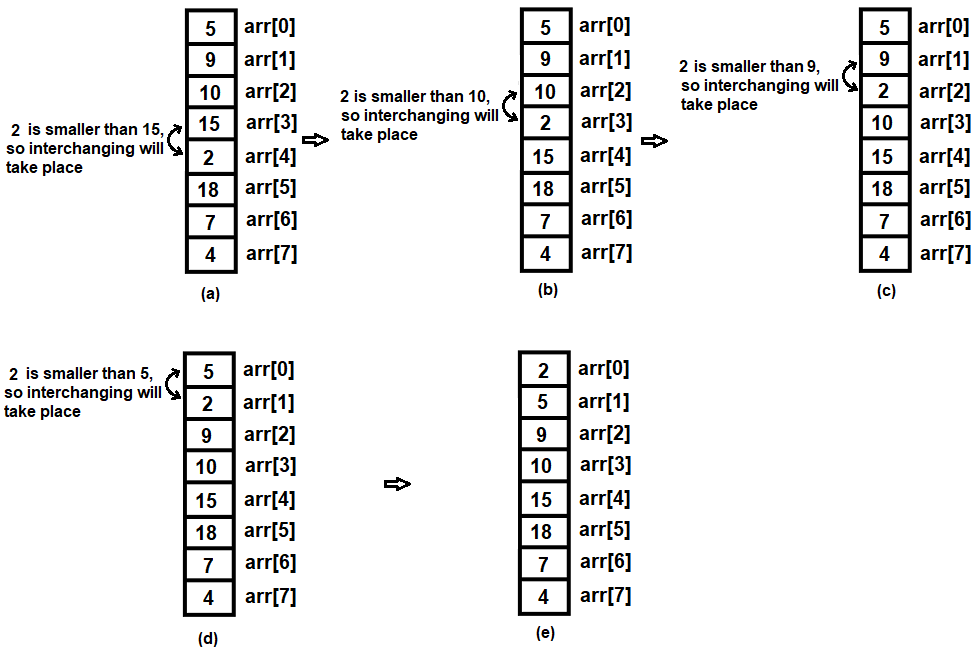
After the third iteration, the value of i will be incremented to 4 and the value of j will run from the values of 4 to 1. So interchanging of values will take place if the following conditions are met:
- If arr[4] < arr[3]
- If arr[3] < arr[2]
- If arr[2] < arr[1]
- If arr[1] < arr[0]
You can see in Figure 9.19 that the main tendency of all these comparisons is to bring the lower values above the larger values in the array:
The same procedure will be followed for the rest of the elements in the array.
The program is compiled using GCC with the following statement:
gcc insertionsort.c -o insertionsort
Because no error appears on compilation, that means the insertionsort.c program has successfully been compiled into the insertionsort.exe file. On execution, it will ask you to specify how many numbers have to be sorted. Following this, the program will prompt us to enter the numbers to be sorted. After entering the numbers, they will appear sorted in ascending order, as shown in the following screenshot:
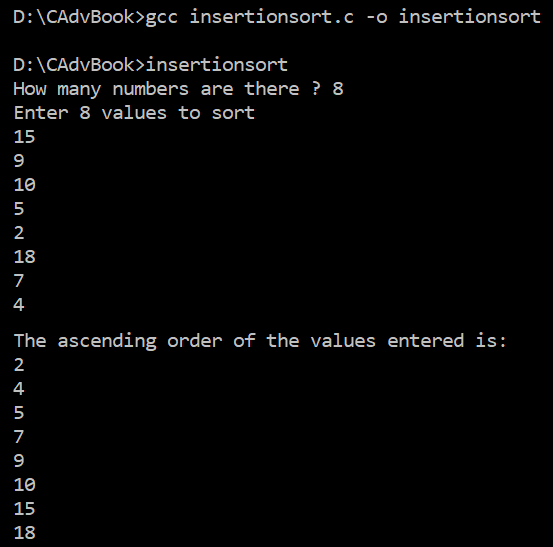
Voilà! We've successfully used insertion sort to arrange numbers in ascending order.
Now let's move on to the next recipe!