We are using the adjacency list representation of the directed graph from the previous recipe, Creating an adjacency list representation of a directed graph:
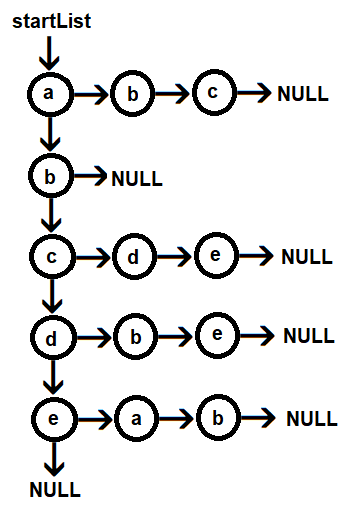
The temp1 pointer is set to point to startList. That is, temp1 is pointing to the node with vertex a. If temp1 is not NULL, the node pointed to by the temp1 pointer is added to the queue. The rear variable, which is -1 at the moment, is incremented to 0 and the a node is added to the array of que nodes at index location 0. Because the value of the front index location is -1 currently, the front is also set to 0, as follows:
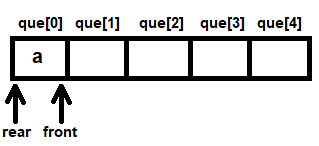
Thereafter, the dequeue function is invoked to remove a node from the queue. Unsurprisingly, the node at the que[0] index location, that is, a, is returned and, because the values of front and rear are the same, the values of the front and rear indices are set to -1, to indicate that the queue is empty again.
The node containing vertex a is returned from the queue and is assigned to the temp3 pointer. The temp1 pointer is set to point to the startList pointer. The marked member of the temp3 node, that is, vertex a, is set to N initially. The vertex name stored in the nme member of the node is displayed, that is, vertex a is displayed on screen.
After displaying vertex a, its marked member is set to Y to indicate that the node is visited and should not be traversed again. The next step is to find the adjacent vertices of vertex a. To do so, the temp2 pointer is set to point to where the edg pointer of temp3 is pointing. The edg pointer of temp3 is pointing at vertex b, so temp2 is set to point at vertex b. Again, the procedure is repeated. If temp2 is not NULL, the b node is queued, that is, it is added to the que[0] index location. Because all of the nodes that are connected to vertex a have to be queued, the temp2 pointer is set to point to the location where its edg pointer is pointing. The edg pointer of node b (in the adjacency list) is pointing to node c, so node c is also inserted into the queue at the que[1] index location as follows:
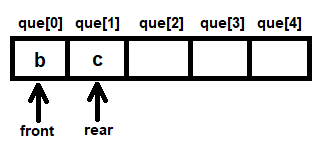
In the queue, nodes b and c are present. Now, again, the dequeue function is invoked; node b is removed from the queue and the temp3 pointer is set to point to it. The temp1 pointer is initially set to point to startList and, thereafter, by making use of its vrt pointer, the temp1 pointer is set to point to vertex b. Because the marked member of node b is N, its vertex name, b, is displayed on screen followed by setting its marked member to Y. A temp2 pointer is set to point to where the edg member of node b is pointing. The edg member of node b is pointing to NULL, so the next node in the queue is accessed, that is, node c is removed from the queue and the temp3 pointer is set to point to it. Because the queue is again empty, the values of the front and rear variables are set to -1.
Again, the temp1 pointer is set to point at vertex c, and the c node is displayed on screen, that is, it is traversed and its marked member is set to Y. So, up until now, nodes a, b, and c are displayed on screen. And the node that is attached to the edg member of c is added to the queue, that is, node d is added to the queue at the que[0] index location. Additionally, the node pointed to by the edg pointer of node d is accessed, that is, node e is also queued or, in other words, added at the que[1] index location as follows:

Node d is removed from the queue and displayed (traversed). The nodes pointed to by their edg member are accessed and, if any of them is marked, then N is added to the queue. The whole procedure is repeated until the queue becomes empty. The sequence in which the vertices are displayed on screen forms the breadth-first traversal of the graph.
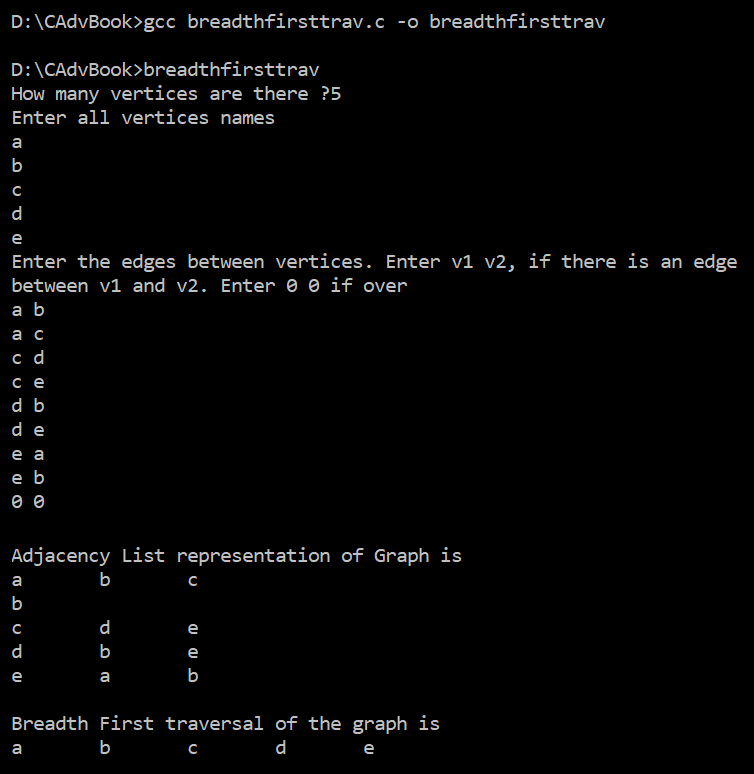
The program is compiled using GCC, as shown in the following screenshot. Because no error appears during the compilation, this means the breadthfirsttrav.c program has successfully compiled into the breadthfirsttrav.exe file. On executing the file, the user will be prompted to specify the count of vertices in the graph, followed by entering the vertices' names. Thereafter, the user is asked to enter the edges of the graph and to enter 0 0 when completed. After the edges of the graph have been entered, the adjacency list representation of the graph will be displayed, followed by the breadth-first traversal of the graph, as shown in the following screenshot:
Now, let's move on to the next recipe!