The first step is to convert the binary number into a decimal number. To do so, we will separate all the binary digits and multiply each by 2 raised to the power of their position in the binary number. We will then apply the mod 10 operator in order to separate the binary number into individual digits. Every time mod 10 is applied to the binary number, its last digit is separated and then pushed to the stack.
Let's assume that the binary number that we need to convert into a hexadecimal format is 110001. We will apply the mod 10 operator to this binary number. The mod operator divides the number and returns the remainder. On application of the mod 10 operator, the last binary digit—in other words the rightmost digit will be returned as the remainder (as is the case with all divisions by 10).
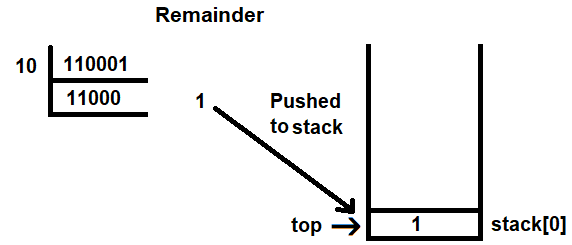
The operation is pushed in the stack at the location indicated by the top pointer. The value of top is initially -1. Before pushing to the stack, the value of top is incremented by 1. So, the value of top increments to 0 and the binary digit that appeared as the remainder (in this case, 1) is pushed to stack[0] (see Figure 3.18), and 11000 is returned as the quotient:
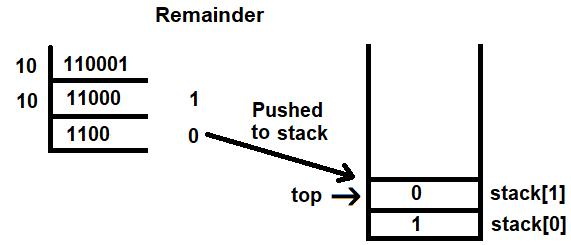
We will again apply the mod 10 operator to the quotient to separate the last digit of the present binary number. This time, 0 will be returned as the remainder and 1100 as the quotient on the application of the mod 10 operator. The remainder is again pushed to the stack. As mentioned before, the value of top is incremented before applying the push operation. As the value of top was 0, it is incremented to 1 and our new remainder, 0, is pushed to stack[1]:
We will repeat this procedure until all the digits of the binary number are separated and pushed to the stack, as follows:
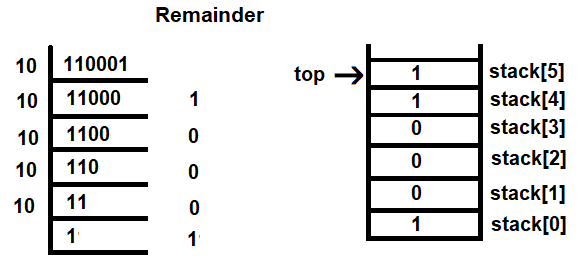
Once that's done, the next step is to pop the digits out one by one and multiply every digit by 2 raised to the power of top. For example, 2 raised to the power of top means 2 will be raised to the value of the index location from where the binary digit was popped off. The value from the stack is popped out from the location indicated by top.
The value of top is currently 5, hence the element at stack[5] will be popped out and multiplied by 2 raised to the power 5, as follows:
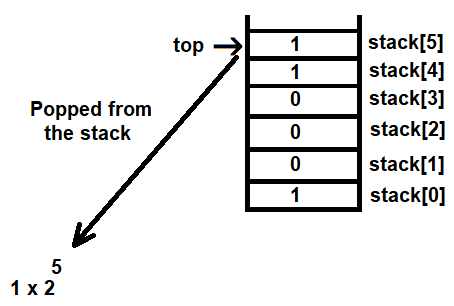
After popping a value from the stack, the value of top is decremented by 1 to point at the next element to be popped out. The procedure is repeated until every digit is popped out and multiplied by 2 raised to the power of its top location value. Figure 3.19 shows how all the binary digits are popped from the stack and multiplied by 2 raised to the power of top:
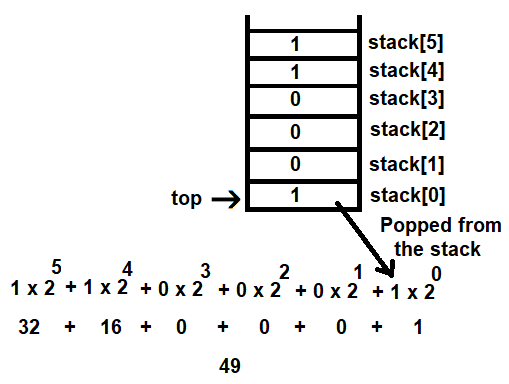
The resulting number we get is the decimal equivalent of the binary number that was entered by the user.
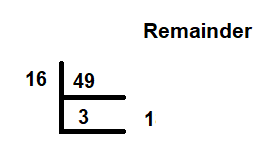
Now, to convert a decimal number into a hexadecimal format, we will divide it by 16. We need to keep dividing the number until the quotient becomes smaller than 16. The remainders of the division are displayed in LIFO order. If the remainder is below 10, it is displayed as is; otherwise, its equivalent letter is displayed. You can use the preceding table to find the equivalent letter if you get a remainder between 10 and 15.
In the following figure, you can see that the decimal number 49 is divided by 16. The remainders are displayed in LIFO order to display the hexadecimal, hence 31 is the hexadecimal of the binary number 110001. You don’t need to apply the preceding table as both the remainders are less than 10:
Let's use GCC to compile the binaryintohexa.c program, as follows:
D:\CBook>gcc binaryintohexa.c -o binaryintohexa
Here is one output of the program:
D:\CBook>./binaryintohexa
Enter a number in binary number 110001
The decimal of binary number 110001 is 49
The hexa decimal format of binary number 110001 is 31
Here is another output of the program:
D:\CBook>./binaryintohexa
Enter a number in binary number 11100
The decimal of binary number 11100 is 28
The hexa decimal format of binary number 11100 is 1C
Voilà! We've successfully converted a binary number into a hexadecimal number.
Now, let's move on to the next recipe!