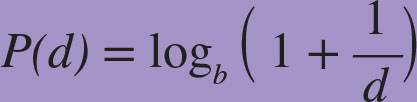BENFORD’S LAW

In a numerical dataset, you might expect the leading digits of each number to be evenly distributed. In fact, lower-value digits are much more likely than higher digits.

WHAT IS IT?

The phenomenon was first seen by American astronomer Simon Newcombe in the 1880s. It was rediscovered and popularized in 1938 by the physicist and engineer Frank Benford.

He found that the leading digits of numbers in a real-life dataset are distributed as follows:

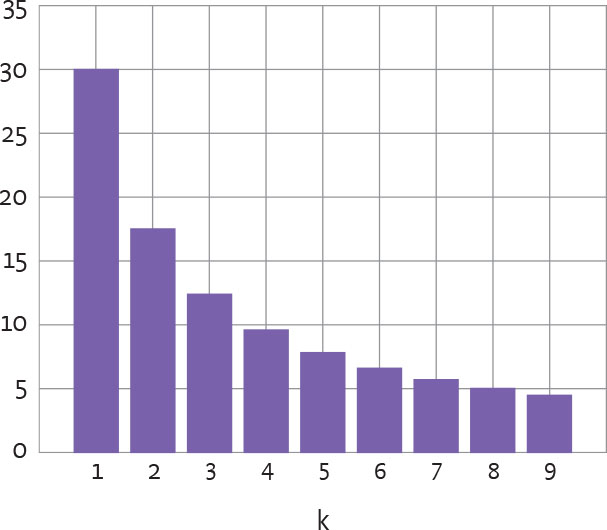
So, the leading digit is 30 percent likely to be a “1” but less than 5 percent likely to be a “9.”

Benford tested the law on many datasets, including constants of nature, population statistics, life expectancies, and the sizes of rivers.

FORMULA

Benford’s law can be framed as a formula. The leading digit d, for numbers expressed in base b, occurs with probability

The law is most pronounced in large datasets containing numbers that span several orders of magnitude. At the time of writing, a full explanation has yet to be found.

FRAUD DETECTION

This stark contrast between a real-life set of numbers, and one that’s been invented or generated randomly, has found an application in spotting fraudsters. The distribution of digits in a fabricated table of accounts, for example, generally will not follow the pattern of Benford’s law.

RELATED EFFECTS

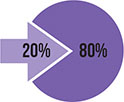
The Pareto principle: also known as the eighty–twenty rule, this states that 80 percent of monetary wealth is typically owned by 20 percent of the population.

Zipf’s law: the frequency of a word in a text is inversely proportional to its rank. So the nth most common word will occur with a probability proportional to 1/n.

Price’s law: half of the publications in a given field are written by the square root of all authors in that field. So if there are a hundred authors, half of all the literature will be written by ten of them.