As Planck recovered from surgery, the Allies took Rome on June 5 and swarmed the beaches of Normandy on the sixth. Most Germans could see an end to the war methodically approaching, despite Nazi propaganda.
In early July, Max Planck donned his once-familiar tuxedo and traveled to Berlin for a scientific celebration. The Prussian Academy of Sciences would, for one night, try to turn away from the darkness surrounding them and celebrate an anniversary. The Reich’s top physicist and director of their atomic research program, Werner Heisenberg, organized the event. Heisenberg collected Max Planck at his Berlin hotel and attempted to drive them to the banquet hall, but nothing in the wrecked landscape was familiar. Neither of them could recognize the streets of Berlin. After asking for help, they finally found the correct address, but once more thought they were lost. “We ended up with our car in front of a giant pile of rubble with bent iron rods and concrete blocks,” Heisenberg recalled. After further inquiries, they were shown a path through the dusty, jagged debris, navigating the ruins of the empire, climbing and squeezing their way to an open door. Inside, the surviving banquet room was lively and intact like a sharp memory. When Planck entered, the assembled grew silent. “Each greeted Planck with worship, and you could see so clearly how much love streamed to this man,” Heisenberg said. “And you could also feel that he himself was happy to see the familiar faces once again. The string quartet began to play, and for an hour or two the old times returned, the cultured Berlin where Planck, of course, was the leading figure.” A large gathering of friends and remnant scientists welcomed the guest of honor and toasted the fiftieth anniversary of Geheimrat Professor Doktor Planck’s induction to the Prussian Academy of Sciences. At the lead table, Max was particularly pleased to find himself seated next to Erwin.1
Why, 50 years later, had Planck become such a pervasive scientific name? How had the young student showing great aptitude for everything, but superlative ability in nothing, risen to such influence?
Though he possessed a remarkable mind, it is difficult to label Planck a genius in the end. “Unfortunately,” he later said, “I have not been given the capacity to react quickly to intellectual stimulation.” Planck had never been at the top of his class as a student—rather, his teachers noted his winning people skills.2 What Planck did possess as a scientist was an uncommon brand of focus, an unmatched mental rigor. He continually honed his concentration’s sharp edge in the furnace of faith. He knew in his bones that nature operated by some logical system, and he devoted himself to uncovering that system, no matter the obstacles or consequences.
The transformation from a solid but not-necessarily-distinguished physicist to the enshrined Max Planck began sharply in 1894. His former professor and friend Hermann von Helmholtz nominated Planck for full membership to the Academy. He claimed that Max, then 36, had made substantial contributions to physics. Most notably, Helmholtz wrote, Planck had made his mark on the field of physical chemistry without the chemists’ deplorable dependence on the concept of atoms.3 Planck had used pure thermodynamics, assuming only continuous matter (no grains or atoms), to probe with his pen and paper everything from phase transitions to the behavior of fluids conducting electricity. His entire career to 1894 had been devoted to thermodynamics, with special allegiance to the second law and entropy.
In truth, Max Planck’s thinking was changed by working on and thinking about problems of chemistry. Quietly and methodically, he had come to accept “atomism,” unlike most other physicists. The switch to embracing atoms was the first of many major shifts in his thinking, and to his great credit, this flexibility was a hallmark of Planck. So many academics sink roots into their favorite topic and convictions, but Planck was able to move to a more sensible spot, following the sunshine and the most fertile soil.
In 1882, the young physicist held a common view. Atomic theory, he said, “will ultimately have to be abandoned in favor of the assumption of continuous matter.” In the same year, he ended his paper “Vaporization, Melting and Sublimation,” by noting, “The mechanical theory of heat is incompatible with the assumption of finite atoms.”4 Statements of this kind were music to the establishment’s ears. The idea of “continuous matter” is difficult to take seriously in the twenty-first century, but it passed the sniff test for many previous centuries: Most scientists assumed that given a sharp enough and small enough knife, they could always cut a tiny object into ever smaller pieces. A huge advantage of this assumption was mathematical, as Newton’s calculus could reign supreme in describing continuous matter. But in 1884, the Swedish chemist Svante Arrhenius made a breakthrough proposition to describe the electrical properties of certain solutions. He suggested that atoms drifting in water could become ionized, and thereby electrically charged. In the same year, Jacobus van’t Hoff published Studies in Chemical Dynamics, similarly grounded in the assumption of atoms. And so by 1887, as Planck toiled within these topics, he had changed his mind. And in 1890, he wrote to a colleague that physicists had no choice: If they wanted to examine certain problems, they had to accept atoms and molecules as a given.5
In 1894, Max was already a full professor (rank of Ordentlicher Professor). The ascension to the Berlin Academy must have felt like cresting one of the mountains he confronted every summer, and at last he found himself embraced by the establishment. His reputation was solid if not spectacular. In five years, he had steadied himself and his family in Berlin. He and Marie celebrated the first birthday of their last baby Erwin. The city itself was abuzz with new electric lighting and a growing number of telephones. Amazed audiences watched Ottomar Anschütz project silent moving pictures of athletes and soldiers trotting their horses. Berlin’s well-to-do tinkered with new technologies and anticipated more. Students began filling the seats of science courses like never before.
At the same time, German physics suffered a sudden leadership vacuum. By the end of 1894, both the renowned Hermann von Helmholtz and also the rising genius Heinrich Hertz would be dead.
As described earlier, Max Planck was poised for a new challenge. He was now versed in the problem of black-body radiation, which hinted at universal truths, and in looking around Berlin he saw the world’s leading experts collecting black-body measurements, just waiting for a theory to explain their results. Most importantly, he had identified what he considered the single most important problem in physics: reconciling thermodynamics with mechanics. In the former, his home turf, one could define an arrow of time. As entropy gradually increases, moments tumble irreversibly on the heels of prior moments, all according to the second law. But the new “gas theory,” a microscopic version of mechanics, didn’t fit with the second law. This statistical approach of Maxwell and Boltzmann gambled with reality—it placed odds on different configurations of jittering, colliding, and spinning gas molecules. Here, physicists could discuss an average quantity for trillions of tiny particles, or a spread of possible options. Instead of one exact snapshot of a system sliding irreversibly and necessarily to the next, a system in gas theory rattled and hummed from point A to point B, most probably, but there was always a chance it could find point C or D instead. And sometimes, moving from point A to point C or D could rupture the second law. In 1895, Boltzmann wrote that, “The probability of such cases is not mathematically zero, only extremely small.” Max, on the other hand, felt great loyalty to the ideas of Clausius. “At that time, I thought the principle of entropy increase was valid without exception, like the principle of energy conservation,” he wrote late in life, “while for Boltzmann this principle was only a law of probability and thus subject to exceptions.”
Max had a difficult professional relationship with the more emotional Boltzmann. In the early 1890s, despite his conversion to atomism, he still thought that much of Boltzmann’s work was, “inadequately rewarded by the fruitlessness of the results gained.”6 In essence, he said gas theory looks very impressive, but it’s all sound and fury so far. The sensitive and mercurial Boltzmann took offense, and to Max’s astonishment, he publicly questioned Planck’s judgment during a subsequent conference.7
Prickly interactions aside, Planck was now hooked on the problem. How could he reconcile the beloved second law of thermodynamics with the sensible and increasingly successful statistical approaches? Even while the number of people following the dilemma could have been tallied on one hand, Max relished its relative obscurity. “It was an odd jest of fate,” he wrote later. “The lack of interest of my colleagues … turned out to be an outright boon. … As the significance of the concept of entropy had not yet come to be fully appreciated, nobody paid any attention to the method adopted by me, and I could work out my calculations completely at my leisure, with absolute thoroughness, without fear of interference or competition.”8
Planck turned his full focus to the mysterious and universal curves of black-body radiation, which he intuited as the perfect battleground for thermodynamics and the new mechanics. Thermodynamics would be key since the brightness and colors of the emitted light depended precisely on the temperature. He would also need some of the new techniques of Boltzmann and Maxwell. The molecules of the black body roiled in some sort of statistical reality, with various energies and vibrations, and somehow they gave rise to the exact spectrum of emitted light. By analogy, imagine a crowded stadium at a football game. If we wish to completely understand the roar emanating from the stadium, a physicist can start by building a model of the fans in the seats. She gives the fans a statistical distribution of standing or sitting, screaming or clapping, and different volumes throughout. The physicist could start to approximate the sound that we then hear from some distance. In this sense, the thermal radiation spectra were taunting Planck. Why was the spectrum (the roar) independent of the black-body’s material (the exact stadium, location, and crowd size)? And why did the spectral curve of light from these bodies have exactly one shape and no other? His attraction for the universal pulled him to thermal radiation.
As he entered the problem, Planck would for the first time need to confront light in detail. If there were two things Planck felt he could count on in 1894, they were the second law of thermodynamics and the newly confirmed theory for the propagation of light. The esteemed Heinrich Hertz (who had been offered both of Planck’s jobs before Planck), had published his evidence for electromagnetic waves in 1888, and Planck had started following his work closely.9 “Dear colleague, Sorry to take your time but it’s a quick question,” Planck wrote to Hertz in the summer of 1890. “I read your article ‘Electrodynamics for stationary bodies’ with great delight.” Planck went on to ask if perhaps Hertz had made an error with a minus sign, and hadn’t he made a typo in equation 8? “I really hope I didn’t take too much of your time.” Planck was notorious for this kind of exacting reading, and it helped make him an excellent editor of Annalen der Physik.
He approached the black-body problem in his usual methodical fashion. He began by picturing a hollowed out pocket inside a material—a cavity—just like his old professor Kirchhoff. In 1860, Kirchhoff published his original examination of thermal radiation. He possessed an incredible ability to assimilate vast swaths of information and render an insightful, unifying summary. And he had done so again with the spectral radiation emitted from objects, noting from his own experiments that the ratio of absorbed and emitted light from an object did not depend on the material itself; he coined the term “black body” (as well as “gray body” for the not-quite-perfect black body), and declared that a “universal function” underwrote the thermal radiation.10 (It is still astounding that, at such an early time, Kirchhoff postulated a universal character of thermal radiation, despite inadequate and incomplete experimental evidence to support the notion.)11
Planck in his calculations assumed the cavity was a perfect sphere and had no air in it—the pocket held a perfect vacuum, with no debris or even a single molecule of gas. The entire problem then dealt with the electromagnetic waves (light), inside the cavity and their interaction with the cavity walls. Since the actual material of the walls would not matter—again, mud, chocolate, and metal would behave the exact same way for thermal radiation—Planck used the most generic version of matter. He assumed a series of “resonators” on the inner surface. Though we might be tempted, with modern eyes, to read specific physical meaning into Planck’s resonators, he most probably just sought the simplest possible building block for his theoretical black body.12 He borrowed the notion of an electric resonator from the work of Heinrich Hertz, citing one of Hertz’s papers from some six years prior.13 So while the Hertz resonators had an electrical character, Planck might have shrugged off any question about their real nature. Interestingly, the idea of oscillating molecules giving off radiation had been proposed years earlier (in English, by James Clerk Maxwell), but Planck had probably not seen it.14 Eventually, Planck and others would speculate that the resonators might be electrons, but at the beginning of his work, he wrote of no specific physical meaning for them.
Planck’s resonators each had a characteristic frequency, meaning that each one could interact with one and only one color of light. If we go back to the analogy of a football stadium, Planck was assuming each fan could only absorb and emit one tone. As with many initial models in physics, this assumption is about as realistic for the walls of a cavity as it is for football fans. The aim of Planck’s approach was to model the way these abstract electric resonators took in and then sent out light into the empty pocket. (His first lecture on the topic, to the Prussian Academy of Sciences, was entitled “Absorption and Emission.”) He hoped that the eventual radiant spectrum he computed would simultaneously match observed laboratory measurements and prove that the spectrum maximized the cavity’s entropy, confirming and upholding the second law of thermodynamics.
Through the first several years, he tried to conquer the problem using classical and continuous techniques. His first black-body papers built a framework with few complications, but then slowly increased the model’s complexity, from one paper to the next. He aimed to show that no matter what kind of light might fill the cavity initially, that the activity of the resonators would eventually yield the observed black-body radiation. He wanted to uncover a one-way arrow of physics from any starting point to the final one, so that he could explain how any object would arrive at the same experimental output. But doubts began to encircle him in late 1897.15
“Any unidirectionality which Hr. Planck finds,” Boltzmann wrote in a devastating critique, “must … derive from his choice of unidirectional initial conditions.”16 Boltzmann’s point was that Planck’s attempts to show a universal and unstoppable series of events were not universal at all. Boltzmann correctly detected that Planck’s theory had hidden training wheels. It wasn’t quite ready to balance on its own. Nature clearly could start anywhere and arrive at the same endpoint. But Planck’s theory needed a carefully selected starting point or it tumbled over. A robust theory should not be sensitive to the so-called initial conditions, and every starting point (A, B, or C) should lead to point Z, the black-body spectrum seen in laboratories. After initially disputing Boltzmann’s zinger, Planck conceded the point by the end of the year. He had to try something new.
Planck knew and respected Boltzmann’s work even though he struggled to assess its utility. While Boltzmann embraced probability calculus as a favorite tool, it would have struck most physicists as esoteric, extreme, or even confounding in the 1890s. But by 1898, Planck was warming to Boltzmann’s ideas.17
That year, Planck adopted a more statistical approach to the thermal radiation problem, computing average quantities over the entire spectrum of possible resonator frequencies (and the resulting light colors). He introduced a notion of “natural radiation,” which was the electromagnetic version of Boltzmann’s “molecular disorder” from his first gas theory papers. Planck wrote a true capitulation in 1899, published in a summary article, where he bluntly admitted that Boltzmann and gas theory offered the best path for understanding his sacred entropy and the second law of thermodynamics.18
Meanwhile, something was amiss in Berlin physics laboratories. For a few years, the empirical side of black-body radiation had known relative peace. In 1896, Willy Wien (Planck’s friend and eventual co-editor of Annalen der Physik), had concocted an equation that made a good fit to all black-body data from the labs. Most physicists accepted Wien’s equation as an empirical approximation to the truth, if not the gospel truth. But in 1899, new measurements at longer wavelengths (e.g., looking at infrared light) drifted up and away from Wien’s predictions. Infrared light was shining with unexpected intensity from the hot cavities, so Wien’s equation was clearly not the one used by nature. New experiments pushed further into the infrared, and they arrived on Planck’s Berlin desk every few months in 1899 and 1900. Planck began thinking about a new empirical fit to replace his friend’s. Frustrated by years of trying to build a new theory from scratch, he decided to work backward. If he could intuit the correct equation for nature’s thermal radiation, that would provide a precise compass heading as he navigated the underlying physics.
Turbulence accompanied the weeks leading to his breakthrough. The fall of 1900 witnessed the departure of two German Wilhelms. In August, after labor leader Wilhelm Liebknecht died, the unseen working classes emerged as more than 100,000 choked the streets of Berlin with a solemn funeral march. Even as the Emperor denounced Liebknecht as an enemy of Germany, the march of so-called “iron silence” chilled the city and underscored the vast class divisions of the time. In September, a much closer Wilhelm passed next, as Max’s father died in Munich.
Having paid his respects in Munich, Planck returned to his packed lectures in Berlin. In the weeks following his father’s death, Planck had a flash of insight. Was this back in his Berlin office, during one of his lectures, or even on the train returning from Munich? Whatever the setting, Planck now clearly beheld the mathematical shape nature had been yearning to reveal. The elegant form struck him, and he wrote out a new equation that seemed to avoid the problems of Wien’s earlier guess. On October 19, Max briefly presented his results at a regular meeting of the German Physical Society. He took the floor not with a scheduled talk but with a last minute “discussion remark.”19 His spoken comments consume barely more than two pages. He admits, “I have finally started to construct completely arbitrary expressions for the entropy” of the resonators. When he then writes his result for the audience, he says, “As far as I can see at the moment, [this equation] fits the observational data, published up to now, as satisfactorily as the best equations put forward for the spectrum.”20
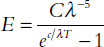
This gives exactly the energy E (and hence the intensity) of radiation one would measure at the wavelength λ for a black body at a temperature T. The big C and little c are just constants that help fine-tune the equation to match the measured data. Such constants are the measurements a physics tailor makes when fitting a body of data with an outfit of mathematics. Planck knew he would have to carry out a real fitting for the values of C and c at some point.
How did his audience react to the unveiling? Presumably, the few interested parties (like the experimenters Pringsheim, Kurlbaum, and Rubens), scribbled this new formula in their notebooks. The following morning, an excited Rubens showed up at Planck’s door holding some pages from his lab. All of his measurements, including the latest in the infrared, fit Planck’s new curve like beads on a string. Rubens was convinced Planck had found it, nature’s thermal voice.
Other colleagues were less convinced. Wien, who heard about the talk from afar, wrote a letter saying he didn’t want to be offensive but that the new equation was surely a significant blunder. Planck replied that he was sure they could resolve their differences and that Wien’s merits in the field would probably be elevated further in time, not diminished. He suggested they meet over the Christmas holidays.21
Meanwhile, Planck was now left with the million-deutsche-mark question: Where did this nice equation come from? His new formula, “had merely the standing of a law disclosed by a lucky intuition,” he wrote later. “On the very day when I formulated this law, I began to devote myself to the task of investing it with a true physical meaning.”22 He set about finding a way to justify the new equation by deriving it from fundamental physical principles. He had to turn his guess into a genuine theoretical idea.
“After a few weeks of the most strenuous work of my life, the darkness lifted and an unexpected vista began to appear.”23 Planck saw that to get his derivation on the right path, he needed to root around in Ludwig Boltzmann’s statistical toolbox. Planck pulled the crucial mathematical pieces from a relatively old paper of Boltzmann’s, 1877’s “On the Relation between the Second Law of Thermodynamics and the Theory of Probability.”24 Boltzmann had enumerated the possible configurations for a bunch of gas molecules using a heavy dose of combinatorics, a type of mathematics examining all the various ways that an array of objects (gas molecules, socks, volleyball players, poker cards, etc.), might be combined. For example, if we have a huge jar of marbles, half red and half blue, and we randomly grab three marbles from it, what are the odds that all three are blue? The answer is approximately one-eighth, or a 12.5% chance. The underlying combinatorics required us to consider all the possible three-marble configurations, such as red-blue-red, blue-blue-red, and so on. There are eight possible combinations and only one gives all blue marbles. Of critical relevance to Planck’s story, combinatorics is a branch of discrete mathematics, with single and separable objects like molecules or marbles. This chunky type of math had no business associating with the continuous light waves arising from a hot cavity, did it? But Max was desperate, and only combinatorics led to his new formula.
In December 1900, he presented his new proof and his new theory. Historically speaking, physicists consider this the proper birth of quantum theory. His audience was reportedly unimpressed, and they struggled to follow Planck through his new forest of mathematics. To obtain his October equation, Max divided allowed resonator energies into parcels. “We consider, however—this is the most essential point of the whole calculation—E [energy] to be composed of a well-defined number of equal parts.”25 Once he could treat the resonator energies like a set of socks, cards, or molecules, he could use Boltzmann’s methods from 1877, and then march in a sensible way to the new black-body equation.
But the new “essential step” was a radical and subversive one, the first time that anyone had considered treating sacrosanct energy in a gritty way. Just as some more progressive physicists had talked about a chunkiness for matter (atoms) and electricity (charges), Planck had quietly submitted a similar granularity for energy. In 1900, he didn’t speak of it as a new type of physics—he didn’t even use the word “quantum.” He said later that this historic step was “a purely formal assumption and I really did not give it much thought except that no matter what the cost, I must bring about a positive result.”26
To imagine Planck’s leap here, consider measuring the heights of children in a large elementary school. We typically measure them on a rough continuum, where children can range easily between, say, three feet and five feet tall. Planck was saying, well, I can describe the heights shown universally by elementary schools all over the world if I just assume children can be exactly three feet high, four feet high, and five feet high, with nothing in between. He didn’t seem to believe this to be the underlying truth, in 1900, but it worked mathematically.
Planck thought he had successfully preserved classical physics and solved the riddle of black-body radiation. He was excited, to be sure, and he could spy success, but there is nothing to suggest he sniffed the fire he had just started. Within 30 years, quantum physics would completely rewrite our view of light and matter, largely from the pens of people like Albert Einstein, Niels Bohr, Werner Heisenberg, and others. Through most of those years, Planck would play the role of a worried parent asking everyone to slow down, to be careful please.
Planck’s derivation itself, we know now, is fundamentally flawed—not in the assumption of granulated energies, but in his argument for their existence. There is no path from classical physics to the exact black-body spectrum. Younger scientists like Einstein and Paul Ehrenfest would be among the first to poke, prod, and criticize Planck’s black-body mathematics, and when Planck eventually returned to the problem, he took a new approach to the derivation. It came to be known as the “second theory” with papers spanning the years 1911–1913. Here, he still hoped to avoid letting the new quantum idea leak into beautiful and continuous light waves. (Interested readers should refer to the appendix, where I give a more modern and proper derivation of the thermal energies radiating from any object, just based on its temperature, and I touch on Planck’s second theory, which launched the concept of “zero-point energy” in the universe.)
The year 1900 would become a retrospective pinnacle for Planck and the new physics. Later, Erwin recalled a late autumn father-and-son garden walk. He said his father quietly announced a breakthrough to his seven-year-old son. Max claimed that his recent work could go down among the greatest discoveries in physics.27 Erwin’s story doesn’t mesh with what we know of Planck’s personality and humility; Erwin could have been shuffling distorted memories of his distant boyhood. But perhaps Max allowed such a grandiose statement for his son’s ears only. Even there, the existing letters show no tendency to boast. There was only one part of his work that could have created such confidence and excitement. In deriving his new formula, he illuminated two fundamental constants, k and h. The former came to be called Boltzmann’s constant, and the latter was known almost immediately as Planck’s constant. While he downplayed the details of his curve’s mathematical derivation, the resulting constants struck Planck as the real breakthrough. He spent the last quarter of his December lecture on their implications.
The unveiling of these fundamental constants, derived purely from Max Planck’s mind combined with the available laboratory data, has only become more impressive with time. The values he unearthed for k and h are within just a few percent of their modern confirmed values. More importantly, he immediately mapped where they would help solve other scientific problems. Planck showed that k was the gateway to calculating exact entropies from a Boltzmann-like statistical framework. In practical and immediate application, Planck deployed k as a type of numeric glue to strengthen the bond between thermodynamics and the field of chemistry. He used k to improve the contemporary values of Loschmidt’s number (the number of molecules in a cubic centimeter of gas), Avagadro’s number (the number of molecules in one “mole” of gas), and the elementary unit of electric charge (the charge on the electron). All of this appears in the last half page of his December 1900 paper. “If the theory is at all correct,” he wrote, “all these relations should be not approximately, but absolutely, valid.”28
Planck’s stance on the constant k would evolve over the years. After Boltzmann’s suicide in 1906, Planck led a group of physicists in calling it “Boltzmann’s constant.” The historian John Heilbron suggests Planck simply made paid homage, an intellectual debt, to Boltzmann.29 However, as the years passed he seemed to regret being short-changed of credit for the monumental breakthrough that k represented. He sometimes wrote of it as “the so-called Boltzmann’s constant,” and he later published a somewhat petulant line. “Boltzmann never introduced this constant, nor, to the best of my knowledge, did he ever think of investigating its numerical value.”30
And though he made fewer calculations with his own constant h in 1900, it has proved every bit as important to physics. As Einstein wrote shortly after Planck’s death, without h, “it would not have been possible to establish a workable theory of atoms and molecules and the energetic processes which govern their transformations.”31
Planck summarized his derivation in a 1901 Annalen der Physik paper, but then turned away from black-body radiation for nearly a decade. He considered the black-body issue resolved, aside from watching the new lab results continue to fit his curve. Otherwise, he turned most of his attention to studying the dispersion of light rays from an object’s surface—this was more a study of reflection than black-body emission. Here, he could tinker with new ideas from Hendrik Lorentz in which tiny, identical “electrons” were said to permeate solid matter.
And if he did expect fame from his black-body success, as he allegedly said to Erwin, he must have been frustrated in the years that followed. From 1901 to 1904, only a handful of other authors referenced his work, noting that his equation fit the available data but saying little else.32 In the early twentieth century, physics was full of more inviting topics than black-body radiation, and besides, Planck had relied on the unpopular ideas of the unpopular Boltzmann.33 The first substantial action on Planck’s breakthrough came in 1905 from the mind of Einstein, but Planck considered that work a bit of wrong-headed excess from an overly exuberant kid. Planck and his colleagues largely ignored the young interloper’s suggestion of “light quanta” (what we now call photons).
It was that year that Planck and Marie moved their family to the suburb of Grunewald, just as he began to review Einstein’s string of five seminal papers. Einstein’s very first annus mirabilis paper concerned a strange experimental observation called the “photoelectric effect.” Others had noted that shining ultraviolet light onto a piece of metal created a spark—what we would now call an ejection of electrons. This effect powers the photovoltaic materials in solar panels. Classical theories, using light as a wave, could attempt to explain this phenomenon—the waves must surely “shake loose” the electrons, or something like that—but they came up short.
Einstein found a way to explain the effect with just one assumption added to Planck’s 1900 paper, but it was radical, even ridiculous to some. He asked, what if light itself literally appears in chunks of energy, measured in scoops of Planck’s new constant h? If light comes in little bundles, then the photoelectric effect would make perfect sense. As little energy bundles hit a metallic surface, billiard-like collisions between the light quanta and the electrons would ensue. Einstein’s model involved just a simple bit of algebra and explained the observed experiments flawlessly.
By proposing such a mechanism for light, Einstein knowingly picked at a painful scab for physicists. The debate about the nature of light had consumed most of the last 200 years, with the wave picture triumphing over the particle picture by the late nineteenth century. Most physicists, especially most established physicists like Planck, had no will to revisit the debate.
In fact Planck’s reaction to Einstein’s idea of an “energy quantum” for light is intriguing. While he embraced and even championed Einstein’s special relativity immediately, he thought the very same genius had made a brash rookie mistake when it came to the photoelectric effect. It was out of character for Planck to ignore evidence this strong and to dismiss an idea so simple and logical. But this was his intellectual turf. Special relativity confronted years of frustrated work from the Dutch physicist Hendrik Lorentz and the French polymath Henri Poincaré (who were both very skeptical of Einstein’s relativity for the rest of their days). But this idea for the photoelectric effect poked its quantized nose into Planck’s business. As flexible as Planck had been in his science, he remained skeptical of light quanta for years to come. In 1913, while writing the otherwise glowing justification of Einstein’s Berlin job offer, Planck couldn’t help himself: “That he [Einstein] might sometimes have overshot the target in his speculations, as for example in his light quantum hypothesis, should not be counted against him too much.”34 Thirteen years after his breakthrough, Planck still wanted to confine his own quantum idea—he drew a line in the physics sand, maintaining that light didn’t fly about in little packets, and energy was not atomized, as Einstein suggested.
To return to our school children analogy, Einstein surveys Planck’s work and says, “In this strange world, you’ve made more than a clever mathematical step. I think you’ve stumbled onto something—the children’s heights really are exact increments of one foot!” Planck would insist, by stages, that it was some localized circumstance that occurred when the children interacted with yardsticks or when the children misreported their own heights to the teachers. Along with many other physicists, it would take Planck nearly 20 years to truly accept that, indeed, the children of the quantum world only come in heights of three feet, four feet, and so on. Einstein knew it was a radical, even disturbing step. “It was as if the ground had been pulled out from under one,” he wrote later.35
Although shocking in retrospect, the word “relativity” was nowhere to be found in Einstein’s 1921 Nobel Prize, “for his discovery of the law of the photoelectric effect.” Relativity was too controversial, mathematical, and theoretical for the Nobel committee, even after its great verification in the eclipse of 1919. Like Planck, Einstein had accumulated an embarrassing number of nominations before receiving the Nobel committee’s approval. After the previous Nobel Prize in Physics went to a man who had designed better measuring rods, an Einstein-sympathetic physicist named Carl Wilhelm Oseen joined the Nobel committee. He quickly grasped the committee’s anti-mathematical vibe and never mentioned Einstein’s relativity work. Instead he wrote persuasively about the link between Einstein’s photoelectric effect “law”—he avoided the word “theory”—and successful laboratory results.36 Since the photoelectric effect could be observed with easy measurements, since it was useful, and since Einstein only needed a bit of algebra to correlate the color of incoming light and the energy of the liberated electrons, this made for award-worthy work.
Even when Planck later came to accept Einstein’s hypothesis, and the existence of photons were confirmed in the early 1920s, he still had to keep his own diction: h would always be a quantum of action, instead of Einstein’s quantum of energy. “My futile attempts to fit the elementary quantum of action somehow into the classical theory continued for a number of years, and they cost me a great deal of effort,” he wrote later. “Many of my colleagues saw in this something bordering on a tragedy.”37
Some authors have attempted to discern exactly what Planck was thinking in 1900, and a few, including the science historian Thomas Kuhn, doubt whether Planck even deserves credit for the birth of quantum theory. And although Einstein never wavered from crediting Planck exclusively for quantum theory, some wonder if Einstein himself might deserve the greatest share of credit for the quantum era.38 Still others argue that asking what Planck knew of true quanta presents a question without meaning for 1900.39 The more appropriate journey might be, as Clayton Gearheart puts it, “to understand Planck on his own terms.” Gearheart has presented a thorough overview of Planck’s utterances and all subsequent analyses of his thoughts, but in the end, he notes a striking silence from Planck on interpreting his “energy elements.”40 He was clearly uncomfortable crawling onto a shaky limb of conjecture, and he stated plainly (as in his 1906 book on the topic), that his work left a dire need for physical interpretation. In the end, those who credit him with full understanding in 1900, as many physics textbooks do, are oversimplifying the real story of a discovery, and those who would claim he possessed no comprehension of his innovation also paint with too crude a brush. In this sense, the lucid analysis set out by the science historian Martin Klein in 1962 still rings true.41 Planck knew he needed energy elements and the combinatorics that came with them to correctly derive the new black-body radiation law, and he knew this was a step that, at best, would never fit comfortably within the established physics that came before. Physicist and former Planck student James Franck recalled a Planck talk within a few years of his discovery. “He spoke of some of his attempts to avoid the quantum hypothesis if possible. His conclusions, however, were the following: There is no way out … we shall see that it will penetrate into more and more fields of our physics.”42
Planck’s evolution on quantum theory moved slowly—he was usually very cautious when it came to the meaning of his h, at least in public and in print. One of the only surviving versions of him thinking off the record is preserved in the letter diaries he maintained with his college friends. In early 1908, he responded directly to a question from Carl Runge.
Regarding Carl’s question about my ideas regarding the elementary quantum, I must first confess that at present they are still pretty poor, but I would like to say the following. … the elementary quantum[’s] full explanation cannot be done by considering a state, but only by considering a process. In other words: We are not concerned here with a theory of atomism in space, but with an atomism in time, via processes we usually think of as continuous in time, that have, in fact, temporal discontinuities. That the laws of ordinary mechanics and electrodynamics, which always presuppose temporal continuity, are inadequate here, may well be considered certain.43
In other words, while professing public caution for many years to come, the more private and internal Planck considered quantizing time itself. He even proposed, in the same 1908 entry, that this might relate to Einstein and Minkowski’s spacetime. As of 2014, quantized spacetime has not been proved, but it plays a key role in the efforts to unite Einstein’s relativity with quantum theory. Quantized spacetime would mean the fabric of the cosmos has granularity, a grit, as opposed to being absolutely smooth and continuous. In 1908, Planck’s notion was many years ahead of anyone else proposing the idea formally.44 The diary entry also underscores the extent to which Planck knew what was up: He had served quantum poison to “ordinary mechanics and electrodynamics,” so classical physics was as good as dead.
Hendrik Lorentz probably made the first dent in Planck’s public reluctance to discuss the end of classical physics, even where Einstein had failed. This came just two months after the 1908 diary entry, amidst a public talk delivered in Rome. There, Lorentz made it clear that Planck’s law didn’t belong with classical theory. Another equation showed the best link to classical ideas; it was the so-called Rayleigh-Jeans law. It completely failed to fit the data, but its derivation was more legitimate and traditional than Planck’s, and Lorentz said so.45 He considered Planck’s success “exceedingly curious.” By then, several authors had found gaps in Planck’s attempts to explain his equation: Lorentz, Jeans, Ehrenfest, and Einstein had all noted quirky, flawed steps as Planck contorted to make his equation fit with traditional physics. Or as Lord Rayleigh stated, some found the derivation impossible to follow.46
Planck replied to Lorentz’s Rome talk and made his first written concession that something funny was happening with the resonators. When they absorbed or emitted light, his strange new constant h reared up and quantized the exchange of energy between matter and light. But he refused to see light itself as quantized. The 1908 Lorentz Rome lecture was personally crushing to Planck. He heard an international authority—someone he saw as a Clausius-like figure, a nearly flawless elder—cast doubt on his work. And the criticism emerged when the Nobel selection committee was finalizing their options for the year. They initially voted, privately, for Planck to win the Physics prize.47 Rumors circulated throughout Berlin and even in the popular press that Planck would soon be recognized for his 1900 discovery. Although his equation still fit the data perfectly, most physicists failed to agree on its meaning, and the Nobel Prize committee got nervous enough to reconsider. The 1908 Nobel Prize in Physics went instead to Gabriel Lipmann for discovering color photography.
Meanwhile, Einstein was just as frustrated. Only a few younger physicists embraced his notion of bundled light. His friend and colleague Paul Ehrenfest accepted the truth as early as 1906. And in the summer of that year, Einstein received a letter from Max Laue (who became von Laue in 1913). He apologized to the young Einstein for a slow response, complaining of military service and other obligations. But Laue then wrote that with respect to quantized light, “I have no objections to make.” But wasn’t he Planck’s own assistant? “I have never discussed [this] with my boss. It is possible that there are differences of opinion between him and me on this question.”48
Outside of Ehrenfest and Laue, Einstein found few sympathizers. Undeterred, as always, Einstein used quantum ideas to stunning effect again in 1907, writing a groundbreaking paper on thermal physics at very cold temperatures.49 As new cooling techniques opened ever lower temperatures to laboratory exploration, certain material properties changed sharply. Einstein solved one of the open riddles (the strange drop in a material’s so-called specific heat value), using the granular energies of quantum theory. This work raised a few extra eyebrows.
In 1908, Lorentz began to accept that something was truly amiss with classical notions of light and energy, just in time for his Rome talk. Willy Wien and Planck began to join them circa 1909, to a limited extent. And in 1910, a few others changed their minds, including the chemist Walther Nernst: “I consider the quantum theory certain.”50
The watershed moment for quantum theory’s childhood arrived in 1911. The Belgian chemist (turned businessman, turned philanthropist), Ernest Solvay underwrote the first conference dedicated to “The Theory of Radiation and the Quanta.” This and the subsequent quantum theory meetings were known as the Solvay Conferences. Gathering at the Hotel Metropole in Brussels, 18 leading physicists sifted through the broken shards of classical theories of energy and light. Einstein, at 32, was the youngest, and he began the conference with a clear call to arms, starting with his updated work on specific heats. But the old guard bombarded him with challenges. Poincaré, Lorentz, and Planck led the way in voicing doubts.51 They didn’t want to toss out the good classical baby of electromagnetic waves with the quantum bathwater. Einstein found the experience frustrating and even depressing. He wrote to a friend that the meeting felt to him like, “a lamentation on the ruins of Jerusalem.”52 And about Planck in particular, Einstein wrote that the esteemed professor was “stubbornly attached to preconceived opinions that are undoubtedly false.”53
As Planck wrote afterward, older, established scientists were duty-bound to convey “an increased caution and reticence in entering into new paths.”54 From his point of view, he had already shifted his thinking a great deal. He found the meeting extremely tiring, but he would look back on that week, with conversations varying from exasperated to breathless, as one of the peaks in a long career.55
A year later, Planck’s second edition of The Theory of Heat Radiation gave an interesting window into the awkward childhood of quantum theory and his ongoing worries. In the preface he wrote that his ideas on black-body radiation “have met with little general acceptance.” He painted himself as the reasonable pioneer caught between two camps: those who, “through conservatism, reject the ideas,” and a few others who, “have felt compelled to supplement [my ideas] by assumptions of a still more radical nature, for example, by the assumption that any radiant energy whatever, even though it travels freely in a vacuum, consists of indivisible quanta or cells.” He admitted that his first edition, from 1906, was deficient. But he rejected the notion that such elements were relevant to anything but the interface between matter and light; Einstein went too far for Planck, even well after the Solvay conference. “Since nothing probably is a greater drawback to the successful development of a new hypothesis than overstepping its boundaries, I have always stood for making as close a connection between the hypothesis of quanta and the classical dynamics as possible.”56
So in 1944, when Planck’s remaining colleagues crawled through rubble, brushed the dust from their tuxedos, and insisted on toasting his career, they celebrated a story of Max the way-shower. They lauded a revolutionary who brought quantum to the world, even if he had only reluctantly played along after his first inspiration. Certainly, during the speeches of that evening, they noted his prolific ways. In a scientific era predating our current obsession with fire-hose–like research output, Planck published an array of books, 42 notable papers in Annalen der Physik spanning six decades of work, and just as many articles in other outlets. They would have mentioned the impressive expanse of his physics gaze, with key publications as far flung as thermal physics, fluid dynamics, and relativity theory.57 His colleagues might have mentioned his philosophical battles and victories versus the positivists, those who would constrain human imagination. The assembled had to toast his great successes as a leader and administrator of German physics and a spokesman for German science in the face of absurd challenges. But in the end, the crowning achievement of their Geheimrat Professor Planck would always be conceiving quantum theory. After accumulating 75 Nobel nominations over more than 20 years, he finally won the 1918 prize in 1919, for “his discovery of the energy quanta.”58
Looking back from a century’s remove, we can try to set out Planck’s most lasting contributions. His igniting quantum theory leads the list, but it would be a sad mistake to stop there. He also elevated the concept of entropy, gave the world the notion of natural units, and discovered the ubiquitous “zero-point” energy.
Planck’s focus on entropy (and the closely associated idea of irreversibility) was far ahead of its time. It is no exaggeration to say he took a rough hewn entropy notion from Clausius, like a shapeless piece of flint, and carved it not just into a useful blade but a Swiss-army knife. Thanks largely to Planck, entropy became quantifiable, statistical, and useful. Today, an enormous range of scientific studies employ entropy as a tool, including something as extreme as black hole thermodynamics, where the size of the hole’s boundary makes a nice analogy to its entropy,59 or something as practical as information theory, where the basic measure of information is its “Shannon entropy.” And in repositioning entropy in the second law of thermodynamics, suggesting that it always tends to increase, Planck underlined the so-called arrow of time. That the universe moves irreversibly in one direction is accepted, yet still mysterious. Some leading physicists suggest we might be well served by focusing more of our attention here, despite thousands of years of head-scratching.60
Although Planck was humble about his early thermodynamics work, his contributions here should not be overlooked. Science historian Dieter Hoffmann argues that Planck, stripped of his black-body work, would still be famous today for his pioneering work in thermodynamics. If one takes citations as the ultimate measure of a scientific author’s impact, the data underscore Hoffmann’s claim. The two most-often cited of Planck’s papers come from his early work, linking entropy to the behavior of chemical solutions.61 And Planck had kept contributing to thermodynamics. In 1911, the same year as the Solvay conference, he had put the third law of thermodynamics into its most palatable form: As the temperature of an object approaches absolute zero, so too will its value of entropy.
Planck also suggested natural units in the last breaths of the nineteenth century. And when he then gave the world h and k, he recognized an extraordinary opportunity. “With their help we have the possibility of establishing units of length, time, mass and temperature, which necessarily retain their significance for all cultures, even unearthly and nonhuman ones.”62 Every universal constant has units. The speed of light c, for instance, sensibly measures distance (meters) divided by time (seconds). In the case of h, the units are energy multiplied by time. It’s not always pretty—the universal constant of gravitation, G, has units of distance cubed, divided by both mass and time squared. But combinations of the various fundamental constants can provide absolute measures of time, space, energy, and so forth. Hence we have, for instance, the Planck time and the Planck length—they give a voice to the universe in its own terms. Independent of human bias, they have proved a boon to the further development of theoretical physics, in terms of both new perspectives and also the subsequent versions of the natural units. (They provide a kind of style manual for all physicists who do their work with pencil, paper, and laptop.)
And finally, any list of Planck’s contributions would be incomplete without the mysterious notion of a zero-point energy. In his second approach to deriving his radiation law, his slightly modified mathematics meant that, even if an object had a temperature of absolute zero, there would still be some sort of energy remaining in it. Though that seemed an oddity at the time, a necessary but inconvenient mathematical bit of detritus, the idea has only grown in importance over the last 100 years. The now-accepted idea that space itself has a seething and invisible lake of energy in it, even without particles or light involved, has implications for the structure of the universe itself.63 The zero-point energy of the cosmos is automatically a candidate for determining the source of “dark energy” that appears to push the boundaries of the universe outward with ever greater speed. The dark energy is still mysterious as of this writing, and it is not properly accounted for by any computation of zero-point energy, but the two often appear in the same conversations. And since any discussion of dark energy is tied to an idea that Einstein originally launched as a “cosmological constant,” it is accurate to say that Einstein and Planck debate one another intensely even today, as quantum theory and general relativity still confront one another. Like their authors once did, the two theories may even need one another, despite the appearance of irreconcilable differences.
In a joint 1932 interview, both men underlined an irrational faith in the universe as a scientific necessity. “As Einstein has said, you could not be a scientist if you did not know that the external world existed in reality,” Planck said. “But that knowledge is not gained by any process of reasoning. It is a direct perception and therefore in its nature akin to what we call Faith. It is a metaphysical belief.”64 In that interview, as an exemplar of this Faith, Planck noted the scientist Johannes Kepler—300 years his senior—with a tone of ultimate respect, even awe.
He was always hard up. He had to suffer disillusion after disillusion and even had to beg for the payment of the arrears of his salary by the Reichstag in Regensburg. He had to undergo the agony of having to defend his own mother against a public indictment of witchcraft. But … what rendered him so energetic and tireless and productive was the profound faith he had in his own science, not the belief that he could eventually arrive at an arithmetical synthesis of his astronomical observations, but rather the profound faith in the existence of a definite plan behind the whole of creation. It was because he believed in that plan that his labour was felt by him to be worth while and … by never allowing his faith to lag, his work enlivened and enlightened his dreary life.65
Kepler makes a compelling analogue for Planck, and not just as Germans or even as scientists overcoming incredible personal hardship. Working in the seventeenth century, Kepler took a set of data that defied all reasonable description—the detailed nightly positions of the planets in the sky—and found the perfect equations to describe these measurements. When looking at enormous compilations of planetary positions, he began to see a mathematical pattern and with his new laws of planetary motion, he solved a fundamental riddle: the structure of the solar system. Kepler’s laws of planetary motion apply equally well to other star systems as well; they are as universal as Planck’s law of thermal radiation. After trying several ill-fated mathematical approaches to explain an exhaustive list of planetary positions, he finally began to see ellipses in them. Mathematics had always been Kepler’s chief tool; childhood smallpox had left his hands and eyes deficient for using telescopes or lab instruments.66 In a real sense then, as Kepler didn’t collect measurements himself, he was a true predecessor of Planck and one of the first mathematical physicists. Just as Kepler had an astonishing ability to see the mathematical form in confounding planetary data, Planck had the same when looking at the black-body radiation curves. While Kepler would not live to see his name immortalized, Planck did live to enjoy recognition and the toasts of colleagues.
For a night so bomb-free that Heisenberg called it “spooky,” surviving Berlin colleagues recalled the superlative decades of their Max Planck. He held an almost religious significance for them. According to the journalist James Murphy, whether you spoke with Planck about science or anything else, “one often feels that this tragedy of his children has made a deep impress on his soul. The memory of it seems to evoke a certain wistful quality which is profound in his nature and give it the warmer glow that one is inclined to call mystic.”67
This mystic of German science would have endured his painful back with unusual ease that night. His spirits lifted with so many friends and memories so close. As the guests dispersed, he would have stood with Erwin. Did they embrace as they said their good nights? Max probably suggested another Rogätz meet up, whenever Erwin and Nelly could visit again. But the banquet’s end marked the last time Max would see and touch his son before the Gestapo stepped between them.