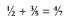3
EVERYBODY COUNTS
THE NUMBER SENSE built into newborn babies is similar to that observed in rats, chimpanzees, and monkeys. In fact, Mark Hauser of Harvard University and his colleagues have carried out Karen Wynn’s original experiments with rhesus monkeys, obtaining similar results. But among all the animal species, only humans seem able to take this deeply ingrained but strictly limited ability and extend it to the point where we can quantify and talk about collections ranging into the billions. Do we in fact extend our basic, built-in number sense, or do these larger collections call on an entirely different mental ability?
Certainly our brains appear to handle collections of three or fewer members differently from the way we deal with larger collections. In experiments where adult subjects are asked to name the number of dots randomly arranged on a slide shown to them, the time required to give an answer is almost identical for one and two dots, and only slightly longer for three (just over half a second). Beyond three, however, the time starts to increase rapidly. As the number of dots grows, so too does the number of errors.
The sudden change in behavior beyond three objects suggests that the brain may be using two different mechanisms. For collections of three or fewer objects, recognition of numerosity appears to be virtually instantaneous, and achieved without counting. For collections of four or more objects, however, it is at least plausible that the result is obtained by counting. The time required to give the number of objects in the collection increases linearly as the number goes up from three to six. This is exactly what you would expect if the answer was arrived at by counting.
Further confirmation that the brain generally handles collections of three or fewer by an “all at once,” instinctive (and subconscious) process comes from studies of patients with certain cerebral lesions. Although brain damage often affects large parts of the brain, destroying many mental faculties, sometimes a lesion is very local and has just one or two very specific effects. Patients with such “focused” lesions provide cognitive psychologists with extremely useful evidence they would otherwise be unable to obtain. In one case, described by Dehaene in The Number Sense, a patient in Paris suffered a brain lesion that destroyed her ability to count, or even to check off objects one after another. Yet when three or fewer dots were flashed onto a computer screen, she could immediately report the correct number of dots.
But even if we use a different mechanism to arrive at the numerosity of collections of more than three members, the human concept of number is almost certainly built upon our innate sense of number as being a property of collections of discrete physical objects. For instance, if you show a three- or four-year-old child two red apples and three yellow bananas and ask her how many different colors there are or how many different kinds of fruit she can see, she will answer “five.” The correct answer is two, of course. But so deeply ingrained is the idea that number is a property of collections of discrete physical objects that it takes the relative sophistication of five years’ experience in the world before a child can overcome that built-in notion and apply numbers in a more abstract fashion.
What happens when we are faced with a collection of considerably more than three objects? Are we able to estimate how many there are? Can we distinguish between two collections having different numbers of members?
Certainly we know that if we are asked to give the exact number of objects in a collection having, say, ten or more members, our only strategy is to count them, either one by one or perhaps two by two or even three by three. But what if we just want a reasonably good estimate? How good are adult humans at estimating the number of objects in a collection of, say, a hundred?
The experimental evidence shows that we are better than you might think, although we can be misled by surrounding circumstances. For example, when asked to estimate the number of dots on a page, subjects will typically underestimate the total if the dots are placed irregularly and overestimate if they are in a regular pattern. Again, if shown twenty-five or thirty dots on a page, we will overestimate the total if the collection is surrounded by a border of hundreds of other dots and underestimate if the border contains just ten or twenty dots.
When not misled by surrounding circumstances, however, we do seem capable of providing good estimates of collection sizes, and people who regularly need to estimate say, large crowds of people can become quite good at it. Moreover, our ability increases with just a small amount of mental priming. For instance, if we are first shown a collection that we know contains, say, 200 dots, we can provide pretty good estimates of collections of between 10 and 400 dots.
Easier than estimating the total is spotting that two collections have different sizes. Here a distance effect comes into play. It is much easier to distinguish the sizes of collections where the difference between them is significant compared to the totals than when the difference is relatively small. For example, we can generally tell that collections of, say, 80 and 100 objects have different sizes, but are unable to spot the larger of two collections of 80 and 85 objects. In fact, our ability to distinguish collection sizes is described by a remarkably precise numerical law, called “Weber’s law” after the German psychologist who discovered it. If a subject can discriminate, say, a set of 13 dots from a reference set of 10 dots with a success rate of 90 percent, then the same subject will be able to discriminate 26 dots from a reference set of 20 with the same degree of accuracy. As long as the ratio of the test set to the reference set is held constant, the subject’s success rate will remain constant as well. It’s as precise a linear relationship as you are likely to find in psychology!
The Weber effect has also been observed in monkeys. David Washburn and Duane Rumbaugh tested two monkeys, Abel and Baker, who had previously been taught the numerals o to 9—in the sense that they could associate the numeral with a collection of objects having that many members. The monkeys were trained to use a computer joystick to select one of a pair of numerals presented on the computer screen. They were rewarded with as many small pellets of food as the number they had selected, thereby encouraging them to select the larger number. After a training period, Washburn and Rumbaugh measured their performance. The further apart the two numbers, the faster was their response time and the greater their accuracy.
So there is some similarity between monkeys and humans, but not much. When it comes to estimating sizes of collections and detecting differences in collection sizes, adult humans are uniquely able to extend the number sense far beyond 3.
Moreover, humans can do much more than that. In addition to our innate number sense, which gives us reasonably good estimates of the sizes of collections, we have counting, which gives us exact totals. We also have arithmetic, which gives us precise numerical answers to a whole range of questions. Where did these unique features come from? Were we born with these abilities or are they skills we learn?
THE COUNTER CULTURE
Two keys unlock the door to the numerical world beyond 3, and as far as we know, only our species has ever found either one. The first is the ability to count. The second is the use of arbitrary symbols to denote numbers and thus manipulate numbers by the (linguistic!) manipulation of those symbols. These two attributes enable us to take the first step from an innate number sense to the vast and powerful world of mathematics. Both abilities, counting and symbolic representation, are among the collection of (related) abilities that our ancestors acquired between 75,000 and 200,000 years ago, as we shall discover in Chapter 8.
Counting is not the same as saying how many members are in a collection. The number of members in a collection is just a fact about that collection. Counting those members, on the other hand, is a process that involves ordering the collection in some fashion and then going through it in that order, counting off the members one by one. (I shall ignore variations where the collection is counted by twos or threes. Those are just that: variations.) Since counting does in fact tell us the number of members in a collection, we often confuse the two. But that is a consequence of familiarity. Very young children view counting and number as quite unconnected. Ask a three-year-old to count up his toys and he will perform flawlessly: “One, two, three, four, five, six, seven.” He may well point to each toy in turn as he counts. But now ask him how many toys he has, and chances are he will tell you the first number that pops into his head—which may not be seven. At that age, children simply do not relate the process of counting to that of answering the question “How many?”
Incidentally, even though a three-year-old will probably not know how many objects make “three,” a two-and-a-half-year-old does realize that number words are different from other adjectives. For instance, suppose you show a two-and-a-half-year-old a picture of a single red sheep and another of three or four blue sheep. If you say “Show me the red sheep,” the child will point to the red sheep. Say “Show me the three sheep” and the child will point to the picture of the blue sheep. The latter may have three or four sheep; the child does not appear to know exactly what number “three” is. But she does know that “three” applies to a collection of objects, not to a single object. She also knows that it is okay to say “three little sheep” but not say “little three sheep.” In short, by age two and a half, children realize that number words are different from other words.
It is around the age of four that children realize that counting provides a means to discover “How many?” Part of that realization must be the recognition that, when you are counting the members of a collection, the order in which you count doesn’t matter. Regardless of which object is “first,” “second,” and so on, the number you finally reach is always the same. With this remarkable insight, which we all simply take for granted, we enter the counter culture.
My use of the word “culture” just then was more than a cute pun. There are a few cultures today that do not have counting (at least, they do not have counting beyond two, which arguably means they don’t have counting at all). In the past there were many more. Most likely our ancestors did not have counting either. Particularly suggestive evidence is that the words we use for the first three numbers—the ones that correspond to our innate number sense—are very different from all the others.
For example, starting with four, there is a simple rule for turning the number word into the corresponding adjective for use in an ordered list: add the suffix “th” (and possibly make some minor change to facilitate pronunciation). Thus, “four” becomes “fourth”, “five” becomes “fifth”, “six” becomes “sixth”, and so forth. For the first three numbers, however, there are completely different words for the ordinals: “first”, “second”, and “third”. Moreover, these words have other, related uses. “Second” can be used as a verb, meaning “to support”, and we have the adjective “secondary”. The Indo-European root of the word “three” is related to the Latin prefix trans (meaning beyond), the French word trés (meaning very), the Italian troppo (meaning too much), and the English through, all of which suggests that it was once the largest numeral.
The other European languages likewise show special treatment of the first two numbers followed by a more regular form for all the others. In French we have: un/premier, deux/second (or deuxième), and then the more regular troisltroisième, quatre/quatrième, etc. In German we find: ein/erst, zwei/zweite (or ander), and then drei/dritte, vier/vierte, etc. In Italian: uno/primo, duelsecondo, and then tre/terzo, quattro/quarto, etc.
Further, we have special ways to talk about collections of two or three objects. For two, we speak of a pair, a brace, a yoke, a couple, or a duo, and we have the adjective “double.” For three, we have the words “triple,” “trio,” and “treble,” Beyond three, however, we make use of the regularly constructed forms “quartet,” “quintet,” “sextet,” etc. Many of the words for a collection of two objects are restricted to certain kinds of objects, consistent with the idea that the innate numbers one, two, and three are intimately connected with collections of physical objects. Thus, for example, we speak of a brace of pheasants, a yoke of oxen, and a pair of shoes, but cannot talk about a “brace of shoes” or a “yoke of pheasants.”
How and when did our ancestors first develop the idea of counting, as opposed to estimating using their innate number sense? Quite possibly they started out dealing with collections the way the Aboriginal tribe the Warlpiris do today, by considering just three possibilities: one, two, and many, with three being the point where exact counting ends and the collection is simply “large.”
But how did our ancestors learn to count beyond three?
Perhaps they began the way young children do today. As any parent or elementary school teacher knows, children learning arithmetic spontaneously use their fingers. Indeed, so strong is the urge to count on their fingers that if a parent or teacher tries to insist that the child do it the “right” or “grown-up” way, the child will simply use her fingers surreptitiously. As for the idea that dispensing with fingers is the “adult” way, many adults also do arithmetic with their fingers.
Certainly, our base-10 number system is evidence that counting began as finger-enumeration. Since we have ten fingers, if we use our fingers to count, we run out of counters when we reach ten, and we have to find some way of recording that fact (perhaps by moving a pebble with our foot) and then starting again. In other words, finger (and thumb) arithmetic is base-10 arithmetic, where we “carry” when we reach ten. (The satirist and mathematician Tom Lehrer once quipped that base 8 is just the same as base 10 “if you’re missing two fingers.”)
Further evidence in favor of the hypothesis that arithmetic began with finger manipulation is our use of the Latin word digit to mean both fznger and numeral.
Admittedly, neither piece of evidence is overwhelming, but they are suggestive. The same can be said for my next piece of evidence, this time from the neuroscience laboratory.
By various techniques scientists are able to measure the level of activity in different parts of the brain while it is engaged in a particular task. For instance, the massive frontal lobe is where most brain activity takes place when a person is using language. In a sense, the frontal lobe is the brain’s “language center.”
1When a typical person is performing arithmetic, the most intense brain activity is in the left parietal lobe, the part of the brain that lies behind the frontal lobe. Now, as it happens, similar studies have shown that the left parietal lobe is also the region that controls the fingers. (It requires a considerable amount of brain power to provide the versatility and coordination of our fingers, and hence a large part of the brain is devoted to that task.)
The question leaps to the mind at once: is it a coincidence that the part of the brain we use for counting is the very part that controls our fingers? Or is it a consequence of the fact that counting began (with our early ancestors) as finger-enumeration, and that over time, the human brain acquired the ability to “disconnect” the fingers and do the counting without physically manipulating them?
Clinical psychologists have also found a connection between finger control and numerical ability. Patients who sustain damage to the left parietal lobe often exhibit Gerstmann’s syndrome, a lack of awareness of individual fingers. For instance, if you touch one finger of a typical sufferer of Gerstmann’s syndrome, the individual cannot say which finger you touched. These people are also typically unable to distinguish left from right. More interestingly, from our point of view, people with Gerstmann’s syndrome invariably have difficulty with numbers. For example, both Frau Huber and Signora Gaddi, the individuals having no number sense whom we met in the previous chapter, suffered from Gerstmann’s syndrome.
It is tempting, to say the least, to speculate as to the reason for the correlations between Gerstmann’s syndrome, finger control, and numerical ability. If early Homo sapiens’ first entry to the world of numbers was via their fingers, then the large region of the brain that controls the fingers would be the one in which their descendants’ more abstract mental arithmetic would be located. Very likely, our present-day, strictly mental number sense is an abstraction from our ancestors’ physical finger manipulations. Mental arithmetic may be in essence “off-line” finger manipulation, which became possible when the human brain became able to disconnect the brain processes associated with finger manipulation from the muscles that control the fingers.
It’s a possibility. An alternative early means of counting—which could have co-existed with finger counting—was to use some sort of physical tally system such as making notches on a stick or a bone. Notched bones have been discovered that date back at least 35,000 years. Thus, our ancestors may have used a physical enumeration system as much as 40,000 years ago, the time when, according to the fossil record, humans started to use symbolic representations in cave paintings and rock carvings.
Of course, use of fingers or tallies indicates a conception of numerosity, but does not necessarily imply a concept of number, which is purely abstract. Abstract numbers are the key to modern mathematics. How and when did we acquire them? The best current evidence we have for the introduction of abstract counting numbers, as opposed to markings, was discovered by the University of Texas archaeologist Denise Schmandt-Besserat in the 1970s and 80s. At archaeological sites in Iraq, where a highly advanced Sumerian society flourished from around 8000 to 3000 BC, Schmandt-Besserat kept finding small clay tokens of different shapes, including spheres, disks, cones, tetrahedra, ovoids, cylinders, triangles, and rectangles. The older ones were simple, later ones often quite intricate. Gradually, as she and other archaeologists slowly pieced together a coherent picture of Sumerian civilization, Schmandt-Besserat realized that the puzzling clay tokens were counters used to support commerce. Each shape represented a certain quantity of a particular item—metal, a jar of oil, a loaf of bread, and so on.
The first tokens appeared around 8000 BC. By around 6000 BC they had spread throughout the Fertile Crescent, which stretched from present-day Iran to Syria. Over the years, even more elaborate shapes were produced, including parabolas, rhomboids, and bent coils, and some of the tokens began to carry markings.
Two ways were developed to keep a complete record of a man’s possessions. The more elaborate markers were strung like beads across an oblong clay frame. The simpler tokens were wrapped in a flat sheet of wet clay, which was then sealed and allowed to harden into a spherical envelope. Both methods were fully functional early forerunners of our present-day bank accounts. But the clay envelopes had an obvious drawback. Whenever someone wanted to trade, or even check the status of his account, the envelope had to be broken and a fresh one made. To reduce the frequency of envelope breaking, the Sumerians hit upon the idea of impressing on the wet clay of the envelope each token that was to be enclosed, prior to the envelope being sealed. That way, the outer surface of the envelope carried an indelible record of what was inside.
In time the Sumerians realized that with these visible records on the outer surface of the envelope, the contents were unnecessary. The imprints of clay tokens could represent possessions. So the Sumerians stopped sealing the tokens in clay envelopes and instead simply impressed the tokens onto a flat tablet of wet clay.
The step from impressed clay envelope containing tokens to impressed clay tablet is the first known use of abstract markings to denote counting numbers. In fact, the Sumerian accounting tablets are the earliest known writing system, which means that the use of markings to denote numbers preceded the use of markings to denote words. To put it another way, early Shakespeares obtained the tools of their trade from early Newtons.
Of course, since the Sumerians had different tokens, and correspondingly different markings on the clay tablets, to represent quantities of different kinds of items, they did not really have a single number system. Rather, each kind of item had its own separate number system. But by eliminating the need for physical tokens and using symbolic markings instead, they made the first major step toward the all-purpose, abstract numbers we use today.
SYMBOLS OF SUCCESS
One of the things that makes arithmetic possible—for those who can do it!—is the extremely efficient symbolic notation we have for representing numbers. For the Romans, with their cumbersome notation of Is, Vs, Xs, and so on, even the simplest of arithmetic sums was difficult to calculate. And they had no way to represent fractional or negative quantities.
The number notation we use today is far more efficient. Using just the ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, we can represent any positive whole number. The trick is to use these digits to form numerical “words” that name numbers, just as we put letters together to create words that name various objects or actions in the world. The number denoted by a particular digit in any numerical “word” depends on its position in that word. Thus, in the number
the first digit 1 denotes the number
one-thousand, the second digit 4 denotes
four-hundred, the third digit 9 denotes
nine-tens (or ninety), and the last digit 2 denotes the number
two. The entire “word” 1492 denotes the number:
one-thousand and four-hundred and nine-ty two
Our present number system was developed over two thousand years by the Hindus, reached essentially its present form in the sixth century, and was introduced into the West by Arabic mathematicians in the seventh century. As a result, it is generally called the “Arabic system.” It is almost certainly the most successful conceptual invention of all time and is the only genuinely universal language on earth. It has gained worldwide acceptance because it is far better designed and much more efficient for human usage than any other system.
One of the strengths of the Arabic system is that the number “words” can be read aloud, and moreover, the spoken version reflects the numeric structure in terms of units, multiples of ten, multiples of a hundred, and so forth. (Later we shall consider the arithmetical consequences of the variations in reading Arabic numbers in different languages.)
Another strength of the Arabic system is that it is a language. Consequently, it allows humans—who have an innate linguistic fluency—to use their language ability to handle numbers. Thus, while our intuitive number sense resides in the left parietal lobe, the linguistic representation of exact numbers is handled by the frontal lobe, the language center. I shall have more to say on this later.
Although the use of the symbols 1, 2, 3, 4, 5, 6, 7, 8, 9 for the digits is now universal, in the past there have been others, including Cuneiform, Etruscan, Mayan, ancient Chinese, ancient Indian, and Roman. The Chinese still use a modern variant of their ancient system in addition to Arabic notation, and of course Western societies still use Roman numerals for some specialized purposes.
In the light of our earlier discussions about the special nature of the first three counting numbers, it is of interest to note that in every number representation system ever used, the first three numbers are denoted the same way: 1 is denoted by a single stroke or dot, 2 by placing two such symbols side by side, and 3 by placing three such symbols side by side. In the Roman system, for example, the first three numerals are I, II, III. Mayan notation uses dots: •, ••, •••. The different systems differ only from the fourth numeral onward.
What’s that you say? Our Arabic system does not follow that pattern? Yes, it does. The ancient Indian system used horizontal bars, like this:

When people started to write these symbols without taking the pen from the paper, it yielded this pattern:
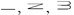
. At some stage the first stroke became vertical. When printing was invented, the numerals were given the stylized versions we use today: 1, 2, 3.
Once you have a system for representing any positive whole number, it can be easily extended to fractional and negative quantities. The introduction of the decimal point or the fraction bar allows us to represent any fractional quantity (3.1415 or
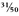
, for example). The minus sign (-) extends the range to all negative quantities, whole or fractional. (Negative numbers were first used by sixth-century Indian mathematicians, who denoted a negative quantity by drawing a circle around the number, but negative numbers were not fully accepted by European mathematicians until the early eighteenth century.)
Incidentally, the original idea of denoting numbers by having a small collection of basic symbols and stringing them together to form number “words” is due to the Babylonians, around 2000 BC. Because it was built on the base 60, the Babylonian system itself was cumbersome to use, and thus did not gain widespread acceptance, although we still use it in geography and our measurement of time (60 minutes make one hour, 60 seconds make one minute).
One of the most powerful aspects of Arabic notation is that arithmetic can be performed through fairly straightforward (and easily learned) manipulations of the symbols. When performing addition, for example, we write all the numbers one beneath the other, aligned in columns starting from the right, and then proceed to add the digits in each column from right to left. Whenever a sum in a column reaches 10, we put a 0 in that column and carry a 1 to the next column to the left. This procedure works for any set of numbers and can be carried out automatically by a machine. For the other basic arithmetical operations, subtraction, multiplication, and division, there is likewise a standard procedure that always works, regardless of what the actual numbers are.
Arabic notation makes basic arithmetic so mindless that in the days before cheap hand-held calculators, elementary arithmetic was one of the least popular classes in schools. It is a great pity that for so many years our teaching methods have obscured one of humankind’s greatest conceptual inventions. The true marvel of the invention of the Arabic number system is lost in the trivia of symbolic manipulation. Arithmetic is a dull and mindless task which our creative intellect has found ways to automate. But let’s not forget what an incredible human invention is the Arabic number system. It is concise and easily learned. It allows us to represent numbers of unlimited magnitude and apply them to collections and measurements of all kinds. Moreover, its greatest strength is precisely that it reduces computation with numbers to the routine manipulation of symbols on a page.
NUMBERS IN THE MIND
Now, despite the fact that everyone is taught to carry out calculations using Arabic notation, you might think that, apart perhaps from the “math types,” most of us attach little significance to what number symbols mean. The more so in view of our observation that our innate number sense does not extend far beyond 3, if at all (except in the sense of making general estimates of collection sizes). But this is not at all the case. Psychologists have known for twenty years that every one of us attaches great significance to each and every counting number we encounter. You may think you are not a “numbers person.” But the evidence says otherwise.
For one thing, consider the number comparison test we encountered earlier, in which you were asked to decide which of two numbers is larger (page 17). This test was first carried out by the American psychologists Robert Moyer and Thomas Landauer in 1967. They flashed pairs of digits, such as 7 and 9, onto a computer screen and asked the subject to declare which was the larger by pressing one of two response keys. The responses were timed electronically.
This sounds easy until you try it. Response times of half a second or more are not uncommon. Moreover, under the pressure of the experiment, subjects sometimes make errors. The surprising result that Moyer and Landauer observed was that, for each individual, the response times varied systematically with the relationship between the numbers presented. Given two numbers with one much smaller than the other, say 3 and 9, subjects responded quickly and accurately. If the two numbers were closer, say 5 and 6, response times were 100 milliseconds or more longer, and subjects gave the wrong answer in as many as one out of ten cases. Moreover, for a fixed separation, response times increased as the numbers got larger. Choosing the larger of 1 and 2 was easy, it took a little longer for 2 and 3, and much longer for 8 and 9.
Variations of the Moyer and Landauer experiment have been repeated many times, always with similar results. What’s going on? The shapes of the actual symbols cannot account for the difference—the pair of symbols 3 and 8 don’t look that much different from 8 and 9, and yet subjects take longer to decide that 9 is greater than 8 than to decide 8 is greater than 3. The critical factor seems to be the number itself, not the symbol.
Further evidence comes when we extend the experiment to two-digit numbers. Try this one. Which is larger, 72 or 69? Got it? All right, here’s another. Which is larger, 79 or 63? If you are like most people who have taken this test, two observations will apply. First, it took you longer to decide that 69 is smaller than 72 than to decide that 63 is smaller than 79. The greater distance between the numbers made the second pair easier. Second, you did not answer the questions in the most efficient way, which is to notice that you need not look past the first digit in each pair. Any two-digit number starting with 6 will be smaller than any two-digit number starting with 7. If you were to answer the question that way, your time should be the same for both examples. But what everybody does is go straight from the symbols to their mental conception of the actual numbers as entire units. This also explains why it takes you only slightly longer to decide which of 67 and 69 is larger than it does for 67 and 71; the fact that the first pair both start with the same digit, whereas the second pair start with different digits, makes hardly any difference. If you based your decision on the symbols rather than the numbers they represented, it would make more of a difference.
Even more dramatic evidence of the way numbers develop a life of their own in our brains was provided in the early 1980s by two Israeli researchers, Avishai Henik and Joseph Tzelgov. They showed subjects pairs of digits in different-sized fonts on a computer screen, and measured the time it took the subject to decide which symbol was printed in the larger font. On the face of it, this task has nothing to do with what number the digit denoted, but only with the size of the actual symbol. Nevertheless, subjects took longer to respond when the relative size of the fonts conflicted with the relative sizes of the numbers. For example, it took longer to decide that the symbol 3 is larger than the symbol 8 than to decide that the symbol 8 is larger than the symbol 3. Subjects were unable to forget that the number 8 is larger than the number 3. This means that digits are not just symbols to which meaning can be attached; they are symbols to which meaning is attached, and closely.
The meanings attached to digits and to multi-digit expressions are numbers, of course, but what does that mean? In what sense do we have numbers in our minds?
Number comparison experiments and other investigations suggest that we have a sort of “mental number line,” where we “see” the numbers as points on a line, with 1 at the left, 2 to its right, then 3, etc. To decide which of two numbers is the larger, we mentally locate them on our mental number line and see which is on the right.
This idea of a mental number line suggests the mathematicians’ number line we learn about in elementary school. But there is one significant difference. On our mental number line, the numbers are not spaced evenly apart as they are on the mathematicians’ number line. Rather, the farther we go along our mental number line, the closer together the numbers appear to be. This explains the results of Moyer and Landauer’s number comparison test. This increasing compression of the numbers makes it more difficult to distinguish the two members of a pair of larger numbers than a pair of smaller numbers. Subjects can decide which is the larger of 5 and 4 much faster than for the pair 53 and 52. Even though the numerical difference between each pair is the same, namely 1, the larger pair seem “closer together” on our mental number line than do the smaller pair.
Moreover, the symbols we use to denote numbers appear to become “hard-wired” into our intuitive number module in the left parietal lobe, in a way that the ordinary language number words (handled by the frontal lobe) do not. In The Mathematical Brain, Butterworth gives some clinical evidence to support this apparent distinction.
For instance, Butterworth reports, there are people who are unable to read words but who can read aloud single or multi-digit numbers presented to them using numerals. Conversely, there is a man—Dottore Foppa, an early Alzheimer’s sufferer—who can read words, including number words and word expressions for multi-digit numbers, but is unable to read aloud a number of two or more digits presented to him in numerals. An extreme case is presented by Donna, a woman who had surgery to her left frontal lobe. Although she can read and write single- or multi-digit numbers in numerals, not only can she neither read nor write words, she can name only about half the letters of the alphabet. Despite being unable to write her own name—the result is an illegible scribble—on a standard arithmetic test (where the questions are presented in purely numeric form) she does just fine, writing her numerals neatly, in columns, and invariably getting the right answer.
In other words, a number system such as the Arabic system may indeed be a language, but it is a very special one handled in a different region of the brain from normal language. If (as I suggested earlier) our counting ability derived from finger use by our ancestors—a physical process controlled by the same left parietal lobe in which resides our number sense—this distinction between number symbols and number words is just what one would expect if our number symbols derive from the use of our fingers and number words come from ordinary language.
Incidentally, some individuals who are unable to compare pairs of numbers “by inspection” using their number sense can nevertheless tell which of two numbers is the larger by counting—they start to count 1, 2, 3, etc., and see which number they reach first. Since memorization of the number sequence is a linguistic feat, this strategy would appear to make use of the brain’s language faculty to make up for a lack of number sense.
Similarly, some people who cannot add or subtract pairs of fairly small numbers from memory use a counting-on strategy. To add 5 and 4 they will proceed thus: “Five, six, seven, eight, nine—the answer is nine.” They may recite the numbers out loud, or in their heads, and may use their fingers to keep track of how many words they say. This approach is more efficient if the larger of the given pair of numbers is taken as the starting point for the count, so individuals who can compare pairs of numbers have an advantage over people who cannot. To calculate 6—3 they will recite (internally or out loud, and often counting the words on their fingers): “three, four, five, six—the answer is three.”
The idea of a mental number line also explains the following phenomenon. (To get the proper effect, it is important that you follow my instructions exactly, in the order I give them. Don’t look ahead to see what’s coming next.)
Memorize the following list of digits: 7, 9, 6, 8.
Cover up the list with your hand.
Now count down from 16 to 1 in threes. Keep the list covered up.
Have you done that?
Keep the list covered up until you have finished counting.
Now tell me whether 5 was in the list you just remembered. Was 1 in the list?
Now you can uncover the list.
Almost certainly, you felt pretty confident that 1 was not in the list, but less certain about 5. The explanation is that you formed a mental image of the list as consisting of numbers in the region of 6 and 7 on your mental number line. When later asked if 5 was in the list, you were not sure, because 5 is in the general region of the list. But because 1 is well away from that region, you were confident it was not in the list.
Only about 14 percent of adults say they are conscious of having a mental number line. Of these, most of those whose primary language reads left to right claim that their number line runs left to right, although some say theirs goes upward, and a few see it running downward. However, in an ingenious experiment performed in 1993, Dehaene and his colleagues showed that most of us have a mental number line, even if we are not aware of it, and that we compare pairs of numbers by comparing their positions on our mental number line.
Dehaene presented subjects with a series of numbers on a computer screen, which they had to categorize as even or odd, as rapidly as possible, by pressing one of two buttons. For half the subjects, the “odd” button was in their left hand, the “even” button in their right; for the other half, they were reversed. The computer timed the subjects’ responses. The outcome was amazing. With small numbers, subjects responded faster with their left hand; with larger numbers, they were faster with their right hand. Dehaene’s explanation for this difference is that the subjects “saw” the numbers arranged spatially on a left-to-right line. Smaller numbers were at the left of this line, so the subjects responded faster with their left hand; larger numbers were on the right, and this led to a faster response with the right hand.
Interestingly, there were some Iranian students in the group tested, and their responses were reversed—they were faster with their right hands for smaller numbers and faster with their left hands for larger numbers. Iranians read right to left, of course. Thus it appears that our mental number line generally runs in the direction of our reading.
THE SOUND OF NUMBER
A few years ago I attended a luncheon at which the mathematician Arthur Benjamin was giving a demonstration of his amazing feats of mental arithmetic. Just before he was due to begin, he asked to have the air conditioning turned off. While we were waiting for the organizers to find someone who had access to the control room, Benjamin explained that the hum from the air conditioning system would interfere with his calculations. “I recite the numbers in my head to store them during the calculation,” he said. “I have to be able to hear them, otherwise I forget them. Certain noises get in the way.” In other words, one of Benjamin’s secrets as a human calculator was his highly efficient use of linguistic patterns—the sounds of the numbers as they echoed in his mind.
Although few of us can match Benjamin’s ability to calculate square roots of six-digit numbers, we all use the human ability to remember a spoken linguistic pattern when we learn our multiplication table. We learn by reciting the table over and over. Even today, forty-five years after I “learned my tables,” I still recall the product of any two single-digit numbers by reciting that part of the table in my head. I remember the sound of the number words spoken, not the numbers themselves. Indeed, I believe the pattern I hear in my head is precisely the one I learned when I was seven years old!
Despite many hours of practice, most people encounter great difficulty with the multiplication tables. Ordinary adults of average intelligence make mistakes roughly 10 percent of the time. Some multiplications, such as 8 × 7 or 9 × 7, can take up to two seconds, and the error rate goes up to 25 percent. (The answers are 8 × 7 = 54 and 9 × 7 = 64. Or are they? Oh dear! I’ll leave it to you to sort out.)
Why do we have such difficulty? Discounting the one times table and the ten times table as presenting no difficulty, the entire collection of multiplication tables amounts to only sixty-four separate facts (each one of 2, 3, 4, . .., 9 multiplied by each one of 2, 3, 4, ..., 9). Most people have little problem with the two times table or the five times table. Discounting their entries leaves just thirty-six single-digit multiplications where it takes some effort to commit them to memory. (Each of 3, 4, 6, 7, 8, 9 times each of 3, 4, 6, 7, 8, 9.) In fact, anyone who remembers that you can swap the order in multiplication (for example, 4 × 7 is the same as 7 × 4) can cut the total in half, to eighteen. So, the total number of individual facts that have to be learned to master all the multiplication tables is eighteen. That’s all, eighteen!
To put that figure of eighteen simple facts in perspective, consider that by the age of six, a typical American child will have learned to use and recognize between 13,000 and 15,000 words. An American adult has a comprehension vocabulary of around 100,000 words and makes active and fluent use of 10,000 to 15,000. Then there are all the other things we remember: people’s names, phone numbers, addresses, book titles, movie titles, etc. Moreover, we learn these facts with hardly any difficulty. We certainly don’t have to recite words and their meanings over and over the way we do our multiplication tables. In short, most of the time there is nothing wrong with our memories. Except when it comes to the eighteen key facts of multiplication. Why?
Self-appointed critics of American youth seem to gain satisfaction from blaming the laziness of students. It seems clear to me, however, that there must be something about the multiplication tables that makes them all but unlearnable. Such a widespread problem with multiplication surely indicates some feature of the human brain that requires investigation, not criticism. There is something significant for us to learn here, and it’s not our multiplication tables.
The human mind is a pattern recognizer. Human memory works by association—one thought leads to another. Someone mentions Grandfather, and that brings to mind the time he took us to the ball game, where we saw a woman who looked just like Aunt Alice, who went to live in Australia, which is where you find kangaroos, which reminds me of that kangaroo we saw in Bristol Zoo, and on and on it can go. The ability to see patterns and similarities is one of the greatest strengths of the human mind.
The human mind works very differently from a digital computer. Furthermore, each is highly unsuited to perform certain tasks that the other does with ease. Computers are good at precise storage and retrieval of information and exact calculation. A modern computer can perform billions of multiplications in a single second, getting each one right. But, despite an enormous investment in money, talent, and time over fifty years, attempts to develop computers that can recognize faces or indeed make much sense at all of a visual scene have largely failed. Humans, on the other hand, recognize faces and scenes with ease, because human memory works by pattern association. For the same reason, however, we can’t do some things that computers do with ease, including remembering multiplication tables.
The reason we have such trouble is that we remember the tables linguistically, and as a result many of the different entries interfere with one another. A computer is so dumb that it sees 7 × 8 = 56, 6 × 9 = 54, and 8 x 8 = 64 as quite separate and distinct from each other. But the human mind sees similarities between these three multiplications, particularly linguistic similarities in the rhythm the words make when we recite them out loud. Our difficulty in trying to keep these three equations separate does not indicate a weakness of our memory but one of its major strengths—its ability to see similarities. When we see the pattern 7 × 8, it activates several patterns, among which are likely to be 48, 56, 54, 45, and 64.
Dehaene makes this point brilliantly in
The Number Sense with the following example: suppose you had to remember the following three names and addresses:
• Charlie David lives on Albert Bruno Avenue.
• Charlie George lives on Bruno Albert Avenue.
• George Ernie lives on Charlie Ernie Avenue.
Remembering just these three facts looks like quite a challenge. There are too many similarities, and as a result each entry interferes with the others. But these are just entries from the multiplication tables. Let the names Albert, Bruno, Charlie, David, Ernie, Fred, and George stand for the digits 1, 2, 3, 4, 5, 6, and 7, respectively, and replace the phrase “lives on” by the equals sign, and you get the three multiplications:
• 3 × 4 = 12
• 3 × 7 = 21
• 7 × 5 = 35
It’s the pattern interference that causes our problems.
Pattern interference is also the reason why it takes longer to realize that 2 × 3 = 5 is false than to realize that 2 × 3 = 7 is wrong. The former equation is correct for addition (2 + 3 = 5), and so the pattern “2 and 3 makes 5” is familiar to us. There is no familiar pattern of the form ”2 and 3 makes 7.”
We see this kind of pattern interference in the learning process of young children. By the age of seven, most children know by heart many additions of two digits. But as they start to learn their multiplication tables, the time it takes them to answer a single-digit addition sum increases, and they start to make errors such as 2 + 3 = 6.
Linguistic pattern similarities also interfere with retrieval from the multiplication table when we are asked for 5 × 6 and answer 36 or 56. Somehow, reading the 5 and the 6 brings to mind both incorrect answers. People do not make errors such as 2 × 3 = 23 or 3 × 7 = 37. Because the numbers 23 and 37 do not appear in any multiplication table, our associative memory does not bring them up in the context of multiplication. But 36 and 56 are both in the table, so when our brain sees 5 × 6, both are activated.
In other words, much of our difficulty with multiplication comes from two of the most powerful and useful features of the human mind: pattern recognition and associative memory.
To put it another way, millions of years of evolution have equipped us with a brain that has particular survival skills. Part of that endowment is that our minds are very good at recognizing patterns, seeing connections, and making rapid judgments and inferences. All of these modes of thinking are essentially “fuzzy.” Although the term “fuzzy thinking” is often used pejoratively, to mean sloppy and inadequate thinking, that is not my intended meaning here. Rather, I am referring to our ability to make sensible decisions rapidly from relatively little information. This is a powerful ability well beyond our biggest and fastest computers. Our brains are not at all suited to the kinds of precise manipulations of information that arise in arithmetic—they did not evolve to do arithmetic. To do arithmetic, we have to marshal mental circuits that developed (i.e., were selected for during our evolution) for quite different reasons. It’s like using a small coin to drive in a screw. Sure, you can do it, but it’s slow and the outcome is not always perfect.
We learn the multiplication tables by using our ability to remember patterns of sound. So great is the effort required to learn the tables (because of the interference effects) that people who learn a second language generally continue to do arithmetic in their first language. No matter how fluent they become in their second language—and many people reach the stage of thinking entirely in whichever language they are conversing in—it’s easier to slip back into their first language to calculate and then translate the result back, than to try to relearn the multiplication table in their second language. This formed the basis of an ingenious experiment Dehaene and his colleagues performed in 1999 to confirm that we use our language faculty to do arithmetic.
The hypothesis they set out to establish was this: that arithmetical tasks that require an exact answer depend on our linguistic faculty—in particular, they use the verbal representations of numbers—whereas tasks that involve estimation or require an approximate answer do not make use of the language faculty.
To test this hypothesis, the researchers assembled a group of English-Russian bilinguals and taught them some new two-digit addition facts in one of the two languages. The subjects were then tested in one of the two languages. For questions that required an exact answer, when both the instruction and the question were in the same language, subjects answered in 2.5 to 4.5 seconds, but took a full second longer when the languages were different. The experimenters conclude that the subjects used the extra second to translate the question into the language in which the facts had been learned.
When the question asked for an approximate answer, however, the language of questioning did not affect the response time.
The researchers also monitored the subjects’ brain activity throughout the testing process. When the subjects were answering questions that asked for approximate answers, the greatest brain activity was in the two parietal lobes—the regions that house the number sense and support spatial reasoning. Questions requiring an exact answer, however, elicited far more activity in the frontal lobe, where speech is controlled.
Altogether, the result was pretty convincing. The ability of humans to extend the intuitive number sense (which is not unique to humans) to a capacity to perform exact arithmetic (which does appear to be uniquely human) seems to depend on our language faculty. But if that is true, wouldn’t we expect to see differences in arithmetical ability from one country to another? If the words used for numbers are significantly different, shouldn’t this affect how well people learn their tables?
This is indeed what happens.
THE CHINESE ADVANTAGE
Every few years, the newspapers report that American schoolchildren have scored poorly in yet another international comparison of mathematical ability. Although there is never any shortage of knee-jerk reactions to such news, it is in fact extremely difficult to draw reliable conclusions from cross-national and cross-cultural comparisons. Many factors are involved, and even if there is a real problem, simplistic solutions are unlikely to have much effect. Education and learning are not simple matters, nor is the relationship between the two.
Chinese and Japanese children consistently outperform American children on these tests. They also outperform children from much of Western Europe, who tend to do about as well as the Americans. Given the cultural similarities between the United States and Western Europe, and the difference between those cultures and the ones of China and Japan, it is reasonable to suppose that cultural differences contribute to the disparity. Differences among the school systems are surely involved as well. But so too is language. Doing arithmetic, and in particular learning multiplication tables, is simply easier for Chinese and Japanese children, because their number words are much shorter and simpler—generally a single, short syllable such as the Chinese si for 4 and qi for 7.
The grammatical rules for building up number words in Chinese and Japanese are also much easier than in English or other European languages. For instance, the Chinese rule for making words for numbers past ten is simple: 11 is ten one, 12 is ten two, 13 is ten three, and so on, up to two ten for 20, two ten one for 21, two ten two for 22, etc. Think how much more complicated is the English system. (It’s even worse in French and German, with their quatre-vingt-dix-sept for 97 and vierundfünfzig for 54.) A recent study by Kevin Miller showed that language differences cause Englishspeaking children to lag a whole year behind their Chinese counterparts in learning to count. By the age of four, Chinese children can generally count up to 40. American children of the same age can barely get to 15, and it takes them another year to get to 40. How do we know the difference is due to language? Simple. The children in the two countries show no age difference in their ability to count from 1 to 12. Differences appear only when the American children start to encounter the various special rules for forming number words. The Chinese children, meanwhile, simply keep applying the same ones that worked for 1 to 12. (American children often apply the same rules, but they find they have made a mistake when they try to use words like twenty-ten and twenty-eleven.)
In addition to being easier to learn, the Chinese number word system also makes elementary arithmetic easier, because the language rules closely follow the base-10 structure of the Arabic system. A Chinese pupil can see from the linguistic structure that the number “two ten five” (i.e., 25) consists of two 10s and one 5. An American pupil has to remember that “twenty” represents two 10s, and hence that “twenty-five” represents two 10s and one 5.
It is remarkable how often we dragoon our linguistic ability into helping us learn important number facts (such as multiplication tables) and do arithmetic. But as often happens when we take a tool developed for one purpose and use it for another, the outcome can be less than ideal.
WHY MATHEMATICS SEEMS ILLOGICAL
To be able to use numbers properly, it is not enough to know how to manipulate the symbols according to the rules. You also have to relate the symbols and your manipulations of them to your innate sense of number —to the numerical quantities the symbols denote. Otherwise, because our minds automatically see patterns, we can easily find ourselves performing nonsensical manipulations of symbols.
For example, the following incorrect sum illustrates a common error in adding fractions:
A person who makes this mistake sees this as two addition sums, first adding the numerators 1 + 3 = 4 and then adding the denominators 2 + 5 = 7. Symbolically, this is the most logical thing to do. It is incorrect because it makes no sense in terms of the numbers the symbols represent. The symbolic manipulations you have to perform to get the correct answer—the ones that correspond to adding the actual fractional numbers represented by the symbol words ½ and ⅗—are fairly complicated. What is more, those symbol-manipulation rules only make sense if you think of the numbers the symbols represent. Purely as rules for manipulating symbols, they make no sense at all.
It is undoubtedly because of such cases that many children come to see mathematics as “illogical” and “full of rules that make no sense.” They think of mathematics as a collection of rules for doing things with symbols. Some of these rules make sense; others seem quite arbitrary. The only way to avoid this misconception is for teachers to ensure that their pupils understand what the symbols represent. This is rarely done. How then do some children learn how to add fractions correctly?
Since the human mind is an excellent pattern recognizer with tremendous adaptive powers, with enough training it can learn to perform almost any symbolic procedure in an essentially “mindless” fashion. Thus, it is possible to memorize a procedure for manipulating the symbols to add fractions correctly:
Start out by multiplying the two denominators. That will give you the denominator in the answer. Then multiply the numerator of the first fraction by the denominator of the second, and the numerator of the second fraction by the denominator of the first, and add those two results. That gives you the numerator in the answer. Then see if there are any numbers that divide both the numerator and the denominator in your answer, and if there are, divide both numerator and denominator by that number. Repeat this double division until you can’t find any such common divisors. What’s left is your final answer.
This procedure looks complicated—and at a symbolic (i.e., linguistic) level it makes no sense at all. But with practice most people can learn to follow it. Evolution has equipped us with a brain that is actually pretty good at learning particular sequences of actions. But unless someone, at each step, shows you what is going on in terms of the numbers represented by the symbols, the whole thing is just so much mumbo-jumbo. Learn how to perform the mumbo-jumbo and you get an A. How many children leave school with good grades in mathematics but no understanding of what they were doing? Surely a lot, judging from the large numbers of perfectly intelligent adults who cannot add fractions. If only they understood what was going on, they would never forget how to do it. Without such understanding, however, few can remember such a complicated procedure for long once the final exam has ended.
And without understanding, there is little mystery why, for many people, elementary school arithmetic is well summed up by Lewis Carroll’s satirical terms ambition, distraction, uglification, and derision.
Here are some other difficulties that arise from blindly applying a symbolic rule without linking the symbols to the numbers they represent. Answer the following questions:
• A farmer has 12 cows. All but 5 die. How many cows remain?
• Tony has 5 balls, which is 3 fewer than Sally. How many balls does Sally have?
Readers of this book might well score above average on these. But I know from experience that many intelligent people get one or both of them wrong. The numbers 12 and 5 in the first problem, together with the question “How many remain?” create a strong temptation to perform the subtraction 12—5 = and give 7 as the answer. The correct answer is 5, but to get it you have to think what the problem is actually saying. Blindly rushing to the symbolic manipulation stage sometimes works, but not here. Overall it is a disastrous strategy to follow. The symbols are there to assist our reasoning, not eliminate it.
Similarly for the second problem. You see the numbers 5 and 3 together with the word “fewer” and the temptation is to perform the subtraction 5—3 = 2. Again, a hasty leap to symbolic manipulation has led to the wrong answer. When you stop and think what the question is saying, you realize you should add 3 to 5, giving the correct answer that Sally has 5 + 3 = 8 balls.
People who are “good at arithmetic” do not make such mistakes. What sets them apart from the many people who never seem to “get it” is not that they have memorized the rules better. Rather, they understand those rules. Indeed, their understanding is such that they don’t really have need for the rules at all. This is true for the many people for whom numbers bring no fear, but the most dramatic illustration is provided by the lightning calculators, such as Arthur Benjamin, whom we met briefly earlier, who are able to perform highly complicated calculations rapidly in their heads.
Part of the calculating wizards’ secret is that, for them, many numbers have meaning. For most of us who are comfortable with numbers, a number such as 587 doesn’t mean anything—it’s just a number. But to a calculating wizard, that number word 587 may well have meaning—it may conjure up a mental image—just as the English word “cat” has meaning for us and conjures up an image in our minds.
Some numbers, of course, do have meaning for us. Americans see meaning in the numbers 1492 (Columbus’s discovery of America) and 1776 (the signing of the Declaration of Independence); Britons see meaning in 1066 (the Battle of Hastings); and anyone with a technical education sees meaning in the number 314159 (the start of the decimal representation of the mathematical constant π). Other numbers that have meaning for us—and which we therefore remember—are our birthdate and our telephone number.
For a calculating wizard, however, many numbers have meaning. Generally, that meaning lies not in the everyday world of dates, ID cards, and telephone numbers, but in the world of mathematics itself. For instance, Wim Klein, a famous calculating wizard who in the days before electronic computers once held a professional position with the title “computer,” observes, “Numbers are friends to me.” Referring to the number 3844, he says, “For you it’s just a three and an eight and a four and a four. But I say, ‘Hi, 62 squared!’”
Because numbers have meaning to Klein and the other calculating wizards, calculation is meaningful to them. Consequently, for reasons I shall elaborate in due course, they are much better at it.
Of course, lightning calculators are a very special case. Most of us would not want to develop such a skill even if we could. But the point is that arithmetic becomes much easier when you understand what it is about —when the symbols mean something to you. Not seeing the meaning is the main reason so many people say that they are “no good at math.”
I end this chapter with two notes of caution.
First caution: I have tried to show how our facility for language—particularly our ability to recognize and remember linguistic patterns—helps us do mathematics, particularly basic arithmetic. I am not saying that we do mathematics using ordinary language. Rather, the examples I have given show how we sometimes use linguistic skills as a tool to assist us.
In fact, based on subjective reports by mathematicians, myself included, it is almost certainly the case that we do not use language to actually do mathematics. We do use language to record and convey the results of our thinking—indeed, on occasion to convey our actual thought processes. But the thinking process itself, what we generally call “doing mathematics,” is not linguistic.
Second caution: I announced at the very beginning of this book that my goal is to convince you that the ability to do mathematics is based on our facility for language. The discussions in this chapter have virtually nothing to do with that overall claim. It will in fact take me some considerable time to make my case—that’s why this is a book and not a short pamphlet. For now, let me reiterate that the principal claim in this book is not that we use language to do mathematics, but that the feature of our brain that enables us to use language is the same feature that makes it possible for us to do mathematics. Thus when the human brain developed the ability to use language, it automatically acquired the ability to do mathematics. When I come to spell out my case in detail, it will be at a fairly deep level, involving the nature of mathematics and the nature of language. It’s time to take a look at the first of these: the nature of mathematics. Not number, mathematics.
 When people started to write these symbols without taking the pen from the paper, it yielded this pattern:
When people started to write these symbols without taking the pen from the paper, it yielded this pattern: 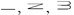 . At some stage the first stroke became vertical. When printing was invented, the numerals were given the stylized versions we use today: 1, 2, 3.
. At some stage the first stroke became vertical. When printing was invented, the numerals were given the stylized versions we use today: 1, 2, 3.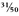 , for example). The minus sign (-) extends the range to all negative quantities, whole or fractional. (Negative numbers were first used by sixth-century Indian mathematicians, who denoted a negative quantity by drawing a circle around the number, but negative numbers were not fully accepted by European mathematicians until the early eighteenth century.)
, for example). The minus sign (-) extends the range to all negative quantities, whole or fractional. (Negative numbers were first used by sixth-century Indian mathematicians, who denoted a negative quantity by drawing a circle around the number, but negative numbers were not fully accepted by European mathematicians until the early eighteenth century.)