
Was hier im Titel unter »abgründige Beziehungen« und »unfundierte Operationen« firmiert, ist ein Markenzeichen der spekulativen Philosophie. Da ich mit meiner Vorliebe für die Spekulation bei meinen Freunden aus der analytischen Philosophie regelmäßig anecke, habe ich mir angewöhnt, auf einem Umweg für sie zu werben. Liebe Freunde, pflege ich zu sagen, ihr kennt doch zweifellos die mathematische Logik und die Mengenlehre, und dies natürlich viel besser als ich, der Laie vom kontinentalen Ufer. So wisst ihr auch, was es mit dem Extensionalitätsaxiom und mit dem Fundierungsaxiom auf sich hat. Ersteres besagt: »Umfangsgleiche Mengen sind gleich«, und bindet damit die Identität einer Menge an die Identität ihrer Elemente. Letzteres besagt: »Alle Mengen sind fundiert«, was darauf hinausläuft, dass keine Menge eine unendliche absteigende Elementschaftskette hat. Eine unendliche absteigende Elementschaftskette käme nach dem Extensionalitätsaxiom einem unendlichen Regress in der Individuation der betreffenden Menge gleich. Wer sich vor Abgründen fürchtet, sollte also besser das Fundierungsaxiom unterschreiben.
Nun gibt es aber furchtlose Mengentheoretiker wie Peter Aczel, der gezeigt hat, dass die Mengenlehre nicht widerspruchsvoll wird, wenn man das Fundierungsaxiom durch ein Antifundierungsaxiom, AFA, ersetzt, dem zufolge es auch unfundierte Mengen gibt, darunter an prominenter Stelle diejenige Einermenge, deren einziges Element diejenige Einermenge ist, deren einziges Element diejenige Einermenge ist, deren einziges Element usf. ad infinitum. Aczel nennt diese Einermenge, die allein durch den Abgrund in ihrer Individuation definiert ist, Ω und zeigt, dass der Abgrund einem Zirkel gleichkommt: Ω ist die Einermenge ihrer selbst. Unendliche Regresse in der Individuation einer Menge lassen sich stets auch als Zirkel darstellen. Regress und Zirkel sind äquivalent und nur darstellungstechnisch unterschieden. Für Ω gilt:

Ω ist die total unfundierte Einermenge und ipso facto die Einer-mengeihrerselbst. Als Menge ist sie ein abstraktes Objekt, bezüglich dessen man sich fragen kann, ob es existiert oder nicht. Wenn aus seiner Existenz ein Widerspruch folgen würde, würde man natürlich seine Existenz verneinen. Da kein Widerspruch folgt, ist die Existenzfrage offen.
Ob es die Einermenge Ω gibt, darf uns gleichgültig sein; sie hat ihre Freunde und ihre Gegner unter den Mengentheoretikern. Aber wir sind nicht an mengentheoretischer, sondern philosophischer Theoriebildung interessiert. Nur dies halten wir fest. Wenn unsere Freunde aus der analytischen Philosophie jetzt zu lamentieren begännen, sie verstünden nicht, was mit den Worten »die Einermenge ihrer selbst« gemeint ist, so hätten nicht wir ein Problem, sondern sie. Diese Begriffsbildung lassen wir uns von ihnen nicht schlechtreden.
Das Wort »Einermenge« bezeichnet das Resultat einer Operation, der Operation der Einermengenbildung. Eine solche Operation ist ein abstrakter Eingabe/Ausgabe-Apparat. Wird etwas eingegeben, so liefert der Apparat eine Ausgabe. Und vielleicht funktioniert der Apparat sogar im Leerlauf und liefert dann selbst seine ursprüngliche Eingabe. So würde es sich zumindest im Fall der Einermenge ihrer selbst verhalten. Ein konkreter, substantieller Automat aus Plastik, Holz oder Metall, etwa eine Kaffeemühle, könnte so natürlich nicht funktionieren. Das wäre eine rechte Wundermühle, vergleichbar dem Tischlein deck dich, die das einzugebende Mahlgut immer schon vorher selbst ermahlen hätte, so dass man nie Kaffeebohnen zu kaufen brauchte. Aber bei einem rein mathematischen oder rein begrifflichen Apparat müssen wir uns das Wunder als eine ernstzunehmende Theorieoption gefallen lassen, wie Peter Aczels total unfundierte Einermenge zeigt.
Manche Theoretiker quer durch die Philosophiegeschichte haben sich tatsächlich dergleichen Begriffsbildungen gefallen lassen, zum Beispiel in Gestalt kausaler Schleifen, bekannt unter der Überschrift »causa sui«, oder in der Gestalt unendlicher Ursachenregresse. Immerhin dürfen wir nun unter Verweis auf die Einermenge ihrer selbst die Äquivalenz von kausalen Abgründen und kausalen Schleifen konstatieren: Wer unendliche Ursachenregresse zulässt, kann ebenso gut eine causa sui zulassen. Wenn ein Freund unendlicher Kausalregresse die Nachbarschaft der causa-sui-Leute scheut und protestiert: »Aber Ursachen sind zeitlich früher als ihre Wirkungen; deswegen kann sich der Ursachenregress nicht zum Zirkel schließen«, so werden wir ihm antworten: »Dann gib Obacht, dass du dich mit deinen unendlichen Kausalregressen nicht am Ende auf eine zirkuläre Zeit festlegst!«
Wir lassen uns jedenfalls von diesem Protest nicht beeindrucken, denn was der Einermengenbildung recht ist, muss anderen Operationen billig sein. Sofern unsere analytischen Freunde das Wort »Ursache« verstehen, sollten sie auch verstehen, was mit einer Ursache ihrer selbst gemeint ist. Sobald sie das Wort »Wissen« verstehen, sollten sie verstehen, was mit dem Wissen seiner selbst gemeint ist. Sobald sie verstehen, was Wahrheitsfunktionen oder Wahrheitsoperationen sind, sollten sie verstehen, was mit der Negation ihrer selbst und der Affirmation, Konjunktion, Alternation (usw.) ihrer selbst gemeint ist. In all diesen Fällen liegt wie bei der Mengenbildung jeweils ein Voraussetzungsverhältnis vor. Ein Wissen setzt einen Gehalt voraus, durch den es sich von anderen Wissensfällen unterscheidet. Eine Wirkung setzt eine Ursache als Grund ihres Eintretens voraus. Eine n-stellige Wahrheitsfunktion setzt n Aussagen voraus, damit sie als Wert eine komplexe Aussage liefern kann.
Diese Sachverhalte sollen in der Folge betrachtet werden, zuerst kurz der Fall des Wissens seiner selbst oder des Selbstbewusstseins, der uns zu dem der causa sui führen wird, dann ausführlicher der Fall unfundierter Wahrheitsfunktionen. Am Ende sollten Freunde der analytischen Philosophie überzeugt sein, dass spekulative Philosophie kein Humbug ist, und Freunde der spekulativen Philosophie, dass die analytische Philosophie schnell gelernt ist und sehr hilfreich, um komplexe Sachverhalte präziser zu verstehen.
»Das Selbst«, sagt an vielzitierter Stelle Kierkegaard, »ist ein Verhältnis, das sich zu sich selbst verhält, oder es ist das an dem Verhältnisse, dass das Verhältnis sich zu sich selbst verhält; das Selbst ist nicht das Verhältnis, sondern dass das Verhältnis sich zu sich selbst verhält.«1 Demnach dürfte er das einfache Verhältnis, unter Absehung von seinem Sich-zu-sich-Verhalten, mit dem identifizieren, was Brentano als Intentionalität gefasst hat, und insbesondere mit der perzeptuell erfüllten Intentionalität, also dem Wahrnehmungsbewusstsein. Etwas dem Anschein nach an sich der Fall Seiendes ist zugleich für unser Bewusstsein. Reinhold und Hegel hatten diesen Sachverhalt vor Augen, als sie ihre jeweiligen Varianten des Satzes des Bewusstseins formulierten. Nun verhält sich dieses einfache Verhältnis von Für-uns (oder Für-das-Bewusstsein) und An-sich nach Kierkegaards Formulierung außerdem auch noch zu sich selbst. Bewusstsein als solches ist demnach immer auch schon implizites Selbstbewusstsein. Mit Sartre können wir dieses implizite Selbstbewusstsein das präreflexive und das nachgeordnete ausdrückliche Selbstbewusstsein das reflexive nennen. Die Reflexion macht den impliziten Zirkel explizit, der schon im Bewusstsein als solchem liegt, sofern dieses sich immer schon auch zu sich verhält.
»[C]’est la nature même de la conscience d’exister ›en cercle‹«, sagt Sartre zu Beginn von »L’être et le néant« und fügt einige Zeilen weiter hinzu: »D’un seul coup elle [la conscience] se détermine comme conscience de perception et comme perception.«2 Das Bewusstsein bestimmt sich mit einem Schlag als einfache Wahrnehmung und als Bewusstsein von der Wahrnehmung – als perzeptuelles Verhältnis und als Sich-zu-sich-Verhalten dieses perzeptuellen Verhältnisses, mit Kierkegaard zu reden. Entdeckt hat diesen fundamentalen Zirkel des Bewusstseins wohl Fichte oder, wenn nicht entdeckt, so zum ersten Mal in der Philosophiegeschichte zur Pointe erhoben und ihn terminologisch als Tathandlung gefasst, d. h. als diejenige Handlung, in welcher das Ich (oder das Selbst oder das Selbstbewusstsein) sich selber setzt, sich selber sozusagen erdenkt und erfindet. Hier also zeigt sich eine wesentliche begriffliche Verbindung zwischen dem Gedanken eines zirkulären oder unfundierten Wissens und eines zirkulären oder unfundierten Ursache-Wirkungs-Verhältnisses. Das Ich, das sich selber setzt, ist in seinem Setzen eine Art causa sui und in seinem Gesetztsein ipso facto eine Art effectus sui, allerdings eine recht luftige und nichtige causa sui, die von etwas anderem, Substantiellerem zehrt, darin vergleichbar einem Virus mit zwar eigener DNS, aber ohne eigenen Stoffwechsel, das nur in einem Wirtsorganismus existieren und sich reproduzieren kann. So kann auch das Selbst nur an einem perzeptuellen Verhältnis existieren, in dem ein konkreter leiblicher Organismus zu seiner Umgebung steht, an diesem Organismus und seinem Wahrnehmungsbewusstsein dann aber in einer zirkulären, causa-sui-artigen Struktur.
Nun kann man im Falle unfundierter Mengen sowie unfundierten Wissens und unfundierter Wirkungen ergebnisoffen diskutieren, ob es dergleichen gibt. Für das unfundierte Wissen und zugleich die unfundierte Wirkung spricht das evidente Phänomen des Selbstbewusstseins. Aber andererseits ist auch klar, dass es eine substantielle causa sui von der Art einer Kaffeemühle, die sich selber ermahlt oder einem 3D-Drucker, der sich selber ausdruckt, nicht geben kann. Nach aristotelischer Lehre sind Akzidentien für sich genommen nichts und seiend nur in Beziehung auf eine Substanz, nämlich bloße Modifikationen von deren substantiellem Sein. Ohne näher untersuchen zu wollen, ob das Substanz-Akzidens-Modell hier ganz angemessen ist, wollen wir in ungeschützter, aber illustrativer Rede nur sagen, dass das Selbstbewusstsein ein unfundiertes Wissen und zugleich eine unfundierte Wirkung ist, aber für sich genommen nichts, also keine substantielle, sondern gleichsam nur eine akzidentelle causa sui.
Unsere basalen Wahrheitsansprüche sind Ansprüche auf objektive, meinungsunabhängige Geltung. Aus der stets mitbeanspruchten Meinungsunabhängigkeit folgt für die Erkenntnistheorie unsere Fehlbarkeit und für die Logik und Semantik die Zweiwertigkeit unserer Aussagen: Sie sollen wahr und können falsch sein, sind also wahr oder falsch. Die Zweiwertigkeit wird durch die klassische Logik, konkret das Nichtwiderspruchs- und das Bivalenzprinzip, weiter präzisiert: Jede Aussage soll genau einen von zwei möglichen Wahrheitswerten haben, nicht beide auf einmal, aber auch nicht keinen von beiden. Auf dieser monumentalen und einfachen Basis lässt sich sodann die klassische wahrheitsfunktionale Aussagenlogik aufbauen.
Rein kombinatorisch kann man sich leicht klarmachen, dass es bei zwei Wahrheitswerten vier einstellige und 16 zweistellige Wahrheitsfunktionen gibt (dreistellige kann man bereits vernachlässigen, denn was wir mit dreistelligen Wahrheitsfunktionen ausdrücken können, können wir auch mit zweistelligen ausdrücken). Von den vier einstelligen Wahrheitsfunktionen wird in der Aussagenlogik normalerweise nur die Negation durch ein eigenes Symbol, etwa die Tilde, bezeichnet und von den 16 zweistelligen Wahrheitsfunktionen nur die Konjunktion, die Alternation, das Konditional und das Bikonditional, manchmal noch die Negation der Konjunktion (durch den sogenannten Sheffer-Strich).
Die vier einstelligen Wahrheitsfunktionen, nennen wir sie f, g, h und i, lassen sich bekanntlich durch folgende Wahrheitstafeln charakterisieren:
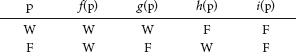
Man erkennt in dieser Tafel die Negation leicht daran, dass sie die Wahrheitswerte umkehrt: aus einer wahren Eingabe eine falsche Ausgabe und aus einer falschen Eingabe eine wahre Ausgabe macht. Es ist die Funktion h. Doch statt »h(p)« schreibt man natürlich »~(p)«.
Die drei übrigen einstelligen Wahrheitsfunktionen sind vergleichsweise uninteressant. Die Funktion f macht aus beliebigen Eingaben wahre und die Funktion i aus beliebigen Eingaben falsche Ausgaben, und g lässt alles, wie es ist. Diese drei Funktionen – die Wahrmacherfunktion, die Falschmacherfunktion und die Identitätsfunktion – werden in der Aussagenlogik vernachlässigt und erhalten jedenfalls keine eigenen Symbole.
Bei den zweistelligen Wahrheitsfunktionen beschränke ich mich auf die üblichen fünf:

Die gebräuchlichen Symbole (für Konjunktion, Alternation, Konditional, Bikonditional und Sheffer-Strich) seien zur Erläuterung hinzugefügt:
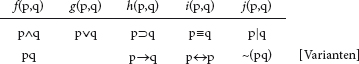
So weit ist alles gang und gäbe und recht trivial. Jetzt aber gehen wir zu einer kleinen Logik unfundierter Aussagen über. Die Frage, ob es unfundierte Mengen gibt, wird in der Mengenlehre kontrovers diskutiert; ebenso mag man sich über unfundiertes Wissen und unfundierte Wirkungen streiten. Anders jedoch als in diesen Fällen, wo es um die Existenz von abstrakten Objekten geht, verhält es sich bei Sachverhalten oder Propositionen oder Aussageinhalten. Objekte existieren oder existieren nicht. Sachverhalte hingegen sind der Fall oder nicht der Fall; sie bestehen als Tatsachen oder bestehen nicht. Ihre Existenz, wenn man von einer solchen reden will, ist ihr bloßes Bestehen-oder-nicht-Bestehen. Für die so verstandene Existenz von Sachverhalten aber gilt dann: esse est concipi posse. Wenn man einen Sachverhalt konzipiert hat, hat man ihn schon in die Welt gesetzt, und die Frage ist »nur« noch, ob er als Tatsache besteht oder nicht. Wenn wir also unfundierte Aussageinhalte am logischen Reißbrett als Möglichkeiten entwerfen, so gibt es sie ipso facto wirklich, und wir müssen diese Ausgeburten unserer logischen Phantasie nur noch alethisch bewerten, als wahr oder falsch.
Machen wir uns also an die Arbeit. Parallel zu dem mengentheoretischen Objekt Ω
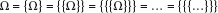
konzipieren wir einen einfachen aussagenlogischen Inhalt ν, die Negation ihrer selbst (statt des Gleichheitszeichens müssen wir hier, weil wir einen Aussageinhalt bestimmen wollen, das Bikonditional verwenden). Für ν gilt in quasidefinitorischer Weise:

Wenn Ω ein denkbares, konzipierbares Gebilde ist, was ja niemand bestreitet, dann muss auch ν ein denkbares Gebilde sein. Da aber ν ein Aussageinhalt ist, genügt seine Denkbarkeit für seine Existenz. Das Problem mit ν ist dann freilich, dass es sich um einen widerspruchsvollen Inhalt handelt, ja sogar um einen unbehebbar widerspruchsvollen, antinomischen Inhalt, denn ν besteht als Tatsache dann und nur dann, wenn ν nicht als Tatsache besteht.
Normalerweise, wenn wir uns in einen Widerspruch verwickeln, negieren wir eine der beiden widerstreitenden Seiten oder, wenn wir nicht entscheiden können, welche Seite zu inkriminieren ist, einstweilen die ganze Kontradiktion:

Aber im Fall der Negation-ihrer-selbst ist uns dieser Ausweg verbaut. Denn wenn wir sie negieren, bekräftigen wir sie, da sie selber schon ihre eigene Negation ist. Wir sind in ihrem Widerspruch gefangen. Das ist zutiefst beunruhigend, weil mit einem Mal die klassische Logik ins Wanken gerät. Wir haben einen unbehebbaren Widerspruch, die Antinomie der Negation, konzipiert und erfasst und uns denkend darin verfangen. Damit scheint das Nichtwiderspruchsprinzip außer Kraft gesetzt worden zu sein. Spekulative Hegel’sche Gedankenfiguren lassen von gar nicht mehr so ferne grüßen, so das Andere seiner selbst oder die absolute Negation, als welche Hegel das Wesen fasst. Doch heben wir uns die Beunruhigung für später auf, und wenden uns unterdessen Naheliegendem zu: unfundierten Aussagen im Allgemeinen.
Ein separates Zeichen für die Affirmation eines Satzes (wie vordem Freges Urteilsstrich) ist nicht mehr in Gebrauch; denn es genügtja, einen Satz auszusprechen oder aufzuschreiben, um ihn zu behaupten. Aber die doppelte Verneinung ist der Affirmation äquivalent, und so können wir die Affirmation ihrer selbst oder die unfundierte Affirmation andeuten, indem wir das Negationszeichen doppelt nehmen und als verdoppeltes vor eine leere Klammer schreiben:
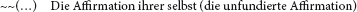
An die Stelle der drei Punkte in der Klammer ist in Gedanken der ganze Ausdruck zu setzen, wie es ja auch bei der unfundierten Negation und bei der Einermenge ihrer selbst der Fall war. Demgemäß können wir die Affirmation ihrer selbst (oder unfundierte Affirmation) nach dem Muster der Entwicklung von Ω und ν ins Endlose entwickeln:
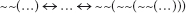
Um eine bequeme Schreibweise für unfundierte Aussagen einzuführen, wollen wir nun folgende Verabredung treffen. Wir setzen einen Ausdruck für eine unfundierte Aussage, der die drei Punkte als Auslassungszeichen enthält, in eckige Klammern, um anzuzeigen, was jeweils genau an die Stelle der drei Punkte einzusetzen ist: nämlich alles, was zwischen den eckigen Klammern steht. So erhalten wir als Andeutung der unfundierten Affirmation folgendes Satzgebilde:
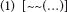
Die mit (1) angedeutete Aussage affirmiert nur sich selbst; das ist ihr ganzer Inhalt. Kennen wir einen solchen Denkinhalt aus anderen Zusammenhängen? Ja, und zwar aus ganz verschiedenen Zusammenhängen. Wir kennen ihn zum einen aus der Philosophiegeschichte in der eindrucksvollen Gestalt der Fichte’schen Tathandlung, durch die das Ich sich selber setzt, lateinisch: ponit, d. h. affirmiert. Wir kennen ihn ferner in der Gestalt der Reflexions-bestimmung der Identität, wie Hegel sie zu Beginn seiner Logik des Wesens betrachtet. Wir kennen ihn aber drittens sogar in einer umgangssprachlichen, harmlos-spielerischen Version, nämlich in Gestalt des sogenannten Wahrsagers, d. h. eines Satzes, mittels dessen seine eigene Wahrheit ausgesagt wird:
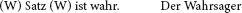
Spätestens jetzt wird klar, dass wir auch die Negation ihrer selbst nicht nur als Hegel’sches Selbstverhältnis der Negation (zum Beispiel als die Reflexionsbestimmung des Unterschiedes) oder als Heideggers nichtendes Nichts kennen, sondern ebenfalls in einer spielerischen, wenn auch keineswegs harmlosen Variante, nämlich in Gestalt des sogenannten Lügners, d. h. eines Satzes, mittels dessen seine eigene Unwahrheit ausgesagt wird:
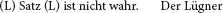
Aber lassen wir diese Entdeckung einstweilen auf sich beruhen und wenden uns wieder der unfundierten Affirmation zu, und zwar in der Formulierung (1), die kein wirklicher, sondern nur angedeuteter Satz ist, weil sie eine Leerstelle enthält, die durch sie selber gefüllt werden müsste: »[~~(…)]«. Da sich aber zwei hintereinander geschachtelte Negationszeichen neutralisieren oder aufheben, könnte man die unfundierte Affirmation auch ganz einfach ohne Negationszeichen aufschreiben:
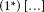
Dies ist nur eine Schreibvariante von (1), daher gilt die Äquivalenz:
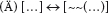
(Bei (1*) wissen wir allerdings nicht recht, wie wir diesen Satz ins Unendliche entwickeln sollten. Wenn wir Klammern einfügen, die ja nichts am Sinn ändern: »[(…)]«, dann vielleicht zu der Endlosformel: »(((…)))«.)
Für die Andeutung der Negation-ihrer-selbst brauchen wir statt eines doppelten Negationszeichens nur ein einfaches Negationszeichen. Dies ergibt die satzandeutende Formulierung:

Wenn wir nun die unfundierte Affirmation und die unfundierte Negation durch Entwicklung der sie definierenden Äquivalenzen näher bestimmen, zeigt sich Erstaunliches: Die Entwicklung würde für die unfundierte Affirmation und für die unfundierte Negation im Unendlichen zu identischen Formulierungen führen (denn die Klammern sind hier letztlich überflüssig):
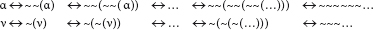
Der Wahrsager und der Lügner, Affirmation und Negation, sind also näher miteinander verwandt, als es auf den ersten Blick scheint. Das ist massiv untertrieben formuliert: Wahrsager und Lügner – die reine Affirmation und die reine Negation – sind, vollständig entwickelt, äquivalent. Wiederum schwankt der feste Boden der Logik unter uns, wie er schon schwankte, als wir auf die Antinomie der reinen unfundierten Negation stießen. Aber nun sieht man, dass selbst die heroische Maßnahme nichts nützen würde, die Parmenides angesichts der Antinomie der Negation ergriff: die Negation aus dem logischen Raum zu verbannen und nur das affirmative Sein zuzulassen. Denn die Affirmation selber ist, wie Hegel gegen Parmenides zu Recht geltend macht, in ihrem Kern der Negation äquivalent und jedenfalls nicht ohne diese denkbar. Das eleatische Opfer der Negation, des Unterschiedes, der Vielheit und des Werdens war ganz umsonst.
Unter einer anderen Betrachtung erweist sich die Affirmation allerdings auch als nicht äquivalent mit der Negation. Denn die Entwicklung obiger Äquivalenzen zeigt auch, dass sich die unfundierte Affirmation nur durch eine massive, sinnberührende Abstraktion aus der unfundierten Negation gewinnen bzw. wiederherstellen lässt. Man tut dabei nämlich so, als könnte man unendlich viele Negationszeichen paarweise ohne Rest zusammenfassen (was aber nur für geradzahlig endlich viele Negationszeichen möglich ist). So bekommt plötzlich der Anfang der Hegel’schen Logik eine unerwartete Brisanz und Beglaubigung, der ja Kontradiktorisches besagt: (a) Sein = Nichts; (b) Sein ≠ Nichts.
Doch schauen wir uns auch kurz noch die zweistelligen Wahrheitsfunktionen an. Wir können ohne Weiteres die Konjunktion ihrer selbst und ihrer selbst, kurz die Eigenkonjunktion, und ebenso die Eigenalternation (mit einschließendem »oder«), die Eigendisjunktion (mit ausschließendem »oder«), das Eigenkonditional, die Eigenkontradiktion und das Eigen-Tertium-non-datur bilden (stets ist der Ausdruck in eckigen Klammern in Gedanken an die Stelle der drei Punkte zu setzen):
| (3) | [(…) und (…)] | Eigenkonjunktion |
| (4) | [(…) oder (…)] | Eigenalternation |
| (5) | [entweder (…) oder (…), aber nicht beide] | Eigendisjunktion |
| (6) | [wenn (…), so (…)] | Eigenkonditional |
| (7) | [(…) und ~(…)] | Eigenkontradiktion |
| (8) | [(…) oder ~(…)] | Eigen-Tertium-non-datur |
Neben diesen total unfundierten Aussagen gibt es auch partiell fundierte, aber nicht wohlfundierte, wie etwa die folgenden (wobei der Schemabuchstabe »p« irgendeinen fundierten Aussagesatz vertritt):
| (9) | [(…) und p] |
| (10) | [(…) oder p] |
Was die semantische Bewertung dieser Sätze (als wahr oder falsch) angeht, so gilt folgendes. Für (1), (3) und (4) – Eigenaffirmation, Eigenkonjunktion und Eigenalternation – ergibt sich ein unklarer Befund. Wir können ohne Widerspruch annehmen, dass sie wahr sind, und ohne Widerspruch annehmen, dass sie falsch sind. Aber wir finden keinen Grund, diesen Sätzen verschiedene Wahrheitswerte zuzuordnen. Entweder sind sie alle wahr oder alle falsch, also jedenfalls paarweise logisch äquivalent, drücken also (bis auf Äquivalenz) dasselbe aus, und zwar wie schon Satz (1) die Affirmation ihrer selbst oder die reine, unfundierte Affirmation.
Die Sätze (6) und (8) – Eigenkonditional und Eigen-Tertiumnon-datur – sind auf jeden Fall wahr, logische Wahrheiten, also einander logisch äquivalent, wie man leicht erkennt, wenn man den Satz (6) so variiert:
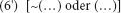
woraus sich durch Umstellung der Alternationsglieder Satz (8) ergibt.
(5) und (7) – Eigendisjunktion und Eigenkontradiktion – sind falsch, logische Falschheiten, also logisch äquivalent. Sie drücken den reinen Widerspruch aus.3 Ihre Negationen
| (11) | ~[entweder (…) oder (…), aber nicht beide] |
| (12) | ~[(…) und ~(…)] |
sind daher logisch wahr. (Man beachte, dass das äußere Negationszeichen hier jeweils außerhalb der eckigen Klammern steht und daher nicht an die Leerstellen miteingesetzt wird.)
Aus dem partiell unfundierten Satz (9) folgt »p« (bzw. der Satz, der für den Schemabuchstaben »p« eingesetzt wird); und der ebenfalls partiell unfundierte Satz (10) ist jedenfalls dann wahr, wenn »p« wahr ist. Folgende Satzschemata drücken daher logische Wahrheiten aus:
| (13) | Wenn [(…) und p], so p |
| (14) | Wenn p, so [(…) oder p] |
Nun aber kommen wir zu guter Letzt wieder zu unserem alten Bekannten, dem Lügner, zurück, hier zu Satz (2). Bisher verlief die semantische Bewertung undramatisch. Wir hatten einige logische Wahrheiten: (6), (8), (11), (12), (13), (14), einige logische Falschheiten: (5), (7), und einige logisch unentscheidbare Sätze: (1), (3), (4), (9), (10), und von den logischen Falschheiten konnten wir uns bequem distanzieren, indem wir sie negierten und uns an die Negationen, (11) und (12), hielten.
Doch der Lügner verneint sich selbst: »[~(…)]«. Wenn er wahr ist, gilt, was er ausdrückt, d. h., es gilt seine Verneinung; also ist er falsch. Wenn er aber falsch ist, gilt seine Verneinung, also wiederum er selber; also ist er wahr. Gerne würden wir uns von ihm distanzieren, indem wir uns an seine Negation hielten:
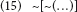
Aber diese Negation (nicht zu verwechseln mit Satz (1), der Affirmation ihrer selbst) ist mit ihm äquivalent, es gilt also:
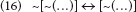
Unser Problem ist, dass es keine Möglichkeit gibt, uns von dem widerspruchsvollen Satz (2) oder von seiner ebenso widerspruchsvollen Negation (15) zu distanzieren. Wir haben eine echte Antinomie, d. h. einen prinzipiell unbehebbaren Widerspruch gefunden.
Was drückt diese Antinomie aus? In ihrer umgangssprachlichen Formulierung (»Dieser Satz ist nicht wahr«) ist zwar von einem Satz und von Wahrheit die Rede, aber das dient nur dem semantischen Aufstieg, ist nur äußeres Hilfsmittel des sprachlichen Ausdrucks. Worauf es ankommt, zeigt die Formulierung (2): Die Lügnerantinomie drückt (abgesehen vom Hilfsmittel des semantischen Aufstiegs) reine Negation oder Negativität aus, nichts sonst, also einen rein negativen Sachverhalt unterhalb der Gliederung des Satzes (in Subjekt und Prädikat), einen Sachverhalt, den wir ebenso gut das (reine) Nichts nennen könnten. Das Nichts (wenn wir denn so reden wollen) verwickelt uns, indem wir es denkend erfassen, in einen unaufhebbaren Widerspruch, eine Antinomie.
Wenn der Lügner umgangssprachlich formuliert wird, d. h. mittels semantischen Aufstiegs, bietet sich das semantische Prädikat »ist wahr« als die vermeintliche Quelle der Antinomie dar und zieht deswegen seit langem schon das Gros der logischen Reparaturarbeiten auf sich. Aber das Wahrheitsprädikat ist nur der Bote der logischen Katastrophe, nicht deren Ursache, oder vielmehr nur das technische Hilfsmittel für ihre sprachliche Formulierung. Die Quelle des Ungemachs ist das Zusammentreffen von Unfundiertheit und Negation, und dieses Zusammentreffen kann nicht verhindert werden, solange wir einerseits die Negation, etwa in negativen Sätzen, und andererseits unfundierte Strukturen verstehen. Und wir verstehen beides. Nur weil wir den Lügner bereits verstanden haben, finden wir ihn furchtbar und würden ihn lieber nicht verstehen wollen; aber dann ist es natürlich zu spät.
Wenn wir intellektuell redlich sein wollen, müssen wir anerkennen: Das Nichtwiderspruchsprinzip der klassischen Logik ist verletzt. Diese meines Erachtens unumstößliche Behauptung nenne ich die Antinomiethese. Das Nichtwiderspruchsprinzip ist verletzt, obwohl es qua Prinzip der klassischen Logik nicht verletzt werden soll und nicht preisgegeben werden darf, denn es gibt weit und breit nichts Evidenteres und epistemisch Wertvolleres als die klassische Logik in ihrer monumentalen Einfachheit und Eleganz. Die beiden großen Prinzipien der klassischen Logik, das Nichtwiderspruchsprinzip (»~(p ∧ ~p)«) und das Tertium non datur (»p ∨ ~p«), werden – das wollen wir uns nicht ausreden lassen – durch faktische Verletzungen nicht widerlegt und erweisen sich darin als normative oder regulative, nicht schlechthin konstitutive Prinzipien des Denkens und des Seins und als Verwandte der moralischen Prinzipien, die ebenfalls durch ihre Verletzungen nicht widerlegt werden. Widersprüche und Wahrheitswertlücken sollen nicht sein, weder sprachseitig noch weltseitig.
Der Lügner bezieht sich wesentlich auf sich selbst; es gibt ihn nicht unabhängig von seinem Selbstbezug. Darin gleicht er (wie alle unfundierten Aussageinhalte) dem Kierkegaard’schen Verhältnis, das sich zu sich selbst verhält. Das ist kein Zufall. Vielmehr kann man mit Hegel und mit Sartre die These wagen (wenn auch hier nicht mehr begründen), dass der Abgrund oder der Zirkel des Negativen die Quelle aller Selbstverhältnisse und des Bewusstseins ist.
1 Søren Kierkegaard, Die Krankheit zum Tode, Düsseldorf 1954, 8.
2 Jean-Paul Sartre, L’être et le néant. Essai d’ontologie phénoménologique, o. Ort [Paris] 1943, 20.
3 Ich ergreife die Gelegenheit zu einer Selbstkorrektur. In meinem Versuch über Wahrheit und Zeit, Paderborn 2006, 288, wird zwar nicht ausdrücklich gesagt, aber durch den Kontext der Anschein geweckt, die Eigenkontradiktion sei nicht nur widerspruchsvoll und daher falsch, sondern auch antinomisch wie die Eigennegation. Das war ein bedauerliches Versehen.