© Springer Nature Switzerland AG 2019
C. Bocci, L. ChiantiniAn Introduction to Algebraic Statistics with TensorsUNITEXT118https://doi.org/10.1007/978-3-030-24624-2_10

10. Projective Maps and the Chow’s Theorem

Cristiano Bocci1   and Luca Chiantini1
(1)
Dipartimento di Ingegneria dell’Informazione e Scienze Matematiche, Università di Siena, Siena, Italy
 
 
Cristiano Bocci
Email: cristiano.bocci@unisi.it

The chapter contains the proof of the Chow’s Theorem, a fundamental result for algebraic varieties with an important consequence for the study of statistical models. It states that, over an algebraically closed field, like $$\mathbb C$$, the image of a projective (or multiprojective) variety X under a projective map is a Zariski closed subset of the target space, i.e., it is itself a projective variety.

The proof of Chow’s Theorem requires an analysis of projective maps, which can be reduced to a composition of linear maps, Segre maps and Veronese maps.

The proof also will require the introduction of a basic concept of the elimination theory, i.e., the resultant of two polynomials.

10.1 Linear Maps and Change of Coordinates

We start by analyzing projective maps induced by linear maps of vector spaces.

The nontrivial case concerns linear maps which are surjective but not injective. After a change of coordinates, such maps induce maps between projective varieties that can be described as projections .

Despite the fact that the words projective and projection have a common origin (in the paintings of the Italian Renaissance, e.g.) projections not always give rise to projective maps.

The description of the image of a projective variety under projections relies indeed on nontrivial algebraic tools: the rudiments of the elimination theory.

Let us start with a generalization of Example 9.​3.​3.

Definition 10.1.1

Consider a linear map $$\phi :\mathbb C^{n+1}\rightarrow \mathbb C^{m+1}$$ which is injective.

Then $$\phi $$ defines a projective map (which, by abuse, we will still denote by $$\phi $$) between the projective spaces $$\mathbb P^n\rightarrow \mathbb P^m$$, as follows:

– for all $$P\in \mathbb P^n$$, consider a set of homogeneous coordinates $$[x_0 : \dots : x_n]$$ and send P to the point $$\phi (P)\in \mathbb P^m$$ with homogeneous coordinates $$[\phi (x_0,\dots ,x_n)]$$.

Such maps are called linear projective maps .

It is clear that the point $$\phi (P)$$ does not depend on the choice of a set of coordinates for P, since $$\phi $$ is linear.

Notice that we cannot define a projective map in the same way when $$\phi $$ is not injective. Indeed, in this case, the image of a point P whose coordinates lie in the Kernel of $$\phi $$ would be indeterminate.

Since any linear map $$\mathbb C^{n+1}\rightarrow \mathbb C^{m+1}$$ is defined by linear homogeneous polynomials, then it is clear that the induced map between projective spaces is indeed a projective map.

Example 10.1.2

Assume that the linear map $$\phi $$ is an isomorphism of $$\mathbb C^{n+1}$$. Then the corresponding linear projective map is called a change of coordinates .

Indeed $$\phi $$ corresponds to a change of basis inside $$\mathbb C^{n+1}$$.

The associated map $$\phi :\mathbb P^n\rightarrow \mathbb P^n$$ is an isomorphism, since the inverse isomorphism $$\phi ^{-1}$$ determines a projective map which is the inverse of $$\phi $$.

Remark 10.1.3

By construction, any change of coordinates in a projective space is a homeomorphism of the corresponding topological space, in the Zariski topology.

So, the image of a projective variety under a change of coordinates is still a projective variety.

From now on, when dealing with projective varieties, we will freely act with the change of coordinates on them.

The previous remark generalizes to any linear projective map.

Proposition 10.1.4

For every injective map $$\phi :\mathbb C^{n+1}\rightarrow \mathbb C^{m+1}$$, $$m\ge n$$, the associated linear projective map $$\phi :\mathbb P^n\rightarrow \mathbb P^m$$ sends projective subvarieties of $$\mathbb P^n$$ to projective subvarieties of $$\mathbb P^m$$.

In topological terms, any linear projective map is closed in the Zariski topology, i.e., it sends closed sets to closed sets.

Proof

The linear map $$\phi $$ factorizes in a composition $$\phi =\psi \circ \phi '$$ where $$\phi '$$ is the inclusion which sends $$[x_0:\dots :x_n]$$ to $$[x_0:\dots :x_n:0:\dots :0]$$, $$m-n$$ zeroes, and $$\psi $$ is a change of coordinates (notice that we are identifying the coordinates in $$\mathbb P^n$$ with the first $$n+1$$ coordinates in $$\mathbb P^m$$).

Thus, up to a change of coordinates, any linear projective map can be reduced to the map that embeds $$\mathbb P^n$$ into $$\mathbb P^m$$ as the linear space defined by equations $$x_{n+1}=\dots =x_m=0$$.

It follows that if $$X\subset \mathbb P^n$$ is the subvariety defined by homogeneous polynomials $$f_1,\dots ,f_s$$ then, up to a change of coordinates, the image of X is the projective subvariety defined in $$\mathbb P^m$$ by the polynomials $$f_1,\dots ,f_s,x_{n+1},\dots ,x_m$$.   $$\square $$

The definition of linear projective maps, which requires that $$\phi $$ is injective, becomes much more complicated if we drop the injectivity assumption.

Let $$\phi :\mathbb C^{n+1}\rightarrow \mathbb C^{m+1}$$ be a non injective linear map. In this case, we cannot define through $$\phi $$ a projective map $$\mathbb P^n\rightarrow \mathbb P^m$$ as above, since for any vector $$(p_0,\dots ,p_n)$$ in the kernel of $$\phi $$, the image of the point $$[p_0:\dots :p_n]$$ is undefined, because $$\phi (p_0,\dots ,p_n)$$ vanishes.

On the other hand, the kernel of $$\phi $$ defines a projective linear subspace of $$\mathbb P^n$$, the projective kernel , which will be denoted by $$K_\phi $$.

If $$X\subset \mathbb P^n$$ is a subvariety which does not meet $$K_\phi $$, then the restriction of $$\phi $$ to the coordinates of the points of X determines a well-defined map from X to $$\mathbb P^m$$.

Example 10.1.5

Consider the point $$P_0\in \mathbb P^m$$ of projective coordinates $$[1:0:0:\dots :0]$$ and let M be the linear subspace of $$\mathbb C^{m+1}$$ of the points with first coordinate equal to 0, i.e., $$M=X(x_0)$$. Let $$\phi _0:\mathbb C^{m+1}\rightarrow M$$ be the linear surjective (but not injective) map which sends a vector $$(x_0,x_1,\dots ,x_m)$$ to $$(0,x_1,\dots , x_m)$$.

Notice that M defines a linear projective subspace $$\mathbb P(M)\subset \mathbb P^m$$, of projective dimension $$m-1$$ (i.e., a hyperplane), and $$P_0\notin \mathbb P(M)$$. Moreover $$P_0$$ is exactly the projective kernel of $$\phi _0$$. Let Q be any point of $$\mathbb P^m$$ different from $$P_0$$. If $$Q=[q_0: q_1 :\cdots : q_m]$$ then $$\phi _0(Q)=(0,q_1,\dots , q_m)$$ determines a well defined projective point, which corresponds to the intersection of $$\mathbb P(M)$$ with the line $$P_0Q$$. This is the reason why we call $$\phi _0$$ the projection from $$P_0$$ to $$\mathbb P(M)$$ . Notice that we cannot define a global projection $$\mathbb P^m\rightarrow \mathbb P(M)$$, since it would not be defined in $$P_0$$. What we get is a set-theoretic map $$\mathbb P^m\setminus \{P_0\}\rightarrow \mathbb P(M)$$. For any other choice of a point $$P\in \mathbb P^m$$ and a hyperplane H, not containing P, there exists a change of coordinates which sends P to $$P_0$$ and H to $$\mathbb P(M)$$. Thus the geometric projection $$\mathbb P^m\setminus \{P\}\rightarrow H$$ from P to H is equal to the map described above, up to a change of coordinates.

We can generalize the construction to projections from positive dimensional linear subspaces.

Namely, for a fixed $$n<m$$ consider the subspace $$N\subset \mathbb C^{m+1}$$, of dimension $$m-n<m+1$$, formed by the $$(m+1)$$-tuples of type $$(0,\dots , 0, x_{n+1},\dots ,x_m)$$ and let M be the $$(n+1)$$-dimensional linear subspace of $$(m+1)$$-tuples of type $$(x_0,\dots ,x_n,0\dots ,0)$$. Let $$\phi _0:\mathbb C^{m+1}\rightarrow M$$ be the linear surjective (but not injective) map which sends any $$(x_0,\dots ,x_m)$$ to $$(x_1,\dots ,x_n,0,\dots , 0) $$.

Notice that N and M define disjoint linear projective subspaces, respectively $$\mathbb P(N)$$, of projective dimension $$m-n-1$$, and $$\mathbb P(M)$$, of projective dimension n. Let Q be a point of $$\mathbb P^m\setminus \mathbb P(N)$$ (this means exactly that Q has coordinates $$[q_0:\dots :q_n]$$, with $$q_i\ne 0$$ for some index i between 0 and n). Then the image of Q under $$\phi _0$$ is a well defined projective point, which corresponds to the intersection of $$\mathbb P(M)$$ with the projective linear subspace spanned by $$\mathbb P(N)$$ and Q. This is why we get from $$\phi _0$$ a set-theoretic map $$\mathbb P^m\setminus \mathbb P(N)\rightarrow \mathbb P(M)$$, which we call the projection from $$\mathbb P(N)$$ to $$\mathbb P(M)$$ .

For any choice of two disjoint linear subspaces $$L_1$$, of dimension $$m-n-1$$, and $$L_2$$, of dimension n,there exists a change of coordinates which sends $$L_1$$ to $$\mathbb P(N)$$ and $$L_2$$ to $$\mathbb P(M)$$. Thus the geometric projection $$\mathbb P^m\setminus L_1\rightarrow L_2$$ from $$L_1$$ to $$L_2$$ is equal to the map described above, up to a change of coordinates.

Example 10.1.6

Let $$\phi :\mathbb C^{m+1}\rightarrow \mathbb C^{n+1}$$ be any surjective map, with kernel $$L_1$$ (of dimension $$m-n$$). We can always assume, up to a change of coordinates, that $$L_1$$ coincides with the subspace N defined in Example 10.1.5. Then considering the linear subspace $$M\subset \mathbb C^{m+1}$$ defined in Example 10.1.5, we can find an isomorphism of vector spaces $$\psi $$ from M to $$\mathbb C^{n+1}$$ such that $$\phi =\psi \circ \phi _0$$, where $$\phi _0$$ is the map introduced in Example 10.1.5. Thus, after an isomorphism and a change of coordinates, $$\phi $$ acts on points of $$\mathbb P^m\setminus K_\phi $$ as a geometric projection.

Example 10.1.6 suggests the following definition.

Definition 10.1.7

Given a linear surjective map $$\phi :\mathbb C^{m+1}\rightarrow \mathbb C^{n+1}$$ and a subvariety $$X\subset \mathbb P^m$$ which does not meet $$K_\phi $$, the restriction map $$\phi _{|X}:X\rightarrow \mathbb P^n$$ is a well defined projective map, which will be denoted as a projection of X from $$K_\phi $$. The subspace $$K_\phi $$ is also called the center of the projection.

Notice that $$\phi _{|X}$$ is a projective map, since it is defined, up to isomorphisms and change of coordinates, by (simple) homogeneous polynomials (see Exercise 31).

Thus, linear surjective maps define projections from suitable subvarieties of $$\mathbb P^m$$ to $$\mathbb P^n$$. Next section is devoted to prove that projections are closed, in the Zariski topology.

10.2 Elimination Theory

In this section, we introduce the basic concept of the elimination theory: the resultant of two polynomials.

The resultant provides an answer to the following problem:

– assume we are given two (not necessarily homogeneous) polynomials $$f,g\in \mathbb C[x]$$. Clearly both f and g factorize in a product of linear factors. Which algebraic condition must f, g satisfy to share a common factor, hence a common root?

Definition 10.2.1

Let f, g be nonconstant (nonhomogeneous) polynomials in one variable x, with coefficients in $$\mathbb C$$. Write $$f= a_0+a_1x+a_2x^2+\dots +a_nx^n$$ and $$g=b_0+b_1x+b_2x^2+\dots +b_mx^m$$. The resultant  R(f, g) of f, g is the determinant of the Sylvester matrix  S(f, g), which in turn is the $$(m+n)\times (m+n)$$ matrix defined as follows:
$$ S(f,g) = \det \begin{pmatrix} a_0 &{} a_1 &{} a_2 &{} \dots &{} a_n &{} 0 &{} 0 &{} 0 &{} \dots &{} 0 \\ 0 &{} a_0 &{} a_1 &{} a_2 &{} \dots &{} a_n &{} 0 &{} 0 &{} \dots &{} 0 \\ \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots \\ 0 &{} \dots &{} 0 &{} 0 &{} 0 &{} a_0 &{} a_1 &{} a_2 &{} \dots &{} a_n \\ b_0 &{} b_1 &{} \dots &{} b_m &{} 0 &{} 0 &{} 0 &{} 0 &{} \dots &{} 0 \\ 0 &{} b_0 &{} b_1 &{} \dots &{} b_m &{} 0 &{} 0 &{} 0 &{} \dots &{} 0 \\ \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots &{} \dots \\ 0 &{} \dots &{} 0 &{} 0 &{} 0 &{} 0 &{} b_0 &{} b_1 &{} \dots &{} b_m \end{pmatrix} $$
where the a’s are repeated m times and the b’s are repeated n times.

Notice that when f is constant and g has degree $$d>0$$, then by definition $$R(f,g)=f^d$$.

When both f, g are constant, the previous definition of resultant makes no sense. In this case we set:
$$ R(f,g)={\left\{ \begin{array}{ll} 0 &{}\text { if } f=g=0 \\ 1 &{}\text { otherwise. }\end{array}\right. } $$

Example 10.2.2

Just to give an instance, if $$f=x^2-3x+2$$ and $$g= x-1$$ (both vanishing at $$x=1$$), the resultant R(f, g) is
$$ R(f,g) = \det S(f,g)= \det \begin{pmatrix} 1 &{} -3 &{} 2 \\ 1 &{} -1 &{} 0 \\ 0 &{} 1 &{} -1 \end{pmatrix} = 0 $$

Proposition 10.2.3

With the previous notation, f and g have a common root if and only if $$R(f,g)=0$$.

Proof

The proof is immediate when either f or g are constant (Exercise 33).

Otherwise write $$\mathbb C[x]_i$$ for the vector space of polynomials of degree $$\le i$$ in $$\mathbb C[x]$$. Then the transpose of S(f, g) is the matrix of the linear map:
$$ \phi : \mathbb C[x]_{m-1}\times \mathbb C[x]_{n-1}\rightarrow \mathbb C[x]_{m+n-1} $$
which sends (p, q) to $$pf+qg$$ (matrix computed with respect to the natural basis defined by the monomials). Thus $$R(f,g)=0$$ if and only if the map has a nontrivial kernel.

Let $$(p_0,q_0)$$ be a nontrivial element of the kernel, i.e., $$p_0f+q_0g=0$$. Consider the factors $$(x-\alpha _i)$$ of f, where the $$\alpha _i$$’s are the roots of f (possibly some factor is repeated). Then, all these factors must divide $$q_0g$$. Since $$\deg q_0<\deg f$$, at least one factor $$x-\alpha _i$$ must divide g. Thus $$\alpha _i$$ is a common root of f and g.

Conversely, if $$\alpha $$ is a common root of f and g, then $$x-\alpha $$ divides both f and g. Hence setting $$p_0=g/(x-\alpha )$$, $$q_0=-f/(x-\alpha )$$, one finds a nontrivial element $$(p_0,q_0)$$ of the kernel of $$\phi $$, so that $$\det S(f,g)=0$$.   $$\square $$

We have the analogue construction if f, g are homogeneous polynomials in two or more variables.

Definition 10.2.4

If f, g are homogeneous polynomials in $$\mathbb C[x_0,x_1, \dots , x_r]$$ one can define the 0th resultant $$R_0(f,g)$$ of f, g just by considering f and g as polynomials in $$x_0$$, with coefficients in $$\mathbb C[x_1,\dots ,x_r]$$, and taking the determinant of the corresponding Sylvester matrix $$S_0(f,g)$$.

$$R_0(f,g)$$ is thus a polynomial in $$x_1,\dots ,x_r$$.

For instance, if $$f=x_0^2x_1+x_0x_1x_2+x_2^3$$ and $$g= 2x_0x_1^2+x_0x_2^2 + 3 x_1^2x_2$$, then the 0th resultant is:
$$\begin{aligned} R_0(f,g) = \det S_0(f,g)&= \det \begin{pmatrix} x_1 &{} x_1x_2 &{} x_2^3 \\ 2x_1^2+x_2^2 &{} 3x_1^2x_2 &{} 0 \\ 0 &{} 2x_1^2+x_2^2 &{} 3x_1^2x_2 \end{pmatrix} = \\&\qquad \quad = 3x_1^5x_2^2+4x_1^4x_2^3-3x_1^3x_2^4+4x_1^2x_2^5+x_2^7. \end{aligned}$$
From Proposition 10.2.3, with an easy induction on the number of variables, one finds that the resultant of homogeneous polynomials in several variables has the following property:

Proposition 10.2.5

Let f, g be homogeneous polynomials in $$\mathbb C[x_0,x_1, \dots , x_r]$$. Then $$R_0(f,g) $$ vanishes at $$(\alpha _1,\dots ,\alpha _r)$$ if and only if there exists $$\alpha _0\in \mathbb C$$ with:
$$ f(\alpha _0,\alpha _1,\dots ,\alpha _r) = g(\alpha _0,\alpha _1,\dots ,\alpha _r)=0. $$

Less obvious, but useful, is the following remark on the resultant of two homogeneous polynomials.

Proposition 10.2.6

Let f, g be homogeneous polynomials in $$\mathbb C[x_0,x_1, \dots , x_r]$$. Then $$R_0(f,g) $$ is homogeneous.

Proof

The entries $$s_{ij}$$ of the Sylvester matrix $$S_0(f,g)$$ are homogeneous and their degrees decrease by 1 passing from one element $$s_{ij}$$ to the next element $$s_{ij+1}$$ in the same row (unless some of them is 0). Thus for any nonzero entry $$s_{ij}$$ of the matrix, the number $$\deg s_{ij}-j$$ depends only on the row i. Call it $$u_i$$. Then the summands given by any permutation, in the computation of the determinant, are homogeneous of same degree:
$$ d=\frac{1}{2} (n+m+1)(n+m)+ \sum _i u_i, $$
so that $$R_0(f,g)$$ is homogeneous, and its degree is equal to d.   $$\square $$

Next, a fundamental property of the resultant $$R_0(f,g)$$ is that it belongs to the ideal generated by f and g. We will not give a full proof of this property, and refer to the book [1] for it.

Instead, we just prove that $$R_0(f,g)$$ belongs to the radical of the ideal generated by f and g, which is sufficient for our aims.

Proposition 10.2.7

Let f, g be homogeneous polynomials in $$\mathbb C[x_0,x_1, \dots , x_r]$$. Then $$R_0(f,g) $$ belongs to the radical of the ideal generated by f and g.

Proof

In view of the Nullstellensatz, it is sufficient to prove that $$R_0(f,g)$$ vanishes at all points of the variety defined by f and g. But this is obvious from Proposition 10.2.5: if $$[\alpha _0:\alpha _1:\dots :\alpha _r]$$ are homogeneous coordinates of $$P\in V(f,g)$$, then
$$ R_0(f,g)(\alpha _0,\alpha _1,\dots ,\alpha _r)=R_0(f,g)(\alpha _1,\dots ,\alpha _r)=0, $$
since $$f(x_0,\alpha _1,\dots ,\alpha _r)$$ and $$g(x_0,\alpha _1,\dots ,\alpha _r)$$, polynomials in $$\mathbb C[x_0]$$, have a common root $$\alpha _0$$.   $$\square $$

10.3 Forgetting a Variable

In Sect. 10.1 we introduced the projection maps as projectifications of surjective linear maps $$\phi :\mathbb C^{m+1}\rightarrow \mathbb C^{n+1}$$. It is important to recall that when $$\phi $$ has nontrivial kernel (i.e., when $$n<m$$) the projection is not defined as a map between the two projective spaces $$\mathbb P^m$$ and $$\mathbb P^n$$. On the other hand, for any subvariety $$X\subset \mathbb P^m$$ which does not intersect the projectification of $$Ker (\phi )$$, the map $$\phi $$ corresponds to a well defined projective map $$X\rightarrow \mathbb P^n$$.

In this section, we describe the image of a variety in a projection $$\pi $$ from a point, i.e., when the center of projections has dimension 0. It turns out, in particular, that $$\pi (X)$$ is itself an algebraic variety.

Through this section, consider the surjective linear map $$\phi :\mathbb C^{m+1}\rightarrow \mathbb C^m$$ which sends $$(\alpha _0,\alpha _1,\dots ,\alpha _m)$$ to $$(\alpha _1,\dots ,\alpha _m)$$. The kernel of the map is generated by $$(1,0,\dots ,0)$$. Thus, if X is a projective variety in $$\mathbb P^m$$ which misses the point $$P_0=[1:0:\dots :0]$$, then the map induces a well defined projective map $$\pi :X\rightarrow \mathbb P^{m-1}$$: the projection from $$P_0$$ (see Definition 10.1.7).

For any point $$Q\in \pi (X)$$, $$Q=[q_1:\dots :q_n]$$, the inverse image of Q in X is the the intersection of X with the line joining $$P_0$$ and Q. Thus $$\pi ^{-1}(Q)$$ is the set of points in X with coordinates $$[q_0:q_1:\dots :q_n]$$, for some $$q_0\in \mathbb C$$.

Remark 10.3.1

For all $$Q\in \pi (X)$$, the inverse image $$\pi ^{-1}(Q)$$ is finite.

Indeed $$\pi ^{-1}(Q)$$ is a Zariski closed set in the line $$P_0Q$$, and it does not contain $$P_0$$, since $$P_0\notin X$$. The claim follows since the Zariski topology on a line is the cofinite topology.

Let $$J\subset \mathbb C[x_0,\dots ,x_n]$$ be the homogeneous ideal associated to X. Define:
$$ J_0=J\cap \mathbb C[x_1,\dots ,x_n]. $$
In other words, $$J_0$$ is the set of elements in J which are constant with respect to the variable $$x_0$$. In Chap. 13 we will talk again about Elimination Theory, but from the point of view of Groebner Basis; there, the ideal $$J_0$$ will be called the first elimination ideal  of J (Definition 13.​5.​1).

Remark 10.3.2

$$J_0$$ is a homogeneous radical ideal in $$\mathbb C[x_1,\dots ,x_n]$$.

Indeed $$J_0$$ is obviously an ideal. Moreover for any $$g\in J_0$$, any homogeneous component $$g_d$$ of g belongs to J, because J is homogeneous, and does not contain $$x_0$$. Thus $$g_d\in J_0$$, and this is sufficient to conclude that $$J_0$$ is homogeneous (see Proposition 9.​1.​15).

If $$g^d\in J_0$$ for some $$g\in \mathbb C[x_1,\dots ,x_n]$$, then $$g\in J$$, because J is radical, moreover g does not contain $$x_0$$. Thus also $$g\in J_0$$.

We prove that $$\pi (X)$$ is the projective variety defined by $$J_0$$. We will need the following refinement of Lemma 9.​1.​5:

Lemma 10.3.3

Let $$Q_1,\dots ,Q_k$$ be a finite set of points in $$\mathbb P^n$$. Then there exists a linear form $$\ell \in \mathbb C[x_0,\dots ,x_n]$$ such that $$\ell (Q_i)\ne 0$$ for all i.

If none of the $$Q_i$$’s belong to the variety defined by a homogeneous ideal J, then there exists $$g\in J$$ such that $$g(Q_i)\ne 0$$ for all i.

Proof

Fix a set of homogeneous generators $$g_1,\dots g_s$$ of J.

First assume that all the $$g_i$$’s are linear. Then the $$g_i$$’s define a subspace L of the space of linear homogeneous polynomials in $$\mathbb C[x_0,\dots ,x_n]$$. For each $$Q_i$$, the set $$L_i$$ of linear forms in L that vanish at $$Q_i$$ is a linear subspace of L, which is properly contained in L, because some $$g_j$$ does not vanish at $$Q_i$$. Since a nontrivial complex linear space cannot be the union of a finite number of proper subspaces, we get that for a general choice of $$b_1,\dots ,b_s\in \mathbb C$$, the linear form $$\ell =b_1g_1+\dots + b_sg_s$$ does not belong to any $$L_i$$, thus $$\ell (Q_i)\ne 0$$ for all i. This proves the second claim for ideals generated by linear forms.

The first claim now follows soon, since the (irrelevant) ideal J generated by all the linear forms defines the empty set.

For general $$g_1,\dots ,g_s$$, call $$d_i$$ the degree of $$g_i$$ and $$d=\max \{d_i\}.$$ If $$\ell $$ is a linear form that does not vanish at any $$Q_i$$, then $$h_j=\ell ^{d-d_j}g_j$$ is a form of degree d that vanishes at $$Q_i$$ precisely when $$g_j$$ vanishes. The forms $$h_1,\dots , h_s$$ define a subspace $$L'$$ of the space of forms of degree d. For all i, the set of forms in $$L'$$ that vanish at $$Q_i$$ is a proper subspace of $$L'$$. Thus, as before, for a general choice of $$b_1,\dots ,b_s\in \mathbb C$$, the form $$g=b_1h_1+\dots + b_sh_s$$ is an element of J which does not vanish at any $$Q_i$$.   $$\square $$

Theorem 10.3.4

The variety defined in $$\mathbb P^{n-1}$$ by the ideal $$J_0$$ coincides with $$\pi (X)$$.

Proof

Let $$Q\in \pi (X)$$, $$Q=[q_1:\dots :q_n]$$. Then there exists $$q_0\in \mathbb C$$ such that the point $$P=\pi ^{-1}(Q)=[q_0:q_1:\dots :q_n]\in \mathbb P^n$$ belongs to X. Thus $$g(P)=0$$ for all $$g\in J$$. In particular, this is true for all $$g\in J_0$$. On the other hand, if $$g\in J_0$$ then g does not contain $$x_0$$, thus:
$$ 0 = g(P)=g(q_0,q_1,\dots ,q_n)=g(q_1,\dots ,q_n)=g(Q). $$
This proves that the variety defined by $$J_0$$ contains $$\pi (X)$$.

Conversely, identify $$\mathbb P^{n-1}$$ with the hyperplane $$x_0=0$$, and fix a point $$Q =[q_1:\dots :q_n]\notin \pi (X)$$. Consider an element $$f\in J$$ that does not vanish at $$P_0$$ and let W be the variety defined by f. The intersection of W with the line $$P_0Q$$ is a finite set $$Q_1,\dots , Q_k$$. Moreover no $$Q_i$$ can belong to X, since $$\pi ^{-1}(Q)$$ is empty. Thus, by Lemma 10.3.3, there exists $$g\in J$$ that does not vanish at any $$Q_i$$. Consider the resultant $$h=R_0(f,g)$$. By Proposition 10.2.7, h belongs to the radical of the ideal generated by f, g, thus it belongs to J, which is a radical ideal. Moreover h does not contain the variable $$x_0$$. Thus $$h\in J_0$$. Finally, from Proposition 10.2.5 it follows that $$h(Q)\ne 0$$. Then Q does not belong to the variety defined by $$J_0$$.   $$\square $$

Remark 10.3.5

A direct consequence of Theorem 10.3.4 is that the projection $$\pi $$ is a closed map, in the Zariski topology.

Indeed any closed subset Y of a projective variety X is itself a projective variety, thus by Theorem 10.3.4 the image of Y in $$\pi $$ is Zariski closed.

We can repeat all the constructions of this section by selecting any variable $$x_i$$ instead of $$x_0$$ and performing the elimination of $$x_i$$. Thus we can define the i -th resultant $$R_i(f,g)$$ and use it to prove that projections with center any coordinate point $$[0:\dots :0:1:0:\dots :0]$$ are closed maps.

10.4 Linear Projective and Multiprojective Maps

In this section, we prove that projective maps defined by linear maps of projective spaces are closed in the Zariski topology.

Remark 10.4.1

Let V, W be linear space, respectively, of dimension $$n+1,m+1$$.

The choice of a basis for V corresponds to fixing an isomorphism between V and $$\mathbb C^{n+1}$$. Thus we can identify, after a choice of the basis, the projective space $$\mathbb P(V)$$ with $$\mathbb P^n$$. We will use this identification to introduce all the concepts of Projective Geometry into $$\mathbb P(V)$$. Notice that two such identifications differ by a change of basis in $$\mathbb P^n$$, thus they are equivalent, up to an isomorphism of $$\mathbb P^n$$.

Similarly, the choice of a basis for W corresponds to fixing an isomorphism between W and $$\mathbb C^{m+1}$$.

A linear map $$W\rightarrow V$$ corresponds, under the choice of a basis, to a linear map $$\mathbb C^{m+1}\rightarrow \mathbb C^{n+1}$$. Thus, the study of projective maps in $$\mathbb P^m$$ and $$\mathbb P^n$$ induced by linear maps $$\mathbb C^{m+1}\rightarrow \mathbb C^{n+1}$$ corresponds to the study of projective maps in $$\mathbb P(W),\mathbb P(V)$$ induced by linear maps $$W\rightarrow V$$.

Proposition 10.4.2

Let $$\phi :\mathbb C^{m+1}\rightarrow \mathbb C^{n+1}$$ be a linear map. Let $$K_\phi $$ be the projective kernel of $$\phi $$ and let $$X\subset \mathbb P^m$$ be a projective subvariety such that $$X\cap K_\phi =\emptyset $$. Then $$\phi $$ induces a projective map $$X\rightarrow \mathbb P^n$$ (that we will denote again with $$\phi $$) which is a closed map in the Zariski topology.

Proof

The map $$\phi $$ factors through a linear surjection $$\phi _1:\mathbb C^{m+1}\rightarrow \mathbb C^{m+1}/Ker(\phi )$$ followed by a linear injection $$\phi _2$$. After the choice of a basis, the space $$\mathbb C^{m+1}/Ker(\phi )$$ can be identified with $$\mathbb C^{N+1}$$, where $$N=m-\dim (Ker(\phi ))$$, so that $$\phi _1$$ can be considered as a map $$\mathbb C^{m+1}\rightarrow \mathbb C^{N+1}$$ and $$\phi _2 $$ as a map $$\mathbb C^{N+1}\rightarrow \mathbb C^{n+1}$$. Since X does not meet the kernel of $$\phi _1$$, by Definition 10.1.7 $$\phi _1$$ induces a projection $$X\rightarrow \mathbb P^N$$. The injective map $$\phi _2$$ defines a projective map $$\mathbb P^N\rightarrow \mathbb P^n$$, by Definition 10.1.1. The composition of these two maps is the projective map $$\phi :X\rightarrow \mathbb P^n$$ of the claim. It is closed since it is the composition of two closed maps.   $$\square $$

Notice that the projective map $$\phi $$ is only defined up to a change of coordinate, since it relies on the choice of a basis in $$\mathbb C^{m+1}/Ker(\phi )$$.

The previous result can be extended to maps from multiprojective varieties to multiprojective spaces.

Example 10.4.3

Consider a multiprojective product $$\mathbb P^{a_1}\times \dots \times \mathbb P^{a_s}$$ and an injective linear map $$\phi :\mathbb C^{a_1+1}\rightarrow \mathbb C^{m+1}$$. Then the induced linear map:
$$ \mathbb P^{a_1}\times \mathbb P^{a_2}\times \dots \times \mathbb P^{a_s} \rightarrow \mathbb P^{m}\times \mathbb P^{a_2}\times \dots \times \mathbb P^{a_s} $$
is multiprojective and closed, because the product of closed maps is closed.

Of course, the same statement holds if we replace i with any index or if we mix up the indices. Moreover we can apply it repeatedly.

Similarly, consider a linear map $$\phi :\mathbb C^{a_1+1}\rightarrow \mathbb C^{m+1}$$ and a multiprojective subvariety $$X\subset \mathbb P^{a_1}\times \dots \times \mathbb P^{a_s}$$ such that X is disjoint from $$\mathbb P(\ker \phi )\times \mathbb P^{a_2}\times \dots \times \mathbb P^{a_s}$$. Then there is an induced linear map: $$X \rightarrow \mathbb P^{m}\times \mathbb P^{a_2}\times \dots \times \mathbb P^{a_s}$$ which is multiprojective and closed.

Proposition 10.4.4

Any projection $$\pi _i$$ from a multiprojective space $$\mathbb P^{a_1}\times \dots \times \mathbb P^{a_s}$$ to any of its factor $$\mathbb P^{a_i}$$ is a closed projective map.

Proof

The map $$\pi _i$$ is defined by sending $$P=([p_{10}:\dots :p_{1a_1}],\dots ,[p_{s0}:\dots :p_{sa_s}])$$ to $$[p_{i0}:\dots ,p_{ia_i}]$$. Thus the map is defined by multihomogeneous polynomials (of multidegree 1 in the ith set of variables and 0 in the other sets).

To prove that $$\pi _i$$ is closed, we show that the image in $$\pi _i$$ of any multiprojective variety is a projective subvariety of $$\mathbb P^{a_i}$$. Let $$X\subset \mathbb P^{a_1}\times \dots \times \mathbb P^{a_s}$$ be a multiprojective subvariety and let $$Y=\pi _i(X)$$. If $$Y=\mathbb P^{a_i}$$, there is nothing to prove. Thus the claim holds if $$n_i=0$$, i.e., $$\mathbb P^{a_i}$$ is a point. We will proceed then by induction on $$a_i$$, assuming that $$Y\ne \mathbb P^{a_i}$$.

Let Q be a point of $$\mathbb P^{a_i}\setminus Y$$. Then no points of type $$(P_1,\dots ,P_s)$$ with $$P_i=Q$$ can belong to X. Thus X does not contain points $$(P_1,\dots ,P_s)$$, with $$P_i$$ in the projective kernel of the projection from Q.

The claim now follows from Example 10.4.3.   $$\square $$

Corollary 10.4.5

Any projection $$\pi _i$$ from a multiprojective space $$\mathbb P^{a_1}\times \dots \times \mathbb P^{a_s}$$ to a product of some of its factors is a closed projective map.

10.5 The Veronese Map and the Segre Map

We introduce now two fundamental projective and multiprojective maps, which are the cornerstone, together with linear maps, of the construction of projective maps. The first map, the Veronese map, is indeed a generalization of the map built in Example 9.​1.​33.

We recall that a monomial is monic if its coefficient is 1.

Definition 10.5.1

Fix n, d and set $$N=\left( {\begin{array}{c}n+d\\ d\end{array}}\right) -1$$. There are exactly $$N+1$$ monic monomials of degree d in $$n+1$$ variables $$x_0,\dots , x_n$$. Let us call $$M_0,\dots , M_N$$ these monomials, for which we fixed an order.

The Veronese map  of degree d in $$\mathbb P^n$$ is the map $$v_{n,d}:\mathbb P^n\rightarrow \mathbb P^N$$ which sends a point $$[p_0:\dots : p_n]$$ to $$[M_0(p_0,\dots , p_n):\dots :M_N(p_0,\dots ,p_n)]$$.

Notice that a change in the choice of the order of the monic monomials produces simply the composition of the Veronese map with a change of coordinates. After choosing an order of the variables, e.g., $$x_0<x_1<\dots <x_n$$, a very popular order of the monic monomials is the order in which $$x_0^{d_0}\cdots x_n^{d_n}$$ preceeds $$x_0^{e_0}\cdots x_n^{e_n}$$ if in the smallest index i for which $$d_i\ne e_i$$ we have $$d_i>e_i$$. This order is called lexicographic order , because it reproduces the way in which words are listed in a dictionary. In Sect. 13.​1 we will discuss different types of monomial orderings.

Notice that we can define an analogue of a Veronese map by choosing arbitrary (nonzero) coefficients for the monomials $$M_j$$’s. This is equivalent to choose a weight for the monomials. The resulting map has the same fundamental property of our Veronese map, for which we choose to take all the coefficients equal to 1.

Remark 10.5.2

The Veronese maps are well defined, since for any $$P=[p_0:\dots :p_n]\in \mathbb P^n$$ there exists an index i with $$p_i\ne 0$$, and among the monomials there exists the monomial $$M=x_i^d$$, which satisfies $$M(p_0,\dots ,p_n)=p_i^d\ne 0$$.

The Veronese map is injective. Indeed if $$P=[p_0:\dots : p_n]$$ and $$Q=[q_0:\dots : q_n]$$, have the same image, then the powers of the $$p_i$$’s and the $$q_i$$’s are equal, up to a scalar multiplication. Thus, up to a scalar multiplication, one may assume $$p_i^d=q_i^d$$ for all i, so that $$q_i=e_ip_i$$, for some choice of a d-root of unit $$e_i$$. If the $$e_i$$’s are not all equal to 1, then there exists a monic monomial M such that $$M(e_0,e_1, \dots ,e_n) \ne 1$$, thus $$M(p_0,\dots , p_n)\ne M(q_0,\dots ,q_n)$$, which contradicts $$v_{n,d}(P)=v_{n,d}(Q)$$.

Because of its injectivity, sometimes we will refer to a Veronese map as a Veronese embedding .

The images of Veronese embeddings will be denoted as Veronese varieties .

Example 10.5.3

The Veronese map $$v_{1,3}$$ sends the point $$[x_0:x_1]$$ of $$\mathbb P^1$$ to the point $$[x_0^3:x_0^2x_1:x_0x_1^2:x_1^3]\in \mathbb P^3$$.

The Veronese map $$v_{2,2}$$ sends the point $$[x_0:x_1:x_2]\in \mathbb P^2$$ to the point $$[x_0^2:x_0x_1:x_0x_2:x_1^2:x_1x_2:x_2^2]$$ (notice the lexicographic order).

Proposition 10.5.4

The image of a Veronese map is a projective subvariety of $$\mathbb P^N$$.

Proof

We define equations for $$Y=v_{n,d}(\mathbb P^n)$$.

Consider $$(n+1)$$-tuples of nonnegative integers $$A=(a_0,\dots ,a_n)$$, $$B=(b_0,\dots ,b_n)$$ and $$C=(c_0,\dots ,c_n)$$, with the following property:

(*) $$\sum a_i=\sum b_i =\sum c_i=d$$ and $$a_i+b_i\ge c_i$$ for all i. Define $$D=(d_0,\dots ,d_n)$$, where $$d_i=a_i+b_i-c_i$$, Clearly $$\sum d_i=d$$. For any choice of $$A=(a_0,\dots ,a_n)$$, the monic monomial $$x_0^{a_0}\cdots x_n^{a_n}$$ corresponds to a coordinate in $$\mathbb P^N$$. Call $$M^A$$ the coordinate corresponding to A. Define in the same way $$M^B, M^C$$ and then also $$M^D$$. The polynomial:
$$ f_{ABC} = M^AM^B-M^CM^D $$
is homogeneous of degree 2 and vanishes at the points of Y. Indeed for any $$Q=v_{n,d}([\alpha _0:\dots :\alpha _n])$$ it is easy to see that:
$$ M^AM^B = M^CM^D= \alpha _0^{a_0+b_0}\cdots \alpha _n^{a_n+b_n}, $$
since any $$x_k$$ appears in $$M^CM^D$$ with exponent $$a_k+b_k$$. It follows that Y is contained in the projective subvariety W defined by the forms $$f_{ABC}$$, when A, B, C vary in the set of $$(n+1)$$-tuples with the property (*) above.

To see that $$Y=W$$, take $$Q=[m_0:\dots :m_N]\in W$$. Each $$m_i$$ corresponds to a monic monomial in the $$x_j$$’s, and we assume they are ordered in the lexicographic order.

First, we claim that at least one coordinate $$m_i$$, corresponding to a power $$x_i^d$$, must be nonzero. Indeed, on the contrary, assume that all the coordinates corresponding to powers vanish, and consider a minimal q such that coordinate $$m_q$$ of Q is nonzero. Let $$m_q$$ correspond to the monomial $$x_0^{a_0}\cdots x_n^{a_n}$$. Since $$m_q$$ is not a power, there are at least two indices $$j>i$$ such that $$a_i,a_j>0$$. Put $$A=(a_0,\dots ,a_n)=B$$ and $$C=(c_0,\dots ,c_n)$$ where $$c_i=a_i-1$$, $$c_j=a_j+1$$ and $$c_k=a_k$$ for $$k\ne i,j$$. The $$(n+1)$$-tuples A, B, C satisfy condition (*). One computes that $$D=(d_0,\dots ,d_n)$$ with $$d_i=a_i+1$$, $$d_j=a_j-1$$ and $$d_k=a_k$$ for $$k\ne i,j$$. Moreover, since $$Q\in W$$, then:
$$ M^A(Q)M^B(Q) = M^C(Q)M^D(Q). $$
But we have $$M^A(Q)=M^B(Q)=m_q$$, while $$M^C(Q)=0$$, since $$x_0^{c_0}\cdots x_n^{c_n}$$ preceeds $$x_0^{a_0}\cdots x_n^{a_n}$$ in the lexicographic order. It follows $$m_q^2=0$$, a contradiction.

Then at least one coordinate corresponding to a power is nonzero. Just to fix the ideas, assume that $$m_0$$, which corresponds to $$x_0^d$$ in the lexicographic order, is different from 0. After multiplying the coordinates of Q by $$1/m_0$$, we may assume $$m_0=1$$. Then consider the coordinates corresponding to the monomials $$x_0^{d-1}x_1,\dots x_0^{d-1}x_n$$. In the lexicographic order, they turn out to be $$m_1,\dots , m_n$$, respectively. Put $$P=[1:m_1:\dots :m_n]\in \mathbb P^n$$. We claim that Q is exactly $$v_{n,d}(P)$$.

The claim means that for any coordinate m of Q, corresponding to the monomial $$x_0^{a_0}\cdots x_n^{a_n}$$ we have $$m= m_1^{a_1}\cdots m_n^{a_n}$$. We prove the claim by descending induction on $$a_0$$. The cases $$a_0=d$$ and $$a_0=d-1$$ are clear by construction. Assume that the claim holds when $$a_0>d-s$$ and take m such that $$a_0=d-s$$. In this case there exists some index $$j>0$$ such that $$a_j>0$$. Put $$A=(a_0,\dots ,a_n)$$, $$B=(d,0,\dots ,0)$$ and $$C=(c_0,\dots ,c_n)$$ where $$c_0=a_0+1=d-s+1$$, $$c_j=a_j-1$$, and $$c_k=a_k$$ for $$k\ne 0,j$$. The $$(n+1)$$-tuples A, B, C satisfy condition (*). Thus
$$ M^A(Q)M^B(Q) = M^C(Q)M^D(Q), $$
where $$D=(d_0,\dots ,d_n)$$ and $$d_0=d-1$$, $$d_j=1$$, and $$d_k=0$$ for $$k\ne 0,j$$. It follows by induction that $$M^B(Q)=1$$, $$M^D(Q)=m_j$$ and
$$ M^C(Q)=m_1^{c_1}\cdots m_n^{c_n}=m_1^{a_1}\cdots m_n^{a_n}/m_j. $$
Then $$m=M^A(Q)= M^C(Q)M^D(Q)=m_1^{a_1}\cdots m_n^{a_n}$$, and the claim follows.   $$\square $$

We observe that all the forms $$M^AM^B-M^CM^D$$ are quadratic forms in the variables $$M_i$$’s of $$\mathbb P^N$$. Thus the Veronese varieties are defined in $$\mathbb P^N$$ by quadratic equations.

Example 10.5.5

Consider the Veronese map $$v_{1,3}:\mathbb P^1\rightarrow \mathbb P^3$$. The monic monomials of degree three in 2 variable are (in lexicographic order):
$$ M_0=x_0^3,\quad M_1=x_0^2x_1, \quad M_2=x_0x_1^2,\quad m_3=x_1^3. $$
The equations for the image are obtained by couples A, B, C satisfying condition (*) above. Up to trivialities, these couples are:
$$\begin{aligned}&A=(3,0)\, B=(0,3)\, C=(1,2), \text{ so } D=(2,1) \text{ and } \text{ we } \text{ get }\, M_0M_3-M_1M_2=0, \\&A=(3,0)\, B=(1,2)\, C=(2,1), \text{ so } D=(2,1) \text{ and } \text{ we } \text{ get }\, M_0M_2-M_1^2=0, \\&A=(2,1)\, B=(0,3)\, C=(1,2), \text{ so } D=(1,2) \text{ and } \text{ we } \text{ get }\, M_1M_3-M_2^2=0 \end{aligned}$$
Consider the point $$Q=[3:6:12:24]$$, which satisfies the previous equations. Since the coordinate $$m_0$$ corresponding to $$x_0^3$$ is equal to $$3\ne 0$$, we divide the coordinates of Q by 3 and obtain $$Q=[1:2:4:8]$$. Then $$Q=v_{1,3}([1:2])$$, as one can check directly.

Example 10.5.6

Equations for the image of $$v_{2,2}\subset \mathbb P^5$$ (the classical Veronese surface) are given by:
$$ {\left\{ \begin{array}{ll} M_0M_4 - M_1M_2 &{}=0 \\ M_3M_2 - M_1M_4 &{}= 0 \\ M_5M_1 - M_2M_4 &{}= 0\\ M_3M_5-M_4^2 &{}=0\\ M_0M_5-M_2^2 &{} = 0\\ M_0M_3-M_1^2 &{}=0 \end{array}\right. } $$
The point $$Q=[0:0:0:1:-2:4]$$ satisfies the equations, and indeed it is equal to $$v_{2,2}([0:1:-2]).$$ Notice that in this case, to recover the preimage of Q, one needs to replace $$x_0$$ with $$x_1$$ in the procedure of the proof of Proposition 10.5.4, since the coordinate corresponding to $$x_0^2$$ is 0.

As a consequence of Proposition 10.5.4, one gets the following result.

Theorem 10.5.7

All the Veronese maps are closed in the Zariski topology.

Proof

We need to prove that the image in $$v_{n,d}$$ of a projective subvariety of $$\mathbb P^n$$ is a projective subvariety of $$\mathbb P^N$$.

First notice that if F is a monomial of degree kd in the variables $$x_0,\dots ,x_n$$ of $$\mathbb P^n$$, then it can be written (usually in several ways) as a product of k monomials of degree d in the $$x_i$$’s, which corresponds to a monomial of degree k in the coordinates $$M_0,\dots ,M_N$$ of $$\mathbb P^N$$. Thus, any form f of degree kd in the $$x_j$$’s can be rewritten as a form of degree k in the coordinates $$M_j$$’s.

Take now a projective variety $$X\subset \mathbb P^n$$ and let $$f_1,\dots ,f_s$$ be homogeneous generators for the homogeneous ideal of X. Call $$e_i$$ the degree of $$f_i$$ and let $$k_id$$ be the smallest multiple of d bigger or equal to $$e_i$$. Then consider all the products $$x_j^{k_id-e_i}f_i$$, $$j=0,\dots , n$$. These products are homogeneous forms of degree $$k_id$$ in the $$x_j$$’s. Moreover a point $$P\in \mathbb P^n$$ satisfies all the equations $$x_j^{k_id-e_i}f_i=0$$ if and only if it satisfies $$f_i=0$$, since at least one coordinate $$x_j$$ of P is nonzero.

With the procedure introduced above, transform arbitrarily each form $$x_j^{k_id-e_i}f_i=0$$ in a form $$F_{ij}$$ of degree k in the variables $$M_j$$’s. Then we claim that $$v_{n,d}(X)$$ is the subvariety of $$v_{n,d}(\mathbb P^n)$$ defined by the equations $$F_{ij}=0$$. Since $$v_{n,d}(\mathbb P^n)$$ is closed in $$\mathbb P^N$$, this will complete the proof.

Indeed let Q be a point of $$v_{n,d}(X)$$. The coordinates of Q are obtained by the coordinates of its preimage $$P=[p_0:\dots :p_n]\in X\subset \mathbb P^n$$ by computing in P all the monomials of degree d in the $$x_j$$’s. Thus $$F_{ij}(Q)=0$$ for all i, j if and only if $$x_j^{k_id-e_i}f_i(P)=0$$ for all i, j, i.e., if and only if $$f_i(P)=0$$ for all i. The claim follows.   $$\square $$

Example 10.5.8

Consider the map $$v_{2,2}$$ and let X be the line in $$\mathbb P^2$$ defined by the equation $$f=(x_0+x_1+x_2)=0$$. Since f has degree 1, consider the products:
$$\begin{aligned} x_0f&=x_0^2+x_0x_1+x_0x_2,\\ x_1f&=x_0x_1+x_1^2+x_1x_2,\\ x_2f&=x_0x_2+x_1x_2+x_2^2. \end{aligned}$$
they can be transformed, respectively, in the monomials
$$ M_0+M_1+M_2,\quad M_1+M_3+M_4,\quad M_2+M_4+M_5. $$
Thus the image of X is the variety defined in $$\mathbb P^5$$ by the previous three linear forms and the six quadratic forms of Example 10.5.6, that define $$v_{2,2}(\mathbb P^2)$$.

Next, let us turn to the Segre embeddings.

Definition 10.5.9

Fix $$a_1,\dots ,a_n$$ and $$N=(a_1+1)\cdot (a_2+1) \cdots (a_n+1) -1$$. There are exactly $$N+1$$ monic monomials of multidegree $$(1,\dots ,1)$$ (i.e., multilinear forms) in the variables $$x_{1,0},\dots ,x_{1,a_1}, x_{2,0},\dots , x_{2,a_2},\dots , x_{n,0}\dots x_{n,a_n}$$. Let us choose an order and denote with $$M_0,\dots , M_N$$ these monomials.

The Segre map  of $$a_1,\dots ,a_n$$ is the map $$s_{a_1,\dots ,a_n}: \mathbb P^{a_1}\times \cdots \times \mathbb P^{a_n}\rightarrow \mathbb P^N$$ which sends a point $$P=([p_{10}:\dots : p_{1n_1}], \dots ,[p_{n0}:\dots :p_{na_n}])$$ to $$[M_0(P):\dots :M_N(P)]$$.

The map is well defined, since for any $$i=1,\dots ,n$$ there exists $$p_{ij_i}\ne 0$$, and among the monomials there is $$M=x_{1,j_1}\cdots x_{n,j_n}$$, which satisfies $$M(P)=p_{1j_1}\cdots p_{nj_n}\ne 0$$.

Notice that when $$n=1$$, then the Segre map is the identity.

Proposition 10.5.10

The Segre maps are injective.

Proof

Make induction on n, the case $$n=1$$ being trivial.

For the general case, assume that
$$\begin{aligned} P&=([p_{10}:\dots : p_{1a_1}], \dots ,[p_{n,0}:\dots :p_{n,a_n}]), \\ Q&=([q_{10}:\dots : q_{1a_1}], \dots ,[q_{n,0}:\dots :q_{n,a_n}]) \end{aligned}$$
have the same image. Fix indices such that $$p_{1j_1},\dots ,p_{nj_n}\ne 0$$. The monomial $$M=x_{1,j_1}\cdots x_{n,j_n}$$ does not vanish at P, hence also $$q_{1j_1},\dots ,q_{nj_n}\ne 0$$.
Call $$\alpha =q_{1j_1}/p_{1j_1}$$. Our first task is to show that $$\alpha =q_{1i}/p_{1i}$$ for $$i=1,\dots ,n_1$$, so that $$[p_{11}:\dots : p_{1a_1}]= [q_{11}:\dots : q_{1a_1}]$$. Define $$\beta =(q_{2j_2}\cdots q_{nj_n})/ (p_{2j_1}\cdots p_{nj_n})$$. Then $$\beta \ne 0$$ and:
$$ \alpha \beta =(q_{1j_1}\cdots q_{nj_n})/(p_{1j_1}\cdots p_{nj_n}). $$
Since P, Q have the same image in the Segre map, then for all $$i=1,\dots , a_1$$, the monomials $$M_i=x_{1,i}x_{2,j_2}\cdots x_{n,j_n}$$ satisfy:
$$ \alpha \beta M_i(P)= M_i(Q). $$
It follows immediately $$\alpha \beta (p_{1i}\cdots p_{nj_n}) =(q_{1i}\cdots q_{nj_n})$$ so that $$\alpha \beta p_{1i}=q_{1i}$$ for all i. Thus $$[p_{10}:\dots : p_{1a_1}]=[q_{10}:\dots : q_{1a_1}]$$.

We can repeat the argument for the remaining factors $$[p_{i0}:\dots : p_{ia_i}]=[q_{i0}:\dots : q_{ia_i}]$$ of P, Q ($$i=2,\dots ,n$$), obtaining $$P=Q$$.   $$\square $$

Because of its injectivity, sometimes we will refer to a Segre map as a Segre embedding .

The images of Segre embeddings will be denoted as Segre varieties .

Example 10.5.11

The Segre embedding $$s_{1,1}$$ of $$\mathbb P^1\times \mathbb P^1$$ to $$\mathbb P^3$$ sends the point $$([x_0:x_1],[y_0:y_1])$$ to $$[x_0y_0:x_0y_1:x_1y_0:x_1y_1]$$.

The Segre embedding $$s_{1,2}$$ of $$\mathbb P^1\times \mathbb P^2$$ to $$\mathbb P^5$$ sends the point $$([x_{10}:x_{11}],[x_{20}:x_{21}:x_{22}])$$ to the point:
$$ [x_{10}x_{20}:x_{10}x_{21}:x_{10}x_{22}:x_{11}x_{20}:x_{11}x_{21}:x_{11}x_{22}]. $$
The Segre embedding $$s_{1,1,1}:\mathbb P^1\times \mathbb P^1\times \mathbb P^1\rightarrow \mathbb P^7$$ sends the point $$P=([x_{10}:x_{11}], [x_{20}:x_{21}],[x_{30}:x_{31}])$$ to the point:
$$ [x_{10}x_{20}x_{30}:x_{10}x_{20}x_{31}:x_{10}x_{21}x_{30}:x_{10}x_{21}x_{31}: x_{11}x_{20}x_{30}:x_{11}x_{20}x_{31}:x_{11}x_{21}x_{30}:x_{11}x_{21}x_{31}]. $$

Recall the general notation that with [n] we denote the set $$\{1,\dots ,n\}$$.

Proposition 10.5.12

The image of a Segre map is a projective subvariety of $$\mathbb P^N$$.

Since the set of tensors of rank one corresponds to the image of a Segre map, the proof of the proposition is essentially the same as the proof of Theorem 6.​4.​13. We give the proof here, in the terminology of maps, for the sake of completeness.

Proof

We define equations for $$Y=s_{a_1,\dots ,a_n}(\mathbb P^{a_1}\times \dots \times \mathbb P^{a_n})$$.

For any n-tuple $$A=(\alpha _0,\dots ,\alpha _m)$$ define the form $$M^A$$ of multidegree $$(1,\dots ,1)$$ as follows:
$$ M^A=x_{0\alpha _0}\cdots x_{n\alpha _n}. $$
Then consider any subset $$J\subset [n]$$ and two n-tuples of nonnegative integers $$A=(\alpha _0,\dots ,\alpha _n)$$ and $$B=(\beta _0,\dots ,\beta _n)$$. Define $$C=C_{AB}^J$$ as the n-tuple $$(\gamma _1,\dots ,\gamma _n)$$ such that:
$$ \gamma _i={\left\{ \begin{array}{ll} \alpha _i &{} \text{ if } i\in J, \\ \beta _i &{} \text{ if } i\notin J \end{array}\right. }. $$
Define D as $$D=C_{AB}^{J^c}$$, where $$J^c$$ is the complement of J in [n]. Thus $$D=(\delta _1,\dots ,\delta _n)$$, where:
$$ \delta _i={\left\{ \begin{array}{ll} \beta _i &{} \text{ if } i\in J, \\ \alpha _i &{} \text{ if } i\notin J \end{array}\right. }. $$
Consider the polynomials
$$ f_{AB}^J = M^AM^B-M^CM^D. $$
Every $$f_{AB}^J$$ is homogeneous of degree 2 in the coordinates of $$\mathbb P^N$$. We claim that the projective variety defined by the forms $$f_{AB}^J$$, for all possible choices of A, B, J as above, is exactly equal to Y.
One direction is simple. If:
$$ Q=s_{a_1,\dots ,a_n}([q_{10}:\dots :q_{1a_1}],\dots ,[q_{n0}:\dots :q_{na_n}]) $$
then it is easy to see that both $$M^AM^B(Q)$$ and $$M^CM^D(Q)$$ are equal to the product
$$ q_{1\alpha _1}q_{1\beta _1}q_{2\alpha _2}q_{2\beta _2}\cdots q_{n\alpha _n}q_{n\beta _n}. $$
It follows that Y is contained in the projective subvariety W defined by the forms $$f_{AB}^J$$.

To see the converse, we make induction on the number n of factors. The claim is obvious if $$n=1$$, for in this case the equations $$f^J_{AB}$$ are trivial and the Segre map is the identity on $$\mathbb P^{a_1}$$.

Assume that the claim holds for $$n-1$$ factors. Take $$Q=[m_0:\dots :m_N]\in W$$. Each $$m_i$$ corresponds to a monic monomial $$x_{1i_1}\cdots x_{ni_n}$$ of multidegree $$(1,\dots ,1)$$ in the $$x_{ij}$$’s. Fix a coordinate m of Q different from 0. Just to fix the ideas, we assume that m corresponds to $$x_{10}\cdots x_{n-1\, 0} x_{n0}$$. If m corresponds to another multilinear form, the argument remains valid, it just requires heavier notation.

Consider the point $$Q'$$ obtained from Q by deleting all the coordinates corresponding to multilinear forms in which the last factor is not $$x_{n0}$$. If we consider $$N'=\Pi _2^n (a_i+1)-1$$, then $$Q'$$ can be considered as a point in $$\mathbb P^{N'}$$, moreover the coordinates of $$Q'$$ satisfy all the equation $$f_{A'B'}^{J'}=0$$, where $$A',B'$$ are $$(n-1)$$-tuples $$(\alpha _1,\dots ,\alpha _{n-1}),(\beta _1,\dots ,\beta _{n-1})$$ and $$J'\subset [n-1]$$. It follows by induction that $$Q'$$ corresponds to the image of some $$P'\in \mathbb P^{a_1}\times \dots \times \mathbb P^{a_{n-1}}$$ in the Segre embedding in $$\mathbb P^{N'}$$.

Write $$P'=([p_{10}:\dots :p_{1a_1}],\dots ,[p_{n-1\, 0}:\dots :p_{n-1\, a_{n-1}}])$$. Since $$m\ne 0$$, i.e., the coordinate of $$Q'$$ corresponding to m is nonzero, then we must have $$p_{j0}\ne 0$$ for all $$j=1,\dots n$$. Let $$m_i$$, $$i=1,\dots ,a_n$$, be the coordinate of Q corresponding to the multilinear form $$x_{10}\cdots x_{ni_n}$$. Then we prove that the coordinate $$m'$$ corresponding to $$x_{1i_1}\cdots x_{ni_n}$$ satisfies
$$ m'= \frac{m_{i_n}}{m} p_{1i_1}\cdots p_{n-1\, i_{n-1}}, $$
This will prove that Q is the image of the point:
$$ P=([p_{10}:\dots :p_{1a_1}],\dots ,[p_{n-1\, 0}:\dots :p_{n-1\, a_{n-1}}], [p_{n0}:\dots :p_{na_n}]), $$
where $$p_{ni}=m_i/m$$ for all $$i=0,\dots , a_n$$.

To prove the claim, take $$A=(i_1,\dots ,i_n)$$, $$B=(0,\dots ,0)$$ and $$J=\{n\}$$. Then we have $$\gamma _k=\alpha _k$$ and $$\delta _k=0$$ for $$k=1,\dots , n-1$$, while $$\gamma _n=0$$ and $$\delta _n=i_n$$. Thus $$M^A(Q)=m'$$, $$M^B(Q)=m$$, $$M^D(Q)=m_{i_n}$$ and, by induction $$M^C(Q)=p_{1i_1}\cdots p_{n-1\, i_{n-1}}$$. Since $$M^A(Q)M^B(Q)=M^C(Q)M^D(Q)$$, the claim follows.   $$\square $$

We observe that all the forms $$M^AM^B-M^CM^D$$ are quadratic forms in the variables $$M_i$$’s of $$\mathbb P^N$$. Thus the Segre varieties are defined in $$\mathbb P^N$$ by quadratic equations.

Example 10.5.13

Consider the Segre embedding $$s_{1,1}:\mathbb P^1\times \mathbb P^1\rightarrow \mathbb P^3$$. The 4 variables $$M_0,M_1,M_2,M_3$$ in $$\mathbb P^3$$ correspond, respectively, to the multilinear forms
$$ M_0=x_{10}x_{20},\, M_1=x_{10}x_{21},\, M_2=x_{11}x_{20},\, M_3=x_{11}x_{21}. $$
If we take $$A=(0,0), B=(1,1)$$ and $$J=\{1\}$$, we get that $$C=(0,1), D=(1,0)$$. Thus $$M^A$$ corresponds to $$x_{10}x_{20}=M_0$$, $$M^B$$ corresponds to $$x_{11}x_{21}=M_3$$, $$M^C$$ corresponds to $$x_{10}x_{21}=M_1$$ and $$M^D$$ corresponds to $$x_{11}x_{20}=M_2$$. We get thus the equation:
$$ M_0M_3-M_1M_2=0. $$
The other choices for A, B, J yield either trivialities or the same equation.

Hence the image of $$s_{1,1}$$ is the variety defined in $$\mathbb P^3$$ by the equation $$M_0M_3-M_1M_2=0$$. It is a quadric surface (see Fig. 10.1).

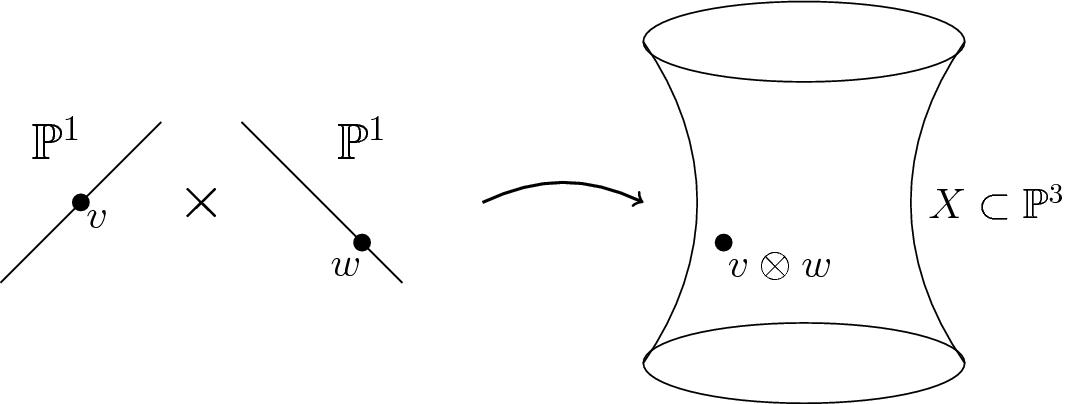
../images/485183_1_En_10_Chapter/485183_1_En_10_Fig1_HTML.png
Fig. 10.1

Segre embedding of $$\mathbb P^1\times \mathbb P^1$$ in $$\mathbb P^3$$

Example 10.5.14

Equations for the image of $$s_{1,2}\subset \mathbb P^5$$ (up to trivialities) are given by:
$$ {\left\{ \begin{array}{ll} M_0M_4 - M_1M_3 &{}=0 \text{ for } A=(0,0),\, B=(1,1),\, J=\{1\}\\ M_0M_5 - M_2M_3 &{}= 0 \text{ for } A=(0,0),\, B=(1,2),\, J=\{1\}\\ M_5M_1 - M_2M_4 &{}= 0 \text{ for } A=(0,1),\, B=(1,2),\, J=\{1\}, \end{array}\right. } $$
where $$M_0=x_{10}x_{20}$$, $$M_1=x_{10}x_{21}$$, $$M_2=x_{10}x_{22}$$, $$M_3=x_{11}x_{20}$$, $$M_4=x_{11}x_{21}$$, $$M_5=x_{11}x_{22}$$.

Example 10.5.15

We can give a more direct representation of the equations defining the Segre embedding of the product of two projective spaces $$\mathbb P^{a_1}\times \mathbb P^{a_2}$$.

Namely, we can plot the coordinates of $$Q\in P^N$$ in a $$(a_1+1)\times (a_2+1)$$ matrix, putting in the entry ij the coordinate corresponding to $$x_{1\, i-1}x_{2\, j-1}$$.

Conversely, any matrix $$(a_1+1)\times (a_2+1)$$ (except for the null matrix) corresponds uniquely to a set of coordinates for a point $$Q\in \mathbb P^N$$. Thus we can identify $$\mathbb P^N$$ with the projective space over the linear space of matrices of type $$(a_1+1)\times (a_2+1)$$ over $$\mathbb C$$.

In this identification, the choice of $$A=(i,j), B=(k,l)$$ and $$J=\{1\}$$ (choosing $$J=\{2\}$$ we get the same equation, up to the sign) produces a form equivalent to the $$2\times 2$$ minor:
$$ m_{ij}m_{kl}-m_{il}m_{kj} $$
of the matrix.

Thus, the image of a Segre embedding of two projective space can be identified with the set of matrices of rank 1 (up to scalar multiplication) in a projective space of matrices.

As a consequence of Proposition 10.5.12, one gets the following result.

Theorem 10.5.16

All the Segre maps are closed in the Zariski topology.

Proof

We need to prove that the image in $$s_{a_1,\dots ,a_n}$$ of a multiprojective subvariety X of $$V=\mathbb P^{a_1}\times \dots \times \mathbb P^{a_n}$$ is a projective subvariety of $$\mathbb P^N$$.

First notice that if F is a monomial of multidegree $$(d,\dots ,d)$$ in the variables $$x_{ij}$$ of V, then it can be written (usually in several ways) as a product of k multilinear forms in the $$x_{ij}$$’s, which corresponds to a monomial of degree d in the coordinates $$M_0,\dots ,M_N$$ of $$\mathbb P^N$$. Thus, any form f of multidegree $$(d,\dots ,d)$$ in the $$x_{ij}$$’s can be rewritten as a form of degree d in the coordinates $$M_j$$’s.

Take now a projective variety $$X\subset V$$ and let $$f_1,\dots ,f_s$$ be multihomogeneous generators for the ideal of X. Call $$(d_{k1},\dots ,d_{kn})$$ the multidegree of $$f_k$$ and let $$d_k=\max \{d_{k1}, \dots ,d_{kn}\}$$. Consider all the products $$x_{1j_1}^{d_k-d_{k1}}\cdots x_{nj_n}^{d_k-d_{kn}}f_k$$. These products are multihomogeneous forms of multidegree $$(d_k,\dots ,d_k)$$ in the $$x_{ij}$$’s. Moreover a point $$P\in V$$ satisfies all the equations $$x_{1j_1}^{d_k-d_{k1}}\cdots x_{nj_n}^{d_k-d_{kn}}f_k=0$$ if and only if it satisfies $$f_k=0$$, since for all i at least one coordinate $$x_{ij}$$ of P is nonzero.

With the procedure introduced above, transform arbitrarily each form $$x_{1j_1}^{d_k-d_{k1}}\cdots x_{nj_n}^{d_k-d_{kn}}f_k$$ in a form $$F_{kj_1,\dots ,j_n}$$ of multidegree $$(d_k,\dots ,d_k)$$ in the variables of $$\mathbb P^N$$. Then we claim the $$s_{a_1,\dots ,a_n}(X)$$ is the subvariety of $$s_{a_1,\dots ,a_n}(V)$$ defined by the equations $$F_{kj_1,\dots ,j_n}=0$$. Since $$s_{a_1,\dots ,a_n}(V)$$ is closed in $$\mathbb P^N$$, this will complete the proof.

To prove the claim, let Q be a point of $$s_{a_1,\dots ,a_n}(X)$$. The coordinates of Q are obtained by the coordinates of its preimage $$P=([p_{10}:\dots :p_{1n_1}],\dots ,[p_{n0}:\dots :p_{na_n}]\in X\subset V$$ by computing all the multilinear forms in the $$x_{ij}$$’s at P. Thus $$F_{kj_1,\dots ,j_n}(Q)=0$$ for all $$k,j_1,\dots ,j_n$$ if and only if $$f_k(P)=0$$ for all k. The claim follows.   $$\square $$

Example 10.5.17

Consider the variety X in $$\mathbb P^1\times \mathbb P^1$$ defined by the multihomogeneous form $$f_1=x_{10}x^2_{21}+x_{11}x_{20}^2$$ of multidegree (1, 2). Then we have:
$$\begin{aligned}&x_{10}f= x_{10}^2x^2_{21}+x_{10}x_{11}x_{20}^2=(x_{10}x_{21})^2+(x_{10}x_{21}\, x_{01}x_{21})= M_1^2+M_1M_3, \\&x_{11}f= x_{11}x_{10}x^2_{21}+x_{11}^2x_{20}^2=(x_{10}x_{21}\, x_{11}x_{21})+( x_{11}x_{21})^2= M_1M_3+M_3^2. \end{aligned}$$
These two forms, together with the form $$M_0M_3-M_1M_2$$ that defines $$s_{1,1}(\mathbb P^1\times \mathbb P^1)$$ in $$\mathbb P^3$$, define the image of X in the Segre embedding.

Remark 10.5.18

Even if we take a minimal set of forms $$f_k$$’s that define $$X\subset \mathbb P^{a_1}\times \dots \times \mathbb P^{a_n}$$, with the procedure of Theorem 10.5.16 we do not find, in general, a minimal set of forms that define $$s_{a_1,\dots ,a_n}(X)$$.

Indeed the ideal generated by the forms $$F_{kj_1,\dots ,j_n}$$ constructed in the proof of Theorem 10.5.16 needs not, in general, to be radical or even saturated.

We end this section by pointing out a relation between the Segre and the Veronese embeddings of projective and multiprojective spaces.

Definition 10.5.19

A multiprojective space $$\mathbb P^{a_1}\times \dots \times \mathbb P^{a_n}$$ is cubic  if $$a_i=a$$ for all i.

We can embed $$\mathbb P^a$$ into the cubic multiprojective space $$\mathbb P^a\times \dots \times \mathbb P^a$$ (n times) by sending each point P to $$(P,\dots ,P)$$. We will refer to this map as the diagonal embedding. It is easy to see that the diagonal embedding is an injective multiprojective map.

Example 10.5.20

Consider the cubic product $$\mathbb P^1\times \mathbb P^1$$ and the diagonal embedding $$\delta :\mathbb P^1\rightarrow \mathbb P^1\times \mathbb P^1$$.

The point $$P=[p_0:p_1]$$ of $$\mathbb P^1$$ is mapped to $$([p_0:p_1],[p_0:p_1])\in \mathbb P^1\times \mathbb P^1$$. Thus the Segre embedding of $$\mathbb P^1\times \mathbb P^1$$, composed with $$\delta $$, sends P to the point $$[p_0^2:p_0p_1:p_1p_0:p_1^2]\in \mathbb P^3$$.

We see that the coordinates of the image have a repetition: the second and the third coordinates are equal, due to the commutativity of the product of complex numbers. In other words the image $$s_{1,1}\circ \delta (\mathbb P^1)$$ satisfies the linear equation $$M_1-M_2=0$$ in $$\mathbb P^3$$.

We can get rid of the repetition if we project $$\mathbb P^3\rightarrow \mathbb P^2$$ by forgetting the third coordinate, i.e., by taking the map $$\mathbb C^4\rightarrow \mathbb C^3$$ that maps $$(M_0,M_1,M_2,M_3)$$ to $$(M_0,M_1,M_3)$$. The projective kernel of this map is the point [0 : 0 : 1 : 0], which does not belong to $$\delta (\mathbb P^1)$$, since $$P=[p_0:p_1]\in \mathbb P^1$$ cannot have $$p_0^2=p_1^2=0$$. Thus we obtain a well defined projection $$\pi :s_{1,1}\circ \delta (\mathbb P^1)\rightarrow \mathbb P^2$$.

The composition $$\pi \circ s_{1,1}\circ \delta :\mathbb P^1\rightarrow \mathbb P^2$$ corresponds to the map which sends $$[p_0:p_1]$$ to $$[p_0^2:p_0p_1:p_1^2]$$. In other words $$\pi \circ s_{1,1}\circ \delta $$ is the Veronese embedding $$v_{1,2}$$ of $$\mathbb P^1$$ in $$\mathbb P^2$$.

The previous example generalizes to any cubic Segre product.

Theorem 10.5.21

Consider a cubic multiprojective space $$\mathbb P^n\times \dots \times \mathbb P^n$$, with $$r>1$$ factors. Then the Veronese embedding $$v_{n,r}$$ of degree r corresponds to the composition of the diagonal embedding $$\delta $$, the Segre embedding $$s_{n,\dots ,n}$$ and one projection.

Proof

For any $$P=[p_0:\dots :p_n]\in \mathbb P^n$$ the point $$s_{n,\dots ,n}\circ \delta (P)$$ has repeated coordinates. Indeed for any permutation $$\sigma $$ on [r] the coordinate corresponding to $$x_{1i_1}\cdots x_{ri_r}$$ of $$s_{n,\dots ,n}\circ \delta (P)$$ is equal to $$p_{i_1}\cdots p_{i_r}$$, hence its equal to the coordinate corresponding to $$x_{1i_{\sigma (1)}}\cdots x_{ri_{\sigma (r)}}$$. To get rid of these repetition, we can consider coordinates corresponding to multilinear forms $$x_{1i_1}\cdots x_{ri_r}$$ that satisfy:

(**) $$\qquad i_1\le i_2\le \dots \le i_r$$.

By easy combinatorial computations, the number of these forms is equal to $$\left( {\begin{array}{c}n+d\\ d\end{array}}\right) $$. Forgetting the variables corresponding to multilinear forms that do not satisfy condition (**) is equivalent to take a projection $$\phi :C^{N+1}\rightarrow \mathbb C^{N'+1}$$, where $$N'+1=\left( {\begin{array}{c}n+d\\ d\end{array}}\right) $$. The kernel of this projections is the set of $$(N+1)$$-tuples in which the coordinates corresponding to linear forms that satisfy (**) are all zero. Among these coordinates there are those for which $$i_1=i_2=\dots =i_r=i$$, $$i=0,\dots , n$$. So $$s_{n,\dots ,n}\circ \delta (P)$$ cannot meet the projective kernel of $$\phi $$, because that would imply $$p_0^d=\dots =p_n^d=0$$.

Thus $$\phi \circ s_{n,\dots ,n}\circ \delta (P)$$ is well defined for all $$P\in \mathbb P^n$$. The coordinate of $$s_{n,\dots ,n}\circ \delta (P)$$ corresponding to $$x_{1i_1}\cdots x_{ri_r}$$ is equal to $$p_0^{d_0}\cdots p_n^{d_n}$$, where, for $$i=0,\dots ,n,d_i$$ $$d_i$$, is the number in which i appears among $$i_1,\dots ,i_r$$. Then $$d_0+\dots +d_n=r$$.

It is clear then that computing $$\phi \circ s_{n,\dots ,n}\circ \delta (P)$$ corresponds to computing (once) in P all the monomials of degree r in $$x_0,\dots ,x_n$$.   $$\square $$

10.6 The Chow’s Theorem

We prove in this section the Chow’s theorem: every projective or multiprojective map is closed in the Zariski topology.

Proposition 10.6.1

Every projective map $$f:\mathbb P^n\rightarrow \mathbb P^m$$ factors through a Veronese map, a change of coordinates and a projection.

Proof

By Proposition 9.​3.​2, there are homogeneous polynomials $$f_0,\dots , f_m \in \mathbb C[x_0,\dots , x_n]$$ of the same degree d, which do not vanish simultaneously at any point $$P\in \mathbb P^n$$, and such that f is defined by the $$f_j$$’s. Each $$f_j$$ is a linear combination of monic monomials of degree d. Hence, there exists a change of coordinates g in the target space $$\mathbb P^N$$ of $$v_{n,d}$$ such that f is equal to $$v_{n,d}$$ followed by g and by the projection to the first $$m+1$$ coordinates. Notice that since $$(f_0(P),\dots , f_m(P))\ne 0$$ for all $$P\in \mathbb P^n$$, then the projection is well defined on the image of $$g\circ v_{n,d}$$.   $$\square $$

A similar procedure holds to describe a canonical decomposition of multiprojective maps.

Proposition 10.6.2

Every multiprojective map $$f:\mathbb P^{a_1}\times \cdots \times \mathbb P^{a_n}\rightarrow \mathbb P^N$$ factors through Veronese maps, a Segre map, a change of coordinates and a projection.

Proof

By Proposition 9.​3.​11, there are multihomogeneous polynomials $$f_1,\dots , f_{s}$$ in the ring $$\mathbb C[x_{1,0},\dots ,x_{1,a_1}, \dots , x_{n,0}\dots x_{n,a_n}]$$ of the same multidegrees $$(d_1,\dots ,d_n)$$, which do not vanish simultaneously at any point $$P\in \mathbb P^{a_1}\times \cdots \times \mathbb P^{a_n}$$, and such that f is defined by the $$f_j$$’s. Each $$f_j$$ is a linear combination of products of monic monomials, of degrees $$d_1,\dots ,d_n$$, in the set of coordinates $$(x_{1,0},\dots ,x_{1,a_1}),\dots , (x_{n,0}\dots x_{n,a_n})$$, respectively. If $$v_{a_i,d_i}$$ denotes the Veronese embedding of degree $$d_i$$ of $$\mathbb P^{a_i}$$ into the corresponding space $$\mathbb P^{N_i}$$, then f factors through $$v_{a_1,d_1}\times \cdots \times v_{a_n,d_n}$$ followed by a multilinear map $$F:\mathbb P^{a_1}\times \cdots \times \mathbb P^{a_n}\rightarrow \mathbb P^N$$, which in turn is defined by multihomogeneous polynomials $$F_1,\dots , F_s$$ of multidegree $$(1,\dots ,1)$$ (multilinear forms). Each $$F_j$$ is a linear combination of products of n coordinates in the sets $$(x_{1,0},\dots ,x_{1,a_1}),\dots , (x_{n,0}\dots x_{n,a_n})$$, respectively. Hence F factors through a Segre map $$s_{N_1,\dots ,N_r}$$, followed by a change of coordinates in $$\mathbb P^M$$, $$M=(N_1+1)\cdots (N_r+1)-1$$ which sends the linear polynomial associated to the $$F_j$$’s to the first $$N+1$$ coordinates of $$\mathbb P^N$$, and then followed by a projection to the first s coordinates.   $$\square $$

Now we are ready to state and prove the Chow’s Theorem.

Theorem 10.6.3

(Chow’s Theorem) Every projective map $$f:\mathbb P^n\rightarrow \mathbb P^N$$ is Zariski closed, i.e., the image of a projective subvariety is a projective subvariety.

Every multiprojective map $$f:\mathbb P^{a_1}\times \cdots \times \mathbb P^{a_n}\rightarrow \mathbb P^M$$ is Zariski closed.

Proof

In view of the two previous propositions, this is just an obvious consequence of Theorems 10.5.7 and 10.5.16.   $$\square $$

We will see, indeed, in Corollary 11.​3.​7, that the conclusion of Chow’s Theorem holds for any projective map $$f:X\rightarrow Y$$ between any projective varieties.

Example 10.6.4

Let us consider the projective map $$f:\mathbb P^1\rightarrow \mathbb P^2$$ defined by
$$ f(x_1,x_2) = (x_1^3, x_1^2x_2-x_1x_2^2, x_2^3). $$
We can decompose f as the Veronese map $$v_{1,3}$$, followed by the linear isomorphism $$g(a,b,c)=(a,b-c, c-d,d)$$ and then followed by the projection $$\pi $$ to the first, second and fourth coordinate.
Namely:
$$\begin{aligned}&(\pi \circ g \circ v_{1,3})(x_1,x_2) = (\pi \circ g)(x_1^3,x_1^2x_2,x_1x_2^2,x_2^3) =\\&\qquad \qquad \quad = \pi (x_1^3, x_1^2x_2-x_1x_2^2, x_1x_2^2-x_2^3, x_2^3) = (x_1^3, x_1^2x_2-x_1x_2^2, x_2^3). \end{aligned}$$
The image of $$\pi $$ is a projective curve in $$\mathbb P^3$$, whose equation can be obtained by elimination theory. One can see that, in the coordinates $$z_0,z_1,z_2$$ of $$\mathbb P^2$$, $$f(\mathbb P^1)$$ is the zero locus of
$$ z_1^3-z_0z_2(z_0-3z_1-z_2). $$

Example 10.6.5

Let us consider the subvariety Y of $$\mathbb P^1\times \mathbb P^1$$, defined by the multihomogeneous polynomial $$f= x_0-x_1$$, of multidegree (1, 0) in the coordinates $$(x_0,x_1),(y_0,y_1)$$ of $$\mathbb P^1\times \mathbb P^1$$. Y corresponds to $$[1:1]\times \mathbb P^1$$.

Take the Segre embedding $$s:\mathbb P^1\times \mathbb P^1\rightarrow \mathbb P^3$$,
$$ (x_0,x_1),(y_0,y_1) = (x_0y_0,x_0y_1,x_1y_0,x_1y_1). $$
Then the image $$s(\mathbb P^1\times \mathbb P^1)$$ corresponds to the quadric Q in $$\mathbb P^3$$ defined by the vanishing of the homogeneous polynomial $$g=z_0z_3-z_1z_2$$.

The image of Y is a projective subvariety of $$\mathbb P^3$$, which is contained in Q, but it is no longer defined by g and another polynomial: we need two polynomials, other than g.

Namely, Y is defined also by the two multihomogeneous polynomials, of multidegree (1, 1), $$f_0=fy_0=x_0y_0-x_1y_0$$ and $$f_1=fy_1=x_0y_1-x_1y_1$$. Thus s(Y) is defined in $$\mathbb P^3$$ by $$g, g_0=z_0-z_1, g_1=z_2-z_3$$. (Indeed, in this case, $$g_0,g_1$$ alone are sufficient to determine s(Y), which is a line).

Other examples and applications are contained in the exercise section.

10.7 Exercises

Exercise 31

Recall that a map between topological spaces is closed if it sends closed sets to closed sets.

Prove that the composition of closed maps is a closed map, the product of closed maps is a closed map, and the restriction of a closed map to a closed set is itself a closed map.

Exercise 32

Given a linear surjective map $$\phi :\mathbb C^{m+1}\rightarrow \mathbb C^{n+1}$$ and a subvariety $$X\subset \mathbb P^m$$ which does not meet $$K_\phi $$, find the polynomials that define the projection of X from $$K_\phi $$, in terms of the matrix associated to $$\phi $$.

Exercise 33

Let f, g be nonzero polynomials in $$\mathbb C[x]$$, with f constant. Prove that the resultant R(f, g) is nonzero.

Exercise 34

Consider the Veronese map $$\mathbb P^1\rightarrow \mathbb P^3$$ defined in Example 10.5.17 and call X the image. Show that the three equations for X found in Example 10.5.17 are nonredundant: for any choice of two of them, there exists a point Q which satisfies the two equations but does not belong to X.