© Springer Nature Switzerland AG 2019
C. Bocci, L. ChiantiniAn Introduction to Algebraic Statistics with TensorsUNITEXT118https://doi.org/10.1007/978-3-030-24624-2_7

7. Symmetric Tensors

Cristiano Bocci1   and Luca Chiantini1
(1)
Dipartimento di Ingegneria dell’Informazione e Scienze Matematiche, Università di Siena, Siena, Italy
 
 
Cristiano Bocci
Email: cristiano.bocci@unisi.it

In this chapter, we make a specific analysis of the behavior of symmetric tensors, with respect to the rank and the decomposition.

We will see, indeed, that besides their utility to understand some models of random systems, symmetric tensors have a relevant role in the study of the algebra and the computational complexity of polynomials.

7.1 Generalities and Examples

Definition 7.1.1

A cubic  tensor is a tensor of type $$a_1\times \dots \times a_n $$ where all the $$a_i$$’s are equal, i.e., a tensor of type $$d\times \dots \times d$$ (n times).

We say that a cubic tensor T is symmetric  if for any multi-index $$(i_1,\dots ,i_n)$$ and for any permutation $$\sigma $$ on the set $$\{i_1,\dots ,i_n\}$$, it satisfies
$$ T_{i_1,\dots ,i_n} = T_{i_{\sigma (1)},\dots ,i_{\sigma (n)}}.$$

Example 7.1.2

When T is a square matrix, then the condition for the symmetry of T simply requires that $$T_{i,j} = T_{j,i}$$ for any choice of the indices. In other words, our definition of symmetric tensor coincides with the plain old definition of symmetric matrix, when T has dimension 2.

If T is a cubic tensor of type $$2\times 2 \times 2$$, then T is symmetric if and only if the following equalities hold:
$$ {\left\{ \begin{array}{ll} T_{1,1,2} &{}= T_{1,2,1} = T_{2,1,1} \\ T_{2,2,1} &{}= T_{2,1,2} = T_{1,2,2} \end{array}\right. } $$
An example of a $$2\times 2 \times 2$$ symmetric tensor is the following:
../images/485183_1_En_7_Chapter/485183_1_En_7_Figa_HTML.png

Remark 7.1.3

The set of symmetric tensors is a linear subspace of $$K^{d,\dots ,d}$$. Namely, it is defined by a set of linear equations:
$$ T_{i_1,\dots ,i_n} = T_{\sigma (i_1), \dots , \sigma (i_n)}$$
in the coordinates of $$K^{d,\dots ,d}$$.

As a vector space itself, the space of symmetric tensors of type $$d\times \cdots \times d$$, n times, is usually denoted by $$Sym^n(K^d)$$.

Of course, from the point of view of multi-linear forms, $$Sym^n(K^d)$$ coincides with the space of symmetric multi-linear maps $$(K^d)^n\rightarrow K$$.

As we will see later (see Proposition 7.3.8), the dimension of $$Sym^n(K^d)$$ is
$$ \dim (Sym^n(K^d)) =\left( {\begin{array}{c}n+d-1\\ n\end{array}}\right) = \left( {\begin{array}{c}n+d-1\\ d-1\end{array}}\right) .$$

7.2 The Rank of a Symmetric Tensor

Next step is the study of the behavior of symmetric tensors with respect to the rank. It is easy to realize that there are symmetric tensors of rank 1, i.e., the space $$Sym^n(K^d)$$ intersects the set of decomposable tensors. Just to give an instance, look at:

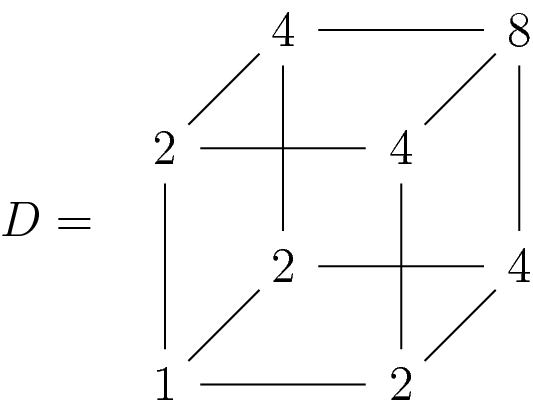
../images/485183_1_En_7_Chapter/485183_1_En_7_Figb_HTML.png

The following proposition determines how one construct decomposable, symmetric tensors.

Proposition 7.2.1

Let T be a cubic tensor of type $$d\times \cdots \times d$$, n times. Then T is symmetric, of rank 1, if and only if there exist a nonzero scalar $$\lambda \in K$$ and a nonzero vector $$v\in K^d$$ with:
$$ T = \lambda (v\otimes v \otimes \cdots \otimes v).$$
If moreover K is an algebraically closed field (as the complex field $$\mathbb C$$), then we may assume $$\lambda =1$$.

Proof

If $$T = \lambda (v\otimes v \otimes \cdots \otimes v)$$, $$v\ne 0$$, then T cannot be zero by Proposition 6.​2.​8, thus it has rank 1. Moreover if $$v=(\alpha _1,\dots ,\alpha _d)$$, then for any multi-index $$(i_1,\dots ,i_n)$$ and for any permutation $$\sigma $$:
$$ T_{i_1,\dots ,i_n} =\alpha _{i_1}\cdots \alpha _{i_n} = T_{\sigma (i_1),\dots ,\sigma (i_n)}$$
thus T is symmetric.
Conversely, assume that T is symmetric of rank 1, say $$T=v_1\otimes \cdots \otimes v_n$$, where no $$v_i\in K^d$$ can be 0, by Proposition 6.​2.​8. Write $$v_i=(v_{i,1},\dots , v_{i,d})$$ and fix a multi-index $$(i_1,\dots ,i_n)$$ such that $$v_{1,i_1}\ne 0$$, ..., $$v_{n,i_n}\ne 0$$. Then $$T_{i_1,\dots ,i_n}= v_{1,i_1}\cdots v_{n,i_n}$$ cannot vanish. Define $$b_2 = v_{2,i_1}/v_{1,i_1}$$. Then we claim that $$v_2=b_2v_1$$. Namely, for all j we have, by symmetry:
$$ v_{1,i_1}v_{2,j} v_{3,i_3}\cdots v_{n,i_n} = T_{i_1,j,i_3,\dots ,i_n} = T_{j,i_1,i_3,\dots ,i_n} = v_{1,j}v_{2,i_1} v_{3,i_3}\cdots v_{n,i_n}, $$
which means that $$ v_{1,i_1}v_{2,j}= v_{1,j}v_{2,i_1}$$, so that $$v_{2,j}=b_2v_{1,j}$$. Similarly we can define $$b_3 = v_{3,i_1}/v_{1,i_1}$$,..., $$b_d = v_{d,i_1}/v_{1,i_1}$$, and obtain that $$v_3=b_3v_1$$, ..., $$v_d=b_dv_1$$. Thus, if $$\lambda =b_2\cdot b_3 \cdot \cdots \cdot b_d$$, then
$$ T= v_1\otimes v_2\otimes \cdots \otimes v_n= v_1\otimes (b_2v_1)\otimes \cdots \otimes (b_nv_1)=\alpha (v_1\otimes v_1 \otimes \cdots \otimes v_1). $$
When K is algebraically close, then take a dth root $$\beta $$ of $$\lambda \in K$$ and define $$v=\beta v_1$$. Then $$T=\beta ^d(v_1\otimes v_1\otimes \cdots \otimes v_1)= v\otimes v\otimes \cdots \otimes v$$.$$\square $$

Notice that purely algebraic properties of K can be relevant in determining the shape of a decomposition of a tensor.

Remark 7.2.2

In the sequel, we will often write $$v^{\otimes d}$$ for $$v\otimes v\otimes \cdots \otimes v$$, d times.

If K is algebraically closed, then a symmetric tensor $$T\in Sym^n(K^d)$$ of rank 1 has a finite number (exactly: d) decompositions as a product $$T= v^{\otimes d}$$.

Namely if $$w\otimes \cdots \otimes w= v\otimes \cdots \otimes v$$, then by Proposition 6.​2.​9 there exists a scalar $$\beta $$ such that $$w=\beta v$$ and moreover $$\beta ^d=1$$, thus w is equal to v multiplied by a dth root of unity.

Passing from rank 1 to higher ranks, the situation becomes suddenly more involved.

The definition itself of rank of a symmetric tensors is not completely trivial, as we have two natural choices for it:
  • First choice. The rank of a symmetric tensor $$T\in Sym^n(K^d)$$ is simply its rank as a tensor in $$K^{d,\dots ,d}$$, i.e., it is the minimum r for which one has r decomposable tensors $$T_1$$,...,$$T_r$$ with
    $$ T = T_1+\cdots +T_r.$$
  • Second choice. The rank of a symmetric tensor $$T\in Sym^n(K^d)$$ is the minimum r for which one has r symmetric decomposable tensors $$T_1$$,...,$$T_r$$ with
    $$ T = T_1+\cdots +T_r. $$

Then, the natural question is about which choice gives the correct definition. Here, correct definition means the definition which proves to be most useful, for the applications to Multi-linear Algebra and random systems.

The reader could be disappointed in knowing that there is no clear preference between the two options: each can be preferable, depending on the point of view.

Thus, we will leave the word rank for the minimum r for which one has a decomposition $$ T = T_1+\cdots +T_r$$, with the $$T_i$$’s not necessarily symmetric (i.e., the first choice above).

Then, we give the following:

Definition 7.2.3

The symmetric rank  $$\mathrm{srank}(T)$$ of a symmetric tensor $$T\in Sym^n(K^d)$$ is the minimum r for which one has r symmetric decomposable tensors $$T_1$$,...,$$T_r$$ with
$$ T = T_1+\cdots +T_r.$$
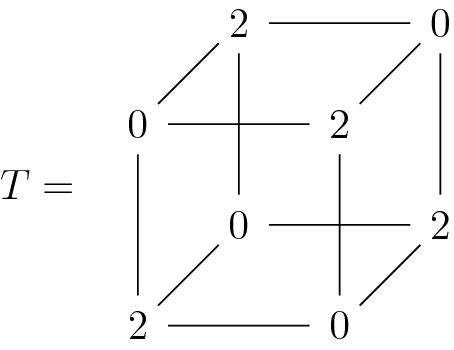
../images/485183_1_En_7_Chapter/485183_1_En_7_Figc_HTML.png

Example 7.2.4

The symmetric tensor

has not rank 1, as one can compute by taking the determinant of some face.

T has rank 2, because it is expressible as the sum of two decomposable tensors $$T=T_1+T_2$$, where

and $$T_1=(1,1)^{\otimes 3}$$, $$T_2= (-1,1)^{\otimes 3}$$.

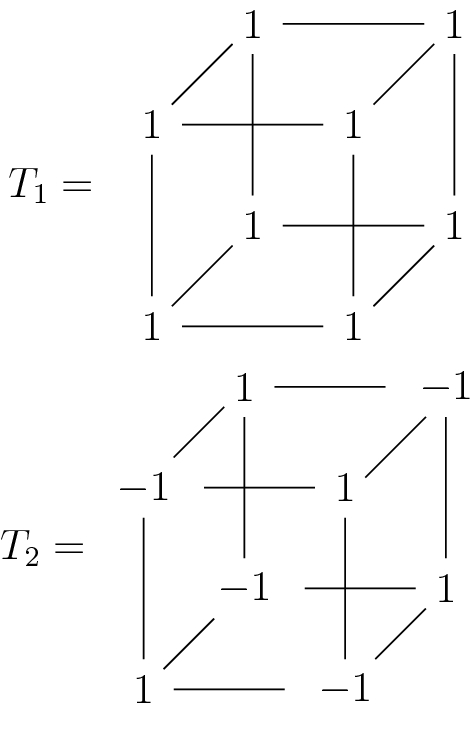
../images/485183_1_En_7_Chapter/485183_1_En_7_Figd_HTML.png
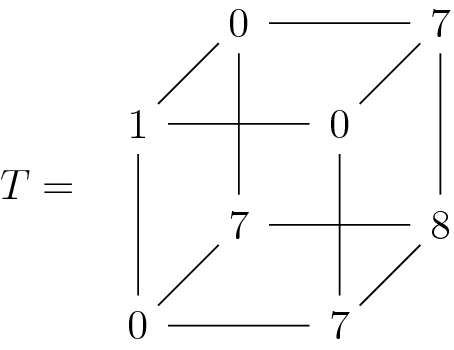
../images/485183_1_En_7_Chapter/485183_1_En_7_Fige_HTML.png

Example 7.2.5

The tensor (over $$\mathbb C$$):

is not decomposable. Let us prove that the symmetric rank is bigger than 2.

Assume that $$T = (a,b)^{\otimes 3} + (c,d)^{\otimes 3}$$. Then we have
$$ {\left\{ \begin{array}{ll} a^3c^3 &{}= 1 \\ a^2b + c^2 d &{}= 0 \\ ab^2+cd^2 &{}= 7 \\ b^3d^3 &{}=8. \end{array}\right. } $$
Notices that none of a, b, c, d can be 0. Moreover we have $$ac=\epsilon $$ and $$bd=2\epsilon '$$, where $$\epsilon ,\epsilon '$$ are two cubic roots of unit, not necessarily equal. But then $$c= \epsilon /a$$ and $$d=\epsilon '/b$$, so that $$a^2b+c^2d=0$$ yields $$1+\epsilon ^2\epsilon '=0$$, which cannot hold, because $$-1$$ is not a cubic root of unit.

Remark 7.2.6

Proposition 7.2.1 shows in particular that any symmetric tensor of (general) rank 1 has also the symmetric rank equal to 1.

The relations between the rank and the symmetric rank of a tensor are not obvious at all, when the ranks are bigger than 1. It is clear that
$$ \mathrm{srank}(T)\ge \mathrm{rank}(T).$$
Very recently, Shitov found an example where the strict inequality holds (see [1]).

Shitov’s example is quite peculiar: the tensor has dimension 3 and type $$800 \times 800 \times 800$$, whose rank is very high with respect of general tensors of same dimension and type.

The difficulty in finding examples where the two ranks are different, despite the large number of concrete tensors tested, suggested to the French mathematician Pierre Comon to launch the following:

Problem 7.2.7

(Comon 2000) Find conditions such that the symmetric rank and rank of a symmetric tensor coincide.

In other words, find conditions for $$T\in Sym^n(\mathbb C^d)$$ such that if there exists a decomposition $$T=T_1+\cdots + T_r$$ in terms of tensors of rank 1, then there exists also a decomposition with the same number of summands, in which each $$T_i$$ is symmetric, of rank 1.

The condition is known for some types of tensors. For instance, it is easy to prove that the Comon Problem holds for any symmetric matrix T (and this is left as an exercise at the end of the chapter).

The reader could wonder that such a question, which seems rather elementary in its formulation, could yield a problem which is still open, after being studied by many mathematicians, with modern techniques.

This explains a reason why, at the beginning of the chapter, we warned the reader that problems that are simple for Linear Algebra and matrices can suddenly become prohibitive, as the dimension of the tensors grows.

7.3 Symmetric Tensors and Polynomials

Homogeneous polynomials and symmetric tensors are two apparently rather different mathematical objects, that indeed have a strict interaction, so that one can skip from each other, translating properties of tensors to properties of polynomials, and vice versa.

The main construction behind this interaction is probably well known to the reader, for the case of polynomials of degree 2. It is a standard fact that one can associate a symmetric matrix to quadratic homogeneous polynomial, in a one-to-one correspondence, so that properties of the quadratic form (as well as properties of quadratic hypersurfaces) can be read as properties of the associated matrix.

The aim of this section is to point out that a similar correspondence holds, more generally, between homogeneous forms of any degree and symmetric tensors of higher dimension.

Definition 7.3.1

There is a natural map between a space $$K^{n,\dots ,n}$$ of cubic tensors of dimension d and the space of homogeneous polynomials of degree d in n variables (i.e., the dth graded piece $$R_d$$ of the ring of polynomials $$R=K[x_1,\dots ,x_n]$$), defined by sending a tensor T to the polynomial $$F_T$$ such that
$$ F_T = \sum _{i_1,\dots ,i_n} T_{i_1,\dots ,i_n} x_{i_1} \cdots x_{i_n} . $$
It is clear that the previous correspondence is not one to one, as soon as general tensors are considered. Namely, for the case $$n,d=2$$, one immediately sees that the two matrices
$$ \begin{pmatrix} 2 &{} 3 \\ -1 &{} 1 \end{pmatrix} \qquad \begin{pmatrix} 2 &{} 0 \\ 2 &{} 1 \end{pmatrix} $$
define the same polynomial of degree 2 in two variables $$F=2x_1^2+2x_1x_2+x_2^2$$.

The correspondence becomes one to one (and onto) when restricted to symmetric tensors. To see this, we need to introduce a piece of notation.

Definition 7.3.2

For any multi-index $$(i_1,\dots ,i_d)$$, we will define the multiplicity $$m(i_1,\dots ,i_d)$$ as the number of different permutations of the multi-index.

Definition 7.3.3

Let $$R=K[x_1,\dots ,x_n]$$ be the ring of polynomials, with coefficients in K, with n variables. Then there are linear isomorphisms
$$p: Sym^d(K^n)\rightarrow R_d \qquad t: R_d\rightarrow Sym^d(K^n)$$
defined as follows. The map p is the restriction to $$Sym^d(K^n)$$ of the previous map
$$p(T) = \sum _{i_1,\dots ,i_d} T_{i_1,\dots ,i_d} x_{i_1} \cdots x_{i_d}.$$
The map t is defined by sending the polynomial F to the tensor t(F) such that
$$ t(F)_{i_1,\dots ,i_d} = \frac{1}{m(i_1,\dots ,i_d)}({\text {the coefficient of }} x_{i_1}\cdots x_{i_d} {\text { in }} F).$$

Example 7.3.4

If G is a quadratic homogeneous polynomial in 3 variables $$G=Ax^2+Bxy+Cy^2+Dxz+Eyz+Fz^2$$, then t(G) is the symmetric matrix
$$ t(G)= \begin{pmatrix} A &{} B/2 &{} D/2 \\ B/2 &{} C &{} E/2 \\ D/2 &{} E/2 &{} F, \end{pmatrix}$$
which the usual matrix of the bilinear form associated to G.
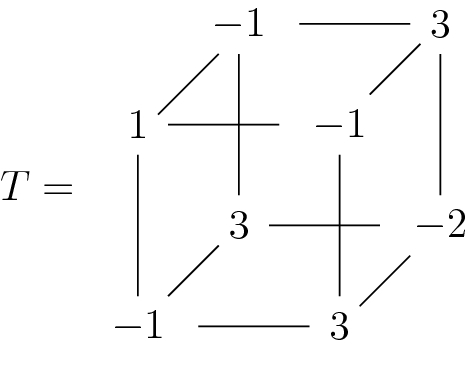
../images/485183_1_En_7_Chapter/485183_1_En_7_Figf_HTML.png

Example 7.3.5

Consider the homogeneous cubic polynomial in two variables
$$F(x_1,x_2) = x_1^3-3x_1^2x_2+9x_1x_2^2-2x_2^3.$$
Since one easily computes that
$$ m(1,1,1)=1,\ \ m(1,1,2) = m(2,1,1)= 3, \ \ m(2,2,2)=1,$$
then the symmetric tensor t(F) is:

It is an easy exercise to prove that the two maps p and t defined above are inverse to each other.

Once the correspondence is settled, one can easily speak about the rank or the the symmetric rank of a polynomial.

Definition 7.3.6

For any homogeneous polynomial $$G\in K[x_1,\dots ,x_n]$$, we define the rank  (respectively, the symmetric rank) of G as the rank (respectively, the symmetric rank) of the associated tensor t(G).

Example 7.3.7

The polynomial $$G= x_1^3+21x_1x_2^2+8x_2^3$$ has rank 3, since the associated tensor t(G) is exactly the $$2\times 2\times 2$$ symmetric tensor of Example 7.2.5.

Proposition 7.3.8

The linear space $$Sym^d(K^n)$$ has dimension
$$\dim (Sym^d(K^n)) = \left( {\begin{array}{c}n+d-1\\ d\end{array}}\right) = \left( {\begin{array}{c}n+d-1\\ n-1\end{array}}\right) .$$

Proof

This is obvious once one knows that $$\left( {\begin{array}{c}n+d-1\\ d\end{array}}\right) $$ is the dimension of the space of homogeneous polynomials $$R_d$$ of degree d in n variables. We prove it for the sake of completeness.

Since monomials of degree d in n variables are a basis for $$R_d$$, it is enough to count the number of such monomials.

The proof goes by induction on n. For $$n=2$$ the statement is easy: we have $$d+1$$ monomials, namely $$x_1^d, x_1^{d-1}x_2,\dots , x_2^d$$.

Assume the formula holds for $$n-1$$ variables $$x_2,\dots ,x_n$$. Every monomial of degree d in n variables is obtained by multiplying $$x_1^a$$ by any monomial of degree $$d-a$$ in $$x_2,\dots ,x_n$$. Thus, we have 1 monomial with $$x_1^d$$, n monomials with $$x_1^{d-1}$$,..., $$ \left( {\begin{array}{c}n+d-a-2\\ d-a\end{array}}\right) $$ monomials with $$x_1^a$$, and so on. Summing up
$$ \dim (Sym^d(K^n)) = \sum _{a=0}^d \left( {\begin{array}{c}n+d-a-2\\ d-a\end{array}}\right) ,$$
and the sum is $$\left( {\begin{array}{c}n+d-1\\ d\end{array}}\right) $$, by standard facts on binomial coefficients.$$\square $$

7.4 The Complexity of Polynomials

In this section, we rephrase the results on the rank of symmetric tensors in terms of the associated polynomials.

It will turn out that the rank decomposition of a polynomial is the analogue of a long-standing series of problems in Number Theory, for the expression of integers as a sum of powers.

In principle, from the point of view of Algebraic Statistic, the complexity of a polynomial is the complexity of the associated symmetric tensor. So, the most elementary case of polynomials corresponds to symmetric tensor of rank 1. We start with a description of polynomials of this type.

Remark 7.4.1

Before we proceed, we need to come back to the multiplicity of a multi-index $$J=(i_1,\dots ,i_d)$$, introduced in Definition 7.3.2.

In the correspondence between polynomials and tensors, the element $$T_{i_1,\dots ,i_d}$$ is linked with the coefficient of the monomial $$x_{i_1}\cdots x_{i_d}$$. Notice that $$i_1,\dots ,i_d$$ need not be distinct, so the monomial $$x_{i_1}\cdots x_{i_d}$$ could be written unproperly. The usual way in which $$x_{i_1}\cdots x_{i_d}$$ is written is:
$$ x_{i_1}\cdots x_{i_d} = x_1^{m_J(1)}x_2^{m_J(2)}\cdots x_n^{m_J(n)},$$
where $$m_J(i)$$ indicates the times in which i occurs in the multi-index J.
With the notation just introduced, one can describe the multiplicity $$m(i_1,\dots ,i_d)$$. Indeed a permutation changes the multi-index, unless it simply switches indices $$i_a,i_b$$ which are equal. Since the number of permutations over a set with m elements is m!, then one finds that
$$ m(J)=m(i_1,\dots ,i_d) = \frac{d!}{m_J(1)!\cdots m_J(n)!}. $$

Proposition 7.4.2

Let G be a homogeneous polynomial of degree d in n variables, so that $$t(G)\in Sym^d(K^n)$$.

Then t(G) has rank 1 if and only if there exists a homogeneous linear polynomial $$L\in K[x_1,\dots ,x_n]$$, such that $$G=L^d$$.

Proof

It is sufficient to prove that $$t(G)= v^{\otimes d}$$, where $$v=(\alpha _1,\dots ,\alpha _n) \in K^n$$, if and only if $$G=(\alpha _1x_1+\cdots +\alpha _nx_n)^d$$.

To this aim, just notice that the coefficient of the monomial $$x_1^{m_1}\cdots x_n^{m_n}$$ in $$p(v^{\otimes d})$$ is the sum of the entries of the tensors $$ v^{\otimes d}$$ whose multi-index J satisfies $$m_J(1)=m_1,\dots , m_J(n)=m_n$$. These entries are all equal to $$\alpha _1^{m_1}\cdots \alpha _n^{m_n}$$ and their number is m(J). On the other hand, by the well-known Newton formula, $$m(J)(\alpha _1^{m_1}\cdots \alpha _n^{m_n})$$ is exactly the coefficient of the monomial $$x_1^{m_1}\cdots x_n^{m_n}$$ in the power $$(\alpha _1x_1+\cdots + \alpha _nx_n)^d$$.

Corollary 7.4.3

The symmetric rank of a homogeneous polynomial $$G\in K[x_1,\dots ,x_n]_d$$ is the minimum r for which there are r linear homogeneous forms $$L_1,\dots ,L_r\in K[x_1,\dots ,x_n]$$, with
$$\begin{aligned} G = L_1^d+\cdots + L_r^d.\end{aligned}$$
(7.1)

The symmetric rank is the number that computes the complexity of symmetric tensors, hence the complexity of homogeneous polynomials, from the point of view of Algebraic Statistics. Hence, it turns out that the simplest polynomials, in this sense, are powers of linear forms. We guess that nobody will object to the statement that powers are rather simple!

We should mention, however, that sometimes the behavior of polynomials with respect to the complexity can be much less intuitive.

For instance, the rank of monomials is usually very high, so that the complexity of general monomials is over the average (and we expect that most people will be surprised). Even worse, efficient formulas for the rank of monomials were obtained only very recently by Enrico Carlini, Maria Virginia Catalisano, and Anthony V. Geramita (see [2]). For other famous polynomials, as the determinant of a matrix of indeterminates, we do not even know the rank. All we have are lower and upper bounds, not matching.

We finish the chapter by mentioning that the problem of finding the rank of polynomials reflects a well-known problem in Number Theory. Solving a question posed by Diophantus, the Italian mathematician Giuseppe Lagrange proved that any positive integer N can be written as a sum of four squares, i.e., for any positive integer G, there are integers $$L_1,L_2,L_3,L_4$$ such that $$ G =L_1^2+L_2^2+L_3^2+L_4^2.$$ The problem has been generalized by the English mathematician Edward Waring, who asked in 1770 for the minimum integer r(k) such that any positive integer G can be written as a sum of r(k) powers $$L_i^k$$. In other words, find the minimum r(k) such that any positive integers are of the form
$$ G =L_1^k+\cdots L_{r(k)}^k.$$
The analogy with the decomposition (7.1) that computes the symmetric rank of a polynomial is evident.

The determination of r(k) is called, from then, the Waring problem  for integers. Because of the analogy, the symmetric rank of a polynomial is also called the Waring rank.

For integers, few values of r(k) are known, e.g., $$r(2)=4$$, $$r(3)=9$$, $$r(4)=19$$. There are also variations on the Waring problem, as asking for the minimum $$r'(k)$$ such that all positive integers, except for a finite subset, are the sum of $$r'(k)$$ kth powers (the little Waring problem).

Going back to the polynomial case, as for integers, a complete description of the maximal complexity that a homogeneous polynomial of the given degree in a given number of variables can have, is not known. We have only upper bounds for the maximal rank. On the other hand, we know the solution of an analogue to the little Waring problem, for polynomials over the complex field.

Theorem 7.4.4

(Alexander-Hirschowitz 1995)  Over the complex field, the symmetric rank of a general homogeneous polynomial of degree d in n variables (here general means: all polynomials outside a set of measure 0 in $$\mathbb C[x_1,\dots ,x_n]_d$$; or also: all polynomials outside a Zariski closed subset of the space $$\mathbb C[x_1,\dots ,x_n]_d$$, see Remark 9.​1.​10) is
$$ r =\lceil \frac{\left( {\begin{array}{c}n+d-1\\ d\end{array}}\right) }{n}\rceil $$
except for the following cases:

  • $$d=2$$, any n, where $$r=n$$;

  • $$d=3$$, $$n=5$$, where $$r=8$$;

  • $$d=4$$, $$n=3$$, where $$r=6$$.

  • $$d=4$$, $$n=4$$, where $$r=10$$.

  • $$d=4$$, $$n=5$$, where $$r=15$$.

The original proof of this theorem requires the Horace method. It is long and difficult and occupies a whole series of papers [3–7].

For specific tensors, an efficient way to compute the rank requires the use of inverse systems, which will be explained in the next chapter.

7.5 Exercises

Exercise 11

Prove that the two maps p and t introduced in Definition 7.3.3 are linear and inverse to each other.

Exercise 12

Prove Comon’s Problem for matrices: a symmetric matrix M has rank r if and only if there are r symmetric matrices of rank 1, $$M_1$$,..., $$M_r$$, such that $$M=M_1+\cdots +M_r$$.

Exercise 13

Prove that the tensor T of Example 7.2.5 cannot have rank 2.

Exercise 14

Prove that the tensor T of Example 7.2.5 has symmetric rank $$\mathrm{srank}(T)=3$$ (so, after Exercise 13, also the rank is 3).