Appendix E

The Mathematics of RSA

What follows is a straightforward mathematical description of the mechanics of RSA encryption and decryption.

1. Alice picks two giant prime numbers, p and q. The primes should be enormous, but for simplicity we assume that Alice chooses p = 17, q = 11. She must keep these numbers secret.

2. Alice multiplies them together to get another number, N. In this case N = 187. She now picks another number e, and in this case she chooses e = 7 (e and (p – 1) x (q – 1) should be relatively prime, but this is a technicality).

3. Alice can now publish e and N in something akin to a telephone directory. Since these two numbers are necessary for encryption, they must be available to anybody who might want to encrypt a message to Alice. Together these numbers are called the public key. (As well as being part of Alice’s public key, e could also be part of everybody else’s public key. However, everybody must have a different value of N, which depends on their choice of p and q.)

4. To encrypt a message, the message must first be converted into a number, M. For example, a word is changed into ASCII binary digits, and the binary digits can be considered as a decimal number. M is then encrypted to give the ciphertext, C, according to the formula C = M^e (mod N).

5. Imagine that Bob wants to send Alice a simple kiss: just the letter X. In ASCII this is represented by 1011000, which is equivalent to 88 in decimal. So, M = 88.

6. To encrypt this message, Bob looks up Alice’s public key, and discovers that N = 187 and e =7. This provides him with the encryption formula required to encrypt messages to Alice. With M = 88, the formula gives C = 88⁷ (mod 187).

7. Working this out directly on a calculator is tough, because the display cannot cope with such large numbers. However, there is a trick for calculating exponentials in modular arithmetic. We know that since 7 = 4 + 2 + 1,

Bob now sends the ciphertext, C = 11, to Alice.

8. We know that exponentials in modular arithmetic are one-way functions, so it is very difficult to work backwards from C = 11 and recover the original message, M. Hence, Eve cannot decipher the message.

9. However, Alice can decipher the message because she has some special information: she knows the values of p and q. She calculates a special number, d, the decryption key, otherwise known as her private key. The number d is calculated according to the following formula:

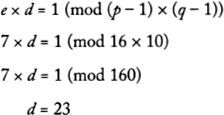
(Deducing the value of d is not straightforward, but a technique known as Euclid’s algorithm allows Alice to find d quickly and easily.)

10. To decrypt the message, Alice uses this formula:

Rivest, Shamir and Adleman had created a special one-way function, one that could be reversed only by somebody with access to privileged information, namely, the values of p and q. Each function can be personalized by choosing p and q, which multiply together to give N.

Having described RSA in terms of encrypting a message letter by letter, it is necessary to clarify one particular point. In the previous example, RSA is effectively reduced to monoalphabetic substitution without key distribution. In practice, encryption would proceed according to much larger blocks of binary digits, thus making frequency analysis impossible.