6

ORGANIZING INFORMATION FOR THE HARDEST DECISIONS

When Life Is on the Line

Nothing comes to my desk that is perfectly solvable,” President Obama observed. “Otherwise, someone else would have solved it.”

Any decision for which the solution is obvious—a no-brainer—is going to be made by someone lower down the line than the president. No one wants to waste his, which is after all our, valuable time. The only decisions that come to him are the ones that have stumped everyone down the line before him.

Most of the decisions that a president of the United States has to make have serious implications—potential loss of life, escalation of tensions between countries, changes in the economy that could lead to loss of jobs. And they typically arrive with impoverished or imperfect information. His advisors don’t need him to brainstorm about new possibilities—although occasionally he may do that. The advisors pass a problem upward not because they’re not smart enough to solve it, but because it invariably involves a choice between two losses, two negative outcomes, and the president has to decide which is more palatable. At that point, President Obama says, “you wind up dealing with probabilities. Any given decision you make, you’ll wind up with a thirty to forty percent chance that it isn’t going to work.”

I wrote about Steve Wynn, the CEO of Wynn Resorts, in Chapter 3. About decision-making, he says, “In any sufficiently large organization, with an effective management system in place, there is going to be a pyramid shape with decision makers at every level. The only time I am brought in is when the only known solutions have a downside, like someone losing their job, or the company losing large sums of money. And usually the decision is already framed for me as two negatives. I’m the one who has to choose which of those two negatives we can live with.”

Medical decision-making often feels a lot like that—choosing between two negatives. We face a gamble: either the possibility of declining health if we do nothing, or great potential discomfort, pain, and expense if we choose a medical procedure. Trying to evaluate the outcomes rationally can be taxing.

Most of us are ill-equipped to calculate such probabilities on our own. We’re not just ill-equipped to calculate probabilities, we are not trained to evaluate them rationally. We’re faced with decisions every day that impact our livelihood, our happiness, and our health, and most of these decisions—even if we don’t realize it at first—come down to probabilities. If a physician starts explaining medical choices probabilistically, it is likely the patient will not grasp the information in a useful way. The news is delivered to us during a period of what can be extreme emotional vulnerability and cognitive overload. (How do you feel when you get a diagnosis?) While the physician is explaining a 35% chance of this and a 5% chance of that, our minds are distracted, racing with thoughts of hospital bills and insurance, and how we’ll ask for time off work. The doctor’s voice fades into the background as we imagine pain, discomfort, whether our will is up to date, and who’s going to look after the dog while we’re in the hospital.

This chapter provides some simple tools for organizing information about health care, and they apply to all the hardest decisions we face. But the complexity of medical information inevitably provokes strong emotions while we grapple with unknowns and even the meaning of our lives. Medical decision-making presents a profound challenge to the organized mind, no matter how many assistants you have, or how competent you are at everything else you do.

Thinking Straight About Probabilities

Decision-making is difficult because, by its nature, it involves uncertainty. If there was no uncertainty, decisions would be easy! The uncertainty exists because we don’t know the future, we don’t know if the decision we make will lead to the best possible outcome. Cognitive science has taught us that relying on our gut or intuition often leads to bad decisions, particularly in cases where statistical information is available. Our guts and our brains didn’t evolve to deal with probabilistic thinking.

Consider a forty-year-old woman who wants to have children. She reads that, compared to someone younger, she is five times more likely to have a child with a particular birth defect. At first glance, this seems like an unacceptable risk. She is being asked to pit her strong emotional desire for children against an intellectual knowledge of statistics. Can knowledge of statistics bridge this gap and lead her to the right conclusion, the one that will give her the happiest life?

Part of maintaining an organized mind and organized life requires that we make the best decisions possible. Bad decisions sap strength and energy, not to mention the time we might have to invest in revisiting the decision when things go wrong. Busy people who make a lot of high-stakes decisions tend to divide their decision-making into categories, performing triage, similar to what I wrote about for list making and list sorting in Chapter 3:

1. Decisions you can make right now because the answer is obvious
2. Decisions you can delegate to someone else who has more time or expertise than you do
3. Decisions for which you have all the relevant information but for which you need some time to process or digest that information. This is frequently what judges do in difficult cases. It’s not that they don’t have the information—it’s that they want to mull over the various angles and consider the larger picture. It’s good to attach a deadline to these.
4. Decisions for which you need more information. At this point, either you instruct a helper to obtain that information or you make a note to yourself that you need to obtain it. It’s good to attach a deadline in either case, even if it’s an arbitrary one, so that you can cross this off your list.

Medical decision-making sometimes falls into category 1 (do it now), such as when your dentist tells you that you have a new cavity and she wants to fill it. Fillings are commonplace and there is not much serious debate about alternatives. You probably have had fillings before, or know people who have, and you’re familiar with the procedures. There are risks, but these are widely considered to be outweighed by the serious complications that could result from leaving the cavity unfilled. The word widely here is important; your dentist doesn’t have to spend time explaining alternatives or the consequences of not treating. Most physicians who deal with serious diseases don’t have it this easy because of the uncertainty about the best treatment.

Some medical decision-making falls into category 2 (delegate it), especially when the literature seems either contradictory or overwhelming. We throw up our hands and ask, “Doc, what would you do?” essentially delegating the decision to her.

Category 3 (mull it over) can seem like the right option when the problem is first presented to you, or after categories 2 and 4 (get more information) have been implemented. After all, for decisions that affect our time on this planet, it is intuitively prudent not to race to a decision.

Much of medical decision-making falls into category 4—you simply need more information. Doctors can provide some of it, but you’ll most likely need to acquire additional information and then analyze it to come to a clear decision that’s right for you. Our gut feelings may not have evolved to deal instinctively with probabilistic thinking, but we can train our brain in an afternoon to become a logical and efficient decision-making machine. If you want to make better medical decisions—particularly during a time of crisis when emotional exhaustion can cloud the decision-making process—you need to know something about probabilities.

We use the term probability in everyday conversation to refer to two completely different concepts, and it’s important to separate these. In one case, we are talking about a mathematical calculation that tells us the likelihood of a particular outcome from among many possible ones—an objective calculation. In the other case, we’re referring to something subjective—a matter of opinion.

Probabilities of the first kind describe events that are calculable or countable, and—importantly—they are theoretically repeatable. We might be describing events such as tossing a coin and getting three heads in a row, or drawing the king of clubs from a deck of cards, or winning the state lottery. Calculable means we can assign precise values in a formula and generate an answer. Countable means we can determine the probabilities empirically by performing an experiment or conducting a survey and counting the results. To say that they’re repeatable simply means we can do the experiment over and over again and expect similar descriptions of the probabilities of the events in question.

For many problems, calculating is easy. We consider all possible outcomes and the outcome we’re interested in and set up an equation. The probability of drawing the king of clubs (or any other single card) from a full deck is 1 out of 52 because it is possible to draw any of the 52 cards in a deck and we’re interested in just 1 of them. The probability of picking any king from a full deck is 4 out of 52 because there are 52 cards in the deck and we’re interested in 4 of them. If there are 10 million tickets sold in a fresh round of a sweepstakes and you buy 1 ticket, the probability of your winning is 1 out of 10 million. It’s important to recognize, both in lotteries and medicine, you can do things that change a probability by a large amount but with no real-world, practical significance. You can increase the odds of winning that state lottery by a factor of 100 by buying 100 lottery tickets. But the chance of winning remains so incredibly low, 1 in 100,000, that it hardly seems like a reasonable investment. You might read that the probability of getting a disease is reduced by 50% if you accept a particular treatment. But if you only had a 1 in 10,000 chance of getting it anyway, it may not be worth the expense, or the potential side effects, to lower the risk.

Some probabilities of the objective type are difficult to calculate, but they are countable, at least in principle. For example, if a friend asked you the probability of drawing a straight flush—any sequence of five cards of the same suit—you might not know how to work this out without consulting a probability textbook. But in theory, you could count your way to an answer. You would deal cards out of decks all day long for many days and simply write down how often you get a straight flush; the answer would be very close to the theoretical probability of .0015% (15 chances in 1,000,000). And the longer you make the experiment—the more trials you have—the closer your counted observations are likely to come to the true, calculated probability. This is called the law of large numbers: Observed probabilities tend to get closer and closer to theoretical ones when you have larger and larger samples. The big idea is that the probability of getting a straight flush is both countable and repeatable: If you get friends to perform the experiment, they should come up with similar results, provided they perform the experiment long enough for there to be a large number of trials.

Other kinds of outcomes are not even theoretically calculable, but are still countable. The probability of a baby being born a boy, of a marriage ending in divorce, and of a house on Elm Street catching fire all fall into this category. For questions like these, we resort to observations—we count because there’s no formula that tells us how to calculate the probability. We check the records of births in area hospitals, we look at fire reports over a ten-year period in the neighborhood. An automobile manufacturer can obtain failure data from hundreds of thousands of fuel injectors to find out the probability of failure after a given amount of use.

Whereas objective probabilities involve a calculation from theory or counting from observation, the second kind of probability—the subjective—is neither calculable nor countable. In this case, we are using the word probability to express our subjective confidence in a future event. For example, if I say there is a 90% chance that I’m going to Susan’s party next Friday, this wasn’t based on any calculation I performed or indeed that anyone could perform—there is nothing to measure or calculate. Instead, it is an expression of how confident I am that this outcome will occur. Assigning numbers like this gives the impression that the estimate is precise, but it isn’t.

So even though one of these two kinds of probability is objective and the other is subjective, almost nobody notices the difference—we use the word probability in everyday speech, blindly going along with it, and treating the two different kinds of probability as the same thing.

When we hear things like “There is a sixty percent chance that the conflict between these two countries will escalate to war” or “There is a ten percent probability that a rogue nation will detonate an atomic device in the next ten years,” these are not calculated probabilities of the first kind; they are subjective expressions of the second kind, about how confident the speaker is that the event will occur. Events of this second kind are not replicable like the events of the first kind. And they’re not calculable or countable like playing cards or fires on Elm Street. We don’t have a bunch of identical rogue nations with identical atomic devices to observe to establish a count. In these cases, a pundit or educated observer is making a guess when they talk about “probability,” but it is not a probability in the mathematical sense. Competent observers may well disagree about this kind of probability, which speaks to their subjectivity.

Drawing the king of clubs two times in a row is unlikely. Just how unlikely? We can calculate the probability of two events occurring by multiplying the probability of one event by the probability of the other. The probability of drawing the king of clubs from a full deck is ¹⁄₅₂ for both the first and second drawing (if you put the first king back after drawing it, to make the deck full again). So ¹⁄₅₂ × ¹⁄₅₂ = ¹⁄₂₇₀₄. Similarly, the probability of getting three heads in a row in tossing a coin is calculated by taking the probability of each event, ¹/₂, and multiplying them together three times: ¹/₂ × ¹/₂ × ¹/₂ = ¹⁄₈. You could also set up a little experiment where you toss a coin three times in a row many times. In the long run, you’ll get three heads in a row about one-eighth of the time.

For this multiplication rule to work, the events have to be independent. In other words, we assume that the card I draw the first time doesn’t have anything to do with the card I draw the second time. If the deck is shuffled properly, this should be true. Of course there are cases when the events are not independent. If I see that you put the king of clubs on the bottom of the deck after my first pick, and I choose the bottom of the deck the second time, the events aren’t independent. If a meteorologist forecasts rain today and rain tomorrow, and you want to know the probability that it will rain two days in a row, those events are not independent, because weather fronts take some time to pass through an area. If the events are not independent, the math gets a bit more complicated—although not terribly so.

Independence needs to be considered carefully. Getting struck by lightning is very unusual—according to the U.S. National Weather Service, the chance is 1 in 10,000. So, is the chance of getting struck by lightning twice 1/10,000 × 1/10,000 (1 chance in 100 million)? That holds only if the events are independent, and they probably are not. If you live in an area with a lot of lightning storms and you tend to stay outdoors during them, you are more likely to be struck by lightning than someone who lives in a different locale and takes more precautions. One man was hit by lightning twice within two minutes, and a Virginia park ranger was hit seven times during his lifetime.

It would be foolish to say, “I’ve already been hit by lightning once, so I can walk around in thunderstorms with impunity.” Yet this is the sort of pseudo logic that is trotted out by people unschooled in probability. I overheard a conversation at a travel agency some years ago as a young couple were trying to decide which airline to fly. It went something like this (according to my no doubt imperfect memory):

Alice: “I’m not comfortable taking Blank Airways—they had that crash last year.”

Bob: “But the odds of a plane crash are one in a million. Blank Airways just had their crash. It’s not going to happen to them again.”

Without knowing more about the circumstances of the Blank Airways crash, Alice’s statement indeed constitutes a perfectly reasonable fear. Airplane crashes are usually not random events; they potentially indicate some underlying problem with an airline’s operations—poorly trained pilots, careless mechanics, an aging fleet. The likelihood of Blank Airways having two crashes in a row cannot be considered independent events. Bob is using “gut reasoning” and not logical reasoning, like saying that since you just got hit by lightning, it can’t happen again. Following this pseudologic to an extreme, you can imagine Bob arguing, “The chances of a bomb being on this plane are one in a million. Therefore I’ll bring a bomb on the plane with me because the chance of two bombs being on the plane are astronomically high.”

Even if plane crashes were independent, to think that it won’t happen now “because it just happened” is to fall for a form of the gambler’s fallacy, thinking that a safe flight is now “due.” The gods of chance are not counting flights to make sure that one million go by before the next crash, and neither are they going to ensure that the next crashes are evenly distributed among the remaining air carriers. So the likelihood of any airline having two crashes in a row cannot be considered independent.

An objectively obtained probability is not a guarantee. Although in the long run, we expect a coin to come up heads half the time, probability is not a self-correcting process. The coin has no memory, knowledge, willpower, or volition. There is not some overlord of the theory of probability making sure that everything works out just the way you expect. If you get “heads” ten times in a row, the probability of the coin coming up “tails” on the next toss is still 50%. Tails is not more likely and it is not “due.” The notion that chance processes correct themselves is part of the gambler’s fallacy, and it has made many casino owners, including Steve Wynn, very wealthy. Millions of people have continued to put money into slot machines under the illusion that their payout is due. It’s true that probabilities tend to even out, but only in the long run. And that long run can take more time and money than anyone has.

The confusing part of this is that our intuition tells us that getting eleven heads in a row is very unlikely. That is right—but only partially right.

The flaw in the reasoning results from confusing the rarity of ten heads in a row with the rarity of eleven heads in a row—in fact, they are not all that different. Every sequence of ten heads in a row has to be followed by either another head or another tail, each of which is equally likely.

Humans have a poor sense of what constitutes a random sequence. When asked to generate a random sequence, we tend to write down far more alternations (heads—tails—heads—tails) and far fewer runs (heads—heads—heads) than appear in actual random sequences. In one experiment, people were asked to write down what they thought a random sequence would look like for 100 tosses of a coin. Almost no one put down runs of seven heads or tails in a row, even though there is a greater than 50% chance that they will occur in 100 tosses. Our intuition pushes us toward evening out the heads/tails ratio even in short sequences, although it can take very long sequences—millions of tosses—for the stable 50/50 ratio to show up.

Fight that intuition! If you toss a coin three times in a row, it is true that there is only a 1/8 chance that you’ll get three heads in a row. But this is confounded by the fact that you’re looking at a short sequence. On average, only 14 flips are required to get three heads in a row, and in 100 flips, there’s a greater than 99.9% chance there will be three heads in a row at least once.

The reason we get taken in by this illogical thinking—the thinking that probabilities change in sequences—is that in some cases they do actually change. Really! If you’re playing cards and you’ve been waiting for an ace to show up, the probability of an ace increases the longer you wait. By the time 48 cards have been dealt, the probability of an ace on the next card is one (all that is left are aces). If you’re a hunter-gatherer searching for that stand of fruit trees you saw last summer, each section of land you search without finding it increases your chance of finding it in the next one. Unless you stop to think carefully, it is easy to confuse these different probability models.

Many things we are interested in have happened before, and so we can usually count or observe how often they tend to occur. The base rate of something is the background rate of its occurrence. Most of us have an intuitive sense for this. If you bring your car to the mechanic because the engine is running rough, before even looking at it, your mechanic might say something like “It’s probably the timing—that’s what it is in ninety percent of the cars we see. It could also be a bad fuel injector, but the injectors hardly ever fail.” Your mechanic is using informed estimations of the base rate that something occurs in the world.

If you’re invited to a party at Susan’s house with a bunch of people you’ve never met, what are the chances that you’ll end up talking to a doctor versus a member of the president’s cabinet? There are many more doctors than there are cabinet members. The base rate for doctors is higher, and so if you know nothing at all about the party, your best guess is you’ll run into more doctors than cabinet members. Similarly, if you suddenly get a headache and you’re a worrier, you may fear that you have a brain tumor. Unexplained headaches are very common; brain tumors are not. The cliché in medical diagnostics is “When you hear hoofbeats, think horses, not zebras.” In other words, don’t ignore the base rate of what is most likely, given the symptoms.

Cognitive psychology experiments have amply demonstrated that we typically ignore base rates in making judgments and decisions. Instead, we favor information we think is diagnostic, to use a medical term. At Susan’s party, if the person you’re talking to has an American flag lapel pin, is very knowledgeable about politics, and is being trailed by a U.S. Secret Service agent, you might conclude that she is a cabinet member because she has the attributes of one. But you’d be ignoring base rates. There are 850,000 doctors in the United States and only fifteen cabinet members. Out of 850,000 doctors, there are bound to be some who wear American flag label pins, are knowledgeable about politics, and are even trailed by the Secret Service for one reason or another. For example, sixteen members of the 111th Congress were doctors—far more than there are cabinet members. Then there all the doctors who work for the military, the FBI, and the CIA, and doctors whose spouses, parents, or children are high-profile public servants—some of whom may qualify for Secret Service protection. Some of those 850,000 doctors may be up for security clearances or are being investigated in some matter, which would account for the Secret Service agent. This error in reasoning is so pervasive that it has a name—the representativeness heuristic. It means that people or situations that appear to be representative of one thing effectively overpower the brain’s ability to reason, and cause us to ignore the statistical or base rate information.

In a typical experiment from the scientific literature, you’re given a scenario to read. You’re told that in a particular university, 10% of the students are engineers and 90% are not. You go to a party and you see someone wearing a plastic pocket protector (unstated in the description is that many people consider this a stereotype for engineers). Then you’re asked to rate how likely you think it is that this person is an engineer. Many people rate it as a certainty. The pocket protector seems so diagnostic, such conclusive evidence, that it is hard to imagine that the person could be anything else. But engineers are sufficiently rare in this university that we need to account for that fact. The probability of this person being an engineer may not be as low as the base rate, 10%, but it is not as high as 100%, either—other people might wear pocket protectors, too.

Here’s where it gets interesting. Researchers then set up the same scenario—a party at a university where 10% of the students are engineers and 90% are not—and then explain: “You run into someone who might be wearing a plastic pocket protector or not, but you can’t tell because he has a jacket on.” When asked to rate the probability that he is an engineer, people typically say “fifty-fifty.” When asked to explain why, they say, “Well, he could be wearing a pocket protector or not—we don’t know.” Here again is a failure to take base rates into account. If you know nothing at all about the person, then there is a 10% chance he is an engineer, not a 50% chance. Just because there are only two choices doesn’t mean they are equally likely.

To take an example that might be intuitively clearer, imagine you walk into your local grocery store and bump into someone without seeing them. It could either be Queen Elizabeth or not. How likely is it that it is Queen Elizabeth? Most people don’t think it is 50-50. How likely is it that the queen would be in any grocery store, let alone the one I shop at? Very unlikely. So this shows we’re capable of using base rate information when events are extremely unlikely. It’s when they’re only mildly unlikely that our brains freeze up. Organizing our decisions requires that we combine the base rate information with other relevant diagnostic information. This type of reasoning was discovered in the eighteenth century by the mathematician and Presbyterian minister Thomas Bayes, and bears his name: Bayes’s rule.

Bayes’s rule allows us to refine estimates. For example, we read that roughly half of marriages end in divorce. But we can refine that estimate if we have additional information, such as the age, religion, or location of the people involved, because the 50% figure holds only for the aggregate of all people. Some subpopulations of people have higher divorce rates than others.

Remember the party at the university with 10% engineers and 90% non-engineers? Some additional information could help you to estimate the probability that someone with a pocket protector is an engineer. Maybe you know that the host of the party had a bad breakup with an engineer, so she no longer invites them to her parties. Perhaps you learn that 50% of premed and medical students at this school wear pocket protectors. Information like this allows us to update our original base rate estimates with the new information. Quantifying this updated probability is an application of Bayesian inferencing.

We’re no longer asking the simple, one-part question “What is the probability that the person with a pocket protector is an engineer?” Instead, we’re asking the compound question “What is the probability that the person with a pocket protector is an engineer, given the information that fifty percent of the premeds and medical students at the school wear pocket protectors?” The rarity of engineers is being pitted against the added circumstantial information about the ubiquity of pocket protectors.

We can similarly update medical questions such as “What is the likelihood that this sore throat indicates the flu, given that three days ago I visited someone who had the flu?” or “What is the likelihood that this sore throat indicates hay fever, given that I was just outdoors gardening at the height of pollen season?” We do this kind of updating informally in our heads, but there are tools that can help us to quantify the effect of the new information. The problem with doing it informally is that our brains are not configured to generate accurate answers to these questions intuitively. Our brains evolved to solve a range of problems, but Bayesian problems are not among them yet.

Oh, No! I Just Tested Positive!

How serious is news like this? Complex questions like this are easily solvable with a trick I learned in graduate school—fourfold tables (also known as contingency tables). They are not easily solved using intuition or hunches. Say you wake up with blurred vision one morning. Suppose further that there exists a rare disease called optical blurritis. In the entire United States, only 38,000 people have it, which gives it an incidence, or base rate, of 1 in 10,000 (38,000 out of 380 million). You just read about it and now you fear you have it. Why else, you are thinking, would I have blurry vision?

You take a blood test for blurritis and it comes back positive. You and your doctor are trying to decide what to do next. The problem is that the cure for blurritis, a medication called chlorohydroxelene, has a 5% chance of serious side effects, including a terrible, irreversible itching just in the part of your back that you can’t reach. (There’s a medication you can take for itching, but it has an 80% chance of raising your blood pressure through the roof.) Five percent doesn’t seem like a big chance, and maybe you’re willing to take it to get rid of this blurry vision. (That 5% is an objective probability of the first kind—not a subjective estimate but a figure obtained from tracking tens of thousands of recipients of the drug.) Naturally, you want to understand precisely what the chances are that you actually have the disease before taking the medication and running the risk of being driven crazy with itching.

The fourfold table helps to lay out all this information in a way that’s easy to visualize, and doesn’t require anything more complicated than eighth-grade division. If numbers and fractions make you want to run screaming from the room, don’t worry—the Appendix contains the details, and this chapter gives just a birds’-eye view (a perhaps blurry one, since after all, you’re suffering from the symptoms of blurritis right now).

Let’s look at the information we have.

• The base rate for blurritis is 1 in 10,000, or .0001.
• Chlorohydroxelene use ends in an unwanted side effect 5% of the time, or .05.

You might assume that if the test came back positive, it means you have the disease, but tests don’t work that way—most are imperfect. And now that you know something about Bayesian thinking, you might want to ask the more refined question “What is the probability that I actually have the disease, given that the test came out positive?” Remember, the base rate tells us that the probability of having the disease for anyone selected at random is .0001. But you’re not just anyone selected at random. Your vision was blurry, and your doctor had you take the test.

We need more information to proceed. We need to know what percentage of the time the test is wrong, and that it can be wrong in two ways. It can indicate you have the disease when you don’t—a false positive—or it can indicate that you don’t have the disease when you do—a false negative. Let’s assume that both of these figures are 2%. In real life, they can be different from each other, but let’s assume 2% for each.

We start by drawing four squares and labeling them like this:

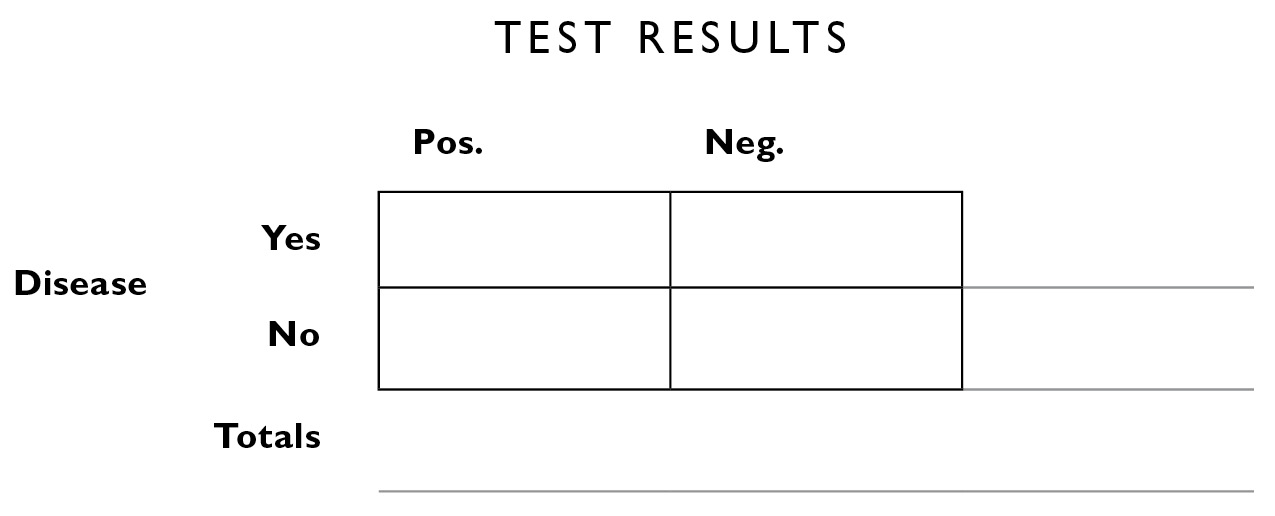
The column headings represent the fact that the test result can be either positive or negative. We set aside for the moment whether those results are accurate or not—that’s what we’ll use the table to conclude. The row headings show that the disease can be either present or absent in a given patient. Each square represents a conjunction of the row and column headings. Reading across, we see that, of the people who have the disease (the “Disease yes” row), some of them will have positive results (the ones in the upper left box) and some will have negative test results (the upper right box). The same is true of the “Disease no” row; some people will have positive test results and some will have negative. You’re hoping that even though you tested positive (the left column), you don’t have the disease (the lower left square).

After filling in the information we were given (I walk through it more slowly in the Appendix), we can answer the question “What is the probability that I have the disease, given that I had a positive test result?”

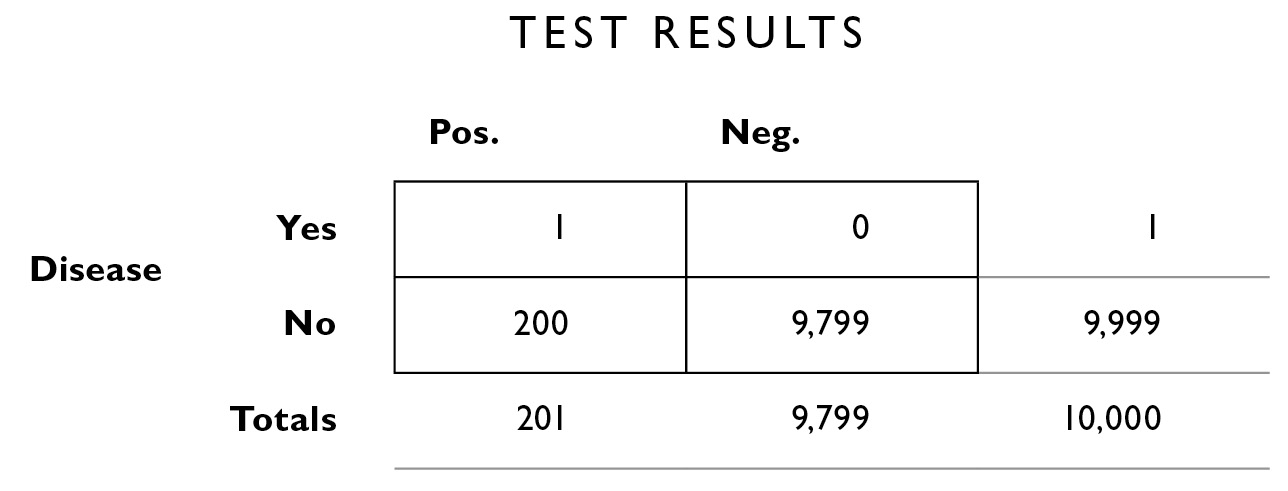
Consider the column that shows people who have a positive test result:

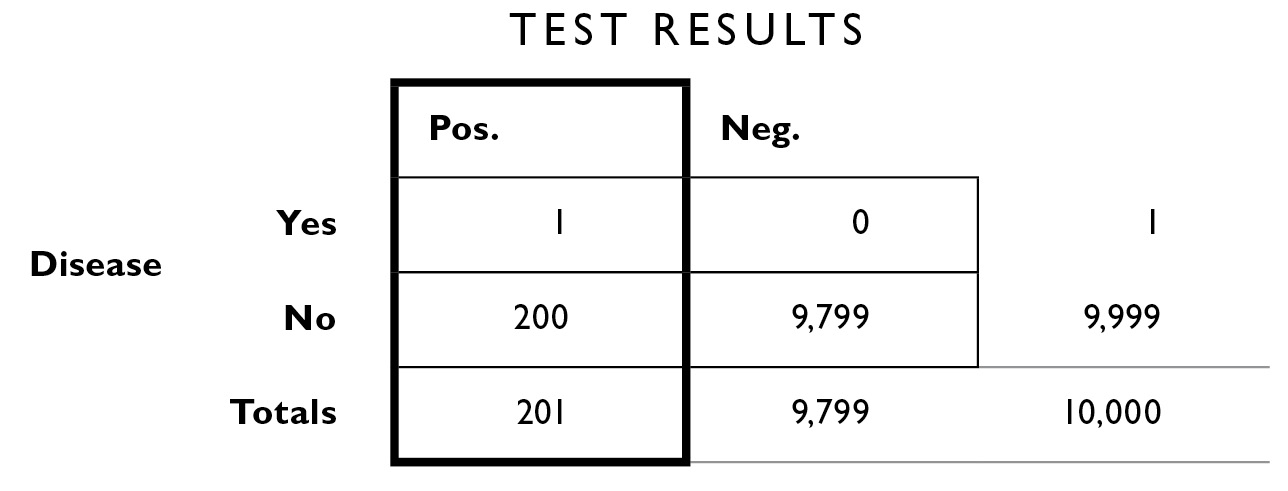
You can see that out of 10,000 people, 201 of them (the total in the margin below the left column) had a positive test result like yours. But of those 201 people, only 1 has the disease—there is only 1 chance in 201 that you actually have the disease. We can take 1/201 × 100 to turn it into a percent, and we obtain about 0.49%—not a high likelihood however you put it. . . . Your chances were 1 in 10,000 before you went in for the test. Now they are 1 in 201. There is still a roughly 99.51% chance you do not have the disease. If this reminds you of the lottery ticket example above, it should. Your odds have changed dramatically, but this hasn’t affected the real-world outcome in any appreciable way. The take-home lesson is that the results of the test don’t tell you everything you need to know—you need to also apply the base rate and error rate information to give you an accurate picture. This is what the fourfold table allows you to do. It doesn’t matter whether the disease produces moderate symptoms, such as blurry vision, or very severe symptoms, such as paralysis; the table still allows you to organize the information in an easily digestible format. Ideally, you would also work closely with your physician to take into account any comorbid conditions, co-occurring symptoms, family history, and so on to make your estimate more precise.

Let’s look at that other piece of information, the miracle drug that can cure blurritis, chlorohydroxelene, which has a 1 in 5 chance of side effects (20% side effects is not atypical for real medications). If you take the medicine, you need to compare the 1 in 5 chance of a relentlessly itchy back with the 1 in 201 chance that it will offer you a cure. Put another way, if 201 people take the drug, only 1 of them will experience a cure (because 200 who are prescribed the drug don’t actually have the disease—yikes!). Now, of those same 201 people who take the drug, 1 in 5, or 40, will experience the side effect. So 40 people end up with that back itch they can’t reach, for every 1 person who is cured. Therefore, if you take the drug, you are 40 times more likely to experience the side effect than the cure. Unfortunately, these numbers are typical of modern health care in the United States. Is it any wonder that costs are skyrocketing and out of control?

One of my favorite examples of the usefulness of fourfold tables comes from my teacher Amos Tversky. It’s called the two-poison problem. When Amos administered a version of it to MDs at major hospitals and medical schools, as well as to statisticians and business school graduates, nearly every one of them got the answer so wrong that the hypothetical patients would have died! His point was that probabilistic reasoning doesn’t come naturally to us; we have to fight our knee-jerk reaction and learn to work out the numbers methodically.

Imagine, Amos says, that you go out to eat at a restaurant and wake up feeling terrible. You look in the mirror and see that your face has turned blue. Your internist tells you that there are two food-poisoning diseases, one that turns your face blue and one that turns your face green (we assume for this problem that there are no other possibilities that will turn your face blue or green). Fortunately, you can take a pill that will cure you. It has no effect if you are healthy, but if you have one of these two diseases and you take the wrong pill, you die. Imagine that, in each case, the color your face turns is consistent with the disease 75% of the time, and that the green disease is five times more common than the blue disease. What color pill do you take?

Most people’s hunch (and the hunch shared by medical professionals whom Amos asked) is that they should take the blue pill because (a) their face is blue, and (b) the color their face turns is consistent most of the time, 75%. But this ignores the base rates of the disease.

We fill in a fourfold table. We aren’t told the size of the population we’re dealing with, so to facilitate the construction of the table, let’s assume a population of 120 (that’s the number that goes in the lower right area outside the table). From the problem, we have enough information to fill in the rest of the table.

If the green disease is five times more common than the blue disease, that means that out of 120 people who have one or the other, 100 must have the green disease and 20 must have the blue disease.

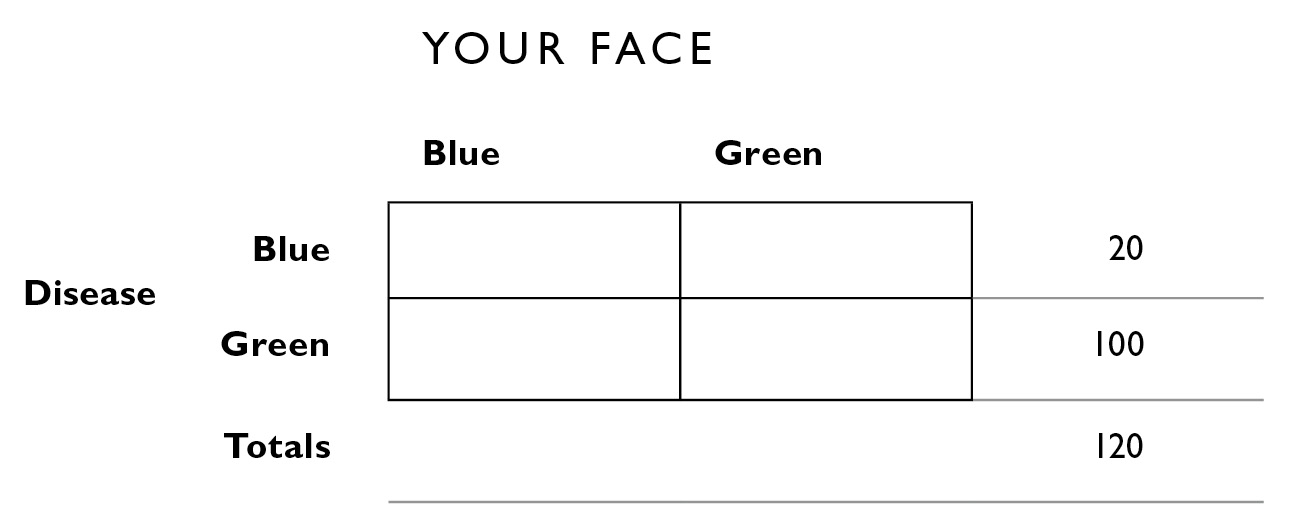
Because the color of your face is consistent with the disease 75% of the time, 75% of the people with blue disease have a blue face; 75% of 20 = 15. The rest of the table is filled in similarly.

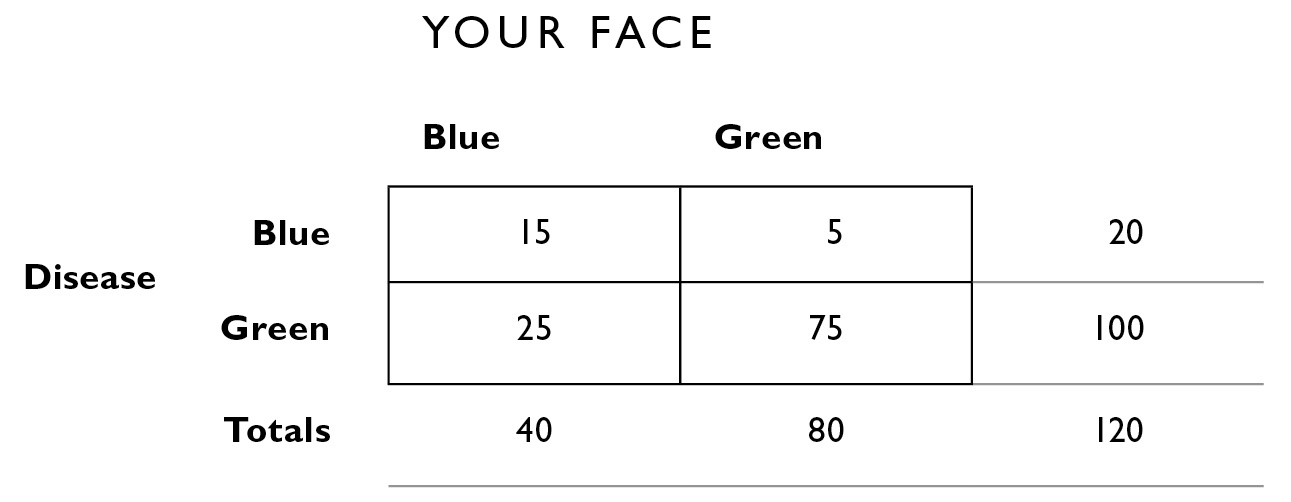
Now, before you take the blue pill—which could either cure or kill you—the Bayesian question you need to ask is “What is the probability that I have the blue disease, given that I have a blue face?” The answer is that out of the 40 people who have a blue face, 15 of them have the disease: 15/40 = 38%. The probability that you have the green disease, given that you have a blue face, is 25/40, or 62%. You’re much better off taking the green pill regardless of what color your face is. This is because the green face disease is far more common than the blue face disease. Again, we are pitting base rates against symptoms, and we learned that base rates should not be ignored. It is difficult to do this in our heads—the fourfold table gives a way of organizing the information visually that is easy to follow. Calculations like this are why doctors will often start patients on a course of antibiotics before they receive test results to know exactly what is wrong—certain antibiotics work against enough common diseases to warrant them.

In the example of blurritis that I began with, 201 people will test positive for a disease that only 1 person has. In many actual health-care scenarios, all 201 people will be given medication. This illustrates another important concept in medical practice: the number needed to treat. This is the number of people who have to take a treatment, such as a medication or surgery, before one person can be cured. A number needed to treat of 201 is not unusual in medicine today. There are some routinely performed surgeries where the number needed to treat is 48, and for some drugs, the number can exceed 300.

Blue faces and tests for imaginary diseases aside, what about the decisions that confront one’s mortality directly? Your doctor says these meds will give you a 40% chance of living an extra five years. How do you evaluate that?

There is a way to think about this decision with the same clear rationality that we applied to the two-poison problem, using the concept of “expected value.” The expected value of an event is its probability multiplied by the value of the outcome. Business executives routinely evaluate financial decisions with this method. Suppose someone walks up to you at a party and offers to play a game with you. She’ll flip a fair coin, and you get $1 every time it comes up heads. How much would you pay to play this game? (Assume for the moment that you don’t particularly enjoy the game, though you don’t particularly mind it—what you’re interested in is making money.) The expected value of the game is 50 cents, that is, the probability of the coin coming up heads (.5) times the payoff ($1). Note that the expected value is often not an amount that you can actually win in any one game: Here you either win $0 or you win $1. But over many hundreds of repetitions of the game, you should have earned close to 50 cents per game. If you pay less than 50 cents per game to play, in the long run you’ll come out ahead.

Expected values can also be applied to losses. Suppose you’re trying to figure out whether to pay for parking downtown or take the chance of getting a ticket by parking in a loading zone. Imagine that the parking lot charges $20 and that the parking ticket is $50, but you know from experience that there’s only a 25% chance you’ll get a ticket. Then the expected value of going to the parking lot is -$20: You have a 100% chance of having to pay the attendant $20 (I used a minus sign to indicate that it’s a loss).

The decision looks like this:

a. Pay for parking: A 100% chance of losing $20

b. Don’t pay for parking: A 25% chance of losing $50

The expected value of the parking ticket is 25% × -$50, which is -$12.50. Now of course you hate parking tickets and you want to avoid them. You might be feeling unlucky today and want to avoid taking chances. So today you might pay the $20 for parking in order to avoid the possibility of being stuck with a $50 ticket. But the rational way to evaluate the decision is to consider the long term. We’re faced with hundreds of decisions just like this in the course of our daily lives. What really matters is how we’re going to make out on average. The expected value for this particular decision is that you will come out ahead in the long run by paying parking tickets: a loss of $12.50 on average versus a loss of $20. Over a year of parking once a week on this particular street, you’ll spend $650 on parking tickets versus $1,040 on parking lots—a big difference. Of course, on any particular day, you can apply Bayesian updating. If you see a meter reader inching along the street toward your parking spot in the loading zone, that’s a good day to go to the parking lot.

Expected value also can be applied to nonmonetary outcomes. If two medical procedures are identical in their effectiveness and long-term benefits, you might choose between them based on how much time they’ll take out of your daily routine.

Procedure 1: A 50% chance of requiring 6 weeks of recovery and a 50% chance of requiring only 2 weeks

Procedure 2: A 10% chance of requiring 12 weeks and a 90% chance of requiring only 0.5 weeks

Again I use a minus sign to indicate the loss of time. The expected value (in time) of procedure 1 is therefore

(.5 × -6 weeks) + (.5 × -2 weeks) = -3 + -1 = -4 weeks.

The expected value of procedure 2 is

(.1 × -12) + (.9 × -.5) = -1.2 + -.45 = -1.65 weeks.

Ignoring all other factors, you’re better off with procedure 2, which will have you out of commission for only about a week and a half (on average), versus procedure 1, which will have you out for 4 weeks (on average).

Of course you may not be able to ignore all other factors; minimizing the amount of recovery time may not be your only concern. If you’ve just booked nonrefundable tickets on an African safari that leaves in 11 weeks, you can’t take the chance of a 12-week recovery. Procedure 1 is better because the worst-case scenario is you’re stuck in bed for 6 weeks. So expected value is good for evaluating averages, but it is often necessary to consider best- and worst-case scenarios. The ultimate extenuating circumstance is when one of the procedures carries with it a risk of fatality or serious disability. Expected value can help organize this information as well.

Risks Either Way

At some point in your life, it is likely you’ll be called upon to make critical decisions about your health care or that of someone you care about. Adding to the difficulty is that the situation is likely to cause physical and psychological stress, reducing the sharpness of your decision-making abilities. If you ask your doctor for the accuracy of the test, he may not know. If you try to research the odds associated with different treatments, you may find that your doctor is ill-equipped to walk through the statistics. Doctors are clearly essential in diagnosing an illness, in laying out the different treatment options, treating the patient, and following up to make sure the treatment is effective. Nevertheless, as one MD put it, “Doctors generate better knowledge of efficacy than of risk, and this skews decision-making.” Moreover, research studies focus on whether or not an intervention provides a cure, and the issue of side effects is less interesting to those who have designed the studies. Doctors educate themselves about the success of procedures but not so much the drawbacks—this is left to you to do, another form of shadow work.

Take cardiac bypass surgery—there are 500,000 performed in the United States every year. What is the evidence that it is helpful? Randomized clinical trials show no survival benefit in most patients who had undergone the surgery. But surgeons were unconvinced because the logic of the procedure to them was justification enough. “You have a plugged vessel, you bypass the plug, you fix the problem, end of story.” If doctors think a treatment should work, they come to believe that it does work, even when the clinical evidence isn’t there.

Angioplasty went from zero to 100,000 procedures a year with no clinical trials—like bypass surgery, its popularity was based simply on the logic of the procedure, but clinical trials show no survival benefit. Some doctors tell their patients that angioplasty will extend their life expectancy by ten years, but for those with stable coronary disease, it has not been shown to extend life expectancy by even one day.

Were all these patients stupid? Not at all. But they were vulnerable. When a doctor says, “You have a disease that could kill you, but I have a treatment that works,” it is natural to jump at the chance. We ask questions, but not too many—we want our lives back, and we’re willing to follow the doctor’s orders. There is a tendency to shut down our own decision-making processes when we feel overwhelmed, something that has been documented experimentally. People given a choice along with the opinion of an expert stop using the parts of the brain that control independent decision-making and hand over their decision to the expert.

On the other hand, life expectancy isn’t the whole story, even though this is the way many cardiologists sell the bypass and angioplasty to their patients. Many patients report dramatically improved quality of life after these procedures, the ability to do things they love. They may not live longer, but they live better. This is a crucial factor in any medical choice, one that should not be swept under the rug. Ask your doctor not just about efficacy and mortality, but quality of life and side effects that may impact it. Indeed, many patients value quality of life more than longevity and are willing to trade one for the other.

A potent example of the pitfalls in medical decision-making comes from the current state of prostate cancer treatments. An estimated 2.5 million men in the United States have prostate cancer, and 3% of men will die from it. That doesn’t rank it in the Top Ten causes of death, but it is the second leading cause of cancer death for men, after lung cancer. Nearly every urologist who delivers the news will recommend radical surgery to remove the prostate. And on first blush, it sounds reasonable—we see cancer, we cut it out.

Several things make thinking about prostate cancer complicated. For one, it is a particularly slow-progressing cancer—most men die with it rather than of it. Nevertheless, the C-word is so intimidating and frightening that many men just want to “cut it out and be done with it.” They are willing to put up with the side effects to know that the cancer is gone. But wait, there is a fairly high incidence of recurrence following surgery. And what about the side effects? The incident rate—how often side effects occur among patients after surgery—are in parentheses :

• inability to maintain an erection sufficient for intercourse (80%)
• shortening of the penis by one inch (50%)
• urinary incontinence (35%)
• fecal incontinence (25%)
• hernia (17%)
• severing of urethra (6%)

The side effects are awful. Most people would say they’re better than death, which is what they think is the alternative to surgery. But the numbers tell a different story. First, because prostate cancer is slow moving and doesn’t even cause symptoms in most of the people who have it, it can safely be left untreated in some men. How many men? Forty-seven out of 48. Put another way, for every 48 prostate surgeries performed, only one life is extended—the other 47 patients would have lived just as long anyway, and not had to suffer the side effects. Thus, the number needed to treat to get one cure is 48. Now, as to the side effects, there’s over a 97% chance a patient will experience at least one of those listed above. If we ignore the sexual side effects—the first two—and look only at the others, there is still more than a 50% chance that the patient will experience at least one of them, and a pretty big chance he’ll experience two. So, of the 47 people who were not helped by the surgery, roughly 24 are going to have at least one side effect. To recap: For every 48 prostate surgeries performed, 24 people who would have been fine without surgery experience a major side effect, while 1 person is cured. You are 24 times more likely to be harmed by the side effect than helped by the cure. Of men who undergo the surgery, 20% regret their decision. Clearly, it is important to factor quality of life into the decision.

So why, then, does nearly every urologist recommend the surgery? For one, the surgery is one of the most complicated and difficult surgeries known. You might think this is a good reason for them not to recommend it, but the fact is that they have an enormous amount invested in learning to do it. The training required is extensive, and those who have mastered it are valued for this rare skill. In addition, patients and their families carry expectations that a physician will do something. Patients tend to be dissatisfied with a practitioner who says, “We’ll keep an eye on it.” People who go to an internist with a cold are measurably unhappy if they walk out of the office empty-handed, without a prescription. Multiple studies show that these patients feel their doctor didn’t take them seriously, wasn’t thorough, or both.

Another reason surgery is pushed is that the surgeon’s goal is to eradicate the cancer and to do so with the lowest possible incidence of recurrence. Patients are complicit in this: “It’s very hard to tell a surgeon ‘I’d like to leave a cancer in place,’” explains Dr. Jonathan Simons, president of the Prostate Cancer Foundation. Medical schools teach that surgeries are the gold standard for most cancers, with survival rates higher than other methods, and much higher than ignoring the problem. They use a summary statistic of how many people die of the cancer they were treated for, five and ten years after surgery. But this summary ignores important data such as susceptibility to other maladies, quality of life after surgery, and recovery time.

Dr. Barney Kenet, a Manhattan dermatologist, finds all this fascinating. “Surgeons are taught that ‘a chance to cut is a chance to cure,’” he says. “It’s part of the DNA of their culture. In the examples you’ve been giving me about cancer, with the odds and statistics all carefully analyzed, the science of treatment is in collision with the art of practicing medicine—and it is an art.”

Medical schools and surgeons may not worry so much about quality of life, but you should. Much of medical decision-making revolves around your own willingness to take risks, and your threshold for putting up with inconveniences, pain, or side effects. How much of your time are you willing to spend driving to and from medical appointments, sitting in doctors’ offices, fretting about results? There are no easy answers, but statistics can go a long way toward clarifying the issues here. To return to prostate surgeries, the advised recovery period is six weeks. That doesn’t seem like an unreasonable amount of time, considering that the surgery can save your life.

But the question to ask is not “Am I willing to invest six weeks to save my life?” but rather “Is my life actually being saved? Am I one of the forty-seven people who don’t need the surgery or am I the one who does?” Although the answer to that is unknowable, it makes sense to rely on the probabilities to guide your decision; it is statistically unlikely that you will be helped by the surgery unless you have specific information that your cancer is aggressive. Here’s an additional piece of information that may bring the decision into sharp focus: The surgery extends one’s life, on average, by only six weeks. This number is derived from the average of the forty-seven people whose lives were not extended at all (some were even shortened by complications from the surgery) and the one person whose life was saved by the surgery and has gained five and a half years. The six-week life extension in this case exactly equals the six-week recovery period! The decision, then, can be framed in this way: Do you want to spend those six weeks now, while you’re younger and healthier, lying in bed recovering from a surgery you probably didn’t need? Or would you rather take the six weeks off the end of your life when you’re old and less active?

Many surgical procedures and medication regimens pose just this trade-off: The amount of time in recovery can equal or exceed the amount of life you’re saving. The evidence about the life-extending benefits of exercise is similar. Don’t get me wrong—exercise has many benefits, including mood enhancement, strengthening of the immune system, and improving muscle tone (and hence overall appearance). Some studies show that it even improves clarity of thought through oxygenation of the blood. But let’s examine one claim that has received a lot of attention in the news, that if you perform aerobic exercise an hour a day and reach your target heart rate, you will extend your life. Sounds good, but by how much? Some studies show you extend your life by one hour for every hour you exercise. If you love exercise, this is a great deal—you’re doing something you love and it’s extending your life by the same amount. This would be like saying that for every hour you have sex, or every hour you eat ice cream, you’ll live an extra hour. Easy choice—the hour you spend on the activity is essentially “free” and doesn’t count against the number of hours you’ve been allotted in this life. But if you hate exercise and find it unpleasant, the hour you’re spending amounts to an hour lost. There are enormous benefits to daily exercise, but extending your life is not one of them. That’s no reason not to exercise—but it’s important to have reasonable expectations for the outcome.

Two objections to this line of thinking are often posed. The first is that talking about averages in a life-or-death decision like this doesn’t make sense because no actual prostate surgery patient has their life extended by the average quoted above of six weeks. One person has his life extended by five and a half years, and forty-seven have their lives extended by nothing at all. This “average” life extension of six weeks is simply a statistical fiction, like the parking example.

It is true, no one person gains by this amount; the average is often a number that doesn’t match a single person. But that doesn’t invalidate the reasoning behind it. Which leads to the second objection: “You can’t evaluate this decision the way you evaluate coin tosses and card games, based on probabilities. Probabilities and expected values are only meaningful when you are looking at many, many trials and many outcomes.” But the rational way to view such decisions is to consider these offers not as “one-offs,” completely separated from time and life experience, but as part of a string of decisions that you will need to make throughout your life. Although each individual decision may be unique, we are confronted with a lifetime of propositions, each one carrying a probability and an expected value. You are not making a decision about that surgical procedure in isolation from other decisions in your life. You are making it in the context of thousands of decisions you make, such as whether to take vitamins, to exercise, to floss after every meal, to get a flu shot, to get a biopsy. Strictly rational decision-making dictates that we pay attention to the expected value of each decision.

Each decision carries uncertainty and risks, often trading-off time and convenience now for some unknown outcome later. Of course if you were one hundred percent convinced that you’d enjoy perfect oral health if you flossed after every meal, you would do so. Do you expect to get that much value from flossing so often? Most of us aren’t convinced, and flossing three times a day (plus more for snacks) seems, well, like more trouble than it’s worth.

Obtaining accurate statistics may sound easy but often isn’t. Take biopsies, which are commonplace and routinely performed, and carry risks that are poorly understood even by many of the surgeons who perform them. In a biopsy, a small needle is inserted into tissue, and a sample of that tissue is withdrawn for later analysis by a pathologist who looks to see if the cells are cancerous or not. The procedure itself is not an exact science—it’s not like on CSI where a technician puts a sample in a computer and gets an answer out the other end.

The biopsy analysis involves human judgment and what amounts to a “Does it look funny?” test. The pathologist or histologist examines the sample under a microscope and notes any regions of the sample that, in her judgment, are not normal. She then counts the number of regions and considers them as a proportion of the entire sample. The pathology report may say something like “5% of the sample had abnormal cells” or “carcinoma noted in 50% of the sample.” Two pathologists often disagree about the analysis and even assign different grades of cancer for the same sample. That’s why it’s important to get a second opinion on your biopsy—you don’t want to start planning for surgery, chemotherapy, or radiation treatment until you’re really sure you need it. Nor do you want to grow too complacent about a negative biopsy report.

To stick with the prostate cancer example, I spoke with six surgeons at major university teaching hospitals and asked them about the risks of side effects from prostate biopsy. Five of them said the risk of side effects from the biopsy was around 5%, the same as what you can read for yourself in the medical journals. The sixth said there was no risk—that’s right, none at all. The most common side effect mentioned in the literature is sepsis; the second most common is a torn rectum; and the third is incontinence. Sepsis is dangerous and can be fatal. The biopsy needle has to pass through the rectum, and the risk of sepsis comes from contamination of the prostate and abdominal cavity with fecal material. The risk is typically reduced by having the patient take antibiotics prior to the procedure, but even with this precaution, there still remains a 5% risk of an unwanted side effect.

None of the physicians I spoke to chose to mention a recovery period for the biopsy, or what they euphemistically refer to as side effects of “inconvenience.” These are not health-threatening, simply unpleasant. It was only when I brought up a 2008 study in the journal Urology that they admitted that one month after biopsy, 41% of men experienced erectile dysfunction, and six months later, 15% did. Other side effects of “inconvenience” include diarrhea, hemorrhoids, gastrointestinal distress, and blood in the semen that can last for several months. Two of the physicians sheepishly admitted that they deliberately withhold this information. As one put it, “We don’t mention these complications to patients because they might be discouraged from getting the biopsy, which is a very important procedure for them to have.” This is the kind of paternalism that many of us dislike from doctors, and it also violates the core principle of informed consent.

Now, that 5% risk of serious side effects may not sound so bad, but consider this: Many men who have been diagnosed with early-stage or low-grade prostate cancer are choosing to live with the cancer and to monitor it, a plan known as watchful waiting or active surveillance. In active surveillance, the urologist may call for biopsies at regular intervals, perhaps every twelve to twenty-four months. For a slow-moving disease that may not show any symptoms for over a decade, this means that some patients will undergo five or more biopsies. What is the risk of sepsis or another serious side effect during one or more biopsies if you have five biopsies, each one carrying a risk of 5%?

This calculation doesn’t follow the multiplication rule I outlined above; we’d use that if we wanted to know the probability of a side effect on all five biopsies—like getting heads on a coin five times in a row. And it doesn’t require a fourfold table because we’re not asking a Bayesian question such as “What is the probability I have cancer, given that the biopsy was positive?” (Pathologists sometimes make mistakes—this is equivalent to the diagnosticity of the blood tests we saw earlier.) To ask about the risk of a side effect in at least one out of five biopsies—or to ask about the probability of getting at least one head on five tosses of a coin—we need to use something called the binomial theorem. The binomial can tell you the probability of the bad event happening at least one time, all five times, or any number you like. If you think about it, the most useful statistic in a case like this is not the probability of your having an adverse side effect exactly one time out of your five biopsies (and besides, we already know how to calculate this, using the multiplication rule). Rather, you want to know the probability of having an adverse side effect at least one time, that is, on one or more of the biopsies. These probabilities are different.

The easiest thing to do here is to use one of the many available online calculators, such as this one: http://www.stat.tamu.edu/~west/applets/binomialdemo.html.

To use it, you enter the following information into the onscreen boxes:

n refers to the number of times you are undergoing a procedure (in the language of statistics, these are “trials”).

p refers to the probability of a side effect (in the language of statistics, these are “events”).

X refers to how many times the event occurs.

Using the example above, we are interested in knowing the probability of having at least one bad outcome (the event) if you undergo the biopsy five times. Therefore,

n = 5 (5 biopsies)

p = 5%, or .05

X = 1 (1 bad outcome)

Plugging these numbers into the binomial calculator, we find that if you have five biopsies, the probability of having a side effect at least once is 23%.

Of the five surgeons who acknowledged that there was a 5% risk of side effects from the prostate biopsy, only one understood that the risk increased with each biopsy. Three of them said that the 5% risk applied to a lifetime of having biopsies—you could have as many as you want, and the risk never increased.

I explained that each biopsy represented an independent event, and that two biopsies presented a greater risk than one. None of them were buying it. The first of my conversations went like this:

“I read that the risk of serious complications from the biopsy is five percent.”

“That’s right.”

“So if a patient has biopsies five times, that increases their risk to nearly twenty-five percent.”

“You can’t just add the probabilities together.”

“I agree, you can’t. You need to use the binomial theorem, and you come up with twenty-three percent—very close to twenty-five percent.”

“I’ve never heard of the binomial theorem and I’m sure it doesn’t apply here. I don’t expect you to understand this. It requires statistical training.”

“Well, I’ve had some statistical training. I think I can understand.”

“What is it you do for a living again?”

“I’m a research scientist—a neuroscientist. I lecture in our graduate statistics courses and I’ve published some statistical methods papers.”

“But you’re not an MD like I am. The problem with you is that you don’t understand medicine. You see, medical statistics are different from other statistics.”

“What?”

“I’ve had twenty years of experience in medicine. How much have you had? I’m dealing in the real world. You can have all the theories you want, but you don’t know anything. I see patients every day. I know what I’m seeing.”

Another surgeon, a world expert in the da Vinci “robot” guided surgery, told me, “These statistics don’t sound right. I’ve probably done five hundred biopsies and I don’t think I’ve seen more than a couple of dozen cases of sepsis in my whole career.”

“Well, twenty-four out of five hundred is about five percent.”

“Oh. Well, I’m sure it wasn’t that many, then. I would have noticed if it was five percent.”

Either a glutton for punishment, or an optimist, I visited the department head for oncology at another leading hospital. If a person had prostate cancer, I pointed out, they’re better off not having surgery because of the number needed to treat: Only 2% of patients are going to benefit from the surgery.

“Suppose it was you with the diagnosis,” he said. “You wouldn’t want to forgo the surgery! What if you’re in that two percent?”

“Well . . . I probably wouldn’t be.”

“But you don’t know that.”

“You’re right, I don’t know it, but by definition, it is unlikely—there’s only a two percent chance that I’d be in the two percent.”

“But you wouldn’t know that you’re not. What if you were? Then you’d want the surgery. What’s the matter with you?”

I discussed all this with the head of urological oncology at yet another university teaching hospital, a researcher-clinician who publishes studies on prostate cancer in scientific journals and whose papers had an expert’s command of statistics. He seemed disappointed, if unsurprised, at the stories about his colleagues. He explained that part of the problem with prostate cancer is that the commonly used test for it, the PSA, is poorly understood and the data are inconsistent as to its effectiveness in predicting outcomes. Biopsies are also problematic because they rely on sampling from the prostate, and some regions are easier to sample from than others. Finally, he explained, medical imaging is a promising avenue—magnetic resonance imaging and ultrasound for example—but there have been too few long-term studies to conclude anything about their effectiveness at predicting outcomes. In some cases, even high-resolution MRIs miss two-thirds of the cancers that show up in biopsies. Nevertheless, biopsies for diagnosis, and surgery or radiation for treatment, are still considered the gold standards for managing prostate cancer. Doctors are trained to treat patients and to use effective techniques, but they are not typically trained in scientific or probabilistic thinking—you have to apply these kinds of reasoning yourself, ideally in a partnership with your physician.

What Doctors Offer

But wait a minute—if MDs are so bad at reasoning, how is it that medicine relieves so much suffering and extends so many lives? I have focused on some high-profile cases—prostate cancer, cardiac procedures—where medicine is in a state of flux. And I’ve focused on the kinds of problems that are famously difficult, that exploit cognitive weaknesses. But there are many successes: immunization, treatment of infection, organ transplants, preventive care, and neurosurgery (like Salvatore Iaconesi’s, in Chapter 4), to name just a few.

The fact is that if you have something wrong with you, you don’t go running to a statistics book, you go to a doctor. Practicing medicine is both an art and a science. Some doctors apply Bayesian inferencing without really knowing they’re doing it. They use their training and powers of observation to engage in pattern matching—knowing when a patient matches a particular pattern of symptoms and risk factors to inform a diagnosis and prognosis.

As Scott Grafton, a top neurologist at UC Santa Barbara, says, “Experience and implicit knowledge really matter. I recently did clinical rounds with two emergency room doctors who had fifty years of clinical experience between them. There was zero verbal gymnastics or formal logic of the kind that Kahneman and Tversky tout. They just recognize a problem. They have gained skill through extreme reinforcement learning, they become exceptional pattern recognition systems. This application of pattern recognition is easy to understand in a radiologist looking at X-rays. But it is also true of any great clinician. They can generate extremely accurate Bayesian probabilities based on years of experience, combined with good use of tests, a physical exam, and a patient history.” A good doctor will have been exposed to thousands of cases that form a rich statistical history (Bayesians call this a prior distribution) on which they can construct a belief around a new patient. A great doctor will apply all of this effortlessly and come to a conclusion that will result in the best treatment for the patient.

“The problem with Bayes and heuristics arguments,” Grafton continues, “is they fail to recognize that much of what physicians learn to do is to extract information from the patient directly, and to individualize decision-making from this. It is extremely effective. A good doctor can walk into a hospital room and smell impending death.” When many doctors walk into an ICU room, for example, they look at the vital signs and the chart. When Grafton walks into an ICU room, he looks at the patient, leveraging his essential human capacity to understand another person’s mental and physical state.

Good doctors talk to their patients to understand the history and symptoms. They elegantly use pattern matching. The science informs their judgments, but they don’t rely on any one test. In the two-poison and optical blurritis stories, I’ve glossed over an important fact about how real medical decisions are made. Your doctor wouldn’t have ordered the test unless he thought, based on his examination of you and your history, that you might have the disease. For my made-up blurritis, although the base rate in the general population is 1 in 38,000, that’s not the base rate of the disease for people who have blurry vision, end up in a doctor’s office and end up taking the test. If that base rate is, say, 1 in 9,500, you can redo the table and find out that the chance of your having blurritis drops from 1 in 201 to about 1 in 20. This is what Bayesian updating is all about—finding statistics that are relevant to your particular circumstance and using them. You improve your estimates of the probability by constraining the problem to a set of people who more closely resemble you along pertinent dimensions. The question isn’t “What is the probability that I’ll have a stroke?” for example, but “What is the probability that someone my age, gender, blood pressure, and cholesterol level will have a stroke.” This involves combining the science of medicine with the art of medicine.

And although there are things that medicine is not particularly good at, it is hard to argue with the overwhelming successes of medicine over the past hundred years. The U.S. Centers for Disease Control and Prevention (CDC) in Atlanta reports nearly complete eradication—a 99% decrease in morbidity—between 1900 and 1998 for nine diseases that formerly killed hundreds of thousands of Americans: smallpox, diphtheria, tetanus, measles, mumps, rubella, Haemophilus influenzae, pertussis, and polio. Diphtheria fell from 175,000 cases to one, measles from 500,000 to about 90. For most of human history, from around 10,000 BCE to 1820, our life expectancy was capped at about twenty-five years. World life expectancy since then has increased to more than sixty years, and since 1979, U.S. life expectancy has risen from seventy-one to seventy-nine.

What about cases where doctors are more directly involved with patients? After all, life span may be attributable to other factors, such as improved hygiene. In the battlefield, even while weapons have become more damaging, a soldier’s odds of being successfully treated for a wound have increased dramatically: Through the Civil War and both world wars, the odds of dying from a wound were around 1 in 2.5; during the Iraq War, they had fallen to 1 in 8.2. Infant, neonatal, and postneonatal mortality rates have all been reduced. In 1915, for every 1,000 births, 100 infants would die before their first birthday; in 2011, that number had dropped to 15. And although prostate cancer, breast cancer, and pancreatic cancer have been particularly challenging to manage, survival rates for childhood leukemia have risen from near 0% in 1950 to 80% today.

Clearly, medicine is doing a lot right, and so is the science behind it. But there remains a gray, shadowy area of pseudomedicine that is problematic because it clouds the judgment of people who need real medical treatment and because the area is, well, disorganized.

Alternative Medicine: A Violation of Informed Consent

One of the core principles of modern medicine is informed consent—that you have been fully briefed on all the pros and cons of any treatment you submit to, that you have been given all of the information available in order to make an informed decision.

Unfortunately, informed consent is not truly practiced in modern health care. We are bombarded with information, most of it incomplete, biased, or equivocal, and at a time when we are least emotionally prepared to deal with it. This is especially true with alternative medicine and alternative therapies.

An increasing number of individuals seek alternatives to the professional medical-hospital system for treating illness. Because the industry is unregulated, figures are hard to come by, but The Economist estimates that it is a $60 billion business worldwide. Forty percent of Americans report using alternative medicines and therapies; these include herbal and homeopathic preparations, spiritual or psychic healing practices, and various nonmedical manipulations of body and mind with a healing intent. Given its prominence in our lives, there is some basic information anyone consenting to this kind of health care should have.

Alternative medicine is simply medicine for which there is no evidence of effectiveness. Once a treatment has been scientifically shown to be effective, it is no longer called alternative—it is simply called medicine. Before a treatment becomes part of conventional medicine, it undergoes a series of rigorous, controlled experiments to obtain evidence that it is both safe and effective. To be considered alternative medicine, nothing of the kind is required. If someone holds a belief that a particular intervention works, it becomes “alternative.” Informed consent means that we should be given information about a treatment’s efficacy and any potential hazards, and this is what is missing from alternative medicine.

To be fair, saying that there is no evidence does not mean that the treatment is ineffective; it simply means its effectiveness has not yet been demonstrated—we are agnostic. But the very name “alternative medicine” is misleading. It is alternative but it is not medicine (which begs the question What is it an alternative to?).

How is science different from pseudoscience? Pseudoscience often uses the terminology of science and observation but does not use the full rigor of controlled experiments and falsifiable hypotheses. A good example is homeopathic medicine, a nineteenth-century practice that entails giving extremely small doses (or actually no dose at all) of harmful substances that are claimed to provide a cure. It is based on two beliefs. First is that when a person shows symptoms such as insomnia, stomach distress, fever, cough, or tremors, administering a substance which, in normal doses, causes those symptoms, can cure it. There is no scientific basis for that claim. If you have poison ivy, and I give you more poison ivy, all I’ve done is given you more poison ivy. It is not a cure—it is the problem! The second belief is that diluting a substance repeatedly can leave remnants of the original substance that are active and have curative properties, and that the more dilute the substance is, the more effective or powerful it is. According to homeopaths, the “vibrations” of the original substance leave their imprint on water molecules.

And the dilution has to be accomplished according to a very specific procedure. A homeopathic technician takes one part of the chemical substance and dilutes it in ten parts of water, then shakes it up and down ten times, back and forth ten times, and from side to side ten times. Then he takes one part of that solution and dilutes it in ten parts of water, and performs the shaking routine again. He does this at least twenty times altogether, resulting in a solution in which there is one part of the original substance for 100,000,000,000,000,000,000 parts of water. For retail homeopathic products, dilutions are routinely 1 followed by 30 zeros, and often 1 followed by—get this—1,500 zeros. This is equivalent to taking one grain of rice, crushing it into a powder, and dissolving it in a sphere of water the size of our solar system. Oh, I forgot: and then repeating that process twenty-six times. Homeopathy was invented before the Italian scientist Amedeo Avogadro discovered a mathematical constant that now bears his name, expressing the number of atoms or molecules that are retained in dilutions (6.02 × 10²³). The point is that in standard, retail homeopathic dilutions, there is nothing remaining of the original substance. But that’s supposed to be good because, remember, the more dilute the homeopathic medicine is, the stronger it is. All this has led professional skeptic James Randi to the observation that the way to overdose on homeopathic medicine is to not take any at all. (Randi has offered $1 million for more than a decade to anyone who can provide evidence that homeopathy works.)

Homeopathy is pseudoscience because (a) it doesn’t stand up to controlled experiments, (b) it uses the language of science such as dilution and molecule, and (c) it makes no sense within a scientific understanding of cause and effect.

Setting homeopathy aside, when it comes to serious illness, such as cancer, infection, Parkinson’s disease, pneumonia, or even milder illnesses like common colds and flu, there is no evidence that alternative medicine is effective. Edzard Ernst, a British research scientist, reviewed hundreds of studies and found that 95% of the treatments were indistinguishable from no treatment at all—equivalent to placebo. (The other 5%, which do work, may represent experimental error, according to traditional thresholds for success in scientific research.) Vitamins and supplements fare no better. After extensive clinical trials spanning decades and many different research labs and protocols, it’s been found that multivitamins are not effective for anything at all. In fact, vitamins can harm. In the doses contained in vitamin pills, Vitamin E and folic acid are associated with increased risk for cancer. Excess Vitamin D is associated with an increased risk for cardiac inflammation, and excess Vitamin B6 is associated with nerve damage. In dietary amounts—what you get from a normal diet as opposed to taking supplements—these vitamins are not a problem, but the amounts typically found in supplements and over-the-counter vitamin pills can be harmful. And in spite of the fact that millions of Americans take Vitamin C or echinacea when they feel a cold coming on, there is little evidence that these help. Why do we think they do?

Our forebrains have evolved to notice co-occurrences of events, but not a lack of occurrences. This relates to the fourfold tables we looked at earlier: Our brains are biased to focus on what’s in the upper left square—psychologists call this illusory correlation.

The reason the correlations are illusory is that the upper left square doesn’t tell us all we need to know to draw the best conclusion. Imagine you feel a cold coming on so you start taking lots of echinacea. You notice that the cold never develops. This happens to you at five different times and so you conclude that the echinacea has helped. Your fourfold table looks like this:

Pretty impressive! Here are some problems. A certain number of colds are going to go away if you do nothing. And there might be times when you felt a cold coming on, did nothing, and promptly forgot about it. If you were part of a scientific study, there would be more meticulous data collection than most of us do by ourselves. Here is what the rest of the table might look like if you filled it in as part of a study:

Note that in order to have a complete picture, you need to know on how many days you did not take echinacea and you did not get a cold—that’s most of the time! Needing to know this seems counterintuitive—but that’s the whole point here, that our forebrains have a hard time making sense of this kind of information. Just looking at the table, you can see that a cold is twice as likely to develop if you take echinacea as not (the right column of the table). To put this into Bayesian form, the probability of getting a cold, given that you took echinacea, still equals .67.

By the way, the placebo effect—that we feel better and often get better just from taking something, even if it has no medicinal ingredients—is very real and very strong. Larger pills have a bigger placebo effect than small pills. Sham injections have a larger effect than pills. A great deal of the effect of products with no known medicinal value may simply be this placebo effect. This is why double-blind, randomized clinical control trials are necessary: Everyone in the study gets a pill and nobody knows who got what. Many of the people taking the “empty” pill are going to improve relative to people who got nothing, but if the medicine really works, it should work even better than placebo. This is how new treatments are approved.

It’s not just echinacea and Vitamin C that wreak havoc with our causal reasoning. We fall prey to illusory correlations all the time. Have you ever had the experience that you were thinking of someone, someone you hadn’t thought of in a long time, and then suddenly the phone rings and—wow! There they are! Before jumping to the conclusion that psychic powers are involved, you’d need to know three other pieces of information: How often do you think of people who don’t call you, how often do you not think of people who do call you, and finally, how often do you not think of someone and then they don’t call! If you work all this out in a fourfold table, it is likely you’ll find that the occasionally vivid coincidences are swamped by events of the other three kinds, making the point that these correlations are illusory.

Our brains evidently have evolved to focus on the upper left cell, the hits, and remember nothing else. One of my former teachers, Paul Slovic, dubbed this denominator neglect. Slovic says we imagine the numerator—the tragic story you saw on the news about a car crash—and don’t think about the denominator—the overwhelming number of automobile trips that end safely. Denominator neglect shows up in very odd ways. In one study, people were told that a disease kills 1,286 people out of every 10,000. They judged this as more dangerous than did people who were told of a disease that kills 24.14% of the population. Note that 1,286/10,000 is just under 13%. So, in reality, it’s only about half as dangerous. But in the first case, we focus on the numerator, the 1,286 individuals who will be stricken with the disease. We may try to picture that many people in hospital beds. In the second case, we hear 24.14% and the brain tends to treat it as an abstract statistic with no human beings attached.

Denominator neglect leads to a tendency to catastrophize, to imagine the worst possible scenario without placing it in proper statistical perspective. As Daniel Kahneman writes, “Every parent who has stayed up waiting for a teenage daughter who is late from a party will recognize the feeling. You may know that there is really (almost) nothing to worry about, but you cannot help images of disaster from coming to mind.”

The vividness with which we can recall catastrophes, coupled with denominator neglect, can lead to truly terrible decisions. In the two months following the terrorist attacks of September 11, 2001, so many people in the United States were afraid to fly that they took to their cars for trips they otherwise would have taken by plane. There were no more airplane crashes in October or November, but 2,170 more people died in automobile crashes during that period than usually do. These people focused on the numerator (four horrible airplane crashes, 246 people aboard them) but not the denominator (ten million safe commercial flights per year in the United States). As one researcher put it, “Terrorists can strike twice—first, by directly killing people, and second, through dangerous behaviors induced by fear in people’s minds.”

Related to this is that we tend to overweight rare events. Kahneman describes this scenario: Imagine that intelligence officers determine that suicide bombers have entered two different cities and are ready to strike. One city has one suicide bomber, the other city has two. Logically, the citizens of the first city should feel twice as safe. But they probably don’t. The image is so vivid that the fear is roughly the same. Now, if there were one hundred suicide bombers, that would be a different story, but the point is that we are not sensitive to the math because our brains weren’t built that way. Fortunately, we can train them.

Which brings us back to alternative medicine and the fact that many of its claims rest on illusory correlations, based on denominator neglect. The appeal of alternative medicine is at least in part because a growing number of people are suspicious of “Western medicine,” and they seek alternatives. Overwhelmed by the imperfections in the way modern health care is managed, they feel a need to rebel against those who have supplied us with imperfectly effective and expensive drugs. They are suspicious of the large profits that pharmaceutical companies (and some hospitals) make, and are wary of treatments that are recommended within a strong culture of maximizing profits—the concern being that some treatments may be prescribed not because they are best for the patient but because they are best for those who stand to gain financially. Unfortunately, recent news stories have shown that this is sometimes true.

Alternative medicine enthusiasts also complain about the paternalistic or arrogant manner of some doctors (“I know what’s right for you and you don’t need to understand it”), exemplified by the urological oncologist I spoke to who became hostile when asked to discuss his statistical reasoning about biopsy. At one of the leading hospitals in the United States, breast cancer patients who undergo radiation treatment aren’t told about the high probability of experiencing painful radiation burns, evidently because the oncologists have decided for the patient that the benefits of the treatment outweigh the pain and discomfort of it. But this violates the principle of informed consent. All patients should be given all the information available so they can decide what they are willing to accept and what they are not.

Another thing to worry about is a lack of calibration among some doctors. In one study, physicians making a prognosis were accurate only 20% of the time. In another study, researchers collected autopsy results of patients who died in the hospital. They then compared these to the diagnosis made by the patients’ physicians while they were still alive. The elegant part of this experiment is that the physicians also reported their confidence in the diagnosis they had given. Looking only at those cases in which the doctors were “completely certain” of the diagnosis, they were wrong for about 40% of their patients. Being wrong about so many diagnoses is understandable and perhaps forgivable, given that medical cases can be very complicated, and what we’ve already seen about the imperfection of tests. But being so overconfident is less understandable, because it means the doctors are not paying attention to outcomes.

The appeal of alternative medicine, then, is that it plays into the genuine feelings of distrust that many people feel for the medical establishment. It offers the perhaps romanticized hope of natural products providing natural, noninvasive cures. The use of alternative medicine often feeds a nativist belief that if something is plant-based or natural, it must be good. (But of course this is false: Think hemlock, castor bean seeds, jasmine berries, and poisonous mushrooms.) An additional problem is that herbal and plant-based medicines are not regulated in the United States or in many other countries. The U.S. Food and Drug Administration (FDA) estimates that basic quality control standards are not adhered to by 70% of the companies. And while quality control is a serious problem, with contaminants and fillers being found present in a large number of samples, the supplements themselves can and do cause harm even when they are not compromised by poor manufacturing. A seventeen-year-old Texas youth, Christopher Herrera, showed up at the emergency room of a Houston hospital in 2012 with his chest, face, and eyes bright yellow, “almost highlighter yellow,” according to Dr. Shreena Patel, the doctor who treated him. He had suffered liver damage after using a green tea extract he’d bought at a nutrition store as a fat-burning supplement, and the damage was so severe that he required a liver transplant. Dietary supplements now account for 20% of drug-related liver injuries, tripling the rate from ten years ago.

Yet most of us know someone who claims to have been cured by some form of alternative medicine, whether for a cold, backache, or even cancer. A dear friend of mine was diagnosed with prostate cancer and was told he had six months to live. “Get your affairs in order and do something you’ve always wanted to do,” they said. “A vacation in Hawaii, perhaps.” He told them, “What I’ve always wanted to do is live a long life,” and he walked out.

My friend heard about a doctor specializing in alternative medicine. The doctor did extensive “alternative” blood tests and as a result prescribed a very specific diet and exercise. The list of permitted and forbidden foods was so restrictive, it would take my friend three or four hours a day just to prepare his meals. He followed the diet and exercise program with the same kind of commitment and focus he had applied to every aspect of his life, the kind of discipline that had led him to become the president of a well-known international company when he was only thirty-eight years old.

The six-month death sentence was given twelve years ago. My friend is thriving, doing better than ever before. He went back to his dream-team oncologists two years after they had said he’d be dead and they ran a battery of tests. His PSA was down to nearly zero and his other biomarkers were all normal and stable. They refused to believe he had cured himself with diet and exercise. “There must have been something wrong with our tests when you came in last time” was all they could muster.

I know a half dozen people who have similar stories. They are compelling. I’m grateful that my friends have lived. The important point is that these are not scientific studies, they are just stories. They are uplifting, quizzical, mysterious, challenging stories but just stories. The plural of anecdote is not data. There were no experimental controls, the patients were not randomly assigned to one condition or another, there was no scientist keeping careful records of the progression of either the disease or the cure. We don’t have the opportunity to know what would have happened if my friend hadn’t changed his diet and started exercising—he might have lived just as long and not had to spend eighty hours a month chopping vegetables in his kitchen. Or he might be dead. Not long ago, I asked him if he had gone back for a biopsy or medical imaging to be sure the cancer was really gone. “Why would I do that?” he asked. “I’m healthier than I’ve ever been, I feel great, and it’s not like I would do anything differently based on what they find.”

My friend beating cancer with diet and exercise is neither consistent nor inconsistent with science; it stands outside of scientific scrutiny because the data were not collected in a scientific way.

Like the doctors who were eager to believe in coronary bypass and angioplasties because they had a plausible mechanism, we’re willing to believe that diet and exercise can beat cancer without any scientific support. It’s just plausible enough and it makes intuitive sense to us. None of us has a complete understanding of the relation between diet, exercise, disease, and health. We hear the story and we think, “Yeah, there just might be something to that.” To see that we’re basing this on the plausibility of the mechanism rather than the data, consider that if, instead of diet and exercise, my friend slept upside down in a tent the shape of a pyramid, we’d say that was just crazy.

One of the nice things about science is that it is open to stories like my friend’s so as not to miss out on important new cures. Most scientific findings begin with a simple observation, often serendipitous, that is followed up with careful study; think Newton’s apple or Archimedes displacing the water in his bathtub.

Lying in wait within “alternative medicine” may well be a cure for cancer or other ailments. Research is under way in hundreds of laboratories throughout the world testing herbal preparations, alternative medicines and therapies. But until they are shown to be effective, they carry the danger that they may cause patients to delay seeking treatments that have been shown to work, and consequently delay a cure sometimes beyond the point of no return. This is what happened to Steve Jobs—he rejected surgery to follow an alternative regime of acupuncture, dietary supplements, and juices that he later realized didn’t work and that delayed the conventional treatment that experts say would probably have prolonged his life.

Thousands of people die in the United States every year from diseases that were preventable or curable with “Western medicine.” The scientific method has brought civilization further in the last two hundred years than all other methods over the previous ten thousand years. Medical researchers understand that patients’ lives are at stake in their experiments—often, even before a clinical trial is completed, scientists will see a clear benefit and call off the trial early in order to make the medicine available sooner rather than make patients wait, some of whom are so sick that waiting is not an option.

Indeed, because some of the alternative therapies, such as diet and exercise, do make so much sense, and because there are so very many stories like my friend’s, the U.S. National Institutes of Health (NIH) has set up a division for complementary and alternative medicine to explore such treatments, using all the tools of modern science. So far, the NIH reports many cases of no effects or tiny effects, translating to only small numbers of people who benefit from alternative therapies and an enormous number who don’t. In one typical study, for example, nearly 100,000 individuals were randomly assigned to Vitamin D versus none or placebo, in order to test the hypothesis that Vitamin D is preventive against cancer and cardiovascular disease. The results found that 150 people need to be treated with Vitamin D for five years for one life to be saved, but among those 149 who were not helped, there were a host of unwanted side effects, including kidney stones, fatigue, pancreatitis, and bone pain. We don’t know about the long-term effects of Vitamin D therapy, and newer evidence now links an excess of Vitamin D to mortality. There remains much work to do.

How You Think, What You Do

When it comes to choosing which treatment option is best for you, you may find yourself largely on your own. You’ll have to gather information and apply the fourfold table. For alternatives that carry similar risks, the decision can be difficult. Part of the reason for this is that people differ greatly in the amount of risk they are willing to take, and the amount of discomfort (both psychological and physical) they’re willing to endure. This side of the patient decision-making process is covered very well in Jerome Groopman and Pamela Hartzband’s book Your Medical Mind.

What are your biases regarding medicine? We all have them. Groopman and Hartzband describe four types of patients: minimalist, maximalist, naturalist, and technologist. A medical minimalist tries to interact with medicine and doctors as little as possible. A maximalist thinks every problem, every ache and pain, has a medical solution. A naturalist believes the body can cure itself, perhaps with the aid of plant-based and spiritual remedies. A technologist believes there are always new drugs or procedures that are better than anything that came before them, and that they will be the most effective route to follow.

These represent extreme types; most of us have some of each of these in us. You might be a minimalist regarding your dental care, but a maximalist for botox and other “youth preservation” procedures. You could be a naturalist when it comes to colds and flus, but a technologist if you need surgery for a ruptured appendix. And these orientations interact. There are certainly maximalist naturalists who have shelves of herbal remedies, and there are minimalist technologists who do as little as possible but, if they need surgery, will request the latest high-tech robot-guided laser surgery with the 1.21 gigawatt flux capacitor guidance system. Understanding your own biases can lead to more efficient decision-making, and a far more productive doctor-patient dialogue. It can be especially helpful to tell your doctor outright which of these styles you lean toward.

But the value of simply understanding the probabilities, how the numbers look on a fourfold table, is always useful and will prove to be so again and again no matter what your personality.

You will hear that if you take some remedy, or follow some new regimens, you will reduce your risk of getting disease X by 50%. That sounds like a no-brainer. But keep those base rates in mind. Consider the forty-year-old woman who was contemplating children, and was told that, given her age (a Bayesian way of framing the problem), a particular birth defect is 5 times more likely. Suppose there was only a 1 in 50,000 chance for a younger woman to have a child with this birth defect, and the chance for the forty-year-old has risen to 1 in 10,000. It is still a very unlikely occurrence. The base rate of the defect is sufficiently low that even a fivefold increase in risk, although impressive in percentage terms, doesn’t have any practical implications. If this reminds you of the statistical shenanigans in Chapter 4 concerning lower divorce rates for people who met online, you’re absolutely right. A 25% reduction in a divorce rate, from 7.7% to 6%, doesn’t have any real-world significance. An increase or reduction in risk like this can pass tests of statistical significance (mainly of concern to researchers) but still not make a meaningful difference.

Alternatively, if you are facing an 80% chance of a catastrophic outcome and you can reduce that by 25%, to a 60% chance, this seems worth doing—the 25% reduction is more meaningful at the top end of the scale. Just about all of us have this personality. We know because of ideas worked out in psychology and behavioral economics, known as prospect theory and expected utility. For most of us nonrational human decision-makers, losses loom larger than gains. In other words, the pain of losing $100 is greater than the pleasure of winning $100. To put it another way, most of us would do more to avoid losing a year of life than we would to gain a year.

One of Kahneman and Tversky’s many great insights was that both gains and losses are nonlinear, meaning that the same amount of gain (or loss) does not cause equal happiness (or sadness)—they’re relative to your current state. If you are broke, gaining one dollar is very important. If you are a millionaire, it is not. There are other nonlinearities: Suppose you’ve just been diagnosed with a particular disease, and your doctor recommends a treatment that will increase your chance of recovery by ten percentage points. The 10% increase feels different, depending on your initial chance of recovery. Consider the following scenarios:

a. Increase your chance of recovery from 0% to 10%.

b. Increase your chance of recovery from 10% to 20%.

c. Increase your chance of recovery from 45% to 55%.

d. Increase your chance of recovery from 90% to 100%.

If you’re like most people, scenarios A and D seem more compelling than B and C. Scenario A changes a certainty of death to a possibility of life. It’s a small possibility, but we are programmed to cling to life and to look at the bright side when faced with alternatives such as this. Scenario D changes a possibility of death to a certainty of life. We jump at the chance of A or D; we want more information about B and C to decide if they’re worth it.

Our intuitive system is not well configured to understand statistics or to make rational decisions in every case—this is the principal point behind Daniel Kahneman’s Thinking, Fast and Slow. As an example, most of us are so sensitive to how a problem is presented—the way it is framed—that simple, even ridiculous manipulations can dramatically influence choices and preferences. For example, consider the following hypothetical data about outcomes of cancer surgery versus radiation. Which would you choose?

1a. Of 100 people having surgery, 90 live through the procedure, and 34 are alive at the end of five years.

1b. Of 100 people having radiation therapy, all live through the treatment, and 22 are alive at the end of five years.

If you chose surgery, you’re like most people—the five-year outcome seems more appealing, even when pitted against the fact that the immediate outcome is better with the radiation.

Now the data are reframed in terms of mortality instead of survival—which would you prefer?

2a. Of 100 people having surgery, 10 die during the procedure, and 66 die by the end of five years.

2b. Of 100 people having radiation therapy, none dies during treatment, and 78 die by the end of five years.

These two formulations of the problem, or frames, are clearly identical mathematically—10 people out of 100 dying is the same as 90 people out of 100 living—but they are not identical psychologically. People are more likely to choose surgery in the first case and radiation in the second. In the first pair of scenarios, our attention is apparently drawn to the difference in five-year outcomes, where 34% are alive from surgery but only 22% from radiation. The framing of the second pair of scenarios apparently draws our attention to the difference in risk of the procedure itself: Radiation reduces the risk of immediate death from 10% to 0%. The framing effect was observed not just in patients but in experienced physicians and statistically sophisticated businesspeople.

Another aspect of framing is that most of us are better with pictures than with raw numbers, one of the motivations for changing the university calculus curriculum to use graphic-based presentations of difficult material. One way that has been tried by doctors to help patients better understand risks is to display visually the various outcomes for a hypothetical group of 100 patients. Here, in this example, are the risks and benefits of treatment with antibiotics for a middle-ear infection (otitis media). The number needed to treat is 20 (out of 100 people who are given antibiotics, 5 people will benefit). In addition, 9 people will not be cured and will need further follow-up. Of the group, 86 are neither helped nor harmed—at least not physically (perhaps financially). This is a lot of antibiotics being taken for such a small benefit. But graphics like these help patients to understand the risk and make better decisions because they can see the proportion of people in each category.

Another aspect of everyone’s decision-making psychology is regret. Amos Tversky taught that risk aversion is driven by regret, a powerful psychological force. We tend to make decisions to avoid the regret that may come from having made the wrong decision, even if the choices were starkly contrasted in terms of expected value. Although treatment X may have only a 10% chance of helping, and a high risk of side effects, you may choose it rather than live with the regret of learning later that you were among the 10% who would benefit from it. The emotional cost of regret can be enormous. As one breast cancer survivor put it, “They told me that they didn’t know whether radiation therapy following the surgery would help or not. But I just kept thinking: What if the breast cancer returns and I didn’t get it? I’d feel like such an idiot.”

The two front tires on my car are five years old and there is still plenty of tread in the center, but I noticed some wear on the edges (this can occur from underinflation or lots of mountain driving). I asked a tire specialist about it and he pointed out that after five years, the rubber in tires becomes brittle and can crack, leading the tread and belts to separate from the rest of the tire. Coupled with the low edge tread, the tires have very little protection against hazards and could blow.

Now, I’ve driven for many years, and many hundreds of thousands of miles, and I’ve had only two or three tires blow out in my life. These were not dangerous situations, but they were inconvenient. You pull over, jack up the car, put on a spare, and if all goes well, you’re only half an hour late to an appointment and you’ve only gotten your clothes a little dirty. On the other hand, if this had happened during a rainstorm, or on a mountain road or highway with no shoulder, it would have been much more unpleasant and possibly unsafe. Neither my mechanic nor the U.S. Department of Transportation can give me an accurate probability that my particular tires will blow before the center tread wears down to the point that they need to be replaced anyway. Even without that information, my hunch—and the hunch of my mechanic—is that the expected value or benefit of replacing the two tires is much lower than the cost of replacing them.

My friend Allan delights in saving money. I mean, he loves saving money, and always tells us how he bought his dishes at the Dollar Store and clothes at the Salvation Army store. It’s not that he can’t afford more—he has plenty of money—it’s just that he feels like he’s a champion in defying the consumer culture of the modern world. Allan would take great pleasure in boasting that he saved $200 by keeping his old tires, and he’s willing to take his chances on an unknown probability of a future inconvenience. My disposition is that I’m more willing to trade money for convenience and safety. Others like the added assurance and are willing to pay for it. This is essentially what insurance is—if fire insurance were such a good deal for home owners, insurance companies would not be the rich multinational corporations they are; make no mistake, it is a good deal for them. But we like the peace of mind insurance offers. I bought the new tires. (Allan has read this passage and wants me to tell you that he thinks I made a decision driven by irrational fears and that I worry too much over nothing.)

Regret plays a huge role in decisions like this. If I ruin a nice picnic or a nice set of clothes or end up in a crash because I didn’t spend that $200, I’m going to feel like an idiot. If Allan can get two more years of wear out of a pair of old tires, he will gleefully wave $200 cash in my face and tell me I was foolish for being such a worrywart.

Of course medical decision-making is also driven by fear of regret. Some of us are willing to trade inconvenience and discomfort now to avoid even a small, 5% chance of something going wrong and the regret of “If only I had done that thing the doctor recommended! What’s wrong with me?—my life was at stake!” Allan, on the other hand, wants to maximize his pleasure in the moment and values the freedom to do what he pleases, unencumbered by health regimens or medical procedures that are not absolutely necessary today.

The best strategy for organizing medical information in cases like these is to arm yourself with the most accurate statistics attainable, as well as understanding your own biases and your stomach for risks and regret. If you find yourself lost and confused, friends and family are often helpful in reminding you of the core values you have lived your life by.

Medicine, Math, and Making Meaningful Choices

The other chapters in this book have been particularly concerned with attention and memory, but the great boon to making decisions about things that matter is mathematics, the so-called queen of the sciences. It might seem like dull, lifeless arithmetic at times, but to get organized in our thinking about life, we are ultimately going to have to let go of our abiding distaste for what sometimes seems like the inhumanity of probability analysis and mathematical calculations.

At that point in life, when facing a difficult choice with the most serious consequences, when we are scared, perplexed, and frustrated, when life is actually on the line, put your faith in the numbers. Try to gather as much information as you can and work through it with experts. If you need surgery, get it done by someone who has done a lot of them. As the CEO of your own health care, you need to understand how to take the information the doctors give you and analyze it in these fourfold tables, applying Bayesian reasoning, because that will take a lot of the guesswork out of medical decision-making, turning it into numbers that we can easily evaluate, since most of us don’t have the refined intuitions of a Dr. Gregory House.

Take some time to make the decision, and consider it from a mathematical perspective. Talk it over with your doctor, and if your doctor isn’t comfortable discussing statistics, find one who is. It’s important to overcome your reluctance to ask questions or to argue with the doctor. Bring a loved one with you to back you up. Be sure the appointment is long enough—ask the doctor, “How long will you have for me?”

When we’re sick or injured, our life seems to become controlled by experts, but it doesn’t have to be that way. We can take charge of our own diseases, learn as much as we can about them and seek advice from more than one doctor. Doctors are people, too, of course, and they come with many different personalities, styles, and strengths. It’s worth finding one whose style matches your own, who understands your needs and can help you meet them. Your relationship with a doctor shouldn’t be one of parent and child, but one of partners who can work together in the business of achieving a common goal.