Chapter 8

Brushing Up on Basic Arithmetic

In This Chapter

Working with whole numbers, including factors, multiples, and prime numbers

Using parts of numbers, including decimals, fractions, and percentages

Mastering ratios

Practicing a few simple math problems

You may feel like you’re back in middle school with the material in this chapter. Although many of these concepts are fairly easy, you do need a firm grasp of them for answering questions on the GRE. The good news: This is stuff you know, and you just need a refresher.

This chapter covers most of the basic arithmetic concepts, including whole numbers, units of measurement, decimals, fractions, percentages, and ratios featured on the GRE. After reading this chapter and practicing the concepts described within, you’ll be armed and ready for any basic math question the GRE throws at you.

Eyeing Integers, Factors, and Multiples

You must be familiar with the following types of numbers for the GRE. Many of the GRE math questions use these terms, and the GRE expects you to know what they are. For example, the question states, “x is an integer” or “x is a factor of 21.”

Integers: Any whole number, positive or negative, is an integer. Zero is neither positive nor negative, but it’s considered an integer. Integers include –3, –2, –1, 0, 1, 2, and 3.

Real numbers: Any number that goes on the number line is considered a real number. These numbers include all negative and positive fractions, decimals, whole numbers, and zero.

Non-real numbers: Any number that can’t exist in real math and, therefore, isn’t on the number line is a non-real number. Mathematics has several types of non-real numbers, but you only need to worry about two for the GRE:

• The square root of a negative number (see Chapter 9)

• Any number divided by zero

Factors: Any integer that you get from dividing another integer is a factor. For example, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. Note that every integer is a factor of itself and 1 is a factor of every number.

Multiples: Any integer you get from multiplying another integer is a multiple. The multiples of 3 begin with 3, 6, 9, 12, and 15, but they go on infinitely. Like factors, every integer is a multiple of itself.

Prime numbers: Any integer that has exactly two factors (1 and itself) is a prime number. I discuss prime numbers in greater detail in the next section.

Factoring in Prime Time: Prime and Composite Numbers

All whole positive numbers are either prime or composite. A prime number is a positive integer (whole number) that has exactly two positive factors: 1 and itself. Examples include 2, 3, 5, 7, and 11.

These little rules about prime numbers can help you better identify them:

Zero isn’t a prime number, because it’s divisible by more than two factors. Anything times zero is zero.

One isn’t a prime number, because it has only one factor: itself.

Two is the only even prime, because it’s the only even number with exactly two factors: 1 and itself.

Meanwhile, composite numbers have more than two factors and can be divided by more than just 1 and themselves. Examples include 4, 6, 8, and 9.

A composite number can be broken down to its prime factors. For example, 36 can be broken down to 2 × 2 × 3 × 3; 84 can be broken down to 2 × 2 × 3 × 7; and 125 can be broken down to 5 × 5 × 5.

Here’s a GRE question example that challenges your grasp of prime numbers:

A Quantity A is greater.

B Quantity B is greater.

C The two quantities are equal.

D The relationship cannot be determined from the information given.

In Quantity A, the prime numbers from 0 to 10 inclusive are 2, 3, 5, and 7. In Quantity B, the prime numbers from 11 to 20 inclusive are 11, 13, 17, and 19. Both quantities have four prime numbers, but counting 0 and 1 as prime would lead you to choose Choice (A), which is incorrect. The correct answer is Choice (C).

Reading between the Lines: Absolute Value

The absolute value, indicated by two vertical parallel lines, is the positive form of a number. Technically, absolute value refers to the distance from zero on the number line. This means that because –7 is 7 units away from zero, the absolute value of –7, written as |–7|, is 7.

Here’s the type of absolute value concept you may encounter on the GRE:

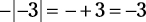
The answer may seem counterintuitive. Isn’t a negative number times a negative number a positive number? Yes, but this problem is actually a negative times a positive. Because the absolute value of –3 is 3, you multiply positive 3 by the negative to get –3.

Here’s a trickier example:

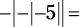
The official way to solve the problem is to work from the inside out. Say to yourself as you go along, “The absolute value of –5 is 5. Then the negative of that is –5. But the absolute value of –5 is 5. And finally, the negative of that is –5.”

Remembering the Order of Things: Putting PEMDAS to Use

When you encounter a problem on the GRE that includes several different operations, such as addition, subtraction, multiplication, division, squaring, and so on, you should do them in a particular order to reach the correct answer. Here is the order:

1. Parentheses: Solve what’s in parentheses first. If you have parentheses inside other sets of parentheses, work from the inside out.

2. Exponents: Squaring, cubing, or using whatever other exponent is next.

3. Multiplication or Division: Work from left to right and solve.

4. Addition or subtraction: Again, solve from left to right.

The best way to remember the order of operations is to use the phrase “Please Excuse My Dear Aunt Sally” (PEMDAS), which stands for parentheses, exponents, multiplication, division, addition, and subtraction. Use PEMDAS for the following problem.

10 (3 – 5)2

Start with what’s inside the parentheses: 3 – 5 = –2. Then move on to the exponents: –2 squared equals 4. Finally, do the multiplication: 4 × 10 = 40.

The GRE tests your ability to approach these questions analytically, which means thinking outside the established methods. PEMDAS is a good rule, but blindly following any rule, including PEMDAS, could turn an easy question into a difficult question. Instead, take a high-level look at any math question before trying to solve it.

Say you have the following problem:

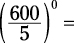
You could begin with dividing 600 by 5 before raising it to the 0 power. But wait a second — anything to the 0 power equals 1. By taking a high-level look at the question before trying to solve it, you save yourself the effort of working the parentheses first.

Measuring Up: Units of Measurement

In conversion questions, the GRE always tells you the relationship between two units of measurement, except for units of time; for example, you won’t be told that 60 seconds = 1 minute.

If you’re asked how many ounces are in 5 pounds, the GRE includes the units of measurement (1 pound = 16 ounces). To solve it, do the following steps:

1. Set the conversion equation up as fractions to avoid mixing up the multiplying and dividing.

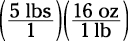
2. Cancel the common terms.

In this example, you cancel the lb units:

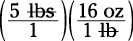
3. Multiply fractions.

When dealing with area and volume, always convert to the smallest unit in the question before calculating. For example, 2 yards by 2 yards might be 4 yards, but if converting to feet, you should convert before calculating. This way you get the correct answer of 36 square feet (from 6 feet by 6 feet) instead of the incorrect answer of 12 square feet (from 4 square yards).

If 12 inches are in a foot, then how many square inches are in a square foot? If you say 12, you’ve fallen for the trap. Why? Because 12 × 12 = 144, which is the actual number of square inches in a square foot.

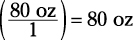
Here’s how you may fall for that trap in an otherwise easy problem:

A Quantity A is greater.

B Quantity B is greater.

C The two quantities are equal.

D The relationship cannot be determined from the information given.

Your first reaction is to think that the quantities are equal because there are 12 inches to a foot and 12 × 3 = 36. However, because a square foot has 144 square inches, and 144 × 3 is definitely greater than 36 (don’t waste any time doing the math), the answer is Choice (A).

Bonus: How many cubic inches are in a cubic foot? Twelve inches per side cubed is 123, which equals 1,728 cubic inches. (For more on 3-D geometric shapes, turn to Chapter 10.)

Discovering the Point with Decimals

Working with decimals isn’t overly difficult. All you have to do is remember a few key points:

Line up the decimal points when adding or subtracting.

Count the decimal places when multiplying.

Move the decimal points of both numbers when dividing.

Though the GRE features an on-screen calculator, you really don’t need it, even with decimal-based math problems. Figuring out how decimals work is easy. The following sections walk you through adding, subtracting, multiplying, and dividing decimals.

Reducing your reliance on the calculator is a sure way to boost your score. Not only can you work problems on scratch paper faster than in the calculator, but you also can make an unnoticed typo on the calculator, which can lead to a wrong answer.

Adding and subtracting decimals

To add or subtract decimals accurately, first line up the decimal points. Then add or subtract as usual, placing the decimal point in the answer right below where it falls in the original numbers.

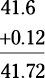
After you line up the decimals, you can add or subtract as usual.

Multiplying decimals

When multiplying decimals, you want to ensure the number of decimal places in the answer is the same as the total number of decimal places in all the numbers you’re multiplying. Multiply the numbers first, and then count the decimal places.

0.06 × 0.03 = 0.0018

You know that 6 × 3 is 18. But the 0.06 and the 0.03 each has two decimal places, for a total of four. Therefore, the final answer also has four decimal places.

Don’t forget to include the zeros at the end when counting the decimal places. After you have your answer, you can drop the end zeros.

0.04 × 0.05 = 0.0020 = 0.002

You know that 4 × 5 is 20, so be sure to include the entire 20 (two and zero) when counting the decimal places. After you have the decimal set correctly, you can drop the right-side zero.

Dividing decimals

Before dividing decimals, turn the decimals into integers by moving the decimal points of both numbers to the right the same number of spaces, until both numbers are whole numbers.

A tricky 0.032 ÷ 0.008 becomes an easy 32 ÷ 8 for a final answer of 4.

Facing Off with Fractions

You probably mastered fractions back in middle school. With some brushing off of the cobwebs, you can master them again. The following sections point out how to add, subtract, multiply, and divide fractions and how to handle mixed numbers.

Adding or subtracting fractions

You can add and subtract fractions only with a common denominator (the same bottom part of the fraction). After the fractions you’re adding or subtracting have been modified to contain the same denominator, you add or subtract the numerator (the top part of the fraction).

To find a common denominator, you can multiply all the denominators. Doing so, however, doesn’t give you the lowest common denominator. Check out this example:

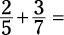
Here, 5 and 7 are different denominators, so you can’t add these two fractions. However, make the denominators the same, and then you can add them.

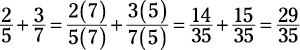
Make sure to multiply the top and bottom of the fraction by the same number to avoid changing the value of the fraction. After the denominators are the same, you can add the fractions. The common denominator will carry over to the answer, but the numerators will add together (or subtract from each other) to give you the final answer.

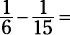
Here’s how to find the lowest common denominator of 15 and 6: You can multiply 15 × 6, but that’s not the lowest common denominator, and that would create a lot of extra work. Instead, count by 15s, because 15 is the larger of the two numbers.

Check each multiple of 15 for divisibility by 6. Does 15 work? No, 6 doesn’t go into 15. How about 30? Yes, both 15 and 6 go into 30. There you have it: The lowest common denominator is 30.

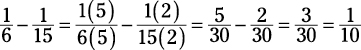
Multiplying fractions

To multiply fractions, you just go straight across, multiplying the numerators with each other and the denominators with each other.

Always check whether you can cancel out common factors between a numerator and a denominator before you begin multiplying in order to avoid dealing with big, awkward numbers and having to reduce fractions at the end. Canceling in advance just makes the numbers smaller and easier to work with.

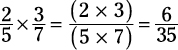
For example, in these fractions, both the 6 and the 9 are divisible by 3. You can cancel those 3s from the numerator and denominator before multiplying the fractions.

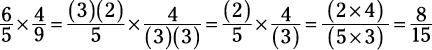
In this next example, the 4 and the 8 reduce (both are divisible by 4), and the 15 and the 5 reduce (both are divisible by 5), simplifying the problem:

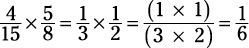
Dividing fractions

To divide two fractions, you invert the second fraction (turning it upside down) and then multiply the two fractions. See this example:

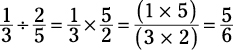
Mixed numbers

A mixed number is a whole number with a fraction tagging along behind it, such as , ,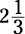

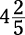or 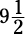. Before you can work with a mixed number (and then add, subtract, multiply, or

divide by it), you first have to get it into fraction form. To do so, multiply the denominator (bottom number) by the whole number and add that to the numerator (top number). Then put the sum over the denominator.

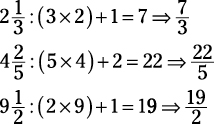
To convert an improper fraction back to a mixed number, count the number of times the denominator goes into the numerator, put that down as the whole number, and then the amount left over goes over the original denominator.

For example, to convert 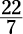into a mixed number, here’s what you do:

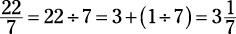
Manipulating Percentages

Percentage-based questions are easy if you know how to work them. The GRE test writers will probably throw a couple percentage-related questions at you to make sure you know how to work them. This section shows you how to convert the percentages into easier forms to work with and how to use formulas to find the answers to the GRE questions.

Converting between percentages and decimals or fractions

When the GRE gives you a percentage-based math question, you don’t have to work it as such. Converting the percentage to a decimal or fraction can make the question much easier to answer. You may need to convert back to a percentage to put the answer in the right form. Just do the following:

To convert a percentage to a decimal: Move the decimal point two places to the left of the percentage and drop the % sign.

35% = 0.35 6% = 0.06 50% = 0.5 3.33% = 0.0333

To convert a decimal to a percentage: Move the decimal point two places to the right and add the % sign.

0.32 = 32% 0.185 = 18.5% 0.05 = 5%

To convert a percentage to a fraction: Place the number over 100, drop the % sign, and reduce if possible.

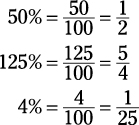
To convert a fraction to a percentage: Set the fraction equal to x over 100 and cross-multiply to find x. The x is your percentage.

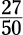becomes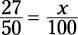

Cross-multiply to solve for x, which equals 54. Therefore, the fraction equals 54%.

Cross-multiplying can be done only with two fractions that equal each other. If you’re missing part of one fraction, place an x where the part is missing, and cross-multiply to find out what x is. Multiply the numerator of the first fraction with the denominator of the second, and set that equal to the product of the denominator of the second fraction with the numerator of the first. It’s simpler in practice than in explanation, as in the following example:

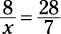
First, multiply the 8 and 7 and set that equal to the 28 times x, giving you

56 = 28x

Then divide both sides by 28 to find the value of x:

2 = x

Finding the percent of change

You may get a question asking you for a percent of change from an original amount. To find this, use this formula:

Percent of change =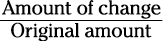

Finding the percent of change requires two simple steps:

1. Find the number (amount) that the item increased or decreased — that is, the amount of change.

For example, if a baseball team won 25 games last year and 30 games this year, the amount of change is 5. If a salesperson earned $10,000 last year and $8,000 this year, the amount of change is 2,000.

2. Place the amount of change over the original amount.

If the team won 25 games last year and 30 games this year, the original amount is 25. If the salesperson earned $10,000 last year and $8,000 this year, the original amount is $10,000.

For the baseball team

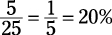
(you divide 1 by 5 to get 0.20 and multiply by 100 to make it a percentage).

For the hapless (meaning unfortunate — think the opposite of happy) salesman,

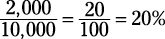
(you again divide 20 by 100 to get 0.20 and multiply by 100 to make it a percentage).

In 2006, Coach Jamieson won 50 prizes at the county fair by tossing a basketball into a bushel basket. In 2007, he won 40 prizes. What was his percent decrease?

A 10

B 20

C 30

D 40

E 50

The number by which Coach Jamieson’s prizes decreased is 10 (from 50 to 40). Place the 10 over the original amount of 50 for a decrease of 20%. The correct answer is Choice (B).

Carissa has three quarters. Her father gives her three more. Carissa’s wealth has increased by what percent?

A 50

B 100

C 200

D 300

E 500

Did you fall for the trap answer, Choice (C)? Carissa’s wealth has doubled, to be sure, but the percent increase is only 100. You can prove that with the percent of change formula. The number increase is 0.75 (she has three more quarters, or 75 cents), and her original whole

was 0.75. So if you follow the formula, you get 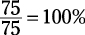. The right answer is Choice (B).

When you double something, you increase it by 100%, because you must subtract the original that you began with. When you triple something, you increase it by 200%, because you must subtract the original you began with. For example, if you had $3 and you now have $9, you’ve tripled your money, but you’ve increased it by only 200%.

Making Ratios More Rational

After you know the tricks, ratios are some of the easiest problems to answer quickly. A ratio is a proportional relationship between two similar numbers or quantities. A ratio is written

as either 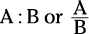. For example,

The ratio of yachts to sailboats = yachts : sailboats

The ratio of umbrellas to people =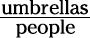

The following sections look at two ways to solve simple ratios and the best way to handle combined ratios.

Considering the total number of items

Because ratios compare the amounts of two different things, the total number of items is a multiple of the sum of the numbers in the ratio. In other words, if the ratio is 3 dogs for every 2 cats, then the total number of dogs can’t be 7 — it has to be 3, 6, or 9, or any multiple of 3. Same with the cats: The number has to be a multiple of 2. You first need to find the sum of the numbers in the ratio: 3 + 2 = 5. So the total number of animals has to be a multiple of 5, with 3 for the dogs and 2 for the cats.

You may encounter a problem like this on the GRE:

At a game, the ratio of your team’s fans to the other team’s fans is 4:5. Which of the following can be the total number of fans at the game?

To solve this ratio problem, you first add the numbers in the ratio: 4 + 5 = 9. The total number of fans must be a multiple of 9 (9, 18, 27, 36, and so on). The total number of fans must be divisible by 9. Can the total, for example, be 54? Yes, because 9 goes evenly into 54. Can it be 64? No, because 9 doesn’t go evenly into 64.

While trying to get Willie to turn down his stereo, his downstairs neighbor pounds on the ceiling and shouts up to his bedroom. If she pounds 7 times for every 5 times she shouts, which of the following can be the total number of poundings and shouts?

A 75

B 57

C 48

D 35

E 30

Add the numbers in the ratio: 7 + 5 = 12. The total must be a multiple of 12 (meaning it must be evenly divisible by 12). Only Choice (C), 48, is evenly divisible by 12. Choices (A), 75, and (B), 57, try to trick you by using the numbers 7 and 5 from the ratio. Choice (D) is a trap with the product of 7 and 5. The correct answer is Choice (C).

Notice how the questions ask which answers can be the possible totals (any multiple of the sums). They’re not asking “which of the following is the total,” in which case you’d need more information to answer the question.

A Quantity A is greater.

B Quantity B is greater.

C The two quantities are equal.

D The relationship cannot be determined from the information given.

You know the total must be a multiple of 11, but it can be an infinite number of terms: 11, 22, 33, 44, 55, and so on. This trap has destroyed many overly confident test-takers through the years. The correct answer is Choice (D).

Finding the amount of a specific term

When you’re given a ratio and a total and are asked to find the amount of a specific term, one way to solve the ratio is to do the following:

1. Add the numbers in the ratio.

The total number of items is a multiple of this sum.

2. Divide the total number of items by that sum.

3. Multiply that quotient by each term in the ratio.

4. Add the answers to double-check that they add up to the total.

Be sure to do this step to check your work.

It takes longer to explain these steps than it does to work them. With a little practice, the technique becomes second nature. Consider this example:

Congratulating the members of his team, which had just won 21 to 0, the ecstatic coach ­gestured to each member of the squad, calling everyone either a champ or a winner. If there were 3 champs for every 4 winners, and every member of the 28-man squad was either a champ or a winner, how many champs were there?

There are 3 champs for every 4 winners, so add the numbers in the ratio: 3 + 4 = 7. Then

divide that sum into the total number of players: 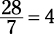. Now multiply that number by each

term in the ratio: 3 × 4 = 12 champs; 4 × 4 = 16 winners. The question asks for the number of champs, so the correct answer is 12. Finally, add the answers to double-check that they sum up to 28: 12 + 16 = 28.

If the GRE math problem features an existing ratio, and you have to change the number of items while maintaining the ratio, you can easily calculate the number of items you need by setting up a proportion, which is two ratios (fractions) set equal to each other. Make the existing ratio (as a fraction) equal to the new items (also as a fraction), and cross-multiply to find the missing value.

Your college has to maintain its current ratio of 3 graduate assistants for every 40 students. If 240 new students are expected this fall, how many new graduate assistants should the school hire to maintain the ratio?

1. Set up the existing ratio as a fraction.

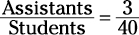
2. Set up the new additions as a fraction, with x as the unknown value.

3. Set the fractions equal to each other.

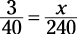
4. Solve for x.

Cross-multiply, multiplying the numerator of each fraction by the denominator of the other:

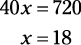
Thus, 18 new graduate assistants are needed to maintain the ratio.

Combining two or more ratios

Sometimes the GRE provides you with two different ratios. However, one item is common in each of the ratios. For example, a jazz shop has 6 saxophones for every 5 drum kits and 2 drum kits for every 3 trombones. You can use the common item (drum kits) to combine the ratios for a single ratio of instruments at the jazz shop.

Combining ratios is a little like adding fractions. When adding fractions, you find the lowest common denominator. Ratios don’t have numerators or denominators, but they do have something in common — in this case, drum kits. In order to combine ratios, follow these simple steps.

Sam’s jazz shop has 6 saxophones for every 5 drum kits and 2 drum kits for every 3 trombones. What’s the ratio of saxophones to trombones?

1. Set up the ratios as A : B.

Place the item that the ratios have in common (drum kits) into a column.

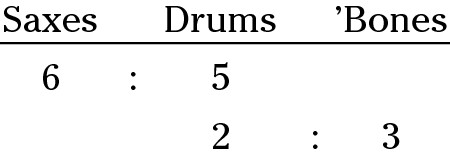
2. Find a common multiple for the item that these ratios have in common.

In this instance, both ratios include drum kits. The least common multiple of 5 and 2 (the numbers of drum kits) is 10.

3. Multiply each term in the ratios so that the quantity of the item in common equals the common multiple (from Step 2).

Now, if you were adding these as fractions, you’d write the drums as the denominators, and your work would start out like this:

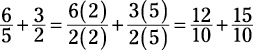
Of course, you aren’t adding fractions, but you treat the ratios the same way: Multiply both terms of each ratio by the same number, as though you’re getting a common denominator. Here, you want the number of drum kits to equal 10. Multiply both terms in the first ratio by 2, and multiply both terms in the second ratio by 5:

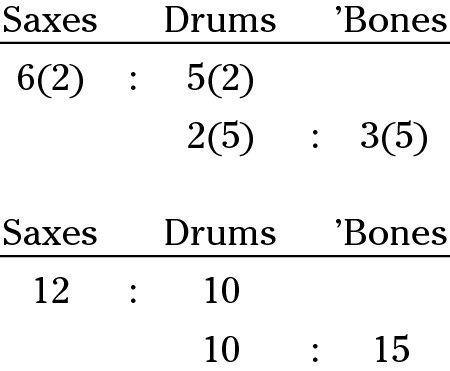
4. Write out a combined ratio.

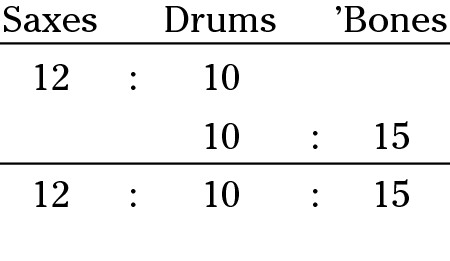
The combined ratio of saxophones to drum kits to trombones is 12:10:15. To answer the question, give only the ratio of saxophones to trombones, which is 12:15, or 4:5.

Working the Numbers: Arithmetic Practice Problems

Now it’s your turn. Each of these practice questions is based on at least one concept discussed earlier in this chapter. If you get stuck, don’t hesitate to flip back a few pages to review some step-by-steps. The concepts in this chapter are central to the GRE Math section, so being able to solve and understand these practice problems is important.

1. After a rough hockey game, Bernie checks his uniform and finds 3 smudges for every 5 tears. Which of the following can be the total number of smudges and tears on Bernie’s uniform?

A 53

B 45

C 35

D 33

E 32

Add the numbers in the ratio: 3 + 5 = 8. The total must be a multiple of 8 (or, looking at it another way, the total must be evenly divisible by 8). Only Choice (E) is a multiple of 8 (8 × 4 = 32). The correct answer is Choice (E).

2. Banker’s Credit Union has 7 call-center reps on hand for every 200 customers. With an aggressive marketing campaign, the bank just signed up an additional 1,400 customers. How many new reps should the bank hire in order to maintain this ratio?

A 14

B 20

C 35

D 49

E 50

Set up the equation:

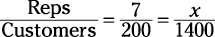
Cross-multiply, and you find that x = 49. The correct answer is Choice (D).

3. A sports shop has 3 jerseys for every 2 helmets and 6 kneepads for every 5 jerseys. What’s the ratio of helmets to kneepads?

A 1:3

B 4:9

C 5:9

D 2:3

E 7:9

Set up the ratios:

Find a common multiple of jerseys. A common multiple of 3 and 5 is 15, so multiply each term of the first ratio by 5 and each term of the second by 3:

Write them out as a combined ratio:

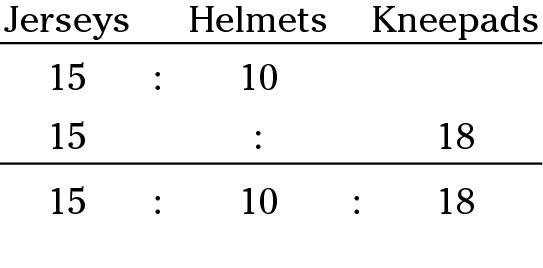
The ratio of helmets to kneepads is 10:18, or 5:9, so the correct answer is Choice (C).