Chapter 10
Shaping Up Your Geometry Skills
In This Chapter
 Getting straight with lines and angles
Getting straight with lines and angles
 Working with polygons
Working with polygons
 Tackling a host of triangle and quadrilateral questions
Tackling a host of triangle and quadrilateral questions
 Conquering common circle questions
Conquering common circle questions
 Calculating the volume and surface area of solids
Calculating the volume and surface area of solids
Geometry is all about the mathematics locked in lines, angles, triangles, rectangles, squares, circles, cubes, tubes, and more. This chapter introduces you to the many shapes you’re likely to encounter on the GRE and the corresponding equations required for answering geometry questions. You also get some hands-on practice answering a few sample questions at the end.
Exploring Lines and Angles
The fundamental components of many geometric shapes are lines and angles, so before tackling shapes, wrap your brain around lines and angles.
Lines
You’ve probably heard the term straight line, but in geometry, that phrase is a little redundant. All lines are straight. If a line curves, it’s not a line — it’s a curve. Also, unless a line is specifically referred to as a line segment, assume it goes on forever. If the line has one endpoint (point where the line starts) and the other end has an arrow indicating it goes on forever, it’s a ray.
Parallel lines never cross and are represented by the symbol ||. Perpendicular lines cross at right angles and are represented by the symbol ⊥. A perpendicular bisector is a line that passes through the midpoint of a line segment and is perpendicular to it.
Angles
Angles are a big part of GRE geometry problems. An angle basically is the space between two rays that share an endpoint. Fortunately, understanding angles is easy after you memorize the different angle types and a few key concepts, as explained in this section.
Finding an angle is usually a matter of simple addition or subtraction. In addition to the rules in the following sections, these three rules apply to the angles on the GRE:
 You aren’t going to see negative angles.
You aren’t going to see negative angles.
 You aren’t going to see zero angles.
You aren’t going to see zero angles.
 You most likely aren’t going to see any fractional angles. (For example, an angle won’t
You most likely aren’t going to see any fractional angles. (For example, an angle won’t
measure 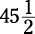 degrees or
degrees or 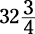 degrees.) On the GRE, angles are whole numbers. If you’re
degrees.) On the GRE, angles are whole numbers. If you’re
plugging in a number for an angle, plug in a whole number, such as 30, 45, or 90.
Right angle
Right angles are 90 degrees and are represented by perpendicular lines with a small box where the two lines meet.
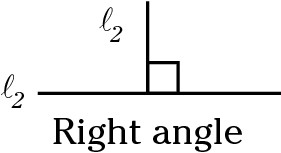
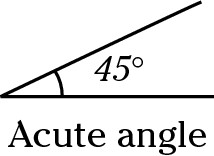
Acute angle
An acute angle is any angle greater than 0 degrees but less than 90 degrees.
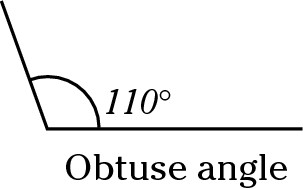
Obtuse angle
An obtuse angle is any angle greater than 90 degrees but less than 180 degrees.
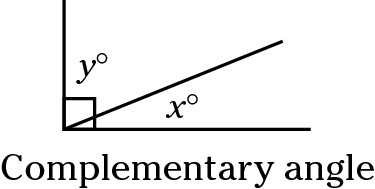
Complementary angles
Complementary angles together form a right angle: 90 degrees.
Supplementary angles
Supplementary angles together form a straight line: 180 degrees.
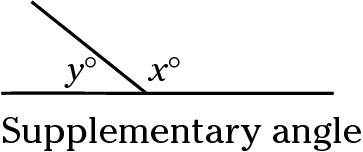
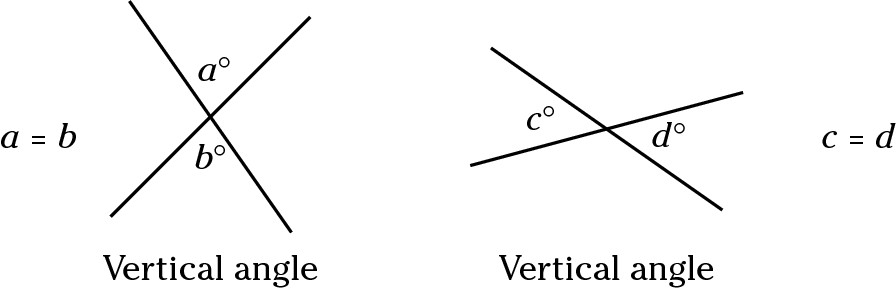
Vertical angles
Vertical angles are the angles opposite one another where two lines cross. Vertical angles have equal measures.
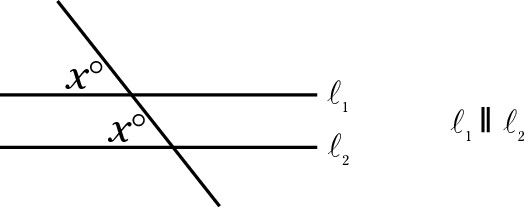
Transversal angles
A transversal is a line that cuts through two parallel lines. Transversal angles are the angles directly across from each other on the parallel lines and have the same measures.
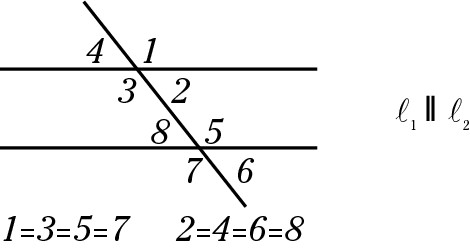
Note that all the odd-numbered angles are equal, as are all the even-numbered angles. Also, never assume the lines are parallel unless the question states that they are or the image indicates parallel lines as in the preceding figure; here,  indicates that the two lines are parallel.
indicates that the two lines are parallel.
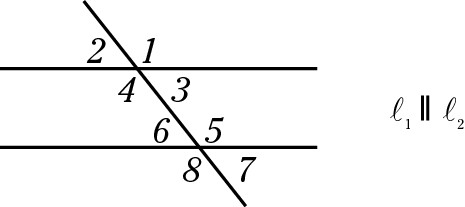
If you zig when you should’ve zagged, the fact that all even-numbered angles are equal to one another and all odd-numbered angles are equal to one another no longer holds true.
Recognizing the Many Sides of Polygons
A polygon is any closed shape consisting of line segments, which qualifies everything from a triangle (three sides) to a dodecagon (a dozen sides) and beyond as a polygon. The polygons you’re most likely going to encounter on the GRE are triangles and quadrilaterals (four sides). Table 10-1 lists the names of a few others you may bump into.
Table 10-1 Polygons
|
Number of Sides |
Name |
|
5 |
Pentagon |
|
6 |
Hexagon (think of x in six and x in hex) |
|
7 |
Heptagon |
|
8 |
Octagon |
|
9 |
Nonagon |
|
10 |
Decagon |
The GRE usually doesn’t ask for the areas of any polygons with more than four sides. It may, however, ask you to find the perimeter, which is just the sum of the lengths of all the sides. The following explains what you do need to know about polygons for the GRE.
Determining total interior angle measure
Because you may be asked to find the total interior angle measure of a particular polygon, keep this formula in mind (where n stands for the number of sides):
(n – 2)180
For example, the interior angles of the following polygons are
 Triangle: (3 – 2)180 = 1 × 180 = 180°
Triangle: (3 – 2)180 = 1 × 180 = 180°
 Quadrilateral: (4 – 2)180 = 2 × 180 = 360°
Quadrilateral: (4 – 2)180 = 2 × 180 = 360°
 Pentagon: (5 – 2)180 = 3 × 180 = 540°
Pentagon: (5 – 2)180 = 3 × 180 = 540°
 Hexagon: (6 – 2)180 = 4 × 180 = 720°
Hexagon: (6 – 2)180 = 4 × 180 = 720°
 Heptagon: (7 – 2)180 = 5 × 180 = 900°
Heptagon: (7 – 2)180 = 5 × 180 = 900°
 Octagon: (8 – 2)180 = 6 × 180 = 1,080°
Octagon: (8 – 2)180 = 6 × 180 = 1,080°
 Nonagon: (9 – 2)180 = 7 × 180 = 1,260°
Nonagon: (9 – 2)180 = 7 × 180 = 1,260°
 Decagon: (10 – 2)180 = 8 × 180 = 1,440°
Decagon: (10 – 2)180 = 8 × 180 = 1,440°
Try another one: 3 × 180. Double the first number: 3 × 2 = 6. Halve the second number:
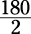 = 90. Then multiply: 6 × 90 = 540.
= 90. Then multiply: 6 × 90 = 540.
Finding one interior angle
If you’re asked to find the average measure of one angle in a polygon, use the following formula:
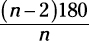
Here, n stands for the number of sides (which is the same as the number of angles). So to find an interior angle of a pentagon:
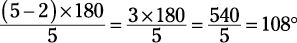
Because all angles are equal in a regular polygon, the same formula applies to one angle in a regular polygon.
Understanding Triangles from Top to Bottom
Although comprised of a mere three sides, the triangle is a key figure in geometry, especially on the GRE. Understand how triangles work, and you’re well on your way to mastering other polygons. The following sections introduce you to the different types of triangles and explain how to do the math related to triangles.
Recognizing triangle types
Triangles come in three basic types: equilateral, isosceles, and right, as described in the following sections.
Equilateral triangle
An equilateral triangle has three equal sides and three equal angles. This can also be called an equiangular triangle.
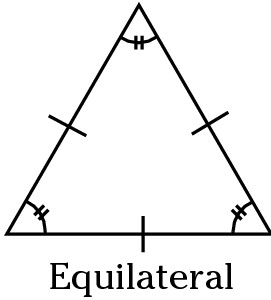
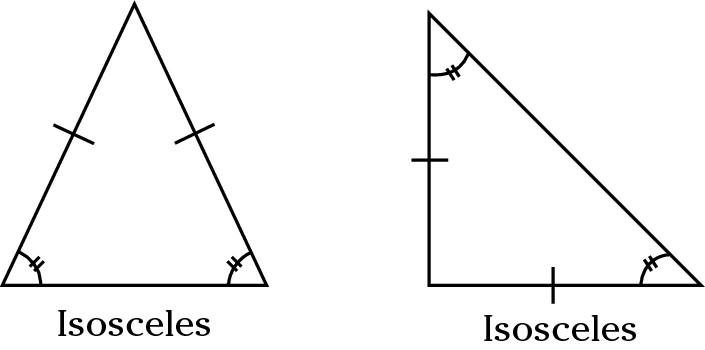
Isosceles triangle
An isosceles triangle has two equal sides and two equal angles. The angles opposite the equal sides are the two equal angles.
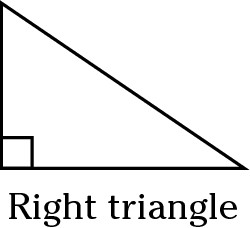
Right triangle
A right triangle has one 90-degree angle.
Noting key characteristics
Triangles have some notable characteristics that you may need to know to field some of the geometry questions on the test. The following points bring you up to speed:
 The largest angle is opposite the longest side. And, as you may surmise, the smallest angle is opposite the shortest side.
The largest angle is opposite the longest side. And, as you may surmise, the smallest angle is opposite the shortest side.
 The sum of any two sides must be greater than the length of the remaining side. This fact is often written as a + b > c where a, b, and c are the sides of the triangle.
The sum of any two sides must be greater than the length of the remaining side. This fact is often written as a + b > c where a, b, and c are the sides of the triangle.
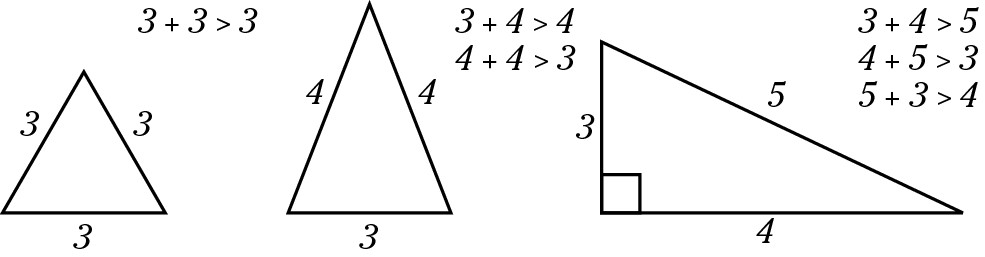
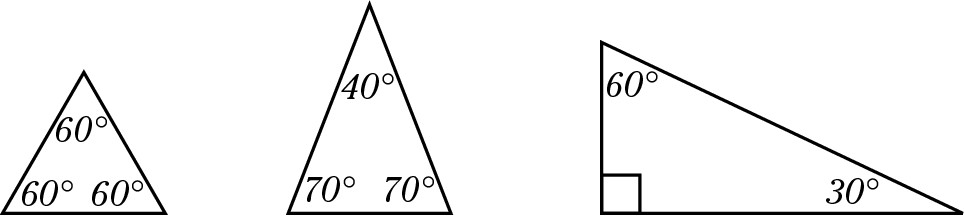
 The sum of the interior angles is always 180 degrees. Just because one triangle is bigger than another doesn’t make the sum of its interior angles any larger. Every triangle’s angles total 180 degrees.
The sum of the interior angles is always 180 degrees. Just because one triangle is bigger than another doesn’t make the sum of its interior angles any larger. Every triangle’s angles total 180 degrees.
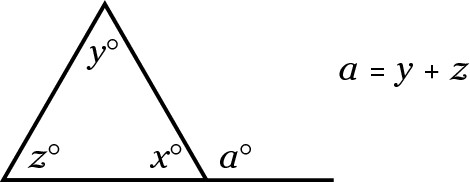
 Any exterior angle is equal to the sum of the two remote interior angles. When you think about this rule logically, it makes sense. The sum of supplementary angles is 180, and x (inside the triangle) and a (outside) are supplementary, so x + a = 180. The sum of the angles in a triangle is 180, and x, y, and z are inside the triangle, so x + y + z = 180. Substitution then gives you x + a = x + y + z. Then you subtract the x from both sides to get a = y + z.
Any exterior angle is equal to the sum of the two remote interior angles. When you think about this rule logically, it makes sense. The sum of supplementary angles is 180, and x (inside the triangle) and a (outside) are supplementary, so x + a = 180. The sum of the angles in a triangle is 180, and x, y, and z are inside the triangle, so x + y + z = 180. Substitution then gives you x + a = x + y + z. Then you subtract the x from both sides to get a = y + z.
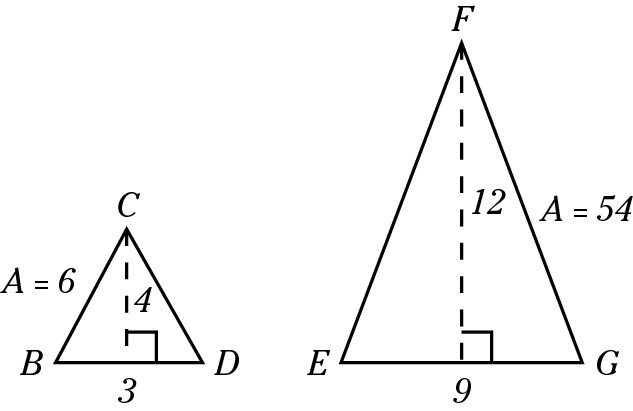
Working with similar triangles
Similar triangles have congruent (identical) angles and proportional sides. For example, if the heights of two similar triangles are in a ratio of 2:3, then the bases of those triangles are in a ratio of 2:3 as well.
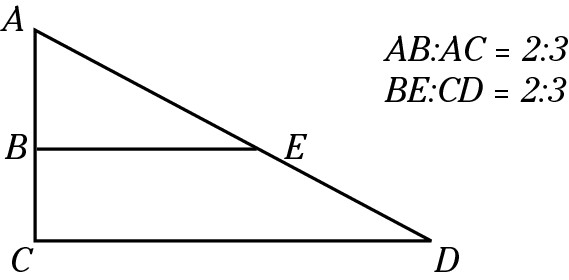
The ratio of the areas of similar triangles is equal to the square of the ratio of their sides.
For example, if each side of triangle BCD is 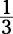 the length of each side of similar triangle EFG,
the length of each side of similar triangle EFG,
then the area of triangle BCD is 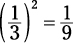 the area of triangle EFG.
the area of triangle EFG.
 Two similar triangles have bases 5 and 25. Which of the following expresses the ratio of the areas of the two triangles?
Two similar triangles have bases 5 and 25. Which of the following expresses the ratio of the areas of the two triangles?
A 1:5
B 1:15
C 1:25
D 2:15
E It cannot be determined from the information given.
The ratio of the sides is 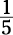 . The ratio of the areas is the square of the ratio of the sides:
. The ratio of the areas is the square of the ratio of the sides:
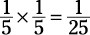 . Note that Choice (E) is a trap for the unwary. You can’t figure out the exact
. Note that Choice (E) is a trap for the unwary. You can’t figure out the exact
area of either figure because you don’t know the height. (The area of a triangle is 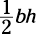 or
or
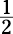 base × height.) However, you aren’t asked for an area, only for the ratio of the areas, which
base × height.) However, you aren’t asked for an area, only for the ratio of the areas, which
you can deduce from information in the question. Correct answer: Choice (C).
Bonus: What do you suppose is the ratio of the volumes of two similar figures? Because volume is found in cubic units, the ratio of the volumes of two similar figures is the cube of the ratio of their sides. If Figure A has a base of 5 and similar Figure B has a base of 10, then
the ratio of their volumes is 1:8 ([1:2]3), which is 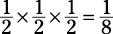 .
.
Calculating a triangle’s perimeter and area
You’re likely to encounter at least one question on the test that asks for the perimeter or area of a triangle. The following sections can help you clear that hurdle.
Calculating perimeter
Perimeter is the distance around a triangle, so add up the lengths of the sides.
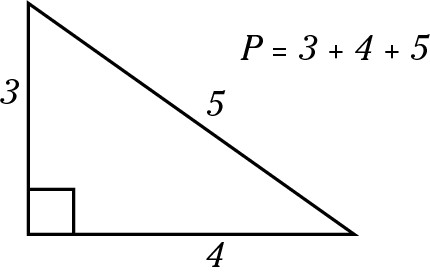
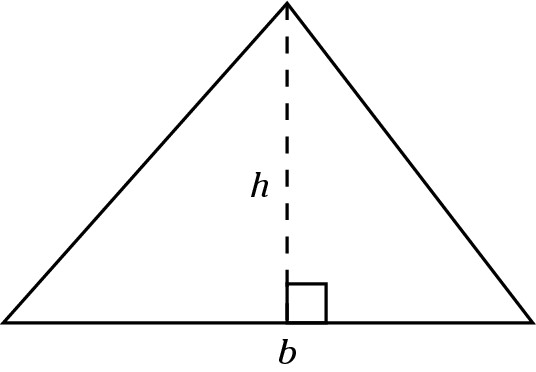
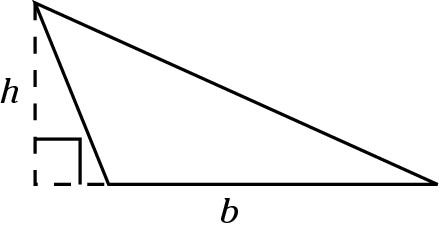
Calculating area
The area of a triangle is 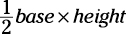 .
.
The height is always a line perpendicular to the base. The height may be a side of the triangle, as in a right triangle.
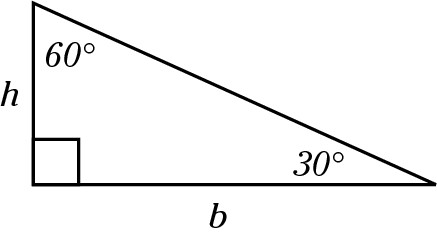
Then again, the height may be inside the triangle. A dashed line and a small 90-degree box often represent the height.
Understanding the Pythagorean theorem
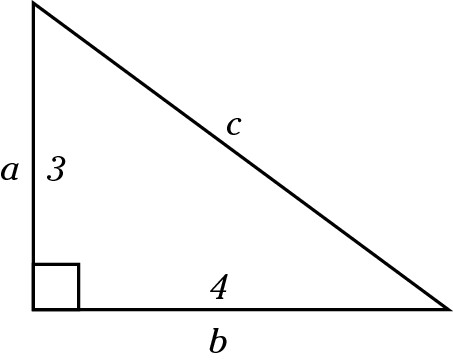
The Pythagorean theorem (PT) states that the sum of the squares of the two sides of any right triangle is equal to the square of the hypotenuse. In any right triangle (and it has to be a right triangle), you can find the lengths of the sides with this formula:
a2 + b2 = c2
Here, a and b are the sides of the triangle, and c is the hypotenuse. The hypotenuse is always opposite the 90-degree angle and is always the longest side of the triangle.
With PT, if you know the lengths of any two sides of a right triangle, you can find the length of the third side by plugging in the numbers and doing the math. For example, say you’re asked for the length of the hypotenuse in this triangle:
Here’s what you do:
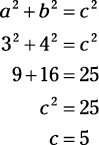
Here’s an example in which you know the length of the hypotenuse and one of its sides:

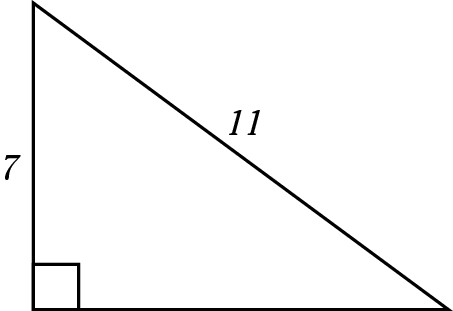
To find the unknown length of the third side, here’s what you do:
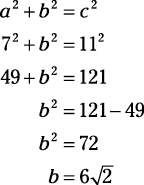
Identifying common Pythagorean ratios in right triangles
Doing the whole PT formula every time you want to find the third side length of a right triangle isn’t always necessary. The following sections clue you in to four very common PT ratios that make your job a whole lot easier.
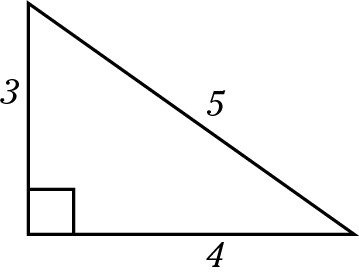
3:4:5
If one side of a right triangle is 3 and the other is 4, then the hypotenuse must be 5. Likewise, if the hypotenuse is 5 and the length of one side is 4, the other side must be 3.
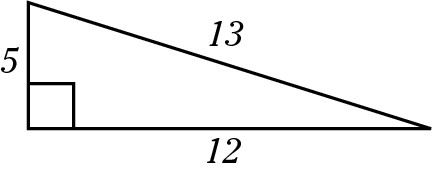
5:12:13
If one side of a right triangle is 5 and another side is 12, then the hypotenuse must be 13. Likewise, if you know the hypotenuse is 13 and one of the sides is 5, then the other side must be 12.
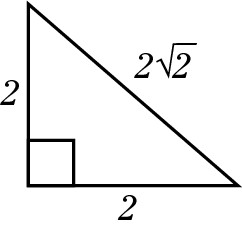
s:s:s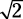
This ratio is exclusively for isosceles right triangles (which of course contain 45-45-90 degree angles), and s stands for side. If one side is 2 and a second side is also 2, then the hypotenuse is 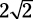 .
.
You can modify the formula to solve problems in which you’re given the length of the hypotenuse of an isosceles right triangle and need to find the length of the other two sides:
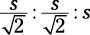
 The diagonal of a square is 5. What is the area of the square?
The diagonal of a square is 5. What is the area of the square?
To determine the area, first you need to know the length of a side, so plug in the numbers:
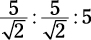
The hypotenuse is 5, and the length of any side of the square is 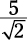 . The area of the square
. The area of the square
is simply 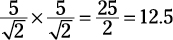 .
.
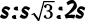
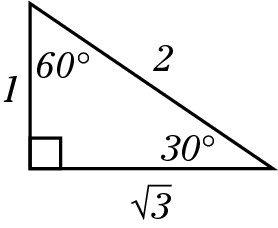
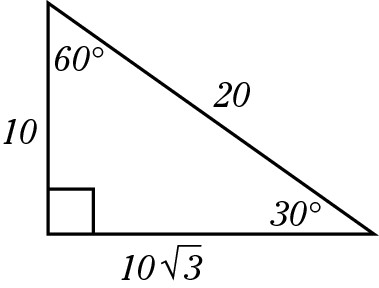
This is a special ratio for the sides of a 30:60:90 triangle, which has angles measuring 30, 60, and 90 degrees. S is the length of the short side (opposite the 30 degree angle), 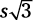 is the longer side, and 2s is the hypotenuse.
is the longer side, and 2s is the hypotenuse.
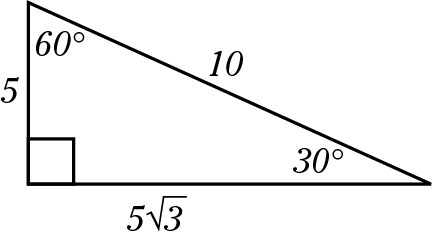
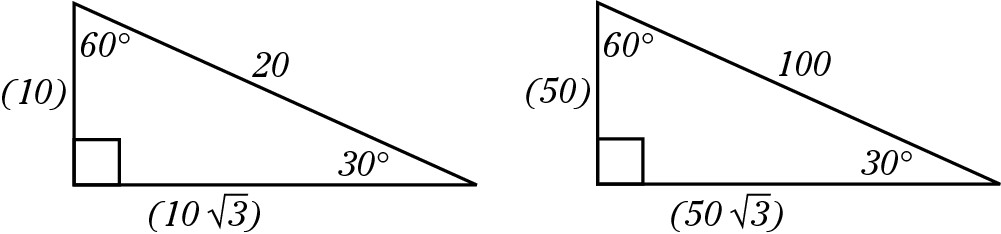
This type of triangle is a favorite of the test-makers. The important fact to keep in mind here is that the hypotenuse is twice the length of the short side (which must be opposite the 30 degree angle). If you encounter a word problem that says, “Given a 30:60:90 triangle of hypotenuse 20, find the area,” or “Given a 30:60:90 triangle of hypotenuse 100, find the perimeter,” you can do so because you can quickly find the lengths of the other sides.
Knowing Quadrilaterals Inside and Out
After you master triangles, quadrilaterals are easy. Any four-sided figure is called a quadrilateral. The interior angles of any quadrilateral total 360 degrees, and you can cut any quadrilateral into two triangles, each of which has total interior angles of 180 degrees. The following sections present everything you need to know about quadrilaterals, including the names of the many types of quadrilaterals.
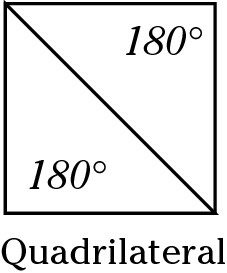
Recognizing a quadrilateral when you see one
Although all quadrilaterals have four sides, the sides can be arranged in numerous configurations to form squares, rectangles, and other types of quadrilaterals, as described in the following sections.
Square
The most famous quadrilateral is the square — a quadrilateral with four equal sides and
four right angles. The area of a square is side2 (base × height), or 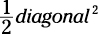 .
.
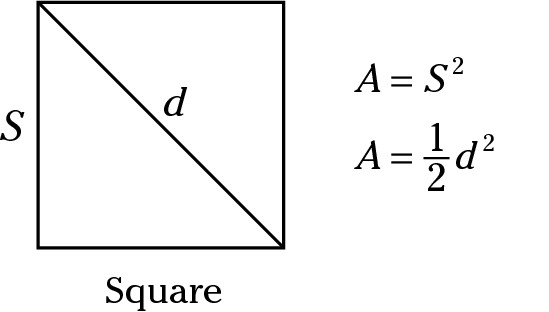
Rhombus
A rhombus is a quadrilateral with four equal sides and four angles that aren’t necessarily right angles. A rhombus often looks like a drunken square — tipsy and wobbly. The area of
a rhombus is 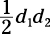 or
or 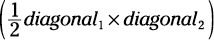 .
.
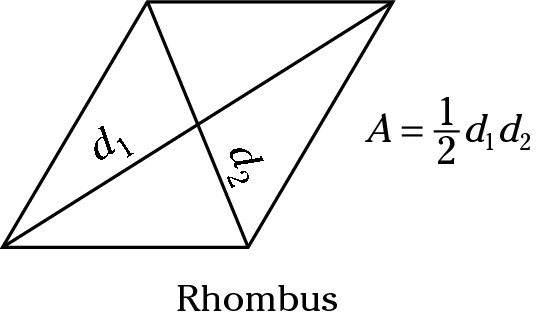
Rectangle
A rectangle is a quadrilateral with two opposite and equal pairs of sides and four right angles. The top and bottom sides are equal, and the right and left sides are equal. (Rectangle means right angle.) The area of a rectangle is length × width (which is the same as base × height).
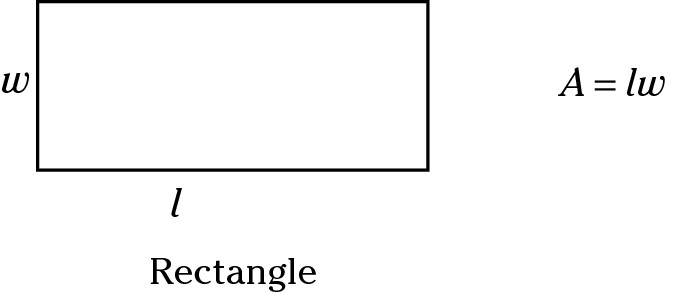
Parallelogram
A parallelogram is a quadrilateral with two opposite and equal pairs of sides. The top and bottom sides are equal, and the right and left sides are equal. Opposite angles are equal but not necessarily right (or 90 degrees). The area of a parallelogram is base × height. Remember that the height is the distance between the two bases, which are the parallel sides, and is always represented by a perpendicular line from the tallest point of the figure down to the base. Diagonals of a parallelogram bisect each other.
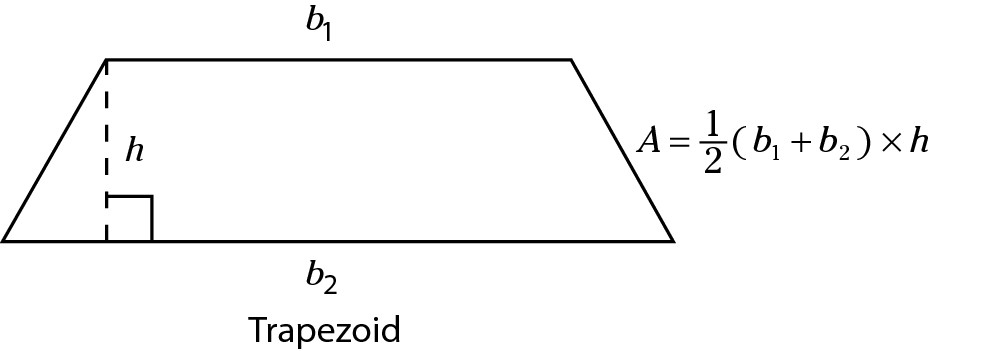
Trapezoid
A trapezoid is a quadrilateral with two parallel sides and two nonparallel sides. The area of a
trapezoid is 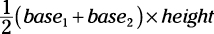 . It makes no difference which base you label base 1 and
. It makes no difference which base you label base 1 and
which you label base 2, because you’re adding them together anyway. Just be sure to add
them before you multiply by 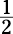 .
.
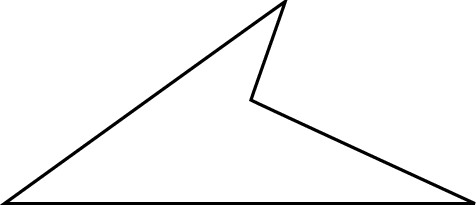
Irregular quadrilaterals
Some quadrilaterals don’t have nice, neat shapes or special names.
Working with Circles
Determining a circle’s circumference (distance around the circle) or area given only its radius (the distance from the center of the circle to its edge) is easy if you know the formulas and characteristics of the circle. The following sections cover the characteristics and the formulas you need to solve problems related to circles.
Recognizing a circle’s characteristics
Circles have several unique characteristics. You need to know what these characteristics are to decipher the terminology used on the test.
 Center: The center is right in the middle of the circle. If a question references the circle by a capital letter, that’s both the circle’s center and its name.
Center: The center is right in the middle of the circle. If a question references the circle by a capital letter, that’s both the circle’s center and its name.
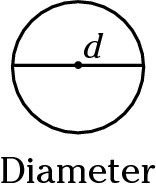
 Diameter: Diameter is the length of a line between two points on opposite sides of the circle that passes through the center of the circle. The diameter is equal to two times the radius.
Diameter: Diameter is the length of a line between two points on opposite sides of the circle that passes through the center of the circle. The diameter is equal to two times the radius.
 Circumference: Circumference is the distance around a circle, its perimeter.
Circumference: Circumference is the distance around a circle, its perimeter.
 π: Pronounced pi, π is the ratio of the circumference of a circle to the diameter of a circle. It equals approximately 3.14, but more often than not, circle-based questions have answer choices in terms of π, such as 2π rather than 6.28.
π: Pronounced pi, π is the ratio of the circumference of a circle to the diameter of a circle. It equals approximately 3.14, but more often than not, circle-based questions have answer choices in terms of π, such as 2π rather than 6.28.
 Radius: Radius is the distance from the center of the circle to the edge of the circle. The radius of a circle is half the diameter.
Radius: Radius is the distance from the center of the circle to the edge of the circle. The radius of a circle is half the diameter.
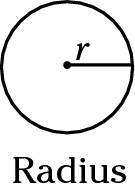
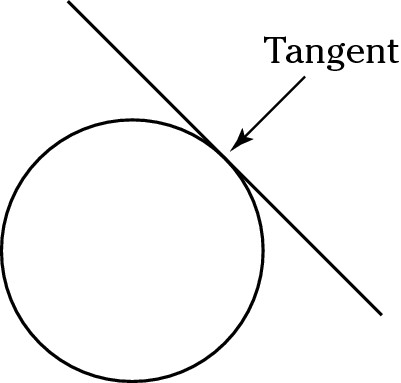
 Tangent: A tangent is a line outside a circle that touches the circle’s perimeter at one point. A line drawn from the center of the circle to the point where the tangent touches the perimeter of the circle forms a right angle to the tangent.
Tangent: A tangent is a line outside a circle that touches the circle’s perimeter at one point. A line drawn from the center of the circle to the point where the tangent touches the perimeter of the circle forms a right angle to the tangent.
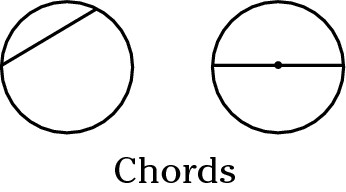
 Chord: A chord is a line that connects any two points on the perimeter of a circle. The longest chord in a circle is the diameter.
Chord: A chord is a line that connects any two points on the perimeter of a circle. The longest chord in a circle is the diameter.
Choose from these answer choices for the two example questions that follow:
A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.


Many people choose Choice (D) for this question. Typically in QCs (Quantitative Comparisons) like this, the correct answer to a geometry question with no figure is Choice (D) because the answer depends on how you draw the picture. However, a circle is frequently an exception. A circle is a circle is a circle; it rarely depends on how you draw it. The key here is to know that the longest chord is a fancy way of saying the diameter. Because the diameter is twice the radius, a circle of diameter (or longest chord) 12 has a radius of 6. Two circles with radii of 6 have the same area. (Don’t waste even a nanosecond figuring out what that area actually is. It’s irrelevant to comparing the quantities.) Correct answer: Choice (C).


If you chose Choice (C), you fell for the trap. Remember that a chord is a straight line that connects any two points on a circle. The longest chord is the diameter, but Quantity B doesn’t specify longest chord. If it were the longest chord, the two quantities would be equal, but if it’s not the longest chord, then the diameter of the circle is greater than 20, making the radius greater than 10, which would make the value of Quantity B greater. In other words, the question doesn’t provide enough information to make a determination. Correct answer: Choice (D).
Mastering essential formulas
Solving circle problems is all about knowing formulas and how to use them. The following sections reveal the formulas and provide guidance on solving problems, complete with sample questions.
Circumference: C = 2πr
Circumference is a fancy word for perimeter — the distance around a circle. The formula is C = 2πr (C is circumference, r is radius, and d is diameter). Because diameter is twice the radius, you may also use the equation C = dπ.
For example, the circumference of a circle with a radius of 3 is
2 × π × 3 = 6π
 A child’s wagon has a wheel of radius 6 inches. If the wagon wheel travels 100 revolutions, approximately how many feet has the wagon rolled?
A child’s wagon has a wheel of radius 6 inches. If the wagon wheel travels 100 revolutions, approximately how many feet has the wagon rolled?
A 325
B 314
C 255
D 201
E It cannot be determined from the information given.
The question gives the radius in inches, but the answer choices are all in feet, so the first order of business is to convert inches into feet: 6 ÷ 12 = 0.5 feet. One revolution is equal to one circumference, so first find the circumference of the circle in feet:
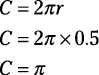
Then multiply by the number of revolutions:
π × 100 = 100π ft
Because π is approximately 3.14, multiply:
3.14 × 100 = 314 ft
Choice (E) is definitely not the answer. If you have a radius, you can solve for nearly anything having to do with circles. Correct answer: Choice (B).
Area: A = πr2
The area of a circle is πr2, so if a circle has a radius of 4, you can find the area by doing the following:
π × 42 = 16π
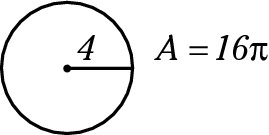
Angles inside a circle
By drawing two lines inside a circle from the center to two points on the circumference or a single point on the circumference to two points on the circumference, you form two types of angles inside the circle:
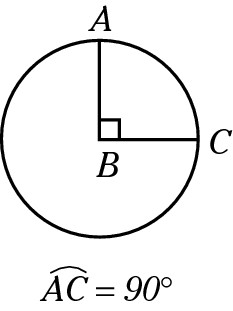
 A central angle has its vertex at the center of a circle and its endpoints on the circumference. The degree measure of a central angle is the same as the degree measure of its intercepted arc (the part of the circle’s perimeter that falls between the two points where the central angle’s lines touch the circle’s perimeter).
A central angle has its vertex at the center of a circle and its endpoints on the circumference. The degree measure of a central angle is the same as the degree measure of its intercepted arc (the part of the circle’s perimeter that falls between the two points where the central angle’s lines touch the circle’s perimeter).
 An inscribed angle has both its vertex and endpoints on the circumference. The degree measure of an inscribed angle is half the degree measure of its intercepted arc, as shown in the following figure. The intercepted arc is 80 degrees, and the inscribed angle is 80 ÷ 2 = 40 degrees.
An inscribed angle has both its vertex and endpoints on the circumference. The degree measure of an inscribed angle is half the degree measure of its intercepted arc, as shown in the following figure. The intercepted arc is 80 degrees, and the inscribed angle is 80 ÷ 2 = 40 degrees.
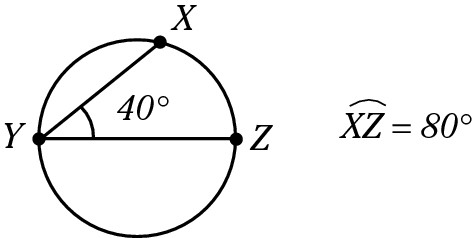
You may see a figure that looks like a dream catcher, with lines running every which way. Take the time to identify the endpoints of the angles and the vertex. You may be surprised at how easy the question suddenly becomes.
 In this figure, find the sum of the degree measures of angles a + b + c + d + e.
In this figure, find the sum of the degree measures of angles a + b + c + d + e.
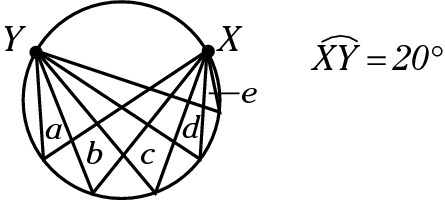
Note: Figure not drawn to scale.
A 65
B 60
C 55
D 50
E 45
Each angle is an inscribed angle. That means the angle has half the degree measure of the central angle, or half the degree measure of its intercepted arc. If you look carefully at the endpoints of these angles, they’re all the same: XY. Arc XY has a measure of 20 degrees. Therefore, each angle is 10 degrees, for a total of 50. Correct answer: Choice (D).
Arcs
An arc is a portion of the circumference of a circle. The degree measure of an arc is the same as its central angle and twice its inscribed angle.
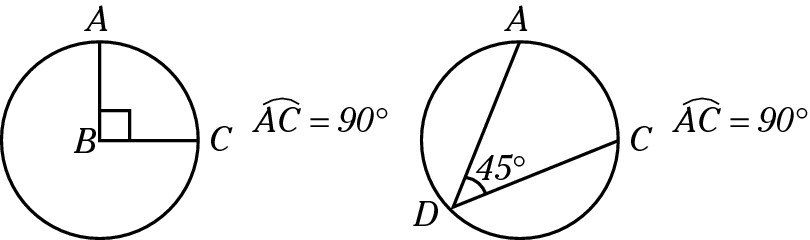

1. Find the circumference of the entire circle.
2. Put the degree measure of the arc over 360 and then reduce the fraction.
3. Multiply the circumference by the fraction.
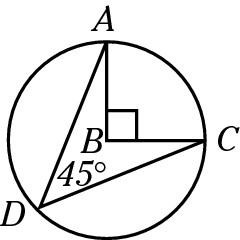
 Find the length of Arc AC.
Find the length of Arc AC.
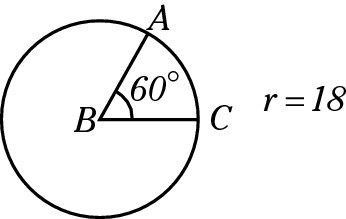
A 36π
B 27π
C 18π
D 12π
E 6π
Take the steps one at a time:
1. Find the circumference of the entire circle:
C = 2πr = 2(18)π = 36π
 Don’t multiply π out; answer choices usually leave it in that form.
Don’t multiply π out; answer choices usually leave it in that form.
2. Put the degree measure of the arc over 360.
The degree measure of the arc is the same as its central angle, 60 degrees:
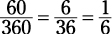
3. Multiply the circumference by the fraction:
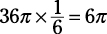
Correct answer: Choice (E).
Try another one. After you get the hang of arc problems, they’re actually kind of fun.
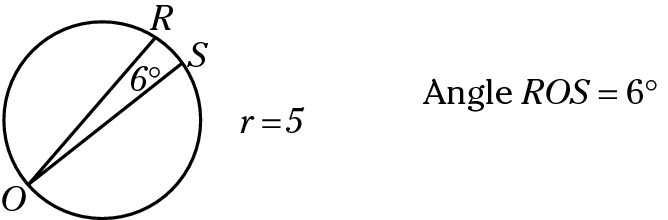
 Find the length of Arc RS in this figure.
Find the length of Arc RS in this figure.
A 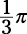
B π
C 3π
D 4π
E 12
1. Find the circumference of the entire circle:
C = 2πr = 2(5)π = 10π
2. Put the degree measure of the arc over 360.
Here, the inscribed angle is 6 degrees. Because an inscribed angle is 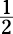 of the central
of the central
angle and 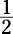 of its intercepted arc, the arc is 12 degrees:
of its intercepted arc, the arc is 12 degrees:
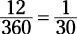
3. Multiply the circumference by the fraction:
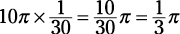
Correct answer: Choice (A).
Sectors
A sector is a portion of the area of a circle. The degree measure of a sector is the same as its central angle and twice its inscribed angle.
1. Find the area of the entire circle.
2. Put the degree measure of the sector over 360 and then reduce the fraction.
3. Multiply the area by the fraction.
Finding the area of a sector is very similar to finding the length of an arc. The only difference is in the first step. Whereas an arc is a part of the circumference of a circle, a sector is a part of the area of a circle. With that in mind, try your hand at a few sample sector problems:
 Find the area of Sector ABC.
Find the area of Sector ABC.
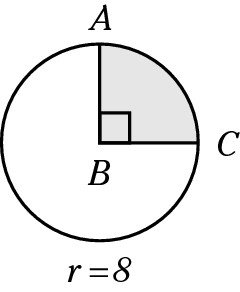
A 64π
B 36π
C 16π
D 12π
E 6π
Use the three steps listed previously:
1. Find the area of the entire circle.
A = πr2 = π × 82 = 64π
2. Put the degree measure of the sector over 360 and then reduce the fraction.
The sector is 90 degrees, the same as its central angle:
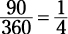
3. Multiply the area by the fraction.
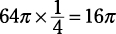
Correct answer: Choice (C).
 Find the area of Sector XYZ in this figure.
Find the area of Sector XYZ in this figure.
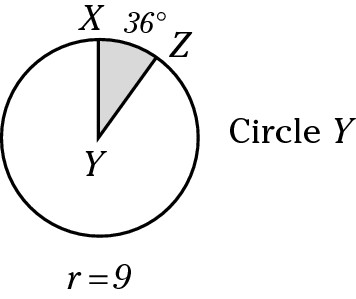
A 9.7π
B 8.1π
C 7.2π
D 6.3π
E 6π
1. Find the area of the entire circle.
A = πr2 = π × 92 = 81π
2. Put the degree measure of the sector over 360 and then reduce the fraction.
A sector has the same degree measure as its intercepted arc:
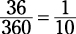
3. Multiply the area by the fraction.
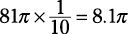
Correct answer: Choice (B).
Tackling shaded-area problems
A shaded-area problem presents two shapes with one overlapping the other but not completely covering it. The part of the shape underneath what you can see is the shaded area. Your job is to calculate the total shaded area.
 A circle of radius 4 inches is centered over an 8-inch square. Calculate the total shaded area.
A circle of radius 4 inches is centered over an 8-inch square. Calculate the total shaded area.
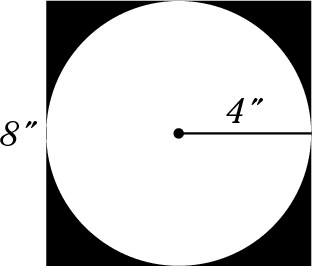
Shaded areas are often rather unusual shapes. Your first reaction may be that you can’t possibly find the area of that shape. Generally, you’re right, but you don’t have to find the area directly. Instead just find the areas of each shape (the one overlapping and the one underneath) and don’t worry about working the actual math.
1. Calculate the total area of the figure, which is the area of the square.
All sides of the square are 8 inches, so:
Area = 8 × 8 = 64
2. Calculate the area of the circle:
Area = πr2 = π × 42 = 16π
3. Subtract the area of the circle from the area of the square to determine the area of the shaded portion:
Area = 64 – 16π
Going 3D with Volume and Surface Area
You can easily calculate volume and total surface area for any three-dimensional shape that you encounter on the GRE. Fortunately, the GRE features only two such shapes: the rectangular solid (which includes the cube) and the cylinder. In the following sections, I give you the formulas and guidance you need to do so.
Calculating volume
Volume is how much you can fit inside a three-dimensional object and is always expressed in cubic units. The following sections explain how to calculate the volume of a cube, rectangular solid, a cylinder, and any polygon.
Volume = (area of base) × height
Cube = e3
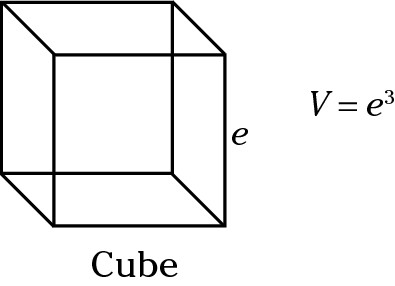
A cube is a three-dimensional square. Think of a die (one of a pair of dice). All of a cube’s dimensions are the same, that is, length = width = height. In a cube, these dimensions are called edges and are represented by the letter e. The volume of a cube is thus edge × edge × edge = edge3 = e3.
Rectangular solid = l × w × h
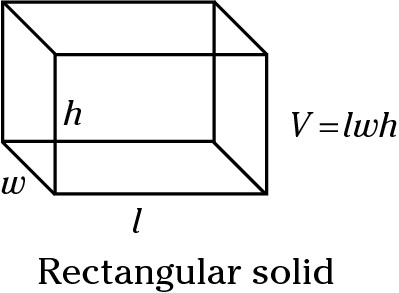
A rectangular solid is a box. The base of a box is a rectangle, which has an area of length × width. Multiply that by height to find volume: Volume = (area of the base) × height, or V = l × w × h.
Volume of a cylinder = πr2 × h
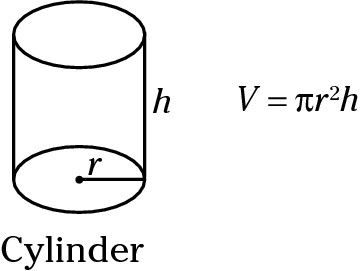
Think of a cylinder as a can of soup. The base of a cylinder is a circle. The area of a circle is πr2. Multiply that by the height of the cylinder to get (area of the base) × height = (πr2) × height. Note that the top and bottom of a cylinder are identical circles. If you know the radius of either the top base or the bottom base, you can find the area of the circle.
Calculating total surface area
Surface area is the measure of the exposed surface of an object — completely around it and its top and bottom. Total surface area (TSA), logically enough, is the sum of the areas of all the surfaces of the figure. The following sections provide formulas for calculating the surface area of several different solids.
Cube = 6e2
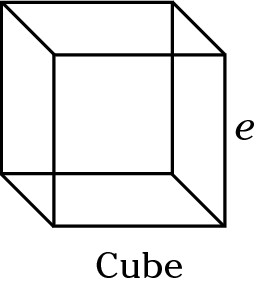
A cube has six identical faces, and each face is a square. The area of a square is side2. Here, that’s called edge2. If one face is edge2, then the total surface area is 6 × edge2, or 6e2.
Rectangular solid = 2(lw) + 2(wh) + 2(hl)
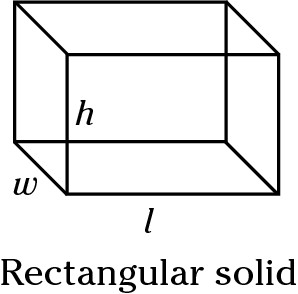
A rectangular solid is a box. You need to find the area of each of the six surfaces. The bottom and top each has the area of (length × width). The area of the left side and right side each is equal to (width × height). The front side and the back side each has the area of (height × length). Together, they total 2(lw) + 2(wh) + 2(hl) or 2(lw + wh + hl).
Cylinder = Circumference × height + 2(πr2)
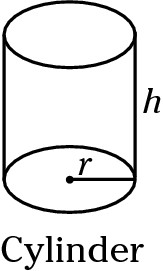
The TSA of a cylinder is definitely the most difficult TSA to figure out. Think of it as pulling the label off a can, flattening it out, finding its area, and then adding that to the area of the top and bottom lids.
The label is a rectangle. Its length is the circumference of the circle. Its height is the height of the object. And area of a rectangle is l × w.
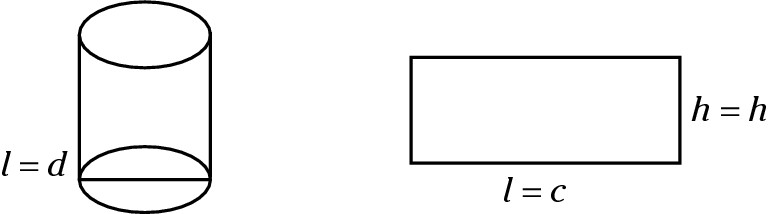
You also need to find the area of the top and bottom of the cylinder. Because both the top and bottom are circles, their TSA is 2(πr2). Finally, add everything together:
area of label + 2(area top or bottom) = TSA
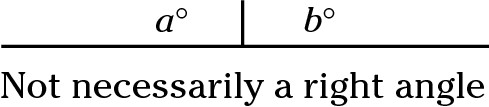
 Don’t put blind trust in drawings that accompany questions. For example, an image may appear to contain a right angle, but if the right-angle box is missing and the question doesn’t specify it as a right angle, you can’t assume it is. In addition, images may not be drawn to scale, so when a question presents an image, look for numbers in the question or on the figure that specify dimensions. Two sides of a triangle, for example, may appear to be equal when one is actually slightly longer than the other.
Don’t put blind trust in drawings that accompany questions. For example, an image may appear to contain a right angle, but if the right-angle box is missing and the question doesn’t specify it as a right angle, you can’t assume it is. In addition, images may not be drawn to scale, so when a question presents an image, look for numbers in the question or on the figure that specify dimensions. Two sides of a triangle, for example, may appear to be equal when one is actually slightly longer than the other. 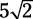 . Why? A square’s diagonal cuts the square into two isosceles right triangles (
. Why? A square’s diagonal cuts the square into two isosceles right triangles (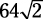 . What’s the diagonal of a square of side 12,984?
. What’s the diagonal of a square of side 12,984? 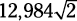 .
.