Chapter 11
Translating English into Math: Word Problem Strategies
In This Chapter
 Making sense of word problems
Making sense of word problems
 Calculating distance, rate, time, averages, interest, probability, and more
Calculating distance, rate, time, averages, interest, probability, and more
 Grasping set theory while grappling with Venn diagrams
Grasping set theory while grappling with Venn diagrams
 Determining the order of items with permutations and combinations
Determining the order of items with permutations and combinations
Being able to do calculations in math is necessary for scoring well on the Math sections of the GRE, but number-crunching alone isn’t enough. You also need to be able to translate a word problem from English into a mathematical expression.
Fortunately, the GRE uses several standard types of word problems, each of which you solve using one or more strategies. Recognize the type of problem you’re dealing with and choose the right strategy, and you’re well on your way to solving the problem.
This chapter introduces you to the various word problem types and reveals strategies for answering each type of question efficiently and accurately.
Working a Word Problem Step by Step
When you’re eye-to-eye with a word problem, knowing where to start is often the most daunting challenge. The key is to begin with what you know and work toward what you don’t know. You can solve almost all word problems by taking the following step-by-step approach:
1. Read the entire problem carefully.
A question may provide three values and then ask for the total or the average. You may not know until the very end of the question what it’s asking you to determine, so read the entire question.
2. Jot down all the values and units you know.
When you see all the values, what you need to do to solve the problem often reveals itself. Values are the clues you need to solve the mystery.
3. Identify the unknown variable — what the question is asking you to come up with.
 The unknown variable, x, is whatever the question asks. Look for words such as what is, how much, how many, how fast, at what price, and so on.
The unknown variable, x, is whatever the question asks. Look for words such as what is, how much, how many, how fast, at what price, and so on.
4. Construct the mathematical equation, plugging in all known values and the variable.
In most cases, the word problem is of a distinct type, and solving it requires the use of a special equation. The following sections bring you up to speed on the most common word problem types and their corresponding equations. With the equation, known values, and unknown variable in hand, you have everything you need to solve the problem.
5. Solve the equation.
When you have everything in place, do the math.
6. Plug in your choice to be sure.
Plug in the answer you chose and crunch the numbers to be sure it works, or at least use your common sense to gauge whether the answer seems reasonable.
Are We There Yet? Calculating Distance, Rate, and Time
You’re probably going to encounter at least one question on the GRE that deals with distance, rate, and time. The question typically provides two of the three values and asks for the third value; for example, the question may specify the distance and rate and ask for the time. To solve these types of questions, create a DRT (distance, rate, time) chart and start filling in values.
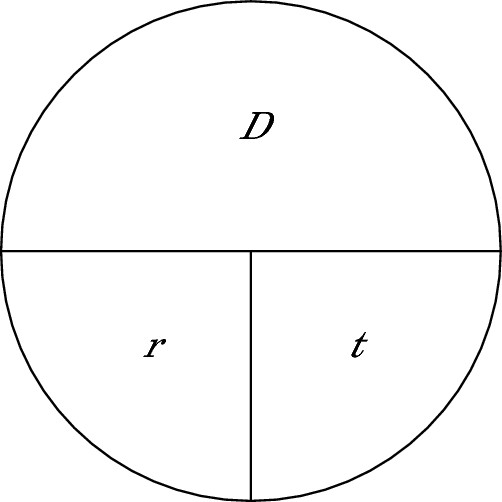
Cover up the letter for the value you don’t have, and this little tool reveals the equation for determining that value:
 Cover the D, and you see that D = rt.
Cover the D, and you see that D = rt.
 Cover the t, and you see that
Cover the t, and you see that 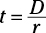 .
.
 Cover the r and you see that
Cover the r and you see that 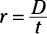 .
.
 Jennifer drives 40 miles an hour for two and a half hours. Her friend Ashley goes the same distance but drives at one and a half times Jennifer’s speed. How many minutes longer does Jennifer drive than Ashley?
Jennifer drives 40 miles an hour for two and a half hours. Her friend Ashley goes the same distance but drives at one and a half times Jennifer’s speed. How many minutes longer does Jennifer drive than Ashley?
Don’t start making intense formulas with x’s and y’s. Make a DRT chart instead. This chart lays out everything you know and what you need to know to answer the question:
|
Distance |
= |
Rate |
× |
Time |
Start by writing down the values you know, including the units of measurement. When you fill in the 40 miles per hour and 2.5 hours for Jennifer, you can calculate that she went 100 miles. Think of it this way: If she goes 40 miles per hour for one hour, that’s 40 miles.
For a second hour, she goes another 40 miles. In a half-hour, she goes 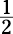 of 40, or 20 miles: 40 + 40 + 20 = 100 miles.
of 40, or 20 miles: 40 + 40 + 20 = 100 miles.
|
Distance |
= |
Rate |
× |
Time |
|
100 (Jennifer) |
40 mph |
2.5 hours |
Because Ashley drives the same distance, fill in 100 under distance for her. She goes one and a half times as fast, so she’s going 40 + 1.5(40) = 40 + 20 = 60 miles per hour. You know Ashley’s distance and rate, and you need to find the time.
|
Distance |
= |
Rate |
× |
Time |
|
100 (Ashley) |
60 mph |
100 minutes |
Now all you need to do is convert Jennifer’s 2.5-hour drive into minutes and subtract. One hour is 60 minutes. A second hour is another 60 minutes. A half-hour is 30 minutes. Add them together: 60 + 60 + 30 = 150 minutes. If Jennifer drives for 150 minutes and Ashley drives for 100 minutes, Jennifer drives 50 minutes more than Ashley.
|
Distance |
= |
Rate |
× |
Time |
|
100 (Jennifer) |
40 mph |
150 minutes |
||
|
100 (Ashley) |
60 mph |
100 minutes |
Figuring Averages
When it comes to averages, you can always do them the way your teacher taught you in the third grade: Add all the terms and then divide by the number of terms. First, add up all the terms:
5 + 11 + 17 + 23 + 29 = 85
Next, divide the total by the number of terms, which is 5:
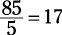
That’s the surefire method. It works in every case, regardless of what the numbers look like.
The following sections reveal shortcuts for calculating averages and show you how to tackle problems that are variations on the averages theme: missing-term average problems and weighted averages.
Taking shortcuts: Finding averages of evenly spaced or consecutive terms
 The average of a set containing an odd number of terms that are evenly spaced is equal to the middle term. For example, 2, 4, 6, 8, 10 has an average of 6.
The average of a set containing an odd number of terms that are evenly spaced is equal to the middle term. For example, 2, 4, 6, 8, 10 has an average of 6.
 A set containing an even number of evenly spaced terms is equal to the average of the
A set containing an even number of evenly spaced terms is equal to the average of the
two middle terms. For example, 2, 4, 6, 8 has an average of 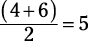 .
.
 The average of a set of evenly spaced terms is
The average of a set of evenly spaced terms is 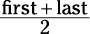 . For example, 2, 4, 6, 8, 10 has
. For example, 2, 4, 6, 8, 10 has
an average of 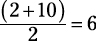 .
.
 Conversely, with evenly spaced terms, the sum of the first and last terms is equal to twice the average of the terms.
Conversely, with evenly spaced terms, the sum of the first and last terms is equal to twice the average of the terms.
 Find the average of these numbers:
Find the average of these numbers:
41, 50, 59, 68, 77, 86, 95
Don’t reach for your pencil. Instead, look and see that the terms are all nine units apart. Because the set contains an odd number of terms that are evenly spaced, the average is equal to the middle term: 68.
 Find the average of these numbers:
Find the average of these numbers:
3, 10, 17, 24, 31, 38, 45, 52
First, double-check that they’re evenly spaced. Here, the numbers are spaced by sevens. Next, look for the middle number . . . but wait! It doesn’t exist. You can, of course, identify the two central terms, 24 and 31, and find the middle between them. That works, but what a pain. Suppose you have 38 numbers. Making a mistake as to which terms are the central ones is easy with this many numbers. If you’re off just a little bit, you miss the question.
Instead, use the second rule: Just add the first and the last terms, which you can see at a
glance, and divide that sum by 2. In this case, 3 + 52 = 55, and 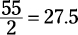 .
.
Note: Double-check your answer by using your common sense. Perhaps you made a silly mistake and got 45 for your answer. A quick glance at the numbers tells you that 45 isn’t in the middle and therefore can’t be the average.
This tip on averaging the first and last terms works for all evenly spaced terms. It doesn’t matter whether the series has a middle number, as in the first example, or no middle number, as in the second example. Go back to the first example:
32, 41, 50, 59, 68, 77, 86, 95, 104
Instead of finding the middle term, add the first and last terms and divide by 2, like this:
32 + 104 = 136, and 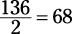 . Either way works.
. Either way works.
Solving missing-term average problems
A missing-term average problem is one that gives you the average and all but one of the values and asks for that missing value.
 A student takes seven exams. Her scores on the first six are 91, 89, 85, 92, 90, and 88. If her average on all seven exams is 90, what did she get on the seventh exam?
A student takes seven exams. Her scores on the first six are 91, 89, 85, 92, 90, and 88. If her average on all seven exams is 90, what did she get on the seventh exam?
To solve a problem like this, you can use the algebraic method or the over-and-under method.
Algebraic method
To solve a missing-term average problem, use algebra to find the unknown, as explained in Chapter 9. Start with the average equation, plug in a variable for the unknown value, and then solve for that variable:
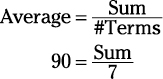
Because you don’t know the seventh term, call it x. Add the first six terms to get 535 plus x and then solve for x.
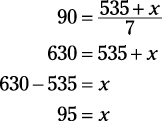
The seventh exam score was 95.
Over-and-under method
The over-and-under method for solving missing-term average problems is slightly more straightforward:
1. List the values and then jot down how much each value is over or under the target average.
The example problem tells you that the student’s first six scores are 91, 89, 85, 92, 90, and 88, and her average on all seven exams is 90. Find out how far each of the six scores is from 90. For example, 91 is 1 over 90, and 85 is 5 under 90. Do this for the rest of the scores, and here’s what you get:
Average = 90
91: +1
89: –1
85: –5
92: +2
90: 0
88: –2
You can toss the 90, because it’s equal to the target average.
2. Add the numbers showing the values over and under the target.
The +1 and –1 cancel each other out, and the +2 and –2 cancel each other out. You’re left with –5.
3. Use the sum from Step 2 to find out how far the last value needs to be over or under the target average.
The missing score needs to be +5 to make up for the –5. Therefore, the seventh test score must be 90 + 5 = 95.
 The shortcut, over-and-under way is quick and easy, but don’t forget to switch the sign on the sum of the over/under values. That is, if you decide that you’re minus five points going into the final exam, you need to be plus five points on that last exam to come out even. If you subtract five points from the average instead of adding them, you’ll probably arrive at one of the trap answers.
The shortcut, over-and-under way is quick and easy, but don’t forget to switch the sign on the sum of the over/under values. That is, if you decide that you’re minus five points going into the final exam, you need to be plus five points on that last exam to come out even. If you subtract five points from the average instead of adding them, you’ll probably arrive at one of the trap answers.
Try solving a missing-term average problem with the over-and-under method.
 A student takes seven exams. She gets an 88 average on all of them. Her first six scores are 89, 98, 90, 82, 88, and 87. What does she get on the seventh exam?
A student takes seven exams. She gets an 88 average on all of them. Her first six scores are 89, 98, 90, 82, 88, and 87. What does she get on the seventh exam?
Average = 88
89: +1
98: +10
90: +2
82: –6
88: 0
87: –1
Toss the 88. Now add the numbers that show how far the numbers are from the target average. The +1 and –1 cancel. Then you have 10 + 2 = 12 and –6, for a total of +6. So this student is 6 points above what she needs for the ultimate outcome. She can afford to lose 6 points on the final exam, or to be six points below the average. That gives her an 82.
You may be given only five out of seven scores and asked for the average of the missing two terms. Take the same approach as when you have one missing number and then divide by 2, because you have two missing numbers.
Here’s the algebraic way:
Average of seven exams: 85
Scores of the first five exams: 86, 79, 82, 85, 84
Find: The average score of each of the remaining exams
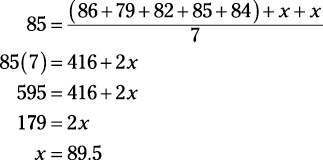
And here’s the over-and-under way to find the two missing numbers:
Average = 85
86: +1
79: –6
82: –3
85: 0
84: –1
Toss the 0. The +1 and –1 cancel each other out. You’re left with –9 for two exams, or –4.5 per exam. If you’re down four and a half points, you must gain those four and a half points on each of the two exams:
85 + 4.5 = 89.5
Working with weighted averages
A weighted average is one that takes into account statistical data, such as the number of students earning a score on a test or the number of employees earning a given salary. In a weighted average, some values count more than others.
To calculate a weighted average, multiply each value, such as a specific score or salary, by the number of occurrences of it, such as the number of students who got that score or the number of employees who earn that salary. Then, divide by the total occurrences, such as the total number of students or employees.

Find the average score for a student in a class of 15, given the following scores.
|
Number of Students |
Score |
|
5 |
120 |
|
10 |
90 |
To solve this problem, you can’t simply add 120 and 90 and divide by 2 because the scores aren’t evenly distributed among the students. Because 5 students got a 120, multiply 5 × 120 = 600. Do the same with the other score:
10 × 90 = 900
Now, add them all up:
600 + 900 = 1,500
You now have the total number of points that all the students earned. To figure out the average score, divide by the total number of students (5 + 10 = 15):
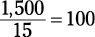
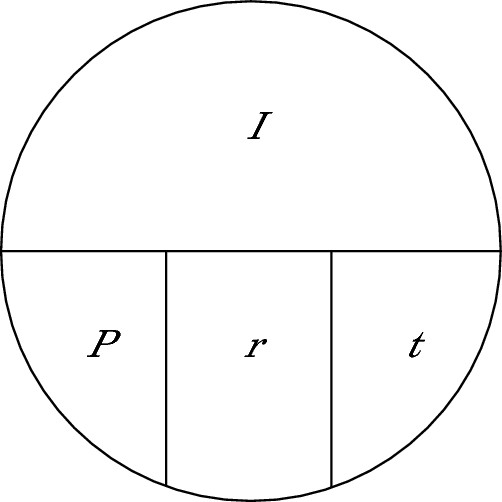
Calculating Simple Interest: I = Prt
Interest problems challenge you to calculate gains or losses on investments and the amount of interest paid on loans. To solve these problems, use this formula or some rendition of it: I = Prt.
I is interest, P is principal (the amount of money you start with), r is the interest rate, and t is time (always in years). An interest problem usually asks you how much interest someone earned on his or her investment, but the problem may ask how much interest someone paid on a loan.
 Janet invested $1,000 at 5% annual interest for one year. How much interest did she earn?
Janet invested $1,000 at 5% annual interest for one year. How much interest did she earn?
This is the simplest type of problem. Plug in the numbers and do the math:
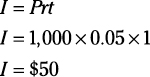
The answer choices may try to trap you with variations on a decimal place, making the
answers 5, 50, 500, and so on. You know that 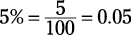 . Just be careful when multiplying and moving the decimal.
. Just be careful when multiplying and moving the decimal.
The GRE doesn’t throw many curves on interest problems. You won’t see something as technical as “calculate 5% annual interest compounded quarterly for 3 months.”
Cover up the letter for the value you don’t have, and this little tool reveals the equation for determining that value. Cover the I, for example, and you see that I = Prt. Cover the r, and
you see that 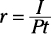 , and so on.
, and so on.
Working Out with Work Problems
Work problems typically tell you how long specific individuals would take to complete a task and then ask you how long they’d take to complete the task together, or some variation on that theme.
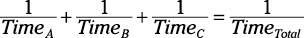
where TimeA is the time it takes the first person, TimeB is the time it takes the second person, and so on, and TimeTotal is the total time it takes them working together. You may keep adding people to the left side of the equation as needed.
 If Jonathan can paint a house in six days and David can paint a house in eight days, how many days does it take them to paint the house together?
If Jonathan can paint a house in six days and David can paint a house in eight days, how many days does it take them to paint the house together?
To solve this problem, plug in the numbers and do the math:
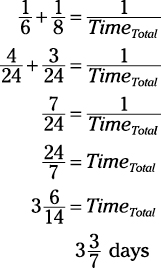
It would take the two working together 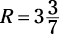 days to paint the house.
days to paint the house.
Double-check your answer by using your common sense. If you get an answer of 10, for example, you know you made a mistake somewhere because the two men working together should be able to do the job in less time than would either one working alone.
Mixing It Up with Mixture Problems
A mixture problem looks much more confusing than it really is. Plan to encounter two types of mixture problems: Those in which the items remain separate (when you mix peanuts and raisins, you still have peanuts and raisins), and those in which the two elements blend (these elements are usually concentrations of chemicals, like percents of salt in a mixture).
You can solve both types in the same general way, setting up tables that account for both the total mix and the component parts. Check out the separate mixture first.
 Carolyn wants to mix 40 pounds of beads selling for 30 cents a pound with a quantity of sequins selling for 80 cents a pound. She wants to pay 40 cents per pound for the final mix. How many pounds of sequins should she use?
Carolyn wants to mix 40 pounds of beads selling for 30 cents a pound with a quantity of sequins selling for 80 cents a pound. She wants to pay 40 cents per pound for the final mix. How many pounds of sequins should she use?
The hardest part for most test-takers is knowing where to begin. Stick to these steps to solve problems like this one:
1. Make a chart and start with the bare essentials — the labels for all the data you have to work with.
|
Pounds |
Price |
Total |
|
|
Beads |
|||
|
Sequins |
|||
|
Mixture |
2. Fill in the values that the test gives you.
Here, beads are 40 pounds at 30 cents a pound. Sequins are 80 cents per pound. You want the mixture to cost 40 cents a pound.
|
Pounds |
Price |
Total |
|
|
Beads |
40 |
$0.30 |
|
|
Sequins |
$0.80 |
||
|
Mixture |
$0.40 |
3. Use a variable to stand in for your unknown value.
You don’t know how many pounds of sequins you have, so that’s your variable, x. Now use a little logic to find the weight of the mixture. If you start with 40 pounds of beads and add this new unknown amount of sequins, x, you now have 40 + x pounds for the mixture.
|
Pounds |
Price |
Total |
|
|
Beads |
40 |
$0.30 |
|
|
Sequins |
x |
$0.80 |
|
|
Mixture |
40 + x |
$0.40 |
4. Multiply across the rows to fill in the total column.
|
Pounds |
Price |
Total |
|
|
Beads |
40 |
$0.30 |
$12.00 |
|
Sequins |
x |
$0.80 |
$0.80x |
|
Mixture |
40 + x |
$0.40 |
$0.40(40 + x) |
5. Solve for x.
In the Total column, the total cost of beads plus sequins equals the total cost of the mixture, so the equation looks like this:
$12.00 + $0.80x = $0.40(40 + x)
You know from the table that x is going to be in pounds, because it’s in the Pounds column, so drop the dollar signs for simplicity and do the math:
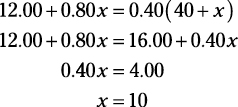
 In this case, you can drop the dollar signs and decimal points for simplicity, because the dollar amounts will cancel out on the two sides of the equation. The math then looks like this:
In this case, you can drop the dollar signs and decimal points for simplicity, because the dollar amounts will cancel out on the two sides of the equation. The math then looks like this:
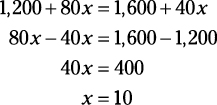
Careful! Keep in mind what x stands for. It represents the number of pounds of sequins, which is what the question asks for.
Go back and double-check the answer by plugging this value into the equation. You already know that Carolyn spent $12 on beads. If she buys 10 pounds of sequins for 80 cents, she spends $8, for a total of $20. She spends that $20 on 50 pounds: 2,000 ÷ 50 = 40. Easy as that.
A mixture question based on a concentration of chemicals works the same way. The only difference is that the total column represents amounts of substances (5 liters of a 40 percent saline solution contains 2 liters of salt) rather than cost.
 A chemistry student has one solution that’s 25% acid and another that’s 15% acid. Approximately how many liters of the 25% solution must be added to the 15% solution to make 10 liters of a solution that’s 20% acid?
A chemistry student has one solution that’s 25% acid and another that’s 15% acid. Approximately how many liters of the 25% solution must be added to the 15% solution to make 10 liters of a solution that’s 20% acid?
A 2.5
B 3.3
C 5.0
D 6.7
E 7.5
To answer this question, first create your table with the data you have:

Now create your equation and do the math to solve for x. The total 15% salt solution plus the total 25% salt solution equals the total 20% salt solution, so your equation looks like this:
0.25x + 0.15(10 – x) = 2
Now do the math:
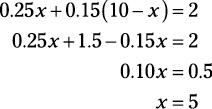
Sorting Out Sets and Groups
Set theory is a branch of mathematics that groups numbers, objects, or any items whatsoever into sets and describes the relationships between and among members of those sets. For example, you may group students by male and female and have members of each group form a subset for athletes. Of course, the math gets a little more involved than that, as the following sections reveal.
Set relationships: Dealing with unions, intersections, and subsets
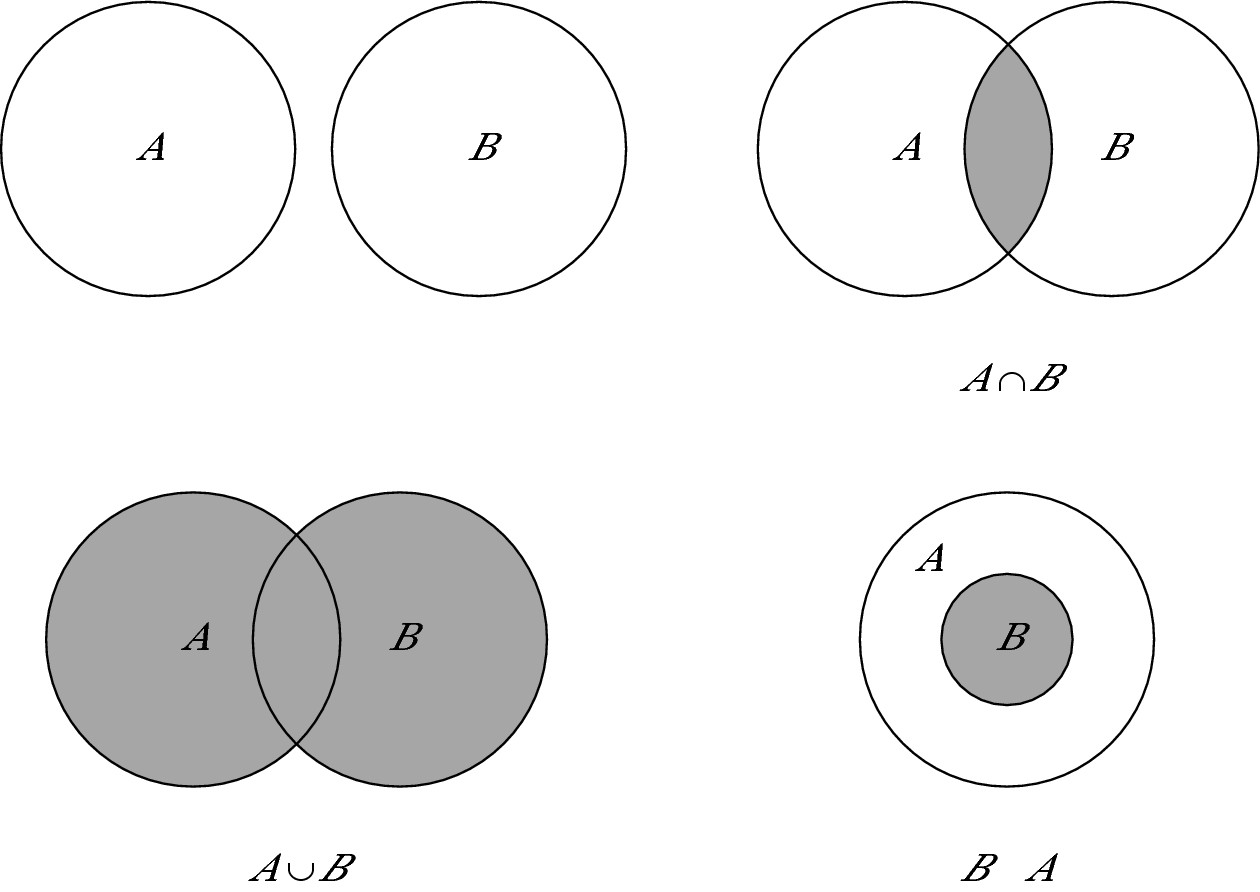
Sometimes sets overlap. Some or all of the members of one set belong to another set, and vice versa. To describe specifically how the sets overlap, set theory uses a u-shaped symbol: ,. The orientation of the symbol indicates a union, intersection, or subset relationship:
 Union: The union of two sets A and B, written as A , B, contains the members of both sets A and B. Suppose set A = {1, 2, 4, 6, 7, 9} and B = {0, 2, 3, 5, 8, 10}. Then A , B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Union: The union of two sets A and B, written as A , B, contains the members of both sets A and B. Suppose set A = {1, 2, 4, 6, 7, 9} and B = {0, 2, 3, 5, 8, 10}. Then A , B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
 Intersection: The intersection of two sets A and B, written as A + B, contains only members belonging to both sets. If set A = {1, 2, 4, 6, 7, 10} and B = {0, 2, 3, 5, 8, 10}, then A + B = {2, 10}.
Intersection: The intersection of two sets A and B, written as A + B, contains only members belonging to both sets. If set A = {1, 2, 4, 6, 7, 10} and B = {0, 2, 3, 5, 8, 10}, then A + B = {2, 10}.
 Subset: A subset, written as B , A, is a set within another set. All the members of the subset belong to both sets. If set A = {1, 2, 4, 6, 7, 10} and B = {1, 7, 10}, then B , A = {1, 7, 10}.
Subset: A subset, written as B , A, is a set within another set. All the members of the subset belong to both sets. If set A = {1, 2, 4, 6, 7, 10} and B = {1, 7, 10}, then B , A = {1, 7, 10}.
Math provides visual aids, called Venn diagrams, for understanding set theory and the relationships between members of different sets. A Venn diagram consists of a rectangle representing an abstract universal set along with usually two to three circles representing sets within the universal set. In most cases, the rectangle is omitted to simplify the illustration. The circles overlap in different ways to show the relationships between members of the sets. If you encounter a set question on the test and have trouble visualizing how the members of two sets relate to one another, consider drawing a Venn diagram on your scratch paper.
The following diagrams show no overlap, A , B, A + B, and B , A:
 What are the elements of Set C?
What are the elements of Set C?
A = {a, c, f, g, r}
B = {a, e, f, h, s, w}
C = A , B
A {a, f}
B 
C {a, b, c, e, f, g, h, r, s, w}
D {a, c, e, f, g, h, r, s, w}
E {A, B}
Set C is A union B, or the combination of all members of A and B without any doubles. Correct answer: Choice (D). If you chose Choice (A), you mistook the union symbol for the intersection symbol.
Set questions may include other mathematical concepts, including mean (same as average) or absolute value, as in the following example.

What is the average of the elements in Set L?
D = {1, 3, 6, 12, 18, 21}
F = {2, 3, 5, 12, 21, 22}
L = D + F
A 11
B 12
C 10
D 10.5
E 9.5
First list the elements in Set L. Set L equals the intersection of sets A and B, or the members that belong to both of those sets. Therefore, L = D + F = {3, 12, 21}. Find the average by adding the elements (3 + 12 + 21 = 36) and then dividing by the number of elements (36 ÷ 3 = 12). Correct answer: Choice (B). If you chose Choice (C), you determined the average for D , F. If you chose Choice (D), you determined the average for the total of all the values. If you chose Choices (A) or (E), you probably just took a wild guess.
Sorting out group questions
Group questions typically present you with two groups, describe a subgroup comprised of members from both groups or neither group, and ask how many members belong to that subgroup. These questions are similar to the set-relationships questions described in the previous section.
Group 1 + Group 2 + neither group – both groups = Total
 Of 200 employees, 60 took advantage of educational benefits, 145 participated in the company retirement program, and 40 participated in both programs. How many employees took advantage of neither program?
Of 200 employees, 60 took advantage of educational benefits, 145 participated in the company retirement program, and 40 participated in both programs. How many employees took advantage of neither program?
This group problem is about as straightforward as you can get. Jot down the known values and the unknown variable so you know what you have to work with:
Group 1: 60
Group 2: 145
Both groups: 40
Neither group: x
Total: 200
Plug the numbers into the group formula and do the math:
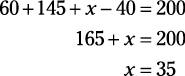
Solving Simple Probability Problems
Probability problems may seem a little intimidating at first. For example, a probability problem may ask your chances of drawing an ace, a king, and a queen from a deck of cards. Fortunately, three simple rules can help you solve nearly every probability problem tossed your way. In this section, I tell you how to find probability in general and how to find probabilities when multiple events occur.
Rule #1: Create a fraction
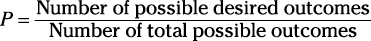
The denominator (the bottom part of the fraction) is usually the easier of the two parts to begin with. The denominator contains the total possible number of outcomes. For example, when you’re flipping a coin, two possible outcomes exist: heads or tails; that gives you a denominator of 2. When you’re tossing a die, six possible outcomes exist, giving you a denominator of 6. When you’re pulling a card out of a deck, 52 possible outcomes exist (because a full deck has 52 cards), giving you a denominator of 52. The denominator is the whole shebang — everything that’s possible.
The numerator shows the total possible number of the things you want. If you want to get heads when you toss a coin, exactly one side is heads, giving you a numerator of 1. The
probability of tossing heads, therefore, is 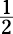 — one desired outcome over two possible
— one desired outcome over two possible
outcomes. Suppose you want to get a 5 when you toss a die. A die has exactly one 5 on it,
giving you a numerator of 1 and a denominator of 6. The probability of rolling a 5 is 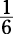 .
.
What is the probability of drawing a jack out of a deck of playing cards? The deck has 52 cards
(denominator) and four jacks (numerator), so the probability is 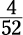 , which reduces to
, which reduces to 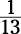 . The
. The
probability of drawing the jack of hearts, however, is only 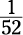 , because the deck contains only one jack in that suit.
, because the deck contains only one jack in that suit.
 A jar of marbles has 8 yellow marbles, 6 black marbles, and 12 white marbles. What is the probability of drawing out a black marble?
A jar of marbles has 8 yellow marbles, 6 black marbles, and 12 white marbles. What is the probability of drawing out a black marble?
You have 6 black marbles and 26 marbles total. The number of black marbles goes in the numerator, and the total number of marbles goes in the denominator resulting in a probability
of 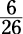 , or
, or 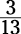 .
.
Rule #2: Multiply consecutive probabilities
A consecutive probability is the odds that a certain event will occur a specific number of times in a row; for example, if I flip a coin twice, the probability that it comes up heads both times. To solve a consecutive probability problem, find the probability of each event separately and then multiply them.
What’s the probability that you’ll get heads twice when you toss a coin twice? Find each probability separately and then multiply the two. The chance of tossing a coin the first time
and getting heads is 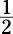 . The chance of tossing a coin the second time and getting heads is
. The chance of tossing a coin the second time and getting heads is 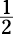 .
.
Multiply those consecutive probabilities:
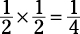
The chances of getting two heads are one out of four. Note that the probability would be the same whether you toss one coin twice or toss two coins at the same time.
 What’s the probability of tossing a die twice and getting a 5 on the first toss and a 6 on the second toss? Treat each toss separately.
What’s the probability of tossing a die twice and getting a 5 on the first toss and a 6 on the second toss? Treat each toss separately.
The probability of getting a 5 is 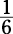 . The probability of getting a 6 is
. The probability of getting a 6 is 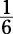 . Multiply consecutive probabilities:
. Multiply consecutive probabilities:
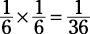
Again, the probability is the same whether you toss one die twice or two dice at the same time.
Rule #3: Add either/or probabilities on a single event
An either/or probability on a single event is one in which either of two outcomes may occur; for example, the probability that you reach into a bag containing 10 blue, 10 red, and 10 green marbles and pull out a blue or a red marble. To solve an either/or probability problem, find the probability of each event separately and then add them together.
What’s the probability of tossing a die once and getting either a 5 or a 6? Either outcome has a one in six chance of occurring:
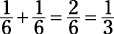
The probability of rolling either a 5 or a 6 on a single die roll is 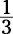 . Note that if you roll two
. Note that if you roll two
separate dice, the probability would be different, but the GRE won’t ask you to make this calculation.
Surveying Different Counting Methods
Counting certainly sounds easy enough, but when you’re counting the number of ways that several objects or events can be arranged, selected, or combined, counting becomes much more complex. The following sections explain some tricks to help you count these objects or events quickly and easily.
Putting the counting principle to work
Suppose you have five shirts, two pairs of pants, and two jackets. How many different outfits can you put together? To answer this question, apply the counting principle:
1. Make a space for each item that can change.
In this case, you have three spaces: one for shirts, one for pants, and one for jackets.
2. In each space, jot down the number of options.
You now have something like this:
|
Shirts |
Pants |
Jackets |
|
5 |
2 |
2 |
3. Multiply the numbers.
5 × 2 × 2 = 20 different outfits
Use the same technique to calculate the possible combinations you have when rolling two six-sided dice. Each die has 6 possible outcomes, so the total number of different ways the numbers on the dice can be combined are 6 × 6 = 36.
When order matters: Permutations
A permutation is a change in the arrangement of a given number of items or events. If the order in which items are arranged or in which events occur matters, you’re looking at a permutation problem. One of the simplest examples looks at the possible number of ways the three letters A, B, and C can be arranged (the possible number of permutations). The answer is six:
ABC BAC CAB
ACB BCA CBA
Based on the counting principle discussed in the previous section, you can figure this out without having to write out all the possible combinations. The first event (or letter in this case) has three possible outcomes (A, B, or C), the second event has two possible outcomes (the remaining two letters), and the third event has only one possible outcome (the last remaining letter):
|
1st Letter |
2nd Letter |
3rd Letter |
|
3 |
2 |
1 |
3 × 2 × 1 = 6
Whenever a question asks for the possible number of ways a certain number of objects may be arranged or events may occur, you may use the following formula:
(n)(n – 1)(n – 2)(n – 3) . . .
In which n represents the total number of items or events.
Mathematics uses the factorial as a convenient way to represent the product of integers up to and including a specific integer, so 3!, which stands for “ factorial,” is 3 × 2 × 1 = 6. Factorials play a key role in calculating possible permutations and combinations.
You can solve simple permutation problems using n! where n represents the number of objects to arrange or the order of events.
 Toby, Jill, Ashley, and Mark are racing their bicycles. How many different ways can they finish the race?
Toby, Jill, Ashley, and Mark are racing their bicycles. How many different ways can they finish the race?
Because four people are in the race, the different orders in which the four may finish is 4! = 4 × 3 × 2 × 1 = 24.
Permutation problems become more involved when you’re working with a subset of the entire number of objects or events, such as determining the possible number of ways three people out of 20 can finish a race first, second, and third or the total number of 4-digit sequences on a key pad that has 8 digits. To solve this type of permutation problem, use the following formula:
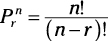
where P is the number of permutations you’re trying to determine, n is the total number of objects or events, and r is the subset of objects or events you’re working with at one time.
 Ten high school soccer teams are competing for a berth in the upcoming tournament. How many possible ways can the top three teams be ranked from first to third?
Ten high school soccer teams are competing for a berth in the upcoming tournament. How many possible ways can the top three teams be ranked from first to third?
Because order matters, this is a permutation problem. In this example, you have ten total teams, but you’re working with a subset of only three of those teams, so n = 10 and r = 3. Plug in the numbers and do the math:
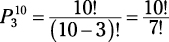
The numbers will always be simple enough to easily multiply. You can make it easier by reducing the fraction to its simplest terms first and then multiplying the remaining factors in the factorial:
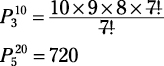
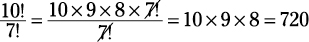
When order doesn’t matter: Combinations
A combination is a subset of objects or events in which order doesn’t matter; for example, choosing four pieces of fruit from a selection of 20 different types. If a question asks about choosing a number of items and the order in which items are arranged or events occur doesn’t matter, you’re looking at a combination problem.
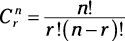
where C is the number of combinations you’re trying to determine, n is the number of objects or events, and r is the number of objects or events you’re choosing.
 From a group of ten colleagues, Sally must choose three to serve on a committee. How many possible combinations does she have to choose from?
From a group of ten colleagues, Sally must choose three to serve on a committee. How many possible combinations does she have to choose from?
Because the order doesn’t matter, this is a combination problem, so proceed as follows:
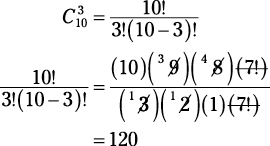
Using counting methods to solve probability problems
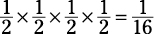
Now suppose you want to figure your odds of winning the lottery when you purchase a ticket. You pick two numbers out of 100. What are your odds that your two numbers will match the two winning lottery numbers?
Here, you’re choosing 2 out of 100 and the order doesn’t matter, so first use the combinations formula to determine the total possible two-number combinations:
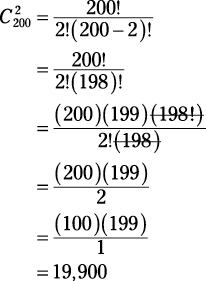
You have only one ticket, so your chances of winning are one out of that number, which is that number’s reciprocal:
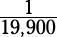
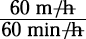 = 1 mile per minute. Therefore, going 100 miles takes her 100 minutes. Because
= 1 mile per minute. Therefore, going 100 miles takes her 100 minutes. Because 
 :
:  . If something is a member of a set, it’s tagged with the
. If something is a member of a set, it’s tagged with the 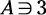 .
.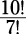 doesn’t equal
doesn’t equal 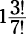 , although that may
, although that may