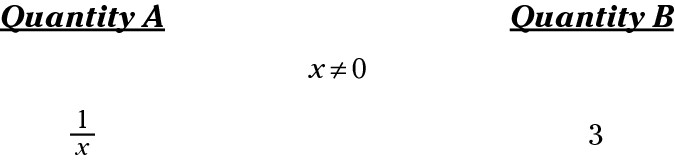Chapter 13
Comparing Quantities: They Report, You Decide Which Is Greater
In This Chapter
 Memorizing the elusive QC answer choices
Memorizing the elusive QC answer choices
 Knowing how to approach a QC problem
Knowing how to approach a QC problem
 Spotting and avoiding common traps
Spotting and avoiding common traps
 Putting it all together so you can work smarter, not harder
Putting it all together so you can work smarter, not harder
Almost one-third of the GRE math questions are Quantitative Comparisons (QC) with plenty of traps to trip you. QCs demand careful thought and insight to recognize and sidestep common traps; otherwise, you may stumble into some heavy duty and unnecessary math.
A QC question lists Quantity A and Quantity B. The quantities can be numbers, variables, equations, words, figures, and so on. Your job is to compare Quantity A to Quantity B and then determine whether one is greater than the other, they’re equal, or the relationship can’t be determined. The good news: This chapter gives you the lowdown on QC questions and how to solve them and also points out how to steer clear of common pitfalls.
The Answer Choices Are Always the Same: Memorize Them Now
With QC questions comprising about a third of each Math section, they consume a good chunk of your time allotment. To conserve time, memorize the QC answer choices prior to test day. Whatever the problem, the answer choices for QCs are always the same:
A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
Because the QC answer choices are always the same, memorizing them conserves precious time and energy during the test. As long as you know the choices, you don’t need to read and think about them each time.
A A is more.
B B is more.
C They’re the same.
D Need more information.
As Easy as π: Approaching QC Questions
The hardest part of answering a QC question is knowing where to begin. You can save considerable time and frustration by following this simple, three-step approach:
1. Solve for Quantity A.
Solve may mean solving an equation, talking through a word problem, or simply looking at what’s there. Here are some examples of what you may see in Quantity A:

2. Solve for Quantity B.
Again, solve can mean solving an equation, talking through a word problem, or just looking at the quantity, as you can see in the following examples:
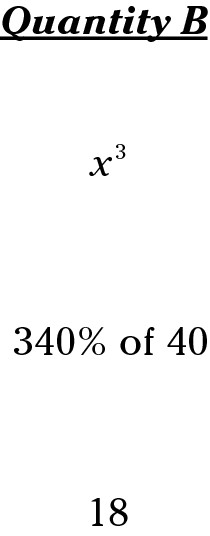
3. Compare the two quantities.
Sounds simple enough, right? But just wait until you see some of the cunning traps the GRE-developers build into the QCs.
Gotchas and Other Groaners: Tips, Traps, and Tricks
QC questions have so many tricks and traps that I provide a separate section for each one, with a few examples to illustrate how easily you can fall for the traps.
Remembering that equal appearances can be deceiving
If Quantity A and Quantity B appear to be equal at first glance, don’t fall for it — a trap is almost always involved. Check out the following examples:


Your gut reaction may be to choose Choice (C) because both quantities are equal. After all, wasn’t it drilled into your head in school that π equals 3.14? (If you’ve been out of school for quite a while, you may be very pleased with yourself for remembering the numerical value of π. Put the self-congratulations on hold; you’ve just fallen for a trap.) The value of π is only approximately 3.14. For convenience, your teachers and math books rounded π to two decimal places: 3.14. However, π is actually larger than that and continues as a nonrepeating, nonterminating decimal: 3.141592 . . . making π greater than 3.14 and Choice (A) the right choice. Correct answer: Choice (A).


You probably checked that the number of digits and decimal places are the same and chose Choice (C). But the answer is Choice (B). When you do the multiplication, Quantity A equals 22.32, and Quantity B equals 2,232. Big difference. The moral of the story? If your first reaction is that the problem is a no-brainer — that the answer is obviously, clearly, undoubtedly Choice (C) — then you’re hovering over a trap, so do the math to be sure. Correct answer: Choice (B).
Keeping an eye out for scale
If a figure in a QC problem isn’t drawn to scale, the answer is often Choice (D). How can you tell? Some figures may contain the guidance “Note: Figure not drawn to scale” below the picture, but don’t rely on the test-makers to offer this guidance. Instead, use your skills to gather information, such as line lengths or angle measurements, that enable you to answer the question. If those details are missing, you often can’t determine the relationship between the quantities and must choose Choice (D). Also, avoid the temptation to eyeball figures to arrive at your answer. If you don’t have a clue about how to gather the necessary information, use eyeballing only as a last resort.


Sure, x and y each appear to be 45 degrees, but because the figure isn’t drawn to scale, you can’t use it to estimate. You can’t look at the figure and deduce that x and y are equal. Yes, x and y add up to 90 degrees. That’s because angles along a straight line add up to 180 degrees, and you already have a right angle (the tiny box): 180 – 90 = 90. But you don’t know how much of the 90 is x and how much is y. Are they 45 and 45? 60 and 30? The figure isn’t to scale, so any of those values may be correct. Because you don’t have enough information to compare the quantities, go with Choice (D). Correct answer: Choice (D).

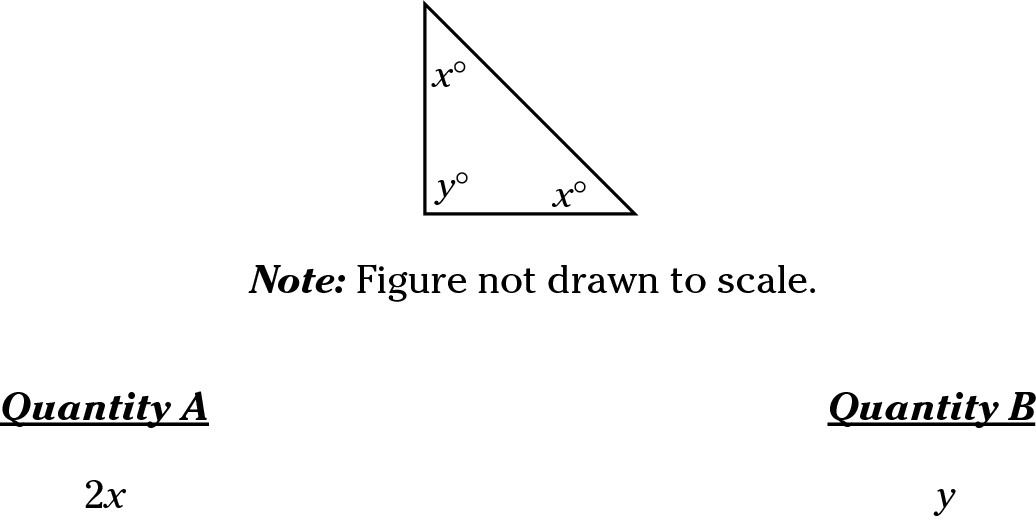
This QC question is an example of a classic Choice (D) answer. Yes, the figure appears to be an isosceles right triangle. You know that the two x’s are equal and that the angles in a triangle add up to 180 degrees. But no one said that Angle y is 90 degrees. It certainly looks like 90 degrees, but without having 90° specified or the tiny box that marks a 90-degree angle, you can’t be sure. Remember: Nothing is obvious; you can’t use the figure if it’s not drawn to scale. Because anything is possible, choose Choice (D). Correct answer: Choice (D).
Avoiding distraction from a pretty picture
The GRE may provide pictures (figures) to assist you in visualizing what the question is asking, but they may also use these pictures as traps. These drawings are never to scale. The GRE is challenging your grasp of the concept, not your ability to eyeball the lines and angles.
Two types of drawings are always to scale: the data graph or table and the coordinate grid (with x and y axes). (More on these drawings in Chapters 12 and 9, respectively.) Other than that, if the GRE doesn’t tell you the shape is a square, you can’t assume the angles are 90 degrees or the sides are equal.

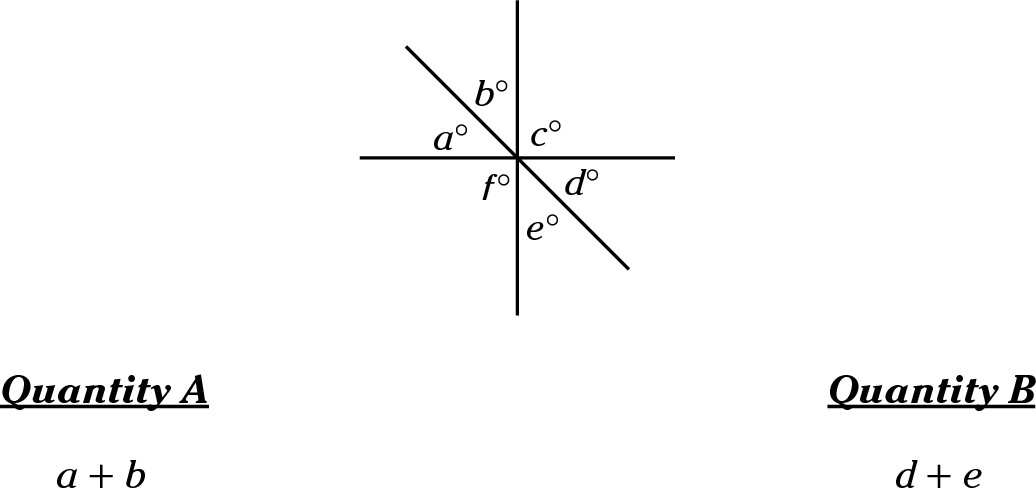
Angle a is a vertical angle to Angle d, meaning they’re opposite and of equal measure. Angle b is a vertical angle to Angle e, meaning they’re opposite and of equal measure. These are true regardless of whether the drawing is to scale. Because each part of Quantity A is equal to its counterpart in Quantity B, both quantities are equal. Correct answer: Choice (C).

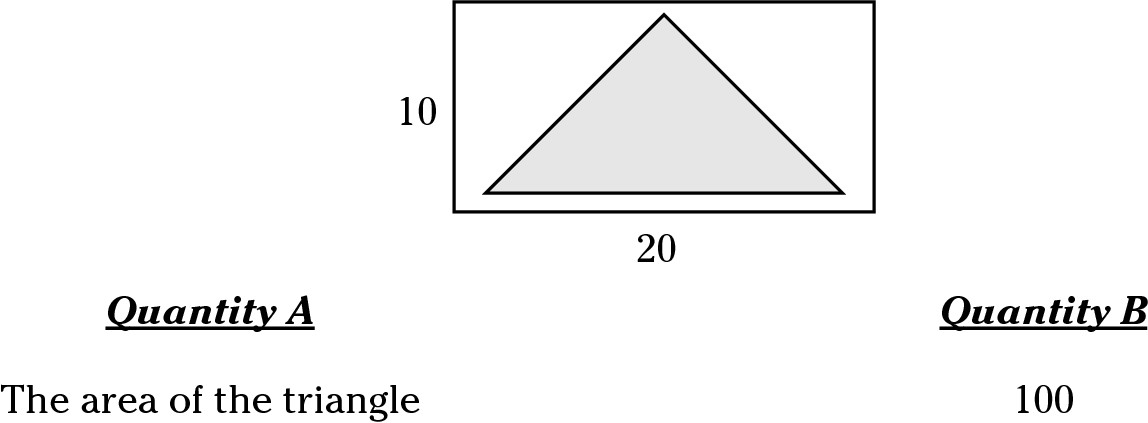
Fight the temptation to choose Choice (D) automatically just because you don’t have numbers for the lengths of the sides of the triangle. Though not drawn to scale, you can still estimate what you need to answer the question and compare the quantities.
The formula for the area of a triangle is 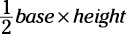 . What’s the base? You don’t know,
. What’s the base? You don’t know,
but you do know that it’s less than the base of the rectangle because the sides of the triangle don’t extend all the way to the sides of the rectangle. Just call it less than 20. What’s the height? You don’t know that either, but you do know that it’s less than 10 because the top and bottom of the triangle don’t touch the top and bottom of the rectangle. Call it less than 10. Multiply less than 10 × less than 20 to get less than 200. Half of less than 200 is less than 100. Because less than 100 is smaller than 100, choose Choice (B). Correct answer: Choice (B).
Canceling out identical quantities
Canceling quantities that are identical is like clearing the decks or simplifying the picture so you can more easily compare the two quantities. After all, a QC problem is like a balance: If something is the same on one side as on the other, it doesn’t affect the balance, so you can ignore it. Be careful that you cancel only identical terms though. For example, you can’t use –5 to cancel 5.


Cancel the x2 in both quantities, and you’re left with –21 and –35. Remember that a negative 21 is greater than a negative 35. Correct answer: Choice (A).
 a < 0
a < 0
b < 0

(a + b)2 = a2 + 2ab + b2 (a – b)2 = a2 – 2ab + b2
After foiling, you can cancel the identical terms a2 and b2 from both quantities. You’re left with +2ab in Quantity A and –2ab in Quantity B. You know that because a and b are both negative, ab is positive, so Quantity A is greater. Correct answer: Choice (A).
Weighing the quantities
Pretend the QC problem is a balance when comparing each part of Quantity A to its counterpart in Quantity B. If both parts of Quantity A are greater, or heavier, than both parts of Quantity B, Quantity A is greater.


Don’t even think about reaching for your pencil to work this problem through. Compare
each part of Quantity A to its counterpart in Quantity B. Which is greater: 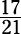 or
or 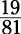 ? Reason
? Reason
that 17 is more than half of 21, whereas 19 is much less than half of 81. The same is true for the second pair of numbers. You know that 47 is more than half of 80; in contrast, 23 is less than half of 97. Because both parts of Quantity A are greater than both parts of Quantity B, Choice (A) is the answer. No muss, no fuss. Correct answer: Choice (A).
The point of the question is to recognize and use the test-makers’ hidden tricks so you can work smarter, not revert to a basic arithmetic, pull-out-your-pencil-type problem. Once in a while, you have to do the math, but not often.
Plugging in the Sacred Six
Here’s the best tip you’re likely to get outside a racetrack: Whenever you have variables,
plug in the Sacred Six: 1, 2, 0, –1, –2, and 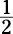 , specifically in that order. These numbers cover
, specifically in that order. These numbers cover
most of the contingencies: positive, negative, zero, odd, even, fraction, and 1, which has special properties. Memorize these numbers and throw them into a problem whenever possible. Note: This tip works even if an equation contains more than one variable.


The trap answer is Choice (B). At first glance, a number to the fourth power seems greater than the same number squared. (Two x’s in one problem always have the same value at one time, even in Quantities A and B. That is, if x is 5 in Quantity A, it’s also 5 in Quantity B. Always. No exceptions.)
Unfortunately, obvious answers are usually wrong answers. Play the “what if” game: What if x = 1? Then the two quantities are alike, and Choice (C) prevails. What if x = 2? Then Quantity A = 4 and Quantity B = 16, and the answer is Choice (B). Therefore, the answer can be Choices (C) or (B), depending on what you plug in. Using the Sacred Six removes any doubt that the answer is Choice (D). Correct answer: Choice (D).

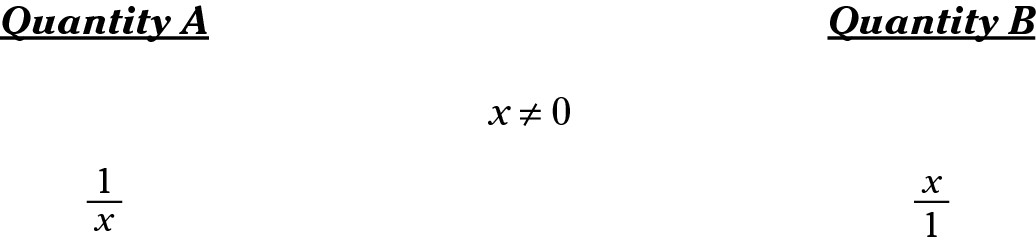
Again, Choice (B) is the trap answer. Most people think that Quantity A comes out to be a fraction of less than 1. It may, or it may not. If x were less than 1, then Quantity A would be greater than 1.
Play the “what if” game again. What if 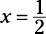 ? Then Quantity A is greater. What if x = 2?
? Then Quantity A is greater. What if x = 2?
Then Quantity B is greater. Because you can make either Quantity A or B greater, choose Choice (D). Correct answer: Choice (D).
On the real exam, you’d stop here, but for now, plug in a few more numbers to see what else may happen. You can’t plug in 0 because the problem tells you that x isn’t equal to 0 (division by 0 is undefined). What if x = –1? Then Quantity A is –1 and Quantity B is –1; they’re equal.
What if x = –2? Then Quantity A = 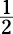 and Quantity B = –2; now Quantity A is bigger. You’ve seen
and Quantity B = –2; now Quantity A is bigger. You’ve seen
all the possibilities at this point: Quantity A can be bigger, Quantity B can be bigger, or the two quantities can be the same.
Throwing down a hundred
If a question deals with dollars or percentages, plug in 100 to make it an easier number. Any way to make the question easier is good.

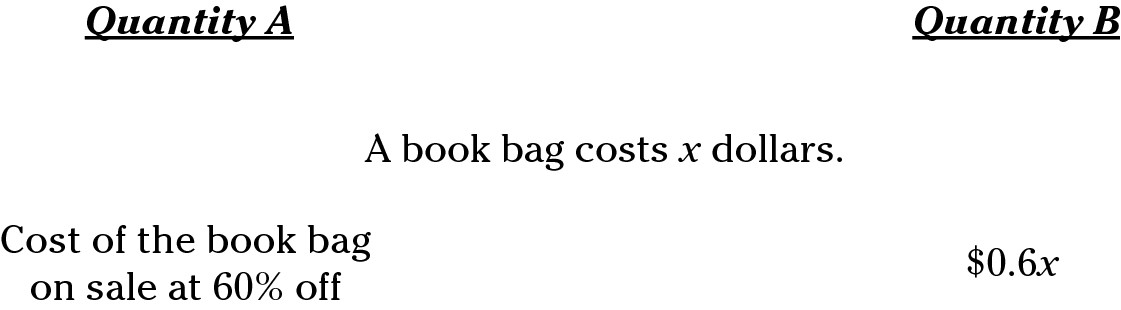
If you make x $100, you can easily determine that 60% of 100 is 60; subtract 100 – 60, and you get 40. In Quantity B, 0.6(100) = 60. The answer is Choice (B). This type of problem is easy to miss because of carelessness. Many people choose Choice (C) automatically. (Of course, if you read the earlier “Remembering that equal appearances can be deceiving” section, you know that if the quantities appear equal, you’re probably looking at a trap.) To improve your QC-problem-solving success, slow down, plug in 100, and do the math. Correct answer: Choice (B).


Gotcha! I tossed in this one to remind you that this chapter features tips, not rules, and you should never sacrifice common sense in favor of a tip. Sure, if you plug in 100 for x dollars, you know that the interest is $6 and Choice (B) is the answer. But what if x = $1,000,000? Then Quantity A is significantly larger. Although plugging in 100 often works, it won’t always work (like any shortcut, it’s not infallible), which is why you approach these questions critically. Correct answer: Choice (D).
Inserting variety when working with multiple variables
Some questions may provide you with multiple variables, such as the following:
a > b > c or x < y < z
In questions such as these, plug in consecutive terms first and then nonconsecutive terms. If you need to plug in numbers for two or three variables, first plug in the numbers all in a row: 1, 2, and 3. Then try plugging in numbers that aren’t in a row: 1, 5, and 7. Sometimes the spacing between the numbers makes a difference.

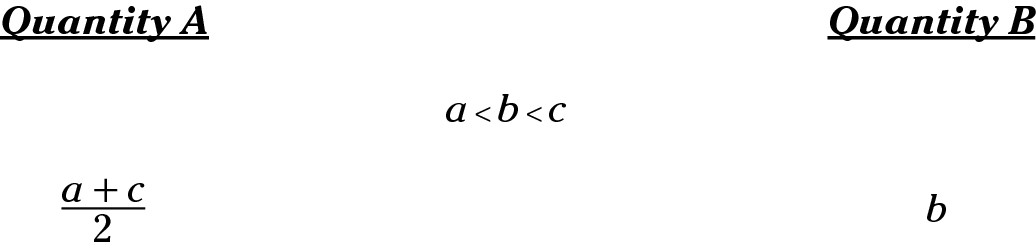
The normal response is to plug in consecutive numbers: 1, 2, and 3. If you do that, Quantity A is 1 + 3, or 4, divided by 2 = 2. In Quantity B, b is 2. The quantities are equal — a bright red warning flag. Remember that equal-looking quantities are often a trap, so double-check your work.
Plug in numbers that are farther apart: 2, 5, and 200. Now Quantity A is 2 + 200 = 202, divided by 2 = 101. In Quantity B, b is 5. Now the answer is Choice (A). If the answer changes based on which values you plug in for the variables, choose Choice (D). Correct answer: Choice (D).

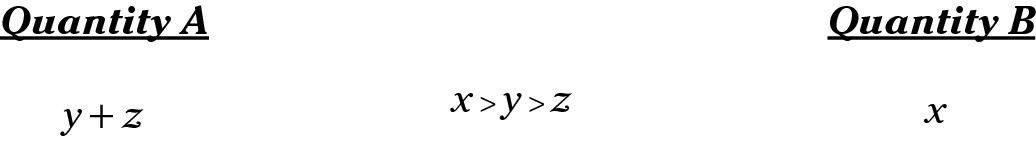
The immediate trap answer is Choice (C), but because x, y, and z can be anything, the right answer is Choice (D). If you plug in 3, 2, and 1, y + z = 2 + 1 = 3. Because x = 3, the quantities are equal. But when you plug in very different numbers, 100, 2, and 1, now, y + z = 2 + 1 = 3. But x = 100; Quantity B is larger. The answer changes depending on what you plug in, making Choice (D) the correct answer. Correct answer: Choice (D).
Deciding On Your Own: Quantitative Comparison Practice Questions
Here are some more QC practice questions in case you need a little extra work with these types of problems.
1. 4 < x < 5

A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
If x is less than 5, then x3 must be less than 125. Correct answer: Choice (B).
2.

A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
Remember that 25–4 can also be expressed as (25)–4, which becomes (52)–4 and then 5–8. Correct answer: Choice (C).
3. x and y are integers

A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
If x and y are positive integers, the correct answer would be Choice (A). If they’re negative, then the correct answer would be Choice (B). If they’re equal to zero, which is an integer, the correct answer would be Choice (C). Because you don’t know, the relationship can’t be determined. Correct answer: Choice (D).
4. The lengths of two sides of a certain triangle are 12 and 20.

A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
Because the length of the third side of any triangle must be less than the sum of the lengths of the other two sides, the third side of this triangle must be less than 32. Correct answer: Choice (B).
5. x > 0

A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
If x is an integer, then any value squared would be more than 0.5. However, because x could be a decimal, such as 0.2, x2 would equal 0.04. Because you can’t assume that x is an integer, you can’t tell which value is higher. Correct answer: Choice (D).
6. A circle has a radius of 1.

A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
The circumference of a circle is 2πr, making the circumference of this circle 2π. If π were equal to 3.14, then the answer would be Choice (C). However, the value of π is slightly higher, closer to 3.1416. You don’t have to know the exact value of π, but you do have to know that 3.14 is the value rounded down. Correct answer: Choice (A).
7. One of the angles of an isosceles triangle is 80°.

A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
If one of the angles is 80 degrees, then the other two angles could each be 50 degrees for a total angle measure of 180 degrees and a correct answer of Choice (C). However, the other two angles could also be 80 degrees and 20 degrees, bringing the angle total to 180 degrees for a correct answer of Choice (D). You don’t know which one is the case, so you can’t tell which quantity is greater. Correct answer: Choice (D).
8. At a certain factory, machines A and B have a maximum production capacity of p and q parts, respectively, where p < q < 100.
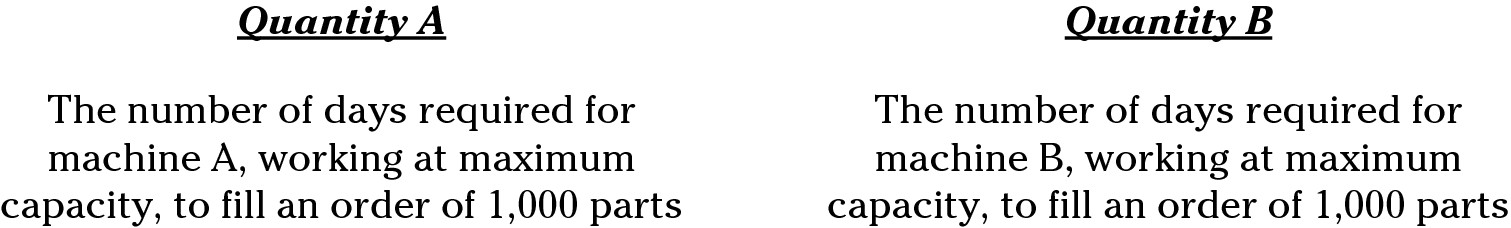
A Quantity A is greater.
B Quantity B is greater.
C The two quantities are equal.
D The relationship cannot be determined from the information given.
It’s easy to get lost in the description, picking numbers and trying math. Actually, after you get past the verbiage, this question is very simple. Pretend machine A produces 1 part per day and machine B produces 99 parts per day. Thus, machine A would take longer to produce 1,000 parts. Correct answer: Choice (A).

 Keep in mind that the following sections feature tips, not rules. A
Keep in mind that the following sections feature tips, not rules. A 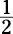 and 2 gives you
and 2 gives you 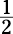 and 2 alone get the job done.
and 2 alone get the job done.