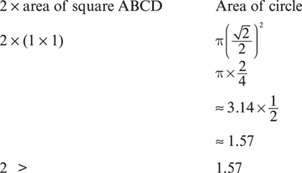Quantitative Comparison
Quantitative Comparison Strategies
This unique problem type appears on the SAT, the PSAT, and the GRE, among other exams. It tests your ability to compare two given quantities using your knowledge of mathematics.
Complex computation is not required. In fact, mathematical insight allows you to solve this type of problem more quickly than you can solve the more common math ability type of problem (see previous section).
Directions
In this section, you will be given two quantities—one in column A and one in column B. You are to determine a relationship between the two quantities and mark
A if the quantity in Column A is greater than the quantity in Column B
B if the quantity in Column B is greater than the quantity in Column A
C if the two quantities are equal
D if the comparison cannot be determined from the information given
Analysis
The purpose here is to make a comparison; therefore, exact answers are not always necessary. (Remember: In many cases, you can tell whether you're taller than someone without knowing that person's height. Comparisons such as this can be made with only partial information—just enough to compare.) Choice D is not a possible answer if there are values in each column, because you can always compare values.
If you get different relationships, depending on the values you choose for variables, then the answer is always Choice D. Notice that there are only four possible choices here. Never mark Choice E on your answer sheet for quantitative comparison questions.
Suggested Approach with Examples
Quantitative comparison questions emphasize shortcuts, insight, and quick techniques. Long and/or involved mathematical computations are unnecessary and are contrary to the purpose of this section.
Cancel Out Equal Amounts
Note that you can add, subtract, multiply, and divide both columns by the same value, and the relationship between them will not change. Exception: You should not multiply or divide each column by negative numbers, because then the relationship reverses. Squaring both columns is permissible, as long as each side is positive.

You should do the rest of this problem by inspection—Column B is obviously greater than Column A without doing any multiplication. Each number in Column B is larger than the corresponding number in Column A. You could've reached the correct answer by actually multiplying out each column, but you save valuable time if you don't. The correct answer is Choice B.
Make Partial Comparisons
Partial comparisons can be valuable in giving you insight into finding a comparison. If you can't simply make a complete comparison, look at each column part by part. For example:

Because finding a common denominator would be too time-consuming, you should first compare the first fraction in each column (a partial comparison). Notice that 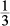 is greater than
is greater than 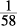 . Now compare the second fractions and notice that
. Now compare the second fractions and notice that 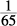 is less than
is less than 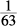 . Using some common sense and insight, if you start with a larger number and subtract a smaller number, it must be greater than starting with a smaller number and subtracting a larger number, as illustrated here:
. Using some common sense and insight, if you start with a larger number and subtract a smaller number, it must be greater than starting with a smaller number and subtracting a larger number, as illustrated here:
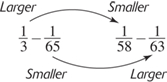
The correct answer is Choice A.
Keep Perspective
Always keep the column in perspective before starting any calculations. Take a good look at the value in each column before starting to work on one column. For example:

After looking at each column—note that the answer cannot be Choice D because there are values in each column—compute the value on the left: 72 = 49. There is no need to take 2 out to the 8th power. Just do as little as necessary: 22 = 4, 23 = 8, 24 = 16, 25 = 32. Stop. You can tell now that 28 is much greater than 49. The correct answer is Choice B. Approximating can also be valuable while remembering to keep the columns in perspective.
Plug In 0, 1, –1
If a problem involves variables (without an equation), substitute in the numbers 0, 1, and –1. Then try 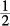 , and 2 if necessary. Using 0, 1, and –1 will often tip off the answer. For example:
, and 2 if necessary. Using 0, 1, and –1 will often tip off the answer. For example:

Substituting 0 for a and 0 for b gives

Using these values for a and b gives the answer: Choice C. But anytime you multiply two numbers, it isn't the same as when you add them, so try some other values.
Substituting 1 for a and –1 for b gives

and the answer is now Choice A.
Anytime you get more than one comparison (different relationships), depending on the values chosen, the correct answer must be Choice D (the relationship cannot be determined). Notice that if you had substituted the values a = 4 and b = 5, or a = 6 and b = 7, or a = 7 and b = 9, and so on, you would repeatedly have gotten Choice B and might have chosen the incorrect answer.
Simplify
Often, simplifying one or both columns can make an answer evident. For example:

Using the distributive property on Column A to simplify, gives ab and ac; therefore, the columns are equal.
Look for a Simple Way
Sometimes you can solve for a column in one step, without solving and substituting. If you have to solve an equation or equations to give the columns values, take a second and see if there is a very simple way to get an answer before going through all the steps. For example:
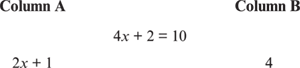
Hopefully, you would spot that the easiest way to solve for 2x + 1 is directly by dividing 4x + 2 = 10 by 2, leaving 2x + 1 = 5.
Therefore,
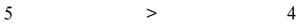
Solving for x first in the equation, and then substituting, would also have worked, but it would have been more time-consuming. The correct answer is Choice A.
Mark Diagrams
Marking diagrams can be very helpful for giving insight into a problem. Remember that figures and diagrams are meant for positional information only. Just because something looks larger isn't enough reason to choose an answer. For example:
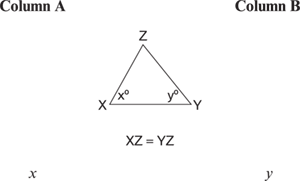
Even though x appears larger, this isn't enough. Mark in the diagrams as shown.
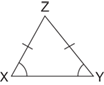
Notice that you should mark things of equal measure with the same markings, and because angles opposite equal sides in a triangle are equal, x = y. The correct answer is Choice C.
Use Easier Numbers
If you're given information that's unfamiliar to you and difficult to work with, change the number slightly (but remember what you've changed) to something easier to work with. For example:
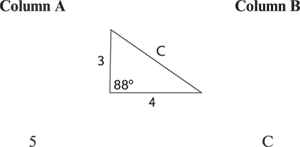
Since the 88° shown in the figure is unfamiliar to work with, change it to 90° for now, so that you may use the Pythagorean theorem to solve for c.
Solving for c:
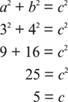
But because you used 90° instead of 88°, you should realize that the side opposite the 88° will be slightly smaller or less than 5. The correct answer is then Choice A, 5 > c. (You may have noticed the 3-4-5 triangle relationship and not needed the Pythagorean theorem.)
A Patterned Plan of Attack

Quantitative Comparison Practice
Directions
In this section, you will be given two quantities—one in Column A and one in Column B. You are to determine a relationship between the two quantities and mark
(A) if the quantity in Column A is greater than the quantity in Column B
(B) if the quantity in Column B is greater than the quantity in Column A
(C) if the quantities are equal
(D) if the comparison cannot be determined from the information given
Common information:
Information centered above both columns refers to one or both columns.
All numbers used are real numbers.
Figures are intended to provide useful positional information, but they are not necessarily drawn to scale and should not be used to estimate sizes by measurement.
Lines that appear straight can be assumed to be straight.
Arithmetic and Data Analysis
Questions


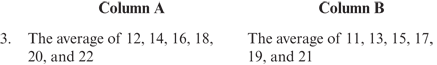


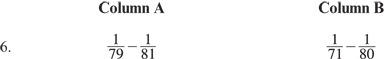

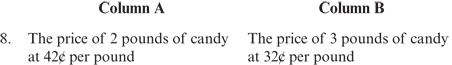
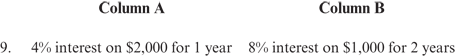

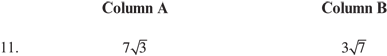
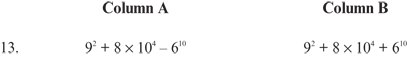
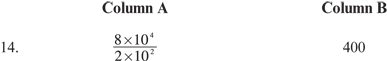

Algebra
Questions

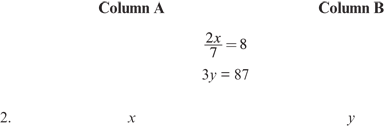





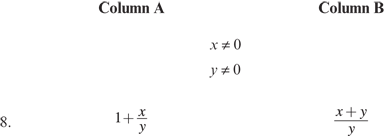
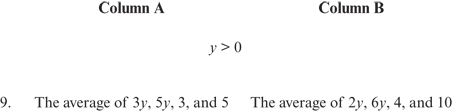
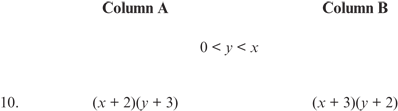

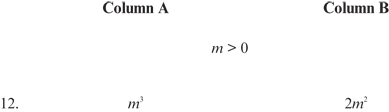
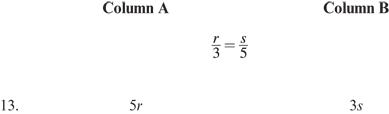
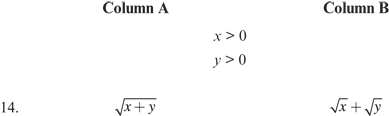
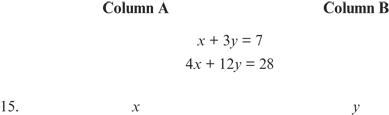
Geometry
Questions
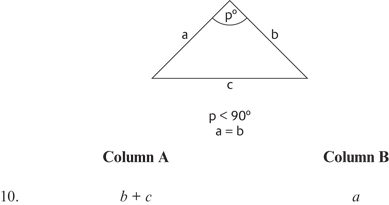
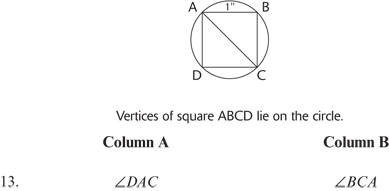
Question 1 refers to the following diagram.



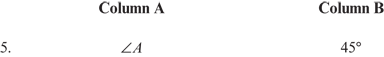

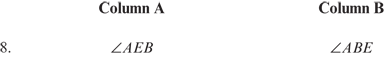
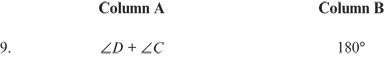
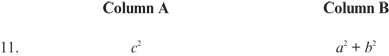
Answer Key for Quantitative Comparison Practice
The first heading in parentheses following each answer will direct you to the complete explanation for that specific problem. Read this explanation first. The other headings in parentheses refer to the suggested basic review section.
Arithmetic and Data Analysis
1. B (Explanation; Multiplying Fractions)
2. A (Explanation; Multiplying Fractions, Changing Decimals to Fractions)
3. A (Explanation; Mean)
4. A (Explanation; Motion)
5. A (Explanation; Changing Percents to Decimals)
6. B (Explanation; Adding and Subtracting Fractions)
7. A (Explanation; Finding Percent Increase or Percent Decrease)
8. B (Explanation)
9. B (Explanation; Simple Interest)
10. A (Explanation; Powers and Exponents)
11. A (Explanation; Simplifying Square Roots)
12. B (Explanation; Number Lines)
13. B (Explanation; Order of Operations)
14. C (Explanation; Division in Scientific Notation)
15. C (Explanation; Probability)
Algebra
1. A (Explanation; Evaluating Expressions)
2. B (Explanation; Solving Equations)
3. D (Explanation; Literal Equations, Solving Inequalities)
4. B (Explanation; Evaluating Expressions)
5. C (Explanation; Subtraction of Signed Numbers)
6. D (Explanation; Evaluating Expressions, Multiplying Monomials)
7. D (Explanation; Evaluating Expressions)
8. C (Explanation; Adding or Subtracting Algebraic Fractions)
9. B (Explanation; Adding and Subtracting Monomials, Multiplying Monomials)
10. A (Explanation; Evaluating Expressions, Dividing Monomials)
11. A (Explanation; Finding Percent of a Number)
12. D (Explanation; Evaluating Expressions)
13. C (Explanation; Solving Proportions for Value)
14. B (Explanation; Operations with Square Roots)
15. D (Explanation; Solving for Two Unknowns Systems of Equations)
Geometry
1. A (Explanation; Parallel Lines Cut by Transversal)
2. B (Explanation; Polygons, Circumference)
3. B (Explanation; Isosceles Right Triangles (45°-45°-90° Right Triangles), Circumference and Area of a Circle)
4. A (Explanation; Isosceles Right Triangles (45°-45°-90° Right Triangles), Arc)
5. C (Explanation; Isosceles Right Triangles (45°-45°-90° Right Triangles))
6. B (Explanation; Unequal Angles, Sum of the Interior Angles of a Polygon)
7. A (Explanation; Sum of the Interior Angles of a Polygon)
8. C (Explanation; Angles of an Equilateral Triangle)
9. A (Explanation; Sum of the Interior Angles of a Polygon)
10. A (Explanation; Adding Sides of a Triangle)
11. B (Explanation; Pythagorean Theorem)
12. A (Explanation; Adding Sides of a Triangle)
13. C (Explanation; Inscribed Angles)
14. C (Explanation; Isosceles Right Triangles (45°-45°-90° Right Triangles), Inscribed Angles)
15. A (Explanation; Perimeter and Area of Polygons, Circumference and Area of a Circle)
Quantitative Comparison Answers and Explanations
Arithmetic and Data Analysis
1. B Dividing out equal fractions from both sides (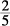 and
and 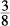 ), leaves Column A with
), leaves Column A with 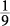 and Column B with
and Column B with 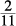 . Cross-multiply up:
. Cross-multiply up:

Since the larger product is always over the larger fraction, Column B is greater.
2. A Change the decimals in Column B to fractions:
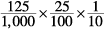
and reduce to the simplest form, and you get this comparison:
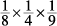

Canceling out the 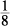 and
and 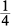 from each side leaves
from each side leaves
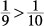
3. A The fastest way to determine which average is greater is to notice that each of the numbers in Column A is one larger than its corresponding number in Column B. Therefore, Column A's average must be greater than Column B's average.
4. A To find the average speed of the car in miles per hour, multiply 8 miles by 4, since 15 minutes is  of an hour:
of an hour:
8 × 4 = 32
32 miles per hour is the average speed and 32 > 30.
5. A Expressed as a percent, Column A equals 0.4%, which is greater than Column B.
6. B This problem is best solved by inspection. Notice that the values in Column A are very close together; therefore, their difference would be very small. Column B's values are farther apart, having a greater difference.
7. A To find percent increase, use the following formula:
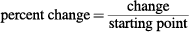 , then convert to a percent
, then convert to a percent
So,
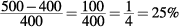 and 25% > 20%
and 25% > 20%
8. B Column A equals two times 42¢, or 84¢. Column B equals three times 32¢, or 96¢. Therefore, Column B is greater.
9. B The interest in Column A equals $2,000 times 0.04 times 1 year, or $80. The interest in Column B equals $1,000 times 0.08 times 2 years, or $160. Therefore, Column B is greater.
10. A 95 is 9 × 94, so if 94 is subtracted from 95, the remainder is obviously much greater than 94. Here is an alternate method:
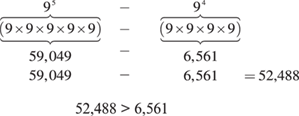
11. A The fastest and most accurate way to compare two terms, each of which contains a square root, is to change each term to a single term under a radical. For example,
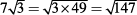
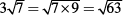
Since 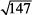 is greater than
is greater than 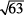 , Column A is greater.
, Column A is greater.
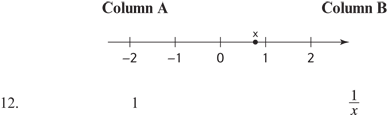
12. B On the number line, x is between 0 and 1. Therefore, x is a positive fraction less than 1. Plugging in a simple value for x (use 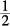 , an easy-to-work-with fraction less than 1), we find Column B equals
, an easy-to-work-with fraction less than 1), we find Column B equals 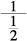 , which equals 2.
, which equals 2.
Every other fraction less than 1 will also make Column B greater than 1. Therefore, Column B is greater than Column A.
13. B Note that the only difference in the two columns is the signs of the last values, 610. Since Column B is positive (+610) and Column A is negative (–610), Column B is greater than Column A. Actually calculating the numerical values is a waste of time and not necessary.
14. C Canceling in Column A gives
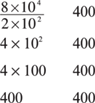
The columns are equal.
15. C In Column A, the probability of randomly selecting a blue peg is 3 out of a total of 6, or 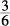 or
or 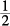 . In Column B, the probability of randomly selecting a color other than blue is 2 + 1 out of 6, or, again,
. In Column B, the probability of randomly selecting a color other than blue is 2 + 1 out of 6, or, again, 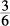 , or
, or 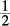 . The columns are equal.
. The columns are equal.
Algebra
1. A First, subtracting 2 from both sides gives 3x in Column A and 2x + 1 in Column B. Since x > 2, start by plugging in values greater than 2 for x. Trying 2.1, then 3, then, say, 10, you'll find that Column A will always be larger.
2. B Solve each equation:
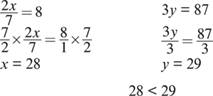
3. D Trying some values in the equation gives different outcomes. For example, when s = 4 and r = 5,
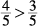
s < r
When s = –4 and r = –5,
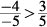
s > r
No determination is possible.
4. B Substituting a value for x and considering the given condition (x is a negative fraction) makes it evident that Column B will always be positive and Column A will always be negative. Let 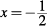 :
:

5. C This is really an example of the distributive property and can be solved by inspection. Or using an alternate method, let r = 3 and s = 2. Then
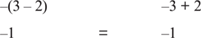
6. D Let a = 0 and b = 0. Then both columns are obviously equal. If a = 1 and b = 0, then Column A is greater than Column B. Therefore, the answer cannot be determined.
7. D Because x must be less than 4, Column A (x + 4) can equal any value less than 8. Because y must be more than 4, Column B (y – 4) can be any value more than 0. Therefore, between the range of 0 and 8, Column A and Column B could be equal or one column could be greater than the other. Therefore, no relationship can be determined.
8. C By changing the value of 1 in Column A to equal 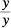 , Column A can also equal
, Column A can also equal 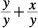 , which, combined into one fraction, equals
, which, combined into one fraction, equals 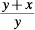 . Therefore, the two columns are equal. Likewise, Column B could've been broken into two fractions:
. Therefore, the two columns are equal. Likewise, Column B could've been broken into two fractions: 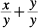 , which is the same as
, which is the same as 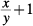 and, thus, equal to Column A.
and, thus, equal to Column A.
9. B Find the averages and simplify:
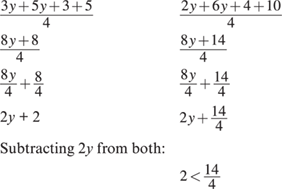
10. A Simplifying each column leaves
xy + 3x + 2y + 6 xy + 2x + 3y + 6
Subtracting xy, 2x, 2y, and 6 from both sides leaves
x > y
from the condition given, 0 < y < x.
11. A Solving each problem, first for x: 15 is 30% of x.
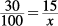
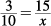
Cross-multiply:
3x = 150
x = 50
Solving for y: 12 is 25% of y.
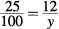
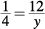
Cross-multiply:
y = 48
50 > 48
12. D Trying the value m = 1 gives

Now, letting m = 2 gives

No solution can be determined because different values give different answers.
13. C Cross-multiply the given equation:
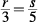
leaves 5r = 3s.
14. B Substituting x = 1 and y = 1 gives
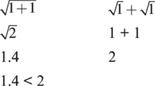
Trying other values gives the same result.
15. D By inspection, the two given equations are the same: x + 3y = 7 is the same as 4x + 12y = 28 if the second equation is simplified by dividing by 4. Because the two equations are equivalent, no definite values for x and y can be determined.
Geometry
1. A That y = 80° is evident by the diagram and the rules of a transversal through parallel lines. You know that x = 100° because x + 80 must equal a straight line of 180°, or 180 – 80 = 100. Therefore, 100 > 80.
2. B Because the circumference of a circle equals 2πr, the circumference of the semicircle in Column A equals 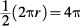 . Because π equals about 3, Column A equals approximately 12 inches. In Column B, if each side of a pentagon equals 4 inches, its perimeter equals 5 times 4 = 20 inches. Therefore, Column B is greater.
. Because π equals about 3, Column A equals approximately 12 inches. In Column B, if each side of a pentagon equals 4 inches, its perimeter equals 5 times 4 = 20 inches. Therefore, Column B is greater.
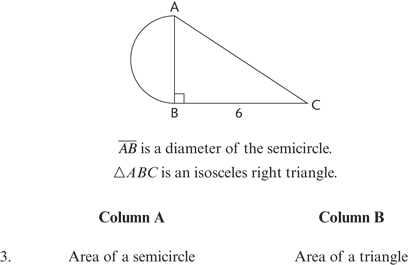
3. B AB = 6 because  ABC is isosceles. The radius of the semicircle is
ABC is isosceles. The radius of the semicircle is
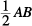 , or 3. Using the area formula for the circle:
, or 3. Using the area formula for the circle:
A = πr2
A = π(3)2
A = π(9)
A ≈ 28
Taking 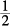 of this leaves the area of the semicircle as approximately 14.
of this leaves the area of the semicircle as approximately 14.
Now, using the area formula for the triangle:
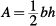
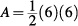
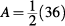
A = 18
14 < 18
4. A Using the circumference formula for a circle of diameter 6:
C = πd
C = π(6)
C ≈ 18
Taking  of this leaves 9 as the length of
of this leaves 9 as the length of  . Now, using the Pythagorean theorem to find AC:
. Now, using the Pythagorean theorem to find AC:
(AB)2 + (BC)2 = (AC)2
(6)2 + (6)2 = (AC)2
36 + 36 = (AC)2
72 = (AC)2
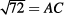
Since 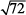 is approximately 8.5,
is approximately 8.5,  .
.
5. C Since  ABC is an isosceles right triangle, ∠A = ∠C and ∠B = 90°. This leaves 90° to be divided evenly between ∠A and ∠C. Therefore, ∠A is 45°.
ABC is an isosceles right triangle, ∠A = ∠C and ∠B = 90°. This leaves 90° to be divided evenly between ∠A and ∠C. Therefore, ∠A is 45°.
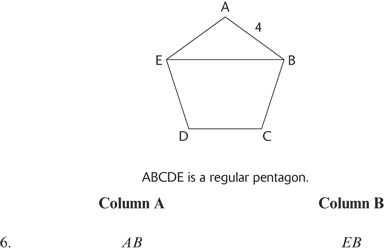
6. B Any diagonal of a regular pentagon is greater than any of the sides. Using an alternate method, use the formula for finding the interior degrees of a polygon—180(N – 2) using 5 for N (number of sides of a pentagon):
180(N – 2)
180(5 – 2)
180(3)
540
There are 540° in the interior angles of the pentagon. Dividing this by 5 for the number of equal angles, leaves 108° in each angle. ∠A is 108° in  ABE and, therefore, is the greatest angle in the triangle. The longest side of a triangle is across from the largest angle, so AB < EB.
ABE and, therefore, is the greatest angle in the triangle. The longest side of a triangle is across from the largest angle, so AB < EB.
7. A As you know from the previous problem, the sum of the interior angles of pentagon ABCDE is 540° and 540° > 360°. Using an alternate method, the sum of the interior degrees of a pentagon can be derived by dividing the pentagon into triangles as shown:
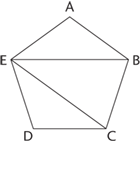
Because there are three triangles and 180° in a triangle, there are 3 × 180° = 540° in the pentagon.
8. C Because the pentagon is equilateral, AB = AE, and, therefore, ∠AEB = ∠ABE, because angles opposite equal sides in a triangle are equal.
9. A As shown in the previous problems, each angle of the pentagon is 108°. Therefore, 108° + 108° = 216°, and 216° > 180°.
10. A The sum of any two sides of a triangle is greater than the third side.
11. B If p = 90°, then c2 = a2 + b2, but since p < 90°, the opposite side, C, gets smaller. Therefore, c2 < a2 + b2.
12. A The sum of any two sides of a triangle is greater than the third side. Therefore, the difference of any two sides of a triangle is less than the third side. Solving algebraically, a + b > c. Subtracting b from both sides leaves a > c – b.
13. C Since all sides of a square are equal and each corner of a square is 90°,  ADC and
ADC and  ABC would each become isosceles right triangles. The acute angles in an isosceles right triangle each have measures of 45°. Therefore, ∠DAC = ∠BCA.
ABC would each become isosceles right triangles. The acute angles in an isosceles right triangle each have measures of 45°. Therefore, ∠DAC = ∠BCA.
14. C Using the Pythagorean theorem to find the length of diameter AC gives
(AB)2 + (BC)2 = (AC)2
(1)2 + (1)2 = (AC)2
1 + 1 = (AC)2
2 = (AC)2
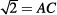
Since the radius is 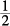 of the diameter,
of the diameter, 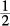 of
of 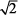 is
is 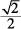 and
and  .
.
15. A Using the proper formulas:
A = s × s (area of a square)
A = πr2 (area of a circle)
and substituting s = 1 and 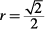 from the previous problem,
from the previous problem,