Physics is related to the early weapons of war just as it is to the more sophisticated later weapons. So far we have talked mostly about chariots, men on horses, bows and arrows, spears, and such things as the ballista, the onager, catapults, and trebuchets. Physics is involved in all of these things, but we haven't shown how it is involved. In this chapter we will do this, but first we will discuss the basic concepts of physics, beginning with the most basic ones, such as speed and acceleration, and proceeding through to more complicated ones, such as energy and momentum.

VELOCITY AND ACCELERATION

Everyone knows that if you shoot an arrow into the air it rises to a certain point before falling back to earth. It's also known that its speed as it leaves the bow depends on how hard the string pushes on it, and it's easy to see that its speed throughout its flight is not the same. After all, if you shoot it straight upward, it stops at some point before it starts to fall back to earth.

We have a slight problem in relation to motion on earth, however. Every object that moves has to pass through air, and this air has an effect on its speed as well as the path it takes. Dealing with the effect of air, however, is rather complicated, so for now we will ignore it.

The first thing we can say about an object in motion is that it has a certain speed relative to the surface of the earth. Speed is a useful concept, but even better (as far as physics is concerned) is velocity. Speed is defined as the distance something travels in a unit of time, say, a second, or even in hour. An arrow, for example, can have a speed of fifty feet per second. The problem with this is that it doesn't tell us anything about the direction that the arrow is traveling. If we specify both speed and direction, we have velocity. The velocity of the above arrow, for example, might be fifty feet per second in a northern direction.

If we look at this arrow a little closer, however, it's easy to see that it doesn't have a constant velocity. Its velocity is continually changing, and the biggest change will occur when it is shot directly upward. After all, it stops at its highest point. We refer to this change in velocity as acceleration. The arrow might leave the bow with a velocity of fifty feet per second, but a few seconds later it will be going only ten feet per second. Acceleration is clearly different than velocity, and it therefore needs a different unit. The unit in this case is feet per second squared (in the metric system it is meters per second squared). Velocity and acceleration are related by a simple formula: velocity (v) equals acceleration (a) × time (t), or more simply v = at.1

FORCE AND INERTIA

Closely related to velocity and acceleration is another important physics concept called force. For an arrow to gain speed—in other words, to accelerate—it must undergo a force, and as I mentioned earlier, it is the string of the bow that applies the force to the arrow. A force is simply defined as a push or a pull. And force is like velocity in that it has both magnitude and direction (we refer to such a quantity as a vector).²

We can relate force to acceleration, but before we do, let's introduce another important concept from physics. Everyone knows about weight, and how it seems to creep up on you when you eat too many chocolates. What we're interested in is closely related to weight, but it's not exactly the same. We refer to it as mass, and we abbreviate it as m. The mass of an object is its weight divided by the acceleration of gravity, which is usually abbreviated as g. I'll explain a little later why we need mass rather than weight.

The relationship between force and acceleration was given by the English physicist Isaac Newton. He included it in three laws of motion that he published in his Principia in 1687. He explained that an acceleration created by a force acting on a body is directly proportional to the magnitude of the force and inversely proportional to the mass of the body. We can write this an algebraic form as a = F/m. As it turns out, it is more convenient to use metric units in this formula (instead of the units you are probably more familiar with, namely feet, miles, and so on, which are units in what is called the British System). Within the metric system, however, we have two systems, referred to as cgs (centimeter, gram, second) and mks (meter, kilogram, second). In the mks system, acceleration is measured in meters per second squared, mass is measured in kilograms, and the unit of force is the Newton. In the cgs system, acceleration is measured in centimeters per second squared, mass is measured in grams, and the unit of force is the dyne, which is the force required to cause a mass of one gram to accelerate at a rate of one centimeter per second squared.

The above formula is usually written as F = ma. So the force on an object is the product of mass and acceleration. For example, if you want to create an acceleration of 25 km/sec² in an arrow with a mass of .01 kg you would need a force of .01 × 25 = .25 Newtons.

Closely related to the concept of a force is what is called inertia. We encounter inertia every day; when you push on an object or lift it, you have to exert a force to get it going. If an object is not moving—in other words, it's just sitting there—it tends to resist motion, and it takes a force to get it going. Indeed, the heavier it is, the greater the force that is needed. This “resistance” to a change in motion is called inertia, and Newton described it in his first law of motion: a body will continue in a state of rest or uniform motion in a straight line unless acted upon by a force. Note that this applies not only to something at rest, but also an object in uniform motion.

This means we need a force to overcome inertia, and this force produces acceleration according to the above formula. Furthermore, a force is always associated with two bodies. If one body is being pushed, the other body has to do the pushing. This also applies to an object sitting on the floor; because of its weight it pushes down on the floor. But according to Newton, the floor pushes back with an equal force in the opposite direction. Newton postulated this in his third law of motion: whenever a body exerts a force on a second body, the second body exerts a force on the first body. These forces are equal in magnitude and opposite in direction. They are frequently called the “action” and “reaction” forces. A good example of these forces can be seen when you hold a garden hose with water pouring out of it. You feel a backward force on your hands; this is a reaction force, and it's why rockets work: explosive gases shoot out the back of the rocket, giving the rocket its forward thrust.

MOMENTUM AND IMPULSE

Another important concept in physics is momentum; it is the product of mass and velocity (m × v). It is particularly important when one object collides with another. As you no doubt know, when a massive object collides with a smaller, lighter one, it's the smaller one that suffers the most. To understand this more fully we have to introduce the concept of impulse. Assume a soldier hits the shield of another soldier with his sword; he's obviously applying a force to it, but this force is only exerted over a short period of time. The product of this force, and the time it acts, is defined as impulse. Furthermore, it's obvious that this impulse is going to cause the shield to move with a certain velocity, and this velocity will depend on the mass of the shield. So impulse is somehow also related to momentum. Indeed, the impulse creates momentum; or, to be more precise, since the momentum of the shield was zero before the impulse, the impulse creates a change in momentum. So impulse is equal to change in momentum.3

Now let's go back to our discussion of the collision of two bodies. Of particular importance in relation to such a collision is what is called the principle of conservation of momentum. It states that the total momentum of any isolated system remains constant. This means that the total momentum before the collision will be equal to the total momentum after it, assuming there are no outside influences. Let's assume that the collision is a head-on collision, and that both objects have the same (but opposite) momentum. It's pretty obvious that they will stop dead. It almost seems as if their momentum has disappeared—but it hasn't. Before the collision they had equal but opposite momenta, and the sum of two equal and opposite numbers was zero. After the collision it's still zero. As the collision occurred, each object imparted an impulse on the other, but the impulses were equal and opposite, so the objects stopped.

It's easy to see from this that if one of the objects has a greater momentum than the other, it will generate a greater impulse on the second, and if the two objects stuck together when they collided they would continue with a certain velocity in the direction of the one that had the greatest momentum.

THE EFFECT OF GRAVITY

Everyone knows that when you shoot an arrow at some angle in an upward direction, it doesn't travel in a straight path. It travels upward for a while then heads back toward earth, eventually landing. This is because of the gravitational pull of the earth on the arrow. In reality, the two objects are attracted to one another, but because the earth is so much more massive than the arrow, it appears to us that the earth is attracting the arrow. Again, it was Newton who explained what is going on. He postulated that all objects in the universe attract one another. Indeed, he even gave a formula for the force between any two objects.

Let's begin by considering a stone held at some distance above the ground. It is attracted by the earth with a certain force, and if we let it go, it accelerates downward until it strikes the ground. With a relatively simple apparatus we can measure this acceleration, and we find it to be 32 ft/sec², or in metric units, 9.8 m/sec².

Gravity is particularly important in relation to warfare because all objects, such as arrows, cannonballs, bullets, and so on, are affected by it. Such projectiles trace out trajectories that depend on several things, such as their mass and speed, and also the air pressure. (We'll talk about trajectories in detail later in the book.)

The acceleration of gravity is not the same everywhere, however. It depends on the mass of the planet you happen to live on. So if you were to travel to Mars or Jupiter, it would be different. As a result, your weight would also be different. On Jupiter for example, you would weigh 2.34 times your weight on earth. What is constant is your mass; it doesn't depend on the gravitational field you happen to be in, and that's why it is used in most of the basic physics equations. The relationship between mass (m) and weight (W) is given by W = mg, where g is the acceleration of gravity.

ENERGY AND POWER

If you lift something in an upward direction through a certain distance you do work. To perform this work it takes energy, and, as it turns out, there are several different forms of energy. Two of the most common forms are energy associated with motion, and energy associated with position. Energy associated with motion is called kinetic energy, and since it depends on motion, it will also have to depend on velocity. Furthermore, an object with a greater mass will have more kinetic energy than one with less mass, so kinetic energy also depends on mass. It is therefore defined as kinetic energy = 1/2mv², where m is mass and v is velocity. Its units are foot-pounds in the British System and Newton-meters in mks units.

Energy of position is called potential energy. It also has the ability to do work. Consider a stone held at some position above the ground. If you drop it, it does work on that dirt it strikes; it compresses and heats it slightly. We define it as potential energy = mgh, where m is mass, g is acceleration of gravity, and h is the distance above the ground from which it was dropped.4

Like momentum, energy is also conserved. In short, the conservation of energy states that energy can neither be created nor destroyed; it can only change from one type of energy to another. This can be demonstrated quite nicely if you take a ball and throw it upward. When first thrown, the ball has a high velocity, and its energy is therefore mostly kinetic energy. As it continues to rise, however, it gradually decelerates because of the pull of gravity. Finally, it stops, and at this point it has zero velocity, and therefore it has no kinetic energy. In essence, all its kinetic energy has been converted to potential energy, so at this point it only has potential energy. As it begins to fall again, however, its speed increases, and its kinetic energy also increases. At the same time, its potential energy decreases, and by the time it is just about to hit the ground all its potential energy has been converted back to kinetic energy.

The two above types of energy are not the only two types of energy. Other forms are deformational energy, heat energy, sound energy, electrical energy, chemical energy, and nuclear energy. You might, for example, ask what happens to the kinetic energy of the ball when it hits the ground. It appears to be lost, but it isn't. It is converted to deformational and heat energy.

In many cases we are not interested in the work (or energy) that has been done, but rather the rate of the work, or the amount of work accomplished per unit of time. This is referred to as power. In mks units, power is measured as joules per second, and by definition a joule/sec is a watt.

ANGULAR MOMENTUM AND TORQUE

Another type of motion that is important in relation to warfare and weapons is rotational motion. The wheel, or anything that spins about an axis, has angular or rotational motion. And just as we have linear velocity and linear acceleration, we also have angular velocity and angular acceleration. Angular velocity is measured as the number of revolutions per unit of time. Another common unit is the number of radians (rad) per unit of time, where the radian is 360/2π ≈ 57.3 degrees (360 is the number of degrees in a circle and π is the circumference of a circle divided by its diameter, which is 3.1416). Angular speed can, of course vary, and when it does it becomes angular acceleration. Its units are revs/sec².5

In the same way we have a concept analogous to force. It's the force that causes the rotational motion, and it is called torque. It has to be applied at some distance from the rotational axis to cause rotation, so there is also a distance involved. Torque is defined as force × distance (f × r). Note that you apply torque every time you use a wrench or open a door.

Earlier, in the case of translational or linear motion, we also had momentum, and in the same way we have angular momentum in this case. To determine the formula for it we must replace mass (m) and velocity (v) by appropriate angular quantities. Velocity is no problem; we merely replace it with angular velocity (ω), but m is a little more complicated because we are dealing with a large number of small masses, each at a different distance from the axis. If we add up all the little contributions from these small masses we can determine what is called the moment of inertia; it is designated by I. Angular momentum is then Iω.

MACHINES

Many of the early weapons were what we call machines in physics. A machine is a device that makes work easier. A simple example of a machine is a long board used to raise a box that is too heavy for us to lift. If you place one end of the board under the box, and place a block (called a fulcrum) a few feet away, then apply a downward force to the other end of the board, you find you can easily raise the box. This makes sense because work is force × distance; when we apply the force the box is raised a smaller distance than the top of the board moves. We are, in effect, using the extra distance to get a greater force. The work done is equal, but it is easier for us because we only have to apply a fraction of the force we would have to if we were lifting the box directly. This is basic to all machines.6

Many types of machines exist, and the principles associated with each of them were used in various early weapons. Some of the more common machines are:

Pulleys: They allow heavy loads to be lifted with less force; you merely have to move the rope a greater distance than the load moves.

Wheel and axle: A longer twist at the outer edge of the wheel exerts a more powerful but shorter motion near the axis.

Screw: Applying a larger but easier rotary force creates a smaller forward motion.

PHYSICS OF THE BOW AND ARROW

The bow and arrow was used extensively in early warfare. Archers were trained from an early age. In some cases they advanced toward the enemy on foot, carrying a shield; in others cases they rode in chariots. As we saw in the last chapter, chariots usually had a driver and an archer, and when the chariot got close enough to the enemy, the archer would begin firing arrows as fast as he could.

A bow, in essence, is a simple machine that changes one type of energy into another, making it easier for the archer to give the arrow a high velocity. What is needed for a high velocity is a rapid and forceful arrow movement, and of course muscles can do both of these, but not at the same time. To understand the physics of the bow and arrow let's begin with the archer loading an arrow and pulling the string back slowly. He is using his arm muscles to do this. He pulls the string back to its maximum extension, and in the process the bow bends. The energy from the archer's muscle contraction is stored in the bending of the bow. This is potential energy. He then lets go of the bowstring, at which point the string moves rapidly to the normal rest position. In the process it transfers energy from the bow to the arrow. In essence, potential energy is transferred to kinetic energy, as in the case of a falling ball. The transfer is obviously very rapid, and this gives the arrow a high speed. Note that the archer has produced a certain amount of energy, and by the conservation of energy, this energy must remain constant. But the bow can move with both a high force and a high velocity in a way that his arm cannot. The bow is a machine that stores energy. Muscle power is used to load the machine at low speed, then the machine releases the energy at high speed. Indeed, if you know all the variables, such as the mass of the arrow, the distance the bow is pulled back, and what force it exerts, you can equate potential energy to kinetic energy and determine how fast the arrow will leave the bow. Furthermore, if you know the angle at which is it is aimed (and ignore air pressure) you can determine how far it will go.⁷

Over the years bow and arrows were gradually improved. Several factors are important in relation to how powerful a bow will be. Three of the most important are its length, its shape, and its composition. In general, the longer the bow, the more powerful it will be, but other factors play a large role. We will see later that the English developed a very effective longbow and used it with considerable success against the French.

The overall shape of the bow is also important. Early bows had a single curve and were made of wood. Eventually, however, archers determined that if the ends of the bow were curved away from the user, the arrow would go farther. This was because the curving shortened the distance between the bow and the string at rest, and as a result, the string traveled farther before coming to a stop as it released the arrow. This extra push gave the arrow a little more momentum and speed. This type of bow is called a recurved bow.

The bow's composition was, of course, also critical. The type of wood, or other material, it was made of had a large effect on its power. Also, a bow's density, elasticity, and tensile strength (amount of stress it can take before it breaks) determines how much energy it can store and how well it returns to its original shape after the shot.

Early on it was discovered that bows made from more than one material were more effective than simple wood bows. They are referred to as composite bows. Composite bows were usually made of wood, a section from the horn of an animal, and sinew. A thin section of horn was glued to the belly of the bow on the side facing the archer. Horns from antelope, water buffalo, and sometimes sheep or goats were used. This allowed more energy to be stored in the bow. The glue was made from fish oil. Strips of sinew were also glued along the back of the bow, again to increase the energy storage. The tips (recurved sections) were also stiffened using sections of bone.8

Arrows were continually improved over the years. One of the most critical concerns was the weight of the arrow. If an arrow was too light it would be affected by the movement of air and would not stay on course well. If it was too heavy, on the other hand, it would create a lot of drag and fall too fast. The ideal weight was somewhere in between. It was also discovered early on that feathers along the sides increased an arrow's stability, and that the length and height of the feathers had an effect on how far the arrow went, and on its stability in flight.

A variation on the ordinary bow and arrow is a crossbow, which is known to have been used by the early Greeks. It fired a steel bolt, and initially the drawstring had to be drawn back by the archer and locked into position, then released using a trigger. This made loading slow, and considerable strength was needed to pull the string back. Eventually, however, a mechanical winch system was developed for loading, and with it, a much greater tension could be put on the string. As a result, the steel bolt left the bow with a much greater velocity, and it therefore had a greater range. The crossbow could, in fact, project a bolt up to five hundred yards. But the problems didn't go away. The steel bolts were not very aerodynamic, and as a result they were also not very accurate. In addition, they were much slower and much more difficult to load than an ordinary bow. At maximum, a crossbow could be fired about twice every minute whereas a good archer could fire twelve to fifteen arrows a minute. Initially, however, crossbows had a serious advantage over the ordinary bow: the steel bolts they fired could penetrate the steel armor shielding of the enemy. Furthermore, the bolts could easily kill a horse. Eventually, however, the English invented the longbow, which also packed enough power to penetrate armor.

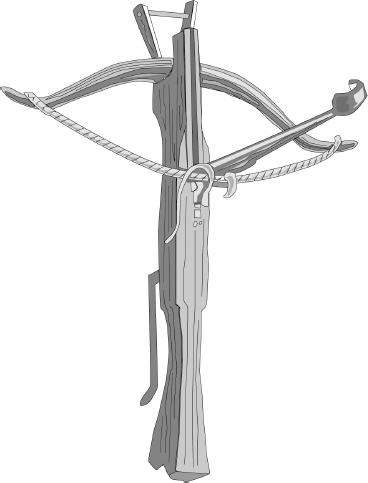
A crossbow.

Although it was not used in early wars, a significant advance was eventually made in bows. A bow is, of course, hard to draw back, but the greater the energy you expend in drawing it back, the greater the energy it transfers to the arrow. And again machines came to the rescue. Pulleys were eventually used to help archers do more work on the bow (and produce more potential energy) with less physical effort. The compound bow allows an archer to hold and aim a drawn bow without a lot of stress or fatigue.

PHYSICS OF OTHER EARLY WEAPONS

Most of the early weapons were devices of one sort or another that projected either arrows or stones. Most were, in fact, catapults of some sort. As we've already discussed, three of the best known were the ballista, the trebuchet and the onager. The ballista was a torsion spring, which stored energy in several loops of twisted skeins. It could project heavy iron-tipped darts or stone projectiles of various sizes. The darts were placed in a shallow wooden trough or groove. The ballista was armed by hooking a bowstring behind the dart and winding it back using a windlass. It pulled a sliding trough and the dart within it back, and at the same time it twisted the skein (the bow string was attached to two arms, each with its own twisted skein). Ratchets and cogs prevented it from shooting while it was being loaded. Once loaded it could be fired using a trigger. Again, we have potential energy of torsion in the twisted skeins, and when it was released, it was converted to the kinetic energy of the dart.

The earliest ballista were developed about 400 BCE. The best ones had a range of about five hundred yards. They used only relatively light projectiles, so they didn't hit with a lot of force, but they were relatively accurate.

The trebuchet was much more powerful, and it worked on a completely different principle. It is, in fact, sometimes called the “counterweight trebuchet” because it used a counterweight to produce the energy for throwing the projectile. It is said to have first been used by the French in the twelfth century, and is based on the principle of the fulcrum described earlier. Its major part is a long arm anchored above the ground close to one end. At the end of the long arm is a sling that contains a pouch; this is where the projectile (usually a large stone) was placed. The energy came from a heavy weight placed at the end of the shorter arm. It was raised up and held in place until ready. Again, we have potential energy being converted into the kinetic energy of a projectile. When the trigger was released, the sling and longer arm would swing upward toward a vertical position. At this point the sling would release and the pouch would open. The projectile would be thrown forward with considerable velocity. The device was, in effect, powered by gravity.

The advantage of the trebuchet was that it could project stones of up to three hundred pounds, which could do considerable damage to the upper parts of most castle walls. It had a range of about three hundred yards. It's important to note that the sling played an important role; it could double the power of the trebuchet, allowing it to throw a projectile twice as far as it would have been able to without the sling.

The third of these catapults, called the onager, was similar to the ballista in that it also used torsional pressure generated by twisted-sinew ropes. It consisted of a large frame on the ground with a vertical frame attached to it. A spoke, or arm, was attached to an axle that ran through the vertical frame. A bowl-shaped bucket was placed at the end of this arm, with the projectile placed in this bucket. The machine was loaded by pushing the arm back against the tension created by the twisted skeins. When the trigger was released, the arm would swing upward in an arc, releasing a projectile at the top of the swing. As in the case of the other devices, large stones were usually used as projectiles. Onagers usually had a range of about twelve hundred feet.