
In an earlier chapter we were introduced to the problems related to the accuracy of rifles and cannons. For many years, in fact, gunners had no idea what the trajectory of a bullet looked like. Tartaglia made some important advances, and Galileo clarified many of the problems related to gravity, but it was Newton who finally showed why and how gravity was involved. In this chapter we will look much more closely at the problem, and although we have discussed only muskets, rifles, and cannons up to the time of the Civil War, we will also deal with more modern rifles and cannons in this chapter.
The study of ballistics is concerned with the motion of projectiles, but it is also concerned with what happens to the projectile, or bullet, inside the gun, and also what happens when it hits a target. In all, there are four basic areas of study within this topic:
- Interior ballistics
- Transitional ballistics
- Exterior ballistics
- Terminal ballistics
Interior ballistics is concerned with what happens between the firing of the cartridge and the exit of the projectile from the muzzle. Transitional ballistics, which is also known as intermediate ballistics, is a study of the projectile from the time it leaves the muzzle until the pressure behind the projectile is equalized (in other words, when the air pressure behind the projectile is equal to the surrounding air pressure). Exterior ballistics deals with the projectile while it is in flight under the influence of gravity. Terminal ballistics is the study of what happens to the projectile after it hits the target. I will talk mostly about rifles, but much of what I say also applies to cannons.
INTERNAL BALLISTICS
Internal ballistics depends on what happens inside the breach and barrel of the gun, so it is the best place to begin our discussion. Of particular importance, the trajectory depends, to a large degree, on what is referred to as the muzzle velocity, which is the speed of the bullet as it leaves the end of the barrel. So let's look at how muzzle velocity develops. Two separate events are critical here: ignition of the gunpowder, and expansion of the gases that develop as a result of the initial explosion. Ignition occurs when the firing pin hits the percussion cap (or primer) and causes it to explode. This, in turn, ignites the gunpowder in the cartridge. As the gunpowder explodes, the gases produced by the explosion are trapped behind the projectile. They are at high temperature and therefore create pressure that accelerates the projectile down the barrel. It is particularly important that the burn time is less than the time it takes the projectile to reach the end of the barrel. If not, powder will come out of the barrel still burning, and this would create a dangerous situation.1
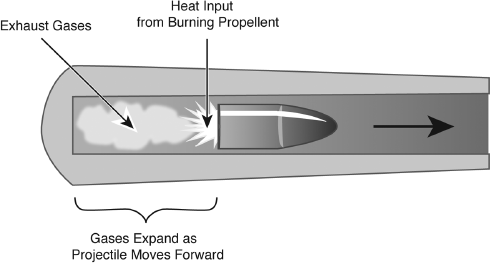
Expanding gases behind a bullet in a barrel.
As the gas expands, it cools according to the basic gas law discovered by Jacque Charles in the late 1800s, which is now referred to as Charles's law (it is sometimes referred to as Gay-Lussac's law, since it was discovered by Joseph Louis Gay-Lussac about the same time).2 This law tells us that pressure times volume is proportional to temperature, and therefore a sudden increase in temperature will create an increase in volume that will impart a higher pressure on the projectile. Inside the barrel the pressure does, indeed, increase initially, but as the projectile moves forward, the pressure decreases. A plot of pressure versus distance along the barrel is given below. We see that the pressure reaches a peak rather quickly before dropping rapidly. The maximum pressure is important because it occurs mainly in the breach area of the gun, and this area has to be able to withstand the pressure. This is why the steel of guns and cannons is thickest in this area. The rearward push on the gun's bolt, or breach, which results from the explosion, is referred to as the bolt thrust. It depends on both the chamber pressure and the diameter of the cartridge case. And it's important that the design of the gun is sufficient to withstand the bolt thrust. The pressure in this area (the chamber) is usually measured in pounds per square inch (psi), or in the metric system it is measured in kilograms per square centimeter (kg/cm2). Typical pressures in this area depend on the type of gun, but for rifles it is approximately fifty thousand pounds per square inch.
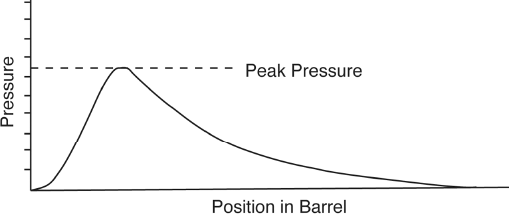
A plot of pressure versus distance along the barrel.
It's fairly obvious that the longer the projectile is accelerated by the explosive force, the faster it goes. The law controlling this is Newton's second law, which states that force is equal to mass times acceleration (F = ma). And this acceleration continues as long as the projectile is in the barrel (and slightly beyond, as we will see later). So the longer the barrel, the greater the velocity of the projectile when it exits; this is called the muzzle velocity. And although longer barrels provide greater velocity, there is a limit. Very long barrels are hard to handle, and the weight of the gun also increases with barrel length.
The length of the barrel is important in another way. As the hot gas explodes down the barrel, it decreases in pressure, and ideally it should not be much higher than atmospheric pressure when it reaches the end of the gun. In practice, however, it is usually much higher. As a result, it creates a shockwave as it hits the air. The problems related to this will be discussed in the section on transitional ballistics.
In addition to barrel length, the muzzle velocity also depends on the mass, or weight, of the projectile for a given amount of explosive; a lighter projectile will emerge with a greater muzzle velocity. The type of powder in the barrel is also an important factor; different types of powder have different propellant energies. How much powder should be used is also a factor, but for a given caliber, there is a limit on the amount of propellant.
Another important question is: What is the maximum velocity that a projectile can be pushed to without extreme danger to the gunner? In rifles this is about four thousand feet per second. Large-caliber guns and cannons can safely be pushed to about six thousand feet per second.
RECOIL
It's important to note, however, that higher muzzle velocities have another problem. As we saw earlier, Newton's third law tells us that for every action there is an equal and opposite reaction. The action in this case is the force pushing the projectile and the hot gases out of the barrel, creating the muzzle velocity. The reaction is therefore opposite to this, and the gunner feels it as the gun's recoil. The direction of the recoil force is directly opposite to the force that pushes on the projectile. Anyone who has ever shot a gun has experienced recoil, and at times it can be quite strong. Directly related to the third law is the conservation of momentum. We can write it as mv = MV, where m and v are the mass and velocity of the projectile, and M is the mass of the gun (or the gun and gunner) and V is the recoil velocity. The mass of the gun is much greater than the mass of the projectile, but the muzzle velocity of the gun (v) is extremely large, so without constraint, the gun would achieve a relatively high velocity. But it is constrained by your shoulder, and this creates a relatively large force on it, which slows its velocity very rapidly. Gunners are, in fact, told to hold the gun snugly against their shoulders so that M includes not only the mass of the gun, but also the mass of the gunner.3
Also, in movies and TV, you've likely noticed that the actors always hold their revolvers with two hands in an effort to steady them. One of the reasons for this is that recoil tends to cause the revolver to turn upward. This is caused by an upward torque that occurs because the recoil force is pointed along the barrel of the revolver, but the revolver is held by a lever, namely your arm and shoulder. Since this force is at an angle to the level arm, it creates it torque, causing the barrel to move back and turn up at the same time.
One of the major ways to reduce the effects of recoil is to have a recoil pad at the end of the gunstock.
TRANSITIONAL BALLISTICS AND THE SONIC BOOM
Transitional ballistics is sometimes referred to as intermediate ballistics because it is concerned with the projectile behavior in the time between internal and external ballistics; in other words, the brief time from when the projectile leaves the barrel until the pressure behind it reaches the pressure of the surrounding air. When the bullet reaches the end of the barrel, the gases behind it are frequently at a pressure several hundred times that of atmospheric pressure. When the bullet flies free of the barrel, however, the gases behind it are free to expand and move outward in all directions. This sudden expansion causes a loud explosive sound, namely the boom that you hear when a gun is fired. It is also sometimes accompanied by a flash as the gases combine with the oxygen of air.4
This is the first boom you hear when a gun is fired, but in many cases there is also a second boom, referred to as a sonic boom (it will be discussed a little later in the section). Earlier I mentioned that the bullet accelerates as it moves up the barrel because it is being pushed by the expanding gases, but once it leaves the barrel it has a uniform horizontal velocity. This is not exactly true. There is still a force on the bullet for a short time after it leaves the barrel due to the expanding gases behind it. This is one reason why the “muzzle velocity” of a rifle is not measured at the end of the barrel, but several feet in front of it.
In the design of a gun it is important to make sure that the gases that expand behind the bullet as it leaves the gun do not disturb the bullet from its path. If it is somehow pushed off to one side, the accuracy of the rifle would be compromised. So the gun has to be designed so that this doesn't occur; in short, the designers have to make sure the gases expand symmetrically around the base of the bullet.
In the case of military weapons—particularly sniper rifles—it is important to decrease the sound and flash from the rifle as much as possible so that the position of the sniper is not given away. This is done by flash and sound suppressors; in both cases devices are used to change the flow of the escaping gases. In the case of flash suppressors, turbulence in the escaping gas is introduced in an attempt to reduce the combustion efficiency of the flash. In the case of sound suppressors the gas is allowed to cool so the velocity at which it exits the barrel is reduced; this prevents a shockwave from forming. Unfortunately, suppressors are bulky and heavy, and they are not used extensively.
But even if they reduce the shockwave from the exiting gases, there is still a sonic shockwave that can easily be heard. Let's look at this wave. It's well known that any object traveling through air at a velocity greater than that of sound will cause a sonic boom. This applies to most bullets, and, as it turns out, no type of silencer can dampen a sonic boom, since the shockwave that causes the boom travels along with the bullet.
For a supersonic shockwave, the bullet has to exceed the speed of sound, which is about 1,100 feet per second (or approximately 750 miles per hour) depending on the air pressure and a number of other factors. About one-half of all pistol ammunition is supersonic, as is virtually all rifle ammunition, and most shells shot from cannons are also supersonic. Tank guns, as I mentioned earlier, have velocities up to six thousand feet per second, which is many times the velocity of sound.
To understand the sonic boom better, let's look at how it is created. It's well known that when an object creates a sound, a wave travels outward from the object at the speed of sound. If you look closely at this wave you see that it consists of a series of compressions and rarefactions. The compressions occur because the molecules of air are pushed together in certain regions, and the rarefactions are caused because the waves spread out in other regions. This means that a wave that is uniform in all directions passes outward from the source. But when you move the object that is creating the wave, the wave pattern around it changes. The compressions get closer together in the direction that the object is traveling and farther apart in the opposite direction. Furthermore, as the object moves faster, the waves in the forward direction start merging into one another, and at the speed of sound they merge completely together.
At this point the pressure on the nose of the bullet is much greater than it is on the rear of the bullet. But sound in air can only move at approximately 1,100 feet per second, and a bullet can move at any speed; in particular, it can move at speeds greater than the speed of sound. Because of this, when the bullet breaks, or passes through the sound barrier, it creates compressions faster than the compressions themselves can move away, so they just pile up on one another. As these compressions are brought together, they do not form a smooth progression from compression to rarefaction, as they do in ordinary sound waves. Instead, there is a sharp dividing line between a volume of strong compressions and the normal atmosphere around the wave. As a result, the strong compressions stream backward in a cone-shaped band. When this cone passes an observer on the ground, he or she experiences a sudden difference in pressure as it moves by, which he or she interprets as a sonic boom. In many ways it is quite similar to the crack a bullwhip makes.
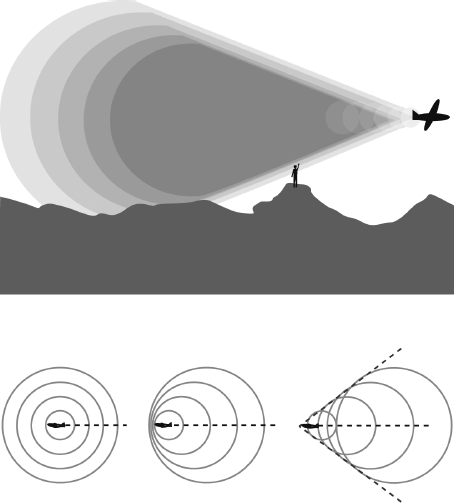
Cone that forms during a sonic boom.
EXTERNAL BALLISTICS
External ballistics deals with the behavior of the projectile in flight from the time it is just beyond the end of the barrel until it hits the target. Galileo realized that two separate motions were involved: a horizontal motion parallel to the ground, and a vertical motion. And although there were two motions going on at the same time, they could be dealt with separately. The horizontal motion was the horizontal component of the muzzle velocity, and it had a constant velocity. The vertical motion was free fall due to gravity, and it was therefore a constant acceleration of 32 ft/sec2, which is the acceleration of gravity. Galileo also showed that the overall trajectory when you combined the two motions was a parabola. (As we saw earlier, the easiest way to visualize a parabola is to take a cone and slice it somewhere along the side so that the slice passes through the base.) As it turns out, this is only approximate because of air pressure. Air pressure slows the bullet and causes the trajectory to deviate from a parabola.5
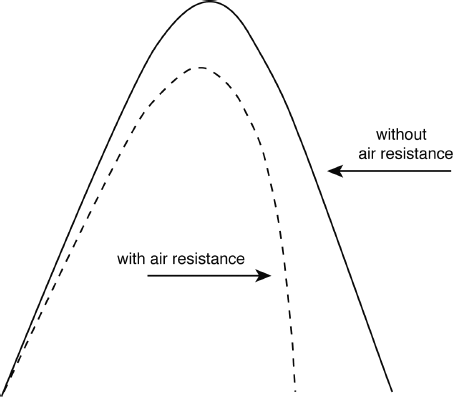
Path of a bullet with and without air resistance.
One of the things that's easy to show is that a bullet drops in the same way that something drops if you hold it above the ground and let it go. A demonstration of this is frequently used in physics classes; it has a simple projector (a gun) that throws an object straight out from it, parallel to the ground, and releases another object at the same time that falls directly downward. The first object traces out a much longer path, but the two objects hit the ground at the same time.
Let's look at the air pressure around the bullet in more detail. It creates a force called drag, which acts in a direction directly opposite to the direction the bullet is traveling. And interestingly, it is a much greater force than gravity (fifty to one hundred times greater), but gravity is still the main force that determines the bullet's trajectory. In practice, the shape of the bullet has some effect on its path, but in a first approximation we can assume gravity is acting on the bullet at its center of gravity. Basically this is just the “balance point” of the bullet.
The drag caused by air resistance actually depends on several things, such as the bullet's speed, its shape, the density of the air that it is passing through, and the air temperature. In practice, calculating drag is usually a difficult problem. Furthermore, there's a serious problem at the speed of sound, or, more specifically, when the bullet passes through the speed of sound. For this reason it is best to deal with four separate regions:
- Below the speed of sound, up to about 1,000 ft/sec.
- Just below the speed of sound, from 1,000 ft/sec to 1,200 ft/sec.
- The peak drag region, which is 1,200 ft/sec to 1,400 ft/sec.
- The supersonic region, which is above 1,400 ft/sec.
If we refer to drag as D we can see how it varies in the three regions by plotting it against the velocity of the bullet.
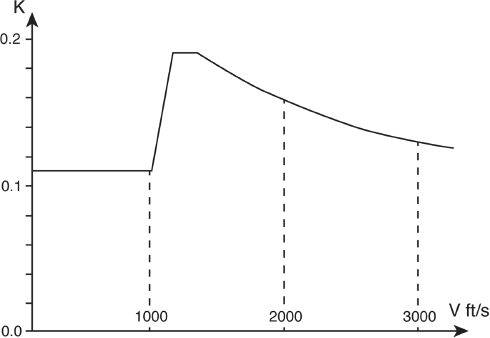
A plot of k (drag force/velocity2) versus velocity.
The ballistic coefficient (BC) is a term that denotes the rate at which the bullet slows down. In conjunction with the muzzle velocity of the bullet, it gives us a good approximation of the bullet's trajectory. The ballistic coefficient (BC) is defined in terms of what is called the sectional density (SD) and a form factor (FF). The sectional density is the mass of the bullet divided by its caliber squared. The form factor is a measure of the aerodynamic efficiency of the bullet, which depends on it shape, so it is more difficult to determine. In terms of SD and FF, the ballistic coefficient is BC = SD/FF. So if we know the ballistic coefficient, the muzzle velocity, and the angle at which the gun was aimed, we can plot the bullet's trajectory. In practice, however, you need tables giving information about the bullet, so I won't get into it in detail. But we can state the following:
- Bullets with high BCs are the most aerodynamic and bullets with low BCs are the least aerodynamic.
- High BCs are desirable because they give a flatter trajectory for a given distance.
- Bullets with high BCs get to the target faster, so their trajectories are less likely to be altered by wind or other variables.
There are other things that also affect the flight of the bullet. Wind velocity can have a serious effect, particularly if it is at right angles to the direction of flight. In addition, the wind velocity frequently varies over the distance of the flight. Yaw, which is a consequence of the spin of the bullet, can also be a problem; it is a rotation of the nose of the bullet away from the line of flight. A similar effect, called precession, also occurs in the case of a spinning object such as a bullet. It is a rotation around the center of gravity of the bullet. It is easily seen in a gyroscope. Finally, there is something that is only important in very long-range shells. It is referred to as the Coriolis force, and it is created by the rotation of the earth. In effect, the earth rotates under the shell as it moves in flight, but from the perspective of an observer on the ground it appears as if the shell is moving away from its intended trajectory.
Another thing that is particularly important in the case of guns is their maximum range. In other words, at what angle do you aim a gun for maximum range? Galileo showed that in an ideal case, where there is no air resistance, maximum range is achieved when the gun is aimed at an angle of 45 degrees to the ground. But, of course, air pressure changes things quite dramatically. We now know that rifle bullets achieve the greatest range for an angle of 30 to 35 degrees. High-velocity, large-caliber artillery, on the other hand, achieve the greatest range at an angle of 55 degrees. The maximum range of a bullet, however, is not equal to its effective range. The effective range is the range that produces reasonable damage. In general, the greater its mass, the closer the effective range is to the bullet's maximum range. Light bullets, like .22 caliber bullets, for example, have a maximum range of nearly a mile but an effective range of only about a hundred yards.
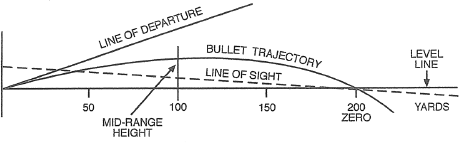
Trajectory of a bullet.
STABILITY OF THE BULLET
As we saw earlier, the main thing that stabilizes a bullet is spin, and this spin is created by the “rifled” interior of the gun's barrel. A rifled barrel has spiraled or helical grooves down its length. The bullet is forced into these grooves, which creates spin along its long axis. When the bullet emerges from the barrel, it behaves like a gyroscope. In particular, it has the stability of a gyroscope. If you have ever played with a gyroscope, you know that it takes considerable force to move it out of the direction it is spinning. This is what gives the bullet its stability and its increased range; without stability the bullet would tumble while in flight, and air pressure would act on it much more strongly.

Spiraling grooves in the barrel of a rifle.
Rifling is generally quantified by twist rate, which expresses the distance the bullet travels down the barrel while it makes one revolution, or one complete turn. The shorter the twist distance, the greater the spin rate. If you look closely at the spiraling inside the barrel, you will see that it is a series of grooves with relatively sharp edges. The spaces that are cut out along the barrel are, indeed, called grooves, and the regions that are left are called lands. This type of rifling is usually referred to as conventional riffling, but there is also another type. In this type the entire barrel is cut in the shape of a polygon (e.g., a hexagon), with the polygon shape given a twist as it goes down the barrel. It is referred to as polygonal rifling. In the case of larger shells, such as those shot from ship guns and tanks, the shell is equipped with fins that ride in grooves as they pass through the barrel.
In most cases the spiral rifling is encountered by the shell almost immediately after it leaves the chamber; in some cases, however, the spin is increased gradually. This is referred to as gain-twist. In this case there is no rifling from the chamber to the “throat” of the gun. When the bullet first leaves its cartridge, therefore, it is not spinning. However, it encounters rifling after it has traveled a short distance, and in most cases the rifling increases its twist rate gradually. This allows the projectile to spread out its increase in torque over a larger distance.
The number of grooves in the barrel can vary, as can their shape and depth. Furthermore, the twist direction can be either clockwise or counterclockwise, and the twist rate can vary depending on the bullet shape, weight, and length. In breach-loaded guns the projectile is placed in the chamber. When it is fired, “seating” occurs in the throat. The throat is usually slightly larger than the bullet, so when the bullet is fired it expands under the pressure of the gas behind it until its diameter matches that of the interior of the barrel. The enlarged bullet then travels down the throat to the rifling, where it is “ingrained”; in other words, grooves are cut into it. As a result of these grooves, the bullet begins to spin.
The twist rate given to a particular bullet is critical. First of all, it has to be sufficient to stabilize the bullet, but it should be no greater than this, and the ideal twist rate depends on the bullet's weight, length, and overall shape. Twist rates can vary considerably; older guns, for example, frequently had twist rates as low as one in seventy inches. More modern guns have much higher twist rates, such as one in twelve inches, or even one in ten inches. In general, rifles have much greater twist rates than pistols. The twist rate (T) is frequently expressed as T = L/D, where L is the length for one revolution, and D is the barrel diameter.
If the twist rate is too small, the bullet will yaw (move back and forth along the direction of flight), and if this happens, it will eventually begin to tumble and lose its accuracy. A twist rate that is too low can also cause a bullet to precess around its center of gravity. As we saw earlier, this is a motion you can easily see in a gyroscope.
On the other hand, the twist rate can also be too high. In many spinning objects there is an outside force usually called the centrifugal force (this is actually an erroneous term), and the faster the spin, the greater this force. Countering it is a cohesive force that is holding the bullet together. When the centrifugal force becomes greater than the cohesive force, the shell disintegrates and flies apart. In theory, a bullet can have a spin rate up to about three hundred thousand revolutions per minute. Most bullets, however, have spin rates much smaller than this, typically in the range twenty to thirty thousand revolutions per minute.
TERMINAL BALLISTICS
Terminal ballistics is a study of what happens to the bullet or projectile after it hits the target. It's obvious that its velocity will change rapidly. It may be stopped by the target, or it may pass through it. There are two ways in physics to deal with this case; they are referred to as the force or momentum picture, and the energy picture. In the force picture we deal with forces (or momenta), so we use Newton's third law, which says that for every action force there is an equal and opposite reaction force. In this case we are concerned with the force applied to the target, or the momentum delivered to it. In the other view, the energy picture, we are concerned with the kinetic, potential, and any other types of energy that might be involved. In most cases the energy picture is the easier of the two to use, and the major reason for this is that conservation of energy states that energy cannot be created nor destroyed; it can only be changed from one type into another. So for a given problem all you have to do is look at each type of energy involved to make sure that everything adds up. In the case of a bullet fired from a gun the chemical energy of the bullet is transformed immediately to gas pressure and heat energy in the barrel. This energy is then transferred to the kinetic energy of the bullet's motion plus sound energy. And some energy is lost to air resistance. It's the kinetic energy that the bullet finally has just before it hits a target that is important.6
Several things can happen when a bullet hits a target. If the bullet stops within the target, it transfers all its kinetic energy to the target, and at the same time it transfers its momentum to the target. It may also pass through the target and emerge at the other side. In this case the bullet transfers some of its kinetic energy and some of its momentum to the target. Finally, it is possible that in the case of a well-armored target, the bullet could bounce back. In this case it delivers all its kinetic energy to the target, but the target actually receives more momentum than the bullet initially had. Because of this, terms such as “knockdown power” and “stopping power,” which are frequently used in terminal ballistics, are actually meaningless. Knockdown power refers to the momentum transfer only, but in reality it is kinetic energy transfer that does the real damage. What happens to a target depends on the details of the collision and which of the above three cases applies, so you can't say a certain type of ammunition (or gun) has a certain knockdown power.
One of the major issues related to terminal ballistics is the penetration of the bullet. A measure of it is given by the impact depth of the bullet, which is the depth the bullet reaches before it is stopped. In some cases bullets are designed to achieve maximum penetration, in others they are designed to do maximum damage. Bullet design is quite different in the two cases. Bullets designed for maximum penetration are made so that they do not deform on impact (or at least, deform as little as possible). They are usually made of lead that is covered with a layer of copper, brass, or steel. The jacket usually covers only the front region of the bullet. In particular, armor-piercing bullets for small arms are usually made of copper jacketed with steel. For larger artillery such as tank guns, tungsten, aluminum, and magnesium are usually used in the shells.
Although some bullets are made to expand when they hit the target, this type of ammunition is now prohibited in warfare according to the Hague Convention of 1899, Declaration III.