Advanced Data Sufficiency Practice Set: Answers and Explanations

  1. A
  2. E
  3. B
  4. A
  5. A
  6. C
  7. C
  8. C
  9. D
  10. B
  11. E
  12. C
  13. D
  14. C
  15. D
  16. B
  17. A
  18. A
  19. B
  20. E
  1. (A)

    If x and y are positive even integers, is (40x)x divisible by y?

    Step 1: Analyze the Question Stem

    This is a Yes/No question. Essentially, the question asks whether is an integer. Note that x and y are both even. Also note that because x is even and 40 is an integer, the expression (40x)x must be even. Finally, note that x is a factor of the base as well as the exponent.

    To determine that y divides evenly into (40x)x, you need to know that y has no prime factors that are not found in 40 or x and that it has no prime factor raised to an exponent that is greater than the number of times that prime number is a factor of (40x)x. If a statement allows you to establish both these conditions, you can answer the question with a yes, and the statement is sufficient. If you can show that either of these conditions does not exist, then the statement allows you to answer the question with a no and is likewise sufficient.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) tells you that y = 128x. Taking this statement into account, the question now becomes whether 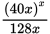is an integer. The number 128 has only 2 as a prime factor, breaking down to 27. So focus on the number of times 2 is a factor of the expression (40x)x. Remember that x is positive and even, so x ≥ 2. Since x is the exponent in the expression (40x)x, a greater value of x will make the number of times 2 is a factor of (40x)x greater. It follows that if x = 2 makes 128x a factor of (40x)x, the answer to the question is definitively yes, and you have sufficiency. (Note that if x > 2, all other factors of x besides 2 will cancel in the denominator because there will be a greater number of them in the numerator due to the exponent. For instance, if x = 6 = (2)(3), then there will be one factor of 3 in the denominator and six factors of 3 in the numerator.)

    Substituting 2 for x yields:

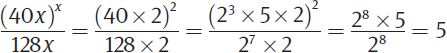
    So x = 2 makes 128x a factor of (40x)x, and Statement (1) is sufficient. Eliminate (B), (C), and (E).

    Statement (2) tells you that y is a multiple of 160 and thus has 2 and 5 as its distinct prime factors. While that may seem to align with the 40 in the exponent, y being a multiple of 160 means that it could be infinitely large and thus potentially too big to be a factor, given that you don’t know the value of x. Statement (2) is insufficient.

    (A) is the correct answer.

  2. (E)

    If a ≠ 0, and is

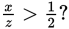
    Step 1: Analyze the Question Stem

    The question stem gives two equations and asks whether a third algebraic fraction is greater than a constant, making this a Yes/No question. You can simplify the given information by combining the two equations. Note that multiplying them together will make the y cancel out: 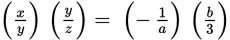results in The question asks about 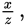so if you can find the values of a and b, you will have sufficiency. You will also have sufficiency if you can find the value of Since 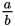is the reciprocal of 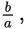you will also have sufficiency if you can find the value of Finally, you will have sufficiency if you can find that, in some other way, there is only one answer to the question regarding and

    Step 2: Evaluate the Statements Using 12TEN

    Since each statement uses only one of the variables needed, (A), (B), and (D) can be crossed off immediately. The task then becomes determining whether the two statements taken together are sufficient or not.

    Neither of the statements is simpler than the other, so begin by factoring either of them. In Statement (1), factoring the left side of the equation a2 − 2a − 3 = 0 yields (a + 1)(a − 3) = 0, making a = −1 or 3. In Statement (2), subtract 1 from both sides, resulting in b2 − 4b + 3 = 0. Factoring the left side of the equation b2 − 4b + 3 = 0 produces (b − 1)(b − 3) = 0, making b = 1 or b = 3.

    As noted in Step 1, in order to answer the question is you must know the values of a and b, or you must know the value 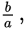or you must know the value 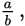or you must be able to compare and 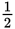in some other way. The four possible combinations of a and b are these:

    a = −1 and b = 1

    a = −1 and b = 3

    a = 3 and b = 1

    a = 3 and b = 3

    Test the first pair, as it is the easiest. If a = −1 and b = 1, then 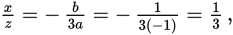which is not greater than 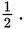In this case, the answer to the question is no.

    To try to avoid having to test all four combinations, notice that with both a and b positive, 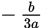will be negative, and the answer will still be no. So stay with a = −1. You can expect a greater value for when b = 3 than when b = 1, so test b = 3. If a = −1 and b = 3, In this case, and the answer to the question is yes.

    One possibility gives you an answer of yes to the question and a different possibility gives you an answer of no to the question, making the statements taken together insufficient to answer the question definitively. The correct answer is (E).

  3. (B)
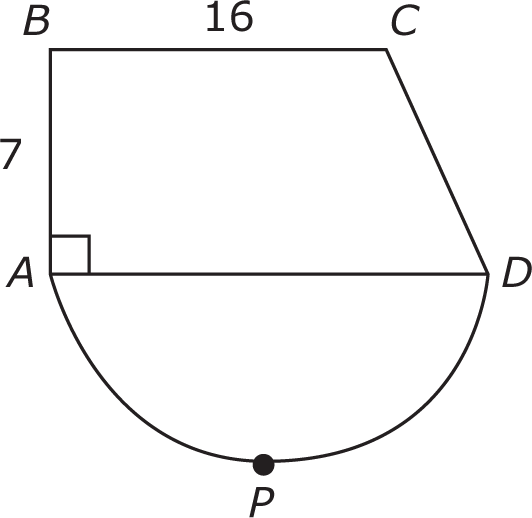
    The diameter AD of semicircle DPA is one side of quadrilateral ABCD. One side adjacent to AD is measure 7, and the side opposite AD is measure 16.

    In the figure above, what is the area of semicircle DPA?

    Step 1: Analyze the Question Stem

    This is a Value question. The question stem contains a diagram with multiple figures, and you need to be able to find a single possible area of the semicircle DPA to have sufficiency. In order to do that, you would need to know the length of diameter AD of the semicircle. AD is also a side of quadrilateral ABCD. Because a semicircle has half the area of a circle with the same diameter, knowing the length of AD would allow you to calculate the area of semicircle DPA.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) tells you that the area of the quadrilateral ABCD is 140. Using the formula for the area of a trapezoid, 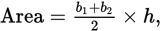it would appear that you could plug in the information you know from the diagram and Statement (1) (the area, the height, and b1) to solve for b2. However, it’s important to remember that figures in Data Sufficiency questions are not necessarily drawn to scale. You are not given enough information to determine whether sides AD and BC are parallel; therefore, ABCD is not necessarily a trapezoid. Statement (1) is thus insufficient, and you can eliminate (A) and (D).

    Statement (2) tells you that the length of the line segment whose endpoints are B and D is 25. This line segment, if added to the figure, would be the hypotenuse of right triangle ABD. Since you now know two sides of a right triangle, it would be possible to calculate the length of the third side, AD, by using the Pythagorean theorem. As mentioned above, knowing the length of AD would allow you to calculate the area of the semicircle, and Statement (2) is sufficient. Therefore, the correct answer is (B).

  4. (A)

    Is x divisible by 39?

    Step 1: Analyze the Question

    This is a Yes/No question. Unlike other remainder questions in which you can pick numbers, the remainders in the statements would be very tedious and time-consuming to test multiple times individually, let alone to combine. Thus, there must be a simpler way to determine divisibility. Whenever the numbers given are unwieldy, the easiest and most efficient way to establish divisibility is to find the prime factors. In this case, 39 breaks down to 3 × 13, so for x to be divisible by 39, it must be divisible by both 3 and 13.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) gives the number 65. Consider that 65 is 5 × 13; one of the prime factors of 39 is present. For x to be divisible by 13, the remainder itself must be a multiple of 13. The remainder 7 is not a multiple of 13, so it is impossible for x to be divisible by 13 or 39. This makes the answer to the question always no, and Statement (1) is sufficient. Eliminate choices (B), (C), and (E).

    In evaluating Statement (2), you can use the same principle. The number 36 is divisible by 3, one of the necessary primes, so the remainder must also be divisible by 3. The remainder 15 is divisible by 3, meaning that x is a multiple of 3. Since you don’t know anything else about x, it’s entirely possible that x is also divisible by 13, while there are certainly values that would make x not divisible by 13. Statement (2) is insufficient.

    The correct answer is (A).

  5. (A)

    If a and b are positive integers with different units digits, and b is the square of an integer, is a also the square of an integer?

    Step 1: Analyze the Question Stem

    This is a Yes/No question. The given information provides a clue about the two numbers having different units digits and tells you that b is a perfect square. On advanced number properties questions, it’s worth checking if two different types of clues work together. Units digits of certain groups of numbers often fall into consistent patterns, and squares certainly fit into that category. The units digits of the squares of 1–10 are {1, 4, 9, 6, 5, 6, 9, 4, 1, 0}, and this pattern will continue, since the units digits of 11–20, 21–30, and so on will be the same as those of 1–10. So a perfect square can only have one of six units digits: 0, 1, 4, 5, 6, or 9. For a to be a perfect square, its units digit must be one of those numbers.

    Step 2: Evaluate the Statements Using 12TEN

    Evaluating Statement (1), you see that the sum of the integers a and b has a units digit of 8. Work your way through the list of possible units digits of squares of integers. Again, that list is 0, 1, 4, 5, 6, and 9. If the units digit of b is 0, then the units digit of a is 8, and 8 is not on the list. If the units digit of b is 1, the units digit of a is 7, and 7 is also not on the list. If the units digit of b is 4, the units digit of a is 4, but this is not permitted because the units digits of a and b must be different. If the units digit of b is 5, the units digit of a is 3, and 3 is not on the list. If the units digit of b is 6, the units digit of a is 2, and 2 is not on the list. If the units digit of b is 9, the units digit of a is 9, but again, the units digits of a and b must be different. It follows that the units digit of a cannot be the units digit of the square of an integer, so a cannot be the square of an integer. The answer to the question is definitively no, and Statement (1) is sufficient. Eliminate (B), (C), and (E).

    Statement (2) precludes a from having 1 as its units digit, but it does nothing else, since the only relevant limitation is that the two numbers have different units digits. Statement (2) is insufficient.

    The correct answer is (A).

  6. (C)

    What is the value of 8x + y?

    Step 1: Analyze the Question Stem

    This is a Value question: a statement that allows the calculation of a single value for 8x + y is sufficient. Simplify the equation in Statement (2):

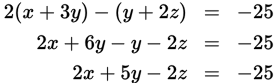
    Step 2: Evaluate the Statements Using 12TEN

    Each of the two statements is an equation with the same three variables. As neither of these equations can be solved for 8x + y, neither statement on its own is sufficient, and you can eliminate (A), (B), and (D).

    Taken together, the two statements represent a system of equations. To solve for each variable in a system of linear equations with three variables, three distinct equations are required. Since the statements provide only two equations, (E) may be tempting. However, even when there are fewer equations than variables, sometimes the value of a particular variable, or the value of an expression, can be found. When a question concerns solving a system of equations for an expression, consider whether multiplying one or both equations by a constant and combining them will allow you to solve. Multiplying the equation in Statement (1) by 2 results in 6x − 4y + 2z = 20. Adding the corresponding sides of this equation and the simplified equation in Statement (2), 2x + 5y − 2z = −25, gives 8x + y = −5. Since both statements together allow the calculation of 8x + y, the correct answer is (C).

  7. (C)

    If b and c are two-digit positive integers and b − c = 22d, is d an integer?

    Step 1: Analyze the Question Stem

    This is a Yes/No question. The question stem tells you that the variables b and c are integers between 10 and 99 inclusive and asks whether b − c is a multiple of 22.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) merely tells you that the two digits of b are the same, so the value of b must be 11, 22, 33, etc. Since you are given no further information about c, Statement (1) by itself is insufficient, and answer (A) and (D) can be eliminated.

    Statement (2) provides the information that b + c is a multiple of 22, since b + c = 22x and x is an integer. However, the question asks about b − c, not b + c, so this statement, too, is insufficient. If you were unsure, you could plug in some number pairs to verify that b − c could be a multiple of 22 but need not be. Set b = 12 and c = 10; b + c = 22, which is divisible by 22, but b − c = 2, which clearly is not divisible by 22. Now try b = 11 and c = 33; b + c = 44 is divisible by 22, while b − c = −22 is divisible by 22 as well. Eliminate (B).

    Now look at both statements together along with the information in the question stem. Statement (1) says that the tens and units digits of b are the same, so b is a multiple of 11. From Statement (2), you know that b + c is a multiple of 22. Every multiple of 22 is a multiple of 11, so b + c is a multiple of 11. Since b + c is a multiple of 11 and b is a multiple of 11, (b + c) − b = c, which is a multiple of 11. Since b and c are both multiples of 11, b − c is also a multiple of 11. Since b + c is a multiple of 22, b + c is even. This means that both b and c are even or both b and c are odd. In either case, b − c is even, or, in other words, b − c is a multiple of 2. Since b − c is a multiple of 11, b − c is a multiple of 2, and the integers 2 and 11 have no common factor greater than 1, b − c is a multiple of 11 × 2 = 22. The statements taken together are sufficient to answer the question definitively yes. (C) is correct.

  8. (C)

    The integers x and y are positive, x > y + 8, and y > 8. What is the remainder when x2 − y2 is divided by 8?

    Step 1: Analyze the Question Stem

    This is a Value question. You are given two positive integers. Since y is an integer and y > 8, the minimum value of y is 9. Since x > y + 8, and the minimum value of y is 9, x must be greater than 9 + 8 = 17. Thus, x > 17. Since x is an integer, the minimum value of x is 18. The question asks for the remainder when the difference of the squares of the two numbers is divided by 8. You can factor the expression x2 − y2 to its equivalent (x + y)(x − y).

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): Since the remainder when x + y is divided by 8 is 7, you can represent x + y as 8m + 7, where m is an integer. Substituting this into the factored expression, (8m + 7)(x − y) still doesn’t tell you enough about x − y to get a definite answer, so Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2): This time, you can substitute 8n + 5 for x − y, where n is an integer, but now you don’t know enough about x + y, so Statement (2) is also insufficient and you can eliminate (B).

    Combining the results above, can you determine with certainty the remainder when (8m + 7)(8n + 5) is divided by 8?

    Using FOIL, you can write the expression (8m + 7)(8n + 5) as 64mn + 40m + 56n + 35. Since the first three terms contain the coefficients 64, 40, and 56, respectively, and m and n are integers, each of these terms is evenly divisible by 8. Thus, the remainder resulting from dividing the expression x2 − y2 by 8 is the remainder when 35 is divided by 8, which is 3. So the statements together are sufficient, and (C) is correct.

  9. (D)

    If x > y > 0, does 3x + 1 + 3(2y) = 12v?

    Step 1: Analyze the Question Stem

    This is a Yes/No question. A statement is sufficient if it allows you to answer the question with either a definite yes or a definite no.

    Begin by simplifying the equation 3x+1 + 3(2y) = 12v. Using the law of exponents that says that babc = ba+c, you can rewrite 3x+1 as (3x)(31) = 3(3x). So replace 3x+1 with 3(3x): 3(3x) + 3(2y) = 12v. Now factor a 3 out of the left side to yield 3(3x + 2y) = 12v. Dividing both sides of the equation by 3 results in 3x + 2y = 4v. So the question stem is asking, “If x > y > 0, does 3x + 2y = 4v?”

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): Rewrite the equation to evaluate it. There is a law of exponents that says that (ba)c = bac, so 32x = (3x)2 and 22y = (2y)2. It follows that 32x − 22y = (3x)2 − (2y)2. This is one of the classic quadratics: (3x)2 − (2y)2 = (3x − 2y)(3x + 2y). So Statement (1) can be written as 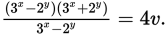Cancel a factor of 3x − 2y from the numerator and denominator of the left side of the equation to find that 3x + 2y = 4v. Since 3x + 2y = 4v is equivalent to 3x+1 + 3(2y) = 12v, Statement (1) allows you to answer the question with a definite yes and is sufficient. Eliminate (B), (C), and (E).

    Statement (2): Because babc = ba+c, 3x+2 = (3x)(32) = (3x)(9) = 9(3x). Also, 2y+1 = (2y)(21) = (2y)(2) = 2(2y). Thus, 2(3x+2) + 9(2y+1) = 72v can be written as 2[9(3x)] + 9[2(2y)] = 72v, or 18(3x) + 18(2y) = 72v. Factoring 18 out of the left side of the equation gives 18(3x + 2y) = 72v. Divide both sides of the equation by 18: 3x + 2y = 4v. Since this is the same equation shown to be sufficient for Statement (1), Statement (2) allows you to answer the question with a definite yes and is sufficient.

    (D) is correct.

  10. (B)
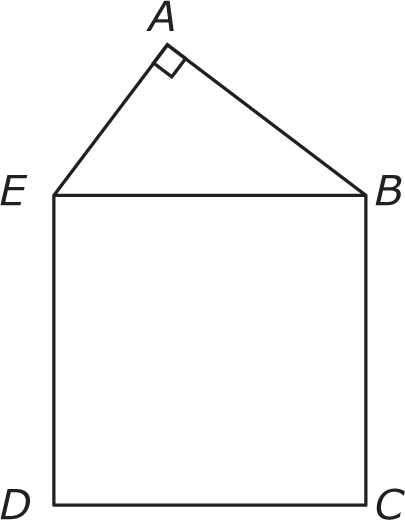
    The hypotenuse of right triangle ABE is also side EB of square BCDE.

    In the figure above, the measure of angle EAB in triangle ABE is 90 degrees, and BCDE is a square. What is the length of AB?

    Step 1: Analyze the Question Stem

    This is a Value question. The figure shows a right triangle whose hypotenuse is one side of a square, and a statement that is sufficient would allow you to find the length of side AB.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): The area of right triangle ABE is

    Since triangle ABE is a right triangle, the Pythagorean theorem says that (BE)2 = (AB)2 + 122 = (AB)2 + 144. Thus, 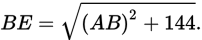The area of square BCDE is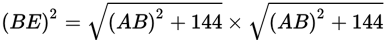

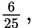
    Since the ratio of the area of triangle ABE to the area of square BCDE is Solve this equation for AB: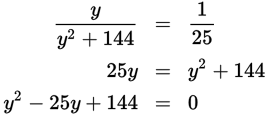

    Factor y2 − 25y + 144. With some testing, you find that y2 − 25y + 144 = (y − 9)(y − 16). So (y − 9)(y − 16) = 0. Thus, it is possible that the length of AB is 9 or 16. Because more than one answer to the question is possible, Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2): The perimeter of square ABCD is 80, so the length of one side of the square is Because the ratio of AE to AB is 3 to 4, right triangle ABE is a 3-4-5 right triangle. Knowing the ratios of the sides and the length of the hypotenuse, you could calculate the length of side AB. However, since this is a Data Sufficiency question, there is no need to perform the calculations. Statement (2) is sufficient. (For the record, right triangle ABE has side lengths of 12, 16, and 20. AB is the longer leg and equals 16.)

    (B) is correct.

  11. (E)

    In the sequence T, the first term is the non-zero number a, and each term after the first term is equal to the non-zero number r multiplied by the previous term. What is the value of the fourth term of the sequence?

    Step 1: Analyze the Question Stem

    This is a Value question involving a geometric sequence. Each term after the first term is r times the previous term. So if the nth term is an, where n is an integer and n ≥ 1, then a1 = a, a2 = ar, a3 = ar2, a4 = ar3, a5 = ar4, and so on. In general, if n is an integer and n ≥ 1, then the nth term is the product of one factor of a and n − 1 factors of r, or an = arn−1.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): The sum of the first two terms is 16. Thus, a + ar = 16. This is one equation with two variables, and there are many possible values for a and r. Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2): This statement says that a18 = 81a14. You know the following:

    a15 = a14r

    a16 = a15r

    a17 = a16r

    a18 = a17r

    So a18 = a17r = (a16r)r = a16r2 = (a15r)r2 = a15r3 = (a14r)r3 = a14r4.

    Since a18 = 81a14, a14r4 = 81a14. According to the question stem, a ≠ 0 and r ≠ 0, so a14 does not equal 0. Divide by a14: r4 = 81. Now 81 = 34 or (−3)4, so r = 3 or r = −3. This statement provides two values for r and no information about a, so the fourth term cannot be calculated. For example, if a = 4 and r = 3, then a4 = 4(34 − 1) = 4(33) = 4(27) = 108. But if a = 2 and r = −3, then a4 = 2(−3)4 −1 = 2(−3)3 = 2(−27) = −54. Since different answers to the question are possible, Statement (2) is insufficient. Eliminate (B).

    The statements taken together: From Statement (1), which says that the sum of the first two terms is 16, you know that a + ar = 16. From Statement (2), which says that a18 = 81a14, you know that r = 3 or r = −3.

    Consider the case where r = 3. Substituting 3 for r into the equation a + ar = 16, a + a(3) = 16, a + 3a = 16, 4a = 16, and a = 4. In this case, the fourth term is ar4−1 = 4(34−1) = 4(33) = 4(27) = 108. Now consider the case where r = −3. Substituting −3 for r into the equation a + ar = 16, a + a(−3) = 16, a − 3a = 16, −2a = 16, and a = −8. With these values of r and a, the fourth term is (−8)(−3)4−1 = (−8)(−3)3 = (−8)(−27) = 216. Because there is more than one possible answer to the question, the statements taken together are insufficient.

    (E) is correct.

  12. (C)

    A person is to be selected at random from the group T of people. What is the probability that the person selected is a member of club E?

    Step 1: Analyze the Question Stem

    This is a Value question involving the probability of a single event. A person is to be selected at random from group T, and the question asks for the probability that the person selected is a member of club E. The probability that the person selected is a member of club D can be written as P(D) and the probability that the person is a member of club E as P(E).

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): The probability that the person selected is not a member of either club is The probability that an event does not occur is equal to 1 minus the probability that the event does occur, so the probability that the person chosen is a member of at least one of the two clubs—that is, P(D or E)—is 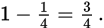In general, P(D or E) = P(D) + P(E) − P(D and E). (This formula is worth memorizing.) In this case, you can substitute for P(D or E), so 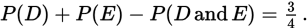However, without any other information about P(D) or P(D and E), you cannot find P(E). Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2): Because the probability that the chosen person is a member of club D and not club E is Since P(D) = P(D and E) + P(D and not E), P(D and not E) = P(D) − P(D and E). Thus, 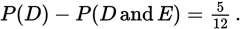There is no way to find P(E) from this information. Statement (2) is insufficient, and (B) can be eliminated.

    The statements taken together: from Statement (1), From Statement (2), You can rearrange the equation from Statement (1): Using substitute for P(D) − P(D and E) in Then and you can solve for the probability that the person selected is a member of club E. There is no need to do the calculation, but for the record, it would be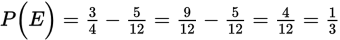

    The statements taken together are sufficient.

    (C) is correct.

  13. (D)

    The population of Town X on January 1, 2010, was 56 percent greater than the population of the same town on January 1, 2005. The population of Town X on January 1, 2015, was 75 percent greater than the population of the same town on January 1, 2010. What was the population of Town X on January 1, 2005?

    Step 1: Analyze the Question Stem

    This is a Value question involving multiple percent increases. Say the population of Town X on January 1, 2005, was N. Because the population of Town X on January 1, 2010, was 56% greater than the population on January 1, 2005, the population in 2010 was N + (56% of N) = N + 0.56N = 1.56N. Then because the population on January 1, 2015, was 75% greater than the population on January 1, 2010, the population in 2015 can be written as follows:

    Note that because you know the percent increase from each of the three named years to the next, a statement that provides the population for any of those three years will be sufficient.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): Because the population on January 1, 2015, was 2.73N, you can write the equation 2.73N = 21,840. Then This equation produces just one value for N, so Statement (1) is sufficient. Eliminate (B), (C), and (E).

    Statement (2): The increase in the population from 2005 to 2010 can be written as 1.56N − N = 0.56N. The increase in the population from 2010 to 2015 is 2.73N −1.56N = 1.17N. Because the increase from 2010 to 2015 was 4,880 greater than the increase from 2005 to 2010, you can write the equation 1.17N = 0.56N + 4,880. There is one equation with one variable, so you could solve for N and Statement (2) is sufficient.

    (D) is correct.

  14. (C)

    What is the value of x − 3z?

    Step 1: Analyze the Question Stem

    This is a Value question. Knowing the values of x and z separately would be sufficient to answer the question, as would knowing the value of the entire expression x − 3z.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) is clearly insufficient, as the equation x + 4y = 3 does not include the variable z. Eliminate (A) and (D).

    Statement (2) provides one equation with three variables, so there will be different possible values for x − 3z. For example, if you let x = 0 and y = 8, then the equation x2 + 4xy − 3xz − 12yz = 24 leads to Plugging x = 0 and into x − 3z, you have In this case, the answer to the question is 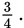But if you let x = 3 and y = 0, the equation x2 + 4xy − 3xz − 12yz = 24 leads to Plugging x = 3 and into x − 3z gives you the following: 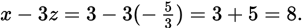In this case, the answer to the question is 8. Since different answers to the question are possible, Statement (2) is insufficient. Eliminate (B).

    To combine the statements, start by simplifying the left side of the equation in Statement (2):

    x2 + 4xy − 3xz − 12yz = x(x + 4y) − 3z(x + 4y) = (x + 4y)(x − 3z)

    Thus, Statement (2) is equivalent to (x + 4y)(x − 3z) = 24. Statement (1) says that x + 4y = 3. Substitute 3 for x + 4y in the equation (x + 4y)(x − 3z) = 24 to produce 3(x − 3z) = 24. Dividing both sides by 3 yields x − 3z = 8. The statements together lead to a single possible value of 8 for x − 3z. The statements taken together are sufficient.

    (C) is correct.

  15. (D)
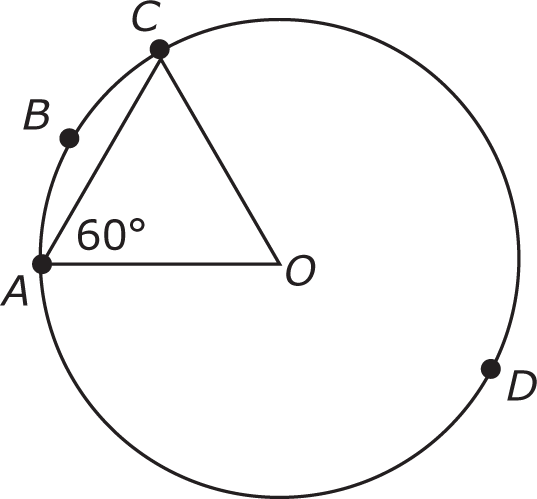
    Triangle OAC lies within a circle such that vertex O is also the center of the circle and vertices A and C lie on the circumference of the circle. The measure of angle A is 60 degrees. Arc ABC is defined by the central angle AOC. Point D lies on the circumference of the circle outside arc ABC.

    In the figure above, the center of the circle is O, and the measure of angle CAO is 60 degrees. What is the perimeter of triangle OAC?

    Step 1: Analyze the Question Stem

    This question asks for the perimeter of the triangle, so it is a Value question. Sides OA and OC of triangle OAC are both radii of the circle, so OA = OC, making the triangle isosceles, so that ∠OCA must also equal 60°. Because the three angles of a triangle must sum to 180°, the central angle is also 60°—in other words, triangle OAC is equilateral. So each of its three sides is equal to the circle’s radius. If you can find the radius, you can find the perimeter of the triangle, and you have sufficiency.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): In a circle with radius r, the length L of an arc intercepted by a central angle whose measure is n degrees is given by the formula Here, the central angle intercepting arc CDA has a measure of 360° − 60° = 300°, and the central angle intercepting arc ABC has a measure of 60°. So the length of arc CDA is 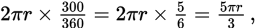and the length of arc ABC is 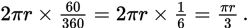Since Statement (1) says that the length of arc CDA is 16π greater than the length of arc ABC, you know that That’s a single equation in one variable, so you can solve for r. Statement (1) is sufficient. (For the record, dividing both sides of this equation by π and multiplying both sides by 3 yields 5r = r + 48, so r = 12, and the perimeter is 3(12) = 36.) Eliminate (B), (C), and (E).

    Statement (2) says that the area of triangle OAC is Triangle OAC is equilateral. Call the length of each side of triangle OAC s.

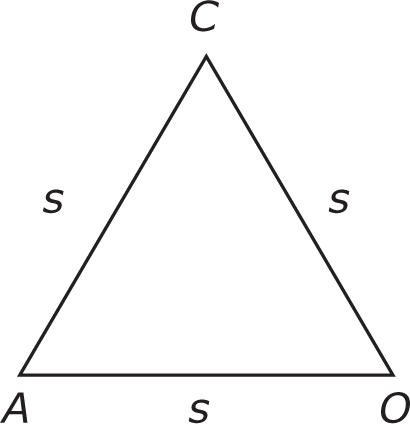
    Triangle OAC is shown by itself. Each side is labeled length s.

    Drop an altitude from point C to side OA:

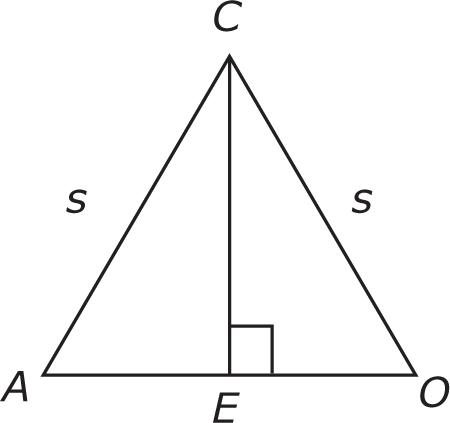
    Triangle OAC is shown with an altitude dropped from vertex C to point E on the base, forming a right angle.

    Altitude CD divides triangle OAC into 2 identical 30°-60°-90° degree right triangles.

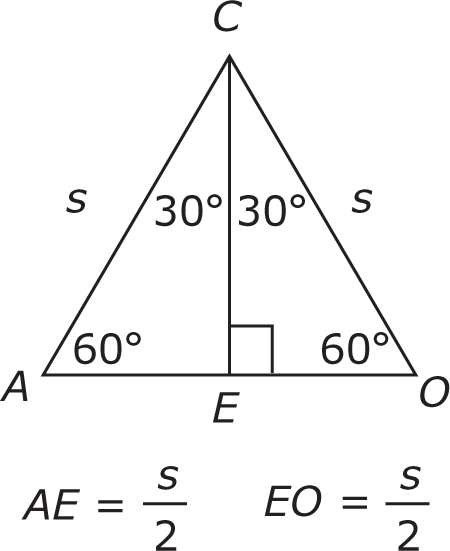
    Triangle OAC is bisected into two right triangles by an altitude from vertex C to point E. At the base, angle A measures 60 degrees, and angle O measures 60 degrees. At the top, angle ACE measures 30 degrees, and angle ECO measures 30 degrees. The base is bisected into segment AE and segment EO, both of which measure one-half s.

    The 2 identical 30°-60°-90° degree right triangles are triangles ACE and OCE. The side lengths in a 30°-60°-90° degree right triangle are in a ratio of 1 to 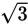to 2. Since the length of hypotenuse AC of right triangle ACE is s, the length of leg AE, which is opposite the 30-degree angle must be and the length of leg CE, which is opposite the 60-degree angle, must be 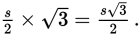You can now describe the area of triangle OAC in terms of s. The area of any triangle is Call the base is OA and the height CE. Then OA = s and The area of triangle OAC is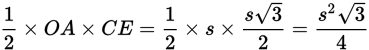

    Since the area of triangle OAC is given in Statement (2) to be you can write the equation 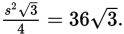That’s again a single equation in one variable. It does have a squared term, but as negative lengths are disallowed, you can stop here and declare Statement (2) sufficient. (For the record: 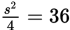so s2 = 144 and s = 12. The perimeter is again 3(12) = 36.)

    (D) is correct.

  16. (B)

    If x and y are integers and 3x > 8y, is y > −18?

    Step 1: Analyze the Question Stem

    This is a Yes/No question with two integer variables. Simplify the inequality given in the stem, 3x > 8y, to get .

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): The possible values of x are limited by the range of this inequality, so examine the endpoints of the range. If x > −9, the least value that is permissible for x is −8. Since y is less than it follows that y < −3. Some values of y could be > −18, but there is no lower limit for y, so it could also be < −18. There is no need to evaluate the upper boundary of x. Statement (1) is insufficient, so eliminate (A) and (D).

    Statement (2): Simplify the equation by multiplying both sides by 5 to get 5y = x − 42. Add 42 to both sides and x = 5y + 42. Substitute this value for x into the inequality 3x > 8y:

    Statement (2) is sufficient to answer definitively yes.

    (B) is correct.

  17. (A)

    Over the course of 5 days, Monday through Friday, Danny collects a total of 76 baseball cards. Each day, he collects a different number of cards. If Danny collects the largest number of cards on Friday and the second largest number of cards on Thursday, did Danny collect more than 8 cards on Thursday?

    Step 1: Analyze the Question Stem

    This is a Yes/No question that is packed with information in the stem. Danny collects a different number of cards each of the 5 days. He collects the largest number of cards on Friday and the second largest number on Thursday. The question asks if Danny collected more than 8 cards on Thursday.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): The largest number of cards collected on Thursday that would result in a no answer to the question is 8. Since the number of cards collected Monday, Tuesday, and Wednesday is different each day and must be less than 8, the maximum numbers of cards he could collect on those days are 5, 6, and 7. Totaling up all the days, 5 + 6 + 7 + 8 + 49 = 75. Collecting 8 cards on Thursday does not enable Danny to collect 76 cards in total given the constraints of the question, so the information in Statement (1) means that Danny must have collected more than 8 cards on Thursday. Statement (1) is sufficient to answer “always yes,” so eliminate (B), (C), and (E).

    Statement (2): If Danny collects 6 cards on one of the first 3 days, the fewest cards he could have collected on those days would be 6 + 2 + 1 = 9, leaving 76 − 9 = 67 cards to be collected on Thursday and Friday. Danny could have collected 7 cards on Thursday and 60 on Friday, in which case the answer to the question is no. Alternatively, he could have collected as many as 33 cards on Thursday and 34 on Friday and the answer would be yes. Therefore, Statement (2) is insufficient.

    (A) is correct.

  18. (A)

    If y = x2, is the equation (25y)(4120) = 1620x true?

    Step 1: Analyze the Question Stem

    This question asks whether an equation is true, making it a Yes/No question. Start by simplifying the equation in the question stem. Notice that you can write all three powers with a base of 2, since 4 = 22 and 16 = 24. Substituting these values produces (25y)((22)120) = (24)20x, which simplifies to (25y)(22 × 120) = 24 × 20x, or (25y)(2240) = 280x. This, in turn, can be rewritten as 25y + 240 = 280x. When equal powers have the same base, the exponents must be equal. So 5y + 240 = 80x. Remember that y = x2, so you can substitute x2 for y to yield 5x2 + 240 = 80x. Subtracting 80x from both sides, 5x2 − 80x + 240 = 0. Dividing both sides by 5, x2 − 16x + 48 = 0. This factors to (x − 4)(x − 12) = 0. So x − 4 = 0 or x − 12 = 0, and x = 4 or x = 12.

    So if x = 4 or x = 12, then the equation (25y)(4120) = (1620x) is true, and the answer to the question is definitively yes. If x is neither of these values, the answer is definitively no. Either of these situations would be sufficient.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) says that (4 − x)(12 − x) = 0. When the product of a group of numbers is 0, at least one of the numbers must be 0. So if (4 − x)(12 − x) = 0, then 4 − x = 0 or 12 − x = 0. If 4 − x = 0, then 4 = x, or x = 4. If 12 − x = 0, then 12 = x, or x = 12. You’ve already determined that the equation (25y)(4120) = (1620x) is true when x = 4 or x = 12. Statement (1) is sufficient, as the answer to the question is always yes. Eliminate (B), (C), and (E).

    Statement (2) says that (x − 4)(x − 8)(x − 24) = 0. Again, when the product of a group of numbers is 0, at least one of the numbers must be 0. So in this case, x − 4 = 0, x − 8 = 0, or x − 24 = 0. If x − 4 = 0, then x = 4. If x − 8 = 0, then x = 8. If x − 24 = 0, then x = 24. The possible values of x are 4, 8, and 24. You know that the equation (25y)(4120) = (1620x) is true when x = 4 or x = 12. If x = 4, then the answer to the question is yes. If x = 8, or if x = 24, the answer to the question is no. Since more than one answer to the question is possible, Statement (2) is insufficient.

    (A) is correct.

  19. (B)

    The ratio of the number of students in an auditorium who are seniors to the number of students in the auditorium who are not seniors is 7:5. How many students are there in the auditorium?

    Step 1: Analyze the Question Stem

    This is a Value question. Since the question asks for the total number of students, start by rewriting the part to part ratio in the question stem as a part to whole ratio. The ratio of seniors to non-seniors is 7:5, so the ratio of the students who are seniors to the total number of students is 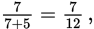and the ratio of the students in the auditorium who are not seniors to the total number of students is Remember that there is a common multiplier in the numerator and denominator of every ratio, so you could write the ratio of seniors to total students as 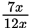and the ratio of non-seniors to total students as 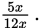If you can find the common multiplier x, you can find the total number of students, and you have sufficiency.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): You are given the ratio of the number of students who are seniors who are taking history to the number of students who are not seniors who are taking history. There is no actual number of students given, and no way to calculate the common multiplier in the original ratio and thus calculate the total number of students. Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2): From the ratio given in the question stem, you know that there are 7x seniors, 5x non-seniors, and 12x total students present in the auditorium. From Statement (2), you know that of the 7x seniors, are taking history. In other words, seniors are taking history. Similarly, of the 5x non-seniors are taking history, so non-seniors are taking history. Furthermore, the number of seniors taking history is 208 greater than the number of non-seniors taking history, so you can write an equation to solve for x: This is a single equation in one variable, so you can stop here and declare Statement (2) to be sufficient. (For the record: 21x = 5x + 208(5), 16x = 208(5), x = 13(5) = 65. There are 12x = (12)(65) = 780 total students.)

    (B) is correct.

  20. (E)

    If y > 0, is

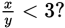
    Step 1: Analyze the Question Stem

    Since y is positive, you can multiply both sides of the inequality by the positive number y to obtain the equivalent inequality x < 3y. So the question is equivalent to “If y > 0, is x < 3y?”

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): Factor x + y out of the left side of the inequality to yield x(x + y) − 4y(x + y) = (x + y)(x − 4y). So Statement (1) is equivalent to (x + y)(x − 4y) < 0. When the product of two quantities is negative, one of the quantities must be negative and the other quantity must be positive. So either (i) x + y < 0 and x − 4y > 0, or (ii) x + y > 0 and x − 4y < 0. (Keep in mind that y is positive.) In case (i), if x + y < 0, then x < −y. If x − 4y > 0, then x > 4y. So in case (i), x < −y and x > 4y. Since y is positive, x < −y means that x is less than −y, where −y is a negative number. Since y is positive, x > 4y means that x is greater than 4y, where 4y is a positive number. So case (i) requires that x be less than the negative number −y and also requires that x be greater than the positive number 4y. This is impossible. So case (i), which is x + y < 0 and x − 4y > 0, cannot happen. On to case (ii), which is x + y > 0 and x − 4y < 0. (Again, keep in mind that y > 0.) If x + y > 0, then x > −y. If x − 4y < 0, then x < 4y. So this time, x > −y and x < 4y. Since y is positive, x > −y means that x is greater than the negative number −y. Since y is positive, x < 4y means that x is less than the positive number 4y. So case (ii), x + y > 0 and x − 4y < 0, is possible. In case (ii), you can conclude that −y < x < 4y. Because case (i) is impossible, Statement (1) is equivalent to −y < x < 4y. Since y is positive, 3y < 4y. You know that x < 4y. However, you do not know whether or not x < 3y.

    More than one answer to the question is possible, so Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2): Simplify the inequality 5(y + 8) < 20y − 3x + 40.

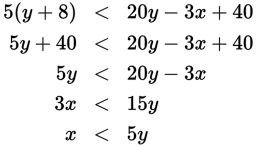
    Statement (2) is equivalent to x < 5y. Since y is positive, 3y < 5y. You know that x < 5y. However, you do not know whether or not x < 3y. Statement (2) is insufficient. Eliminate (B).

    The statements taken together: Statement (1) is equivalent to −y < x < 4y and Statement (2) is equivalent to x < 5y. Because the question requires that y > 0, 4y < 5y and the range in Statement (1) is a subset of the range in Statement (2). Therefore, the statements taken together require that −y < x < 4y, which you have already determined to be insufficient.

    (E) is correct.