Averages

The average (arithmetic mean) of a group of numbers is defined as the sum of the values divided by the number of values.

Example: Henry buys 3 items costing $2.00, $0.75, and $0.25. What is the average price?

Balanced Average: You can save yourself a lot of laborious and error-prone calculation if you think of the average as a “balancing point” between the numbers in the series. That is, the difference between the average and every number below it will equal the difference between the average and every number above it. The “balanced average” approach dramatically reduces the difficulty of the arithmetic.

You’ve already seen that the average of $2.00, $0.75, and $0.25 is $1.00. Here’s how that balances:

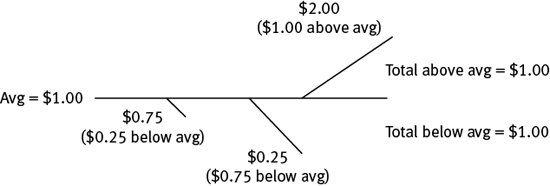
Now let’s use this approach to solve a problem.

Example: The average of 43, 44, 45, and x is 45. What is the value of x?

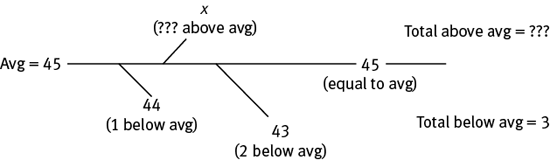
Since the amount above the average must equal the amount below the average, the amount above must be 3. Therefore x is 3 above the average: 3 + 45 = 48; x = 48.

Weighted Average: A further way to calculate averages on the GMAT is to use the “weighted average” formula:

Weighted average of n terms = (Percent₁)(Average₁) + (Percent₂)(Average₂) + . . . + (Percent_n)(Average_n)

Weighted averages are useful when you know the average of different portions of the whole. For example, if two-fifths of the students in a class have a GPA of 79 and the remaining three-fifths have an average of 84, you could set up the weighted average formula as follows:

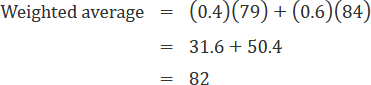
Notice the average of the whole class comes out to be closer to 84 than to 79. This will always be the case when the portions of the whole are of different sizes. In fact, this is where the term “weighted average” comes from; the larger the portion of the whole, the more heavily “weighted” that portion is when calculating the overall average. Note that you can use the weighted average formula as long as you have averages for all portions adding up to 100 percent of the whole.

In-Format Question: Averages on the GMAT

Now let’s use the Kaplan Method on a Data Sufficiency question dealing with averages:

1. If each of the bowlers in a tournament bowled an equal number of games, what is the average (arithmetic mean) score of all the games bowled in the tournament?
   1. Of the bowlers, 70% had an average (arithmetic mean) score of 120, and the other 30% had an average score of 140.
   2. Each of the 350 bowlers in the tournament bowled 3 games.

Step 1: Analyze the Question Stem

First, determine the type of Data Sufficiency question you’re dealing with. You need one exact value for the average score of the games, so this a Value question.

There’s no direct simplification to be done, but the fact that you’re asked for an average should alert you to the possibility that you can get the answer in a variety of ways—either through direct calculation of the scores or through a weighted average approach.

To answer the question, you’ll need either the number of games and the total of the scores or some way to calculate a weighted average.

Step 2: Evaluate the Statements Using 12TEN

Statement (2) is very straightforward, so starting there makes sense. This tells you the number of games but nothing about the scores. Insufficient. Eliminate (B) and (D).

Statement (1) doesn’t allow you to figure out exactly the number of games or the exact sum of the scores. But since the proportions add up to 100% of the total, and since all the bowlers bowled the same number of games, you can calculate the overall average using the weighted average approach. Sufficient. The answer is (A).

Remember, you don’t actually want to calculate the average, just know that you could. That calculation would be: overall average = 0.7(120) + 0.3(140).

The GMAT rewards those who think critically and find the most efficient approach to a problem. By using the weighted average approach, you avoided messy calculations and saved valuable time.

Takeaways: Averages

• .
• Balanced average approach: the sum of the differences between each term and the average must be zero. You can solve some average questions using this fact alone.
• Weighted average of n terms = (Percent₁)(Average₁) + (Percent₂)(Average₂) + . . . + (Percent_n)(Average_n).

Practice Set: Averages on the GMAT

1. Jerry’s average (arithmetic mean) score on the first 3 of 4 tests is 85. If Jerry wants to raise his average by 2 points, what score must he earn on the fourth test?
   1. 87
   2. 89
   3. 90
   4. 93
   5. 95
2. The average (arithmetic mean) of all scores on a certain algebra test was 90. If the average of the 8 male students’ grades was 87, and the average of the female students’ grades was 92, how many female students took the test?
   1. 8
   2. 9
   3. 10
   4. 11
   5. 12
3. An exam is given in a certain class. The average (arithmetic mean) of the highest score and the lowest score on the exam is equal to x. If the average score for the entire class is equal to y and there are z students in the class, where z > 5, then in terms of x, y, and z, what is the average score for the class, excluding the highest and lowest scores?
   1. 
   2. 
   3. 
   4. 
   5. 

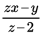
4. The average price of Emily's 5 meals was $20. Meals with a price of $25 or more include a free dessert. How many of Emily's 5 meals included a free dessert?

   1. The most expensive of the 5 meals had a price of $50.
   2. The least expensive of the 5 meals had a price of $10.