Answers and Explanations

1. D
2. E
3. D
4. C
5. C
6. E
7. B
8. E
9. B
10. D
11. C
12. A
13. C
14. A
15. A
16. B
17. E
18. B
19. C
20. A

1. (D)

   Step 1: Analyze the Question

   Jerry has an 85 average after 3 exams. After his fourth exam, he wants an overall average of 87.

   Step 2: State the Task

   Find the score Jerry must earn on his fourth exam to achieve an overall average of 87.

   Step 3: Approach Strategically

   The quickest way to solve this problem is to use the “balanced average” approach. To earn an overall average of 87 on 4 exams, Jerry needs his fourth test to be an 87 plus the number of points that his other 3 tests were “deficient” with respect to this goal. You know that the average of the first 3 exams was a score of 85, so each of those 3 exams, on average, falls short by 87 − 85 = 2 points. Therefore, Jerry needs a score of 87 + 2 + 2 + 2 = 93 on his fourth exam. (D) is correct.

   Step 4: Confirm Your Answer

   To confirm your answer, you can backsolve by plugging (D) back into the question: if Jerry scores 85, 85, 85, and 93 on his 4 exams, that’s an average of . This confirms that (D) is correct.

2. (E)

   In most questions dealing with averages, you should consider picking numbers, setting each term in a group equal to the average of that group. You’ll see in Step 3 how doing so allows you to perform efficient solutions.

   Step 1: Analyze the Question

   Eight male students take a test, and an unknown number of female students take the test. This question gives you lots of information about averages. Don’t rush to set up algebra yet, as there may be a more efficient approach.

   Step 2: State the Task

   Figure out how many female students took the test. Call that number f.

   Step 3: Approach Strategically

   This would be a very straightforward backsolving question, as you could just test an answer choice and see whether it’s consistent with the rest of the information in the question stem. But first, look at a quick math-based approach, taking advantage of the rapid calculations permitted by the “balanced average approach.”

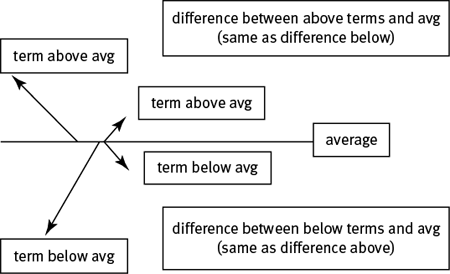
   The “balanced average approach” takes advantage of the fact that the sum of the differences between the terms and the average must be zero. Phrased another way, the total amount by which the terms above the average are larger than the average must equal the total amount by which the terms below the average are smaller than the average:

   

   For this problem, here’s how it works: since the only restrictions are that the male students’ scores must average to 87 and that the female students’ scores must average to 92, you can pick numbers and set all 8 male scores equal to 87 and all female scores equal to 92.

   

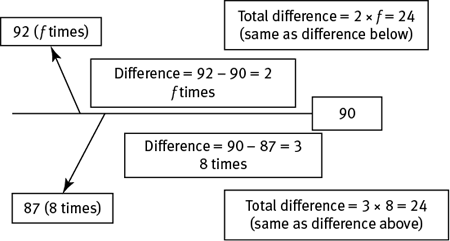
   This approach gives you an equation to solve for f.

   2f = 24

   f = 12

   The answer is (E).

   Now, try the question using backsolving. Say that you started with (D). If there were 11 female students whose scores averaged 92, then

   Average =

   92 =

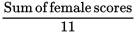
   92 × 11 = Sum of female scores

   1,012 = Sum of female scores

   The men’s scores are given:

   87 =

   87 × 8 = Sum of male scores

   696 = Sum of male scores

   You can set up the formula for the average of the whole group as follows:

   Average =

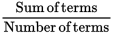
   Average =

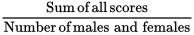
   Average =

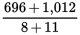
   Average =

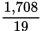
   Average =

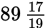
   But the average is supposed to be 90. You’re too low, so you need more female students’ scores to pull the average up. (E) must be correct.

   And here’s the algebraic approach:

   Average =

   Average =

   90 =

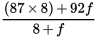
   90 × (8 + f) = (696) + 92f

   (90 × 8) + 90f = 696 + 92f

   720 + 90f = 696 + 92f

   720 − 696 = 92f − 90f

   24 = 2f

   12 = f

   The balanced average approach almost always permits fewer steps and easier calculations.

   Step 4: Confirm Your Answer

   Reread the question stem, making sure that you didn’t miss any important information in the problem.

3. (D)

   Step 1: Analyze the Question

   This is a very complicated word problem, with lots of variables, including variables in the answer choices. Whenever there are variables in the answer choices, consider picking numbers. When picking numbers in a question dealing with averages, pick all the numbers in a group to equal the average of that group.

   Step 2: State the Task

   Your task is to calculate the average of the class after excluding the highest and lowest scores. Before rushing into the math, think logically about what the task tells you about the correct answer. Since the total size of the class is z, there will be (z − 2) scores after the high score and low scores are eliminated. Since an average is the sum divided by the number of terms, the correct answer must have (z − 2) as a denominator. A quick check of the answer choices reveals that only (C) and (D) might possibly be correct. If you were falling behind on time or unsure of how to approach this question, you could make a 50/50 guess pretty quickly.

   Many GMAT word problems have answer choices that can be eliminated without much math.

   Step 3: Approach Strategically

   See what you know about the class. The average of the whole class is y, and there are z students in the class. Now what about the high and low scores? You’re told nothing about them, save that their average is x.

   This is all pretty abstract, so simplify things by picking numbers. Start with the number of students. It must be greater than 5, so say that it’s 6 (z = 6).

   Now pick scores for the 6 students. You could pick all different scores, but the easiest approach of all is to let all 6 scores be equal to the average of those scores. Say that the class as a whole averages a score of 2. After all, “realism” doesn’t matter when picking numbers, only permissibility and manageability. So y = 2.

   scores (in order): 2, 2, 2, 2, 2, 2

   Now, what are the highest and the lowest? Let’s bold them below for emphasis:

   scores (in order): 2, 2, 2, 2, 2, 2

   Together, the high and low scores also average 2. We can calculate that so quickly because when all the terms in a group equal the same value, the average is also equal to that value. So x = 2.

   Your task is to calculate the average of the class after excluding the high and low scores:

   scores (in order): 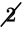, 2, 2, 2, 2,

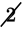
   Looks like that average will be 2 as well. Now you just need to plug z = 6, y = 2, and x = 2 into the answer choices, looking for the result of 2:

   (A)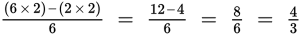. Eliminate.

   (B). Eliminate.

   (C)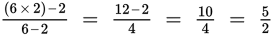. Eliminate.

   (D)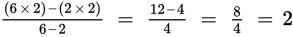. Possibly correct.

   (E)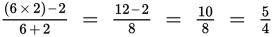. Eliminate.

   The answer is (D).

   There is an algebraic solution, but you may find this approach more complicated and abstract:

   Average of non-excluded scores =

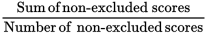
   Number of non-excluded scores = Number of all scores − Number of excluded scores

   Number of non-excluded scores = z − 2

   Sum of non-excluded scores = Sum of all scores − Sum of excluded scores

   Average of all scores =

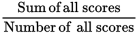
   y =

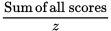
   zy = Sum of all scores

   Average of excluded scores =

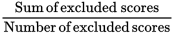
   x =

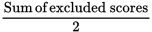
   2x = Sum of excluded scores

   Sum of non-excluded scores = zy − 2x

   Average of non-excluded scores =

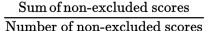
   Average of non-excluded scores =

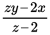
   This expression matches (D), which is the correct answer.

   Picking numbers can reduce some of the most complicated average questions to very simple arithmetic.

   Step 4: Confirm Your Answer

   Reread the question stem, making sure that you didn’t miss anything about the problem.

4. (C)

   Step 1: Analyze the Question Stem

   This is a Value question. Since the average price of Emily's 5 meals was $20, the sum of the prices of all 5 meals was 5 × $20 = $100. You're also told that meals with a price of $25 or more include a free dessert. You need to determine whether there's enough information to find how many of Emily's meals included a free dessert. Thus, you'll have sufficient information if you can determine the exact number of meals that had a price of at least $25.

   Step 2: Evaluate the Statements Using 12TEN

   Look at Statement (1). The most expensive meal had a price of $50, and the sum of all 5 prices was $100, so the prices of the other 4 meals must have had a sum of $100 − $50 = $50. However, there's no way to determine how that $50 was distributed among the remaining 4 meals; it could be that 1 of the meals was $25 or more and each of the other 3 was less than $25, or it could be that each of the 4 meals was less than $25. Because there's insufficient information in this statement to determine an exact number of meals costing $25 or more, eliminate (A) and (D).

   Statement (2) tells you that the least expensive of the 5 meals had a price of $10. Since the prices of the 5 meals sum to $100, the prices of the 4 most expensive meals sum to $90. Now, consider the possibilities: it could be that 3 of these 4 meals are $25 each and the 4th is $15, or that 1 meal is $45 and the other 3 are $15 each, or some other combination of prices that sum to $90. Since there is more than one possibility for the number of meals that cost at least $25, this statement is insufficient. Eliminate (B).

   Now, consider the statements together. If the most expensive meal were $50 and the least expensive meal were $10, then the sum of the remaining 3 meals was $100 − $50 − $10 = $40. How might this $40 be distributed among the remaining 3 meals? Since Emily's least expensive meal was $10, each of these 3 remaining meals must cost more than $10, so 2 of the 3 together must cost over $20; therefore, the third cannot be as much as $25 (for example, if 2 of these 3 remaining meals were $10.50 each, there would only be $40 − $10.50 − $10.50 = $19 left for the third meal). Therefore, it's only possible for 1 meal (the most expensive, $50 one) to have a price of at least $25. Thus, the two statements combined are sufficient to determine an exact number of meals that cost at least $25, and the correct choice is (C).

5. (C)

   Step 1: Analyze the Question

   You are provided with two pieces of information: diesel fuel is $1.25 per gallon and the truck in question refuels at a rate of 2 gallons every 5 seconds. As the choices are in seconds, minutes, and hours, you need to be comfortable converting from one unit to another.

   Step 2: State the Task

   Find the amount of time it would take to add $40 of diesel fuel to the truck.

   Step 3: Approach Strategically

   There’s a lot going on in this problem, so the key is to take things one step at a time. Begin by figuring out the amount of fuel you’re looking to add. At a price of $1.25 per gallon, the truck owner is looking to refuel his vehicle with 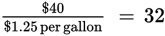gallons of fuel. Fuel enters the vehicle at 2 gallons every 5 seconds, so it would take × 5 seconds = 80 seconds to refuel the vehicle. Finally, 80 seconds is 1 minute and 20 seconds, which makes (C) the correct answer.

   Step 4: Confirm Your Answer

   When evaluating the choices for a question like this, be careful not to read them too quickly, as (E) is designed to look very similar to the correct answer at first glance.

6. (E)

   Step 1: Analyze the Question

   You’re given a rate, and it looks like you’ll have to convert it. You’ll have to pay close attention to the units (seconds, hours, minutes, etc.) so you make the right conversion.

   Step 2: State the Task

   Convert 1.02 kilometers per second into terms of kilometers per hour. In other words, you start with this:

   

   And want to end up with this:

   

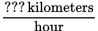
   Step 3: Approach Strategically

   You don’t want to change the “kilometers” term, but you do want to change “seconds” to “hours.” There are 60 seconds per minute and 60 minutes per hour. In other words, the rates are:

   

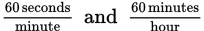
   Then set up multiplication so that the “seconds” cancel, as do the “minutes”:

   

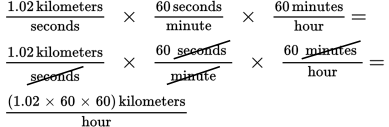
   So your calculation is 1.02 × 60 × 60. That’s 1.02 × 3,600. While this isn’t the hardest calculation in the world, you don’t have to perform it at all, as only (E) is larger than 3,600.

   Step 4: Confirm Your Answer

   Reread the question stem, making sure that you didn’t miss anything about the problem. For example, if you solved for kilometers per minute, you’d have selected (B). This step would save you from choosing the wrong answer.

7. (B)

   Step 1: Analyze the Question

   This question gives you a complicated setup, with several different variables. Picking numbers will probably be a safe approach.

   Step 2: State the Task

   Your task is to calculate the price per magnet. The word per signals a rate:

   

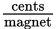
   Many GMAT word problems have wrong answers that can be eliminated logically, and this is no exception. Since the answer is the amount of money that each magnet costs, you can be sure that the more dollars charged per crate (m), the more money each magnet would cost. In other words, the right answer would have to get bigger as m gets bigger. (A), (C), and (E) all have m in the denominator, so those expressions would get smaller as m gets bigger. Those answers can be eliminated.

   Step 3: Approach Strategically

   You need to solve for “magnets” and “cents.”

   What do you know about the number of magnets? According to the question stem, “Magnabulk Corp sells boxes holding d magnets.” That means d magnets per box:

   

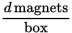
   What do you know about boxes? “Boxes are shipped in crates, each holding b boxes.” That’s b boxes per crate:

   

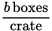
   What do you know about the crates? “Magnabulk charges m dollars for each crate.” That’s m dollars per crate:

   

   And, of course, dollars convert to cents at the rate of 100 cents per dollar:

   

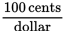
   Then set up multiplication such that cents are in the numerator, magnets in the denominator, and everything else cancels:

   

   That’s (B).

   Picking numbers will also work well. Just choose permissible and manageable numbers. Say d = 2, b = 5, and m = 4. With these numbers substituted, the question stem reads as follows:

   Magnabulk Corp sells boxes of 2 magnets. The boxes are shipped in crates, each holding 5 boxes. What is the price charged per magnet, in cents, if Magnabulk charges $4 for each crate?

   Each crate holds 10 magnets, so 400 cents for 10 magnets is 40 cents per magnet. Plugging in d = 2, b = 5, and m = 4:

   (A) 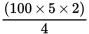= 25 × 10 = 250. Eliminate.

   (B)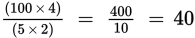. Possibly correct.

   (C)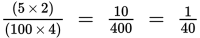. Eliminate.

   (D)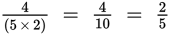. Eliminate.

   (E). Eliminate.

   Step 4: Confirm Your Answer

   Reread the question stem, making sure that you didn’t miss anything about the problem. For example, the problem uses m for dollars and d for magnets instead of vice versa.

8. (E)

   Step 1: Analyze the Question

   A motorcyclist rides from highway marker to highway marker for different distances and durations and at different speeds. With so many pieces of information given for this multi-stage journey, you should be prepared to track it all with a table.

   Step 2: State the Task

   Find the average speed, in miles per hour (mph), of the motorcyclist while driving from marker B to marker C.

   Step 3: Approach Strategically

   With so much information to keep track of, the best way to approach this problem is first to organize all of the given concrete information into a table:

   	Rate (mph)	Time (hr)	Distance (miles)
   Marker A to marker B			120
   Marker B to marker C	?
   Total	45

   You’re told that the ride from marker A to marker B took 3 times as long as the ride from marker B to marker C and that the distance from marker B to marker C is half the distance from marker A to marker B. Using t for the amount of time, in hours, that it took to ride from marker B to marker C, you can now fill in your table with the following:

   	Rate (mph)	Time (hr)	Distance (miles)
   Marker A to marker B		3t	120
   Marker B to marker C	?	t	60
   Total	45	4t	180

   It took 4t hours to go 180 miles at 45 miles per hour, so t must equal 1. You can now finish the table:

   	Rate (mph)	Time (hr)	Distance (miles)
   Marker A to marker B	40	3	120
   Marker B to marker C	60	1	60
   Total	45	4	180

   You’re looking for the average speed from marker B to marker C, which, according to the table, is 60 miles per hour. The correct choice is (E).

   Step 4: Confirm Your Answer

   When using a table to organize information, check to ensure that the given pieces of information are filled into the correct parts of the table. Also remember that unlike time and distance, for which the values in the columns sum to get the total, the only way to calculate rate is to divide the distance for that row by the corresponding time.

9. (B)

   Step 1: Analyze the Question

   A journey consists of three parts of equal distance, traveled at different speeds. You know both the speed and the time needed to cover the first section, so you can derive the distance of each section from this information. The speeds for the second and third parts of the journey are given in terms of the speed for the previous part.

   Step 2: State the Task

   Use the average rate formula to calculate the hiker's average speed for the entire journey.

   Step 3: Approach Strategically

   To find the average rate of speed for the entire journey, you'll need the total distance hiked and the total time the hike took. 

   To find the distance of the first section of the hike, use the distance formula: Distance = Rate × Time. In this case, that means distance = 3 mph × 1.5 hours = 4.5 miles. Since each section is the same length, each section of the hike is 4.5 miles, and the total hike is 3 × 4.5 miles.

   Now calculate the time needed for the second section of the hike. This will be distance divided by speed. The hiker's speed on the second section is 25% less than the speed on the first section, which is 100 − 25% = 75% of the starting speed; calculate 0.75 × 3 mph = 2.25 mph. (Be careful here! You have to apply the percentage to the hiker's rate, not his time.) Thus, the time needed for the second section of the hike is 4.5 miles ÷ 2.25 mph = 2 hours. 

   For the third section, apply the same process: the hiker's rate is twice his rate on the second section, so that's 2 × 2.25 mph = 4.5 mph. Again the distance is 4.5 miles, so the time needed is 4.5 miles ÷ 4.5 mph = 1 hour. Therefore, the time for the entire hike is 1.5 hours + 2 hours + 1 hour = 4.5 hours.

   Finally, calculate the average rate for the journey: .

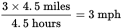   You might find it helpful to organize the information in a table and fill in each piece of information as you find it:

   	Rate (mph)	Time (hrs)	Distance (miles)
   Part 1 of hike	3	1.5	3 × 1.5 = 4.5
   Part 2 of hike			4.5
   Part 3 of hike			4.5
   Entire hike	?

   Now calculate the data for each cell:

   	Rate (mph)	Time (hrs)	Distance (miles)
   Part 1 of hike	3	1.5	3 × 1.5 = 4.5
   Part 2 of hike	0.75 × 3 = 2.25	4.5 ÷ 2.25 = 2	4.5
   Part 3 of hike	2 × 2.25 = 4.5	4.5 ÷ 4.5 = 1	4.5
   Entire hike	?		3 × 4.5

   Finally, find the time and then the rate for the entire trip:

   	Rate (mph)	Time (hrs)	Distance (miles)
   Part 1 of hike	3	1.5	3 × 1.5 = 4.5
   Part 2 of hike	0.75 × 3 = 2.25	4.5 ÷ 2.25 = 2	4.5
   Part 3 of hike	2 × 2.25 = 4.5	4.5 ÷ 4.5 = 1	4.5
   Entire hike	(3 × 4.5) ÷ 4.5 = 3	1.5 + 2 + 1 = 4.5	3 × 4.5

   The correct choice is (B).

   Step 4: Confirm Your Answer

   Be sure that you've properly applied the percent adjustments to the appropriate speeds for each section of the hike and that you used the correct formula, Average rate = Total distance ÷ Total time, to find the final answer.

10. (D)

    Step 1: Analyze the Question

    This is another multi-stage journey question. So despite the intimidating presentation, you know that you will transfer the data from the question stem into this chart:

    	Rate (mph)	Time (hr)	Distance (miles)
    Day 1	?
    Day 2
    Entire trip

    Step 2: State the Task

    Solve for speed on the first day, which is the top-left box of the chart.

    Step 3: Approach Strategically

    Before you get too worried about what your solution will be, plug the data into the chart to help organize your thinking. The first thing you read is “On the second day, he drove 3 hours longer . . . than he drove on the first day.” You know the total time will be 21 hours, so you can’t just pick a number. Use t for time on the first day. That makes time on the second day t + 3.

    Similarly, “On the second day, he drove . . . at an average speed of 15 miles per hour faster than he drove on the first day,” allows you to say that if r is speed on the first day, then r + 15 is speed on the second day. The rest of the data is simply numerical:

    	Rate (mph)	Time (hr)	Distance (miles)
    Day 1	r (?)	t
    Day 2	r + 15	t + 3
    Entire trip		21	1,020

    Since the total of the two days’ times will be the time for the entire trip, you can say:

    t + (t + 3) = 21

    2t + 3 = 21

    2t = 18

    t = 9

    Put that into the chart:

    	Rate (mph)	Time (hr)	Distance (miles)
    Day 1	r (?)	9
    Day 2	r + 15	12
    Entire trip		21	1,020

    That allows you to find distance for each day by multiplying (Rate × Time = Distance).

    	Rate (mph)	Time (hr)	Distance (miles)
    Day 1	r (?)	9	9r
    Day 2	r + 15	12	12(r + 15)
    Entire trip		21	1,020

    Now you have an equation that will allow you to solve for r, which is what you’re looking for—speed on Day 1. Since the total of the 2 days’ distances will be the distance for the entire trip, you can say:

    9r + 12(r + 15) = 1,020

    9r + 12r + 180 = 1,020

    21r = 840

    r = 40

    The answer is (D).

    Step 4: Confirm Your Answer

    Reread the question stem, making sure that you didn’t miss anything about the problem. For example, if you inverted some information about the 2 days, you could end up with (A).

11. (C)

    Step 1: Analyze the Question Stem

    This is a Yes/No question. The stem asks you to compare the time it took two people to complete the same journey of 40 km. Remember that . Since you’re given the distance in the question stem, you'll need information adequate to determine both travelers’ rates of speed.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) gives you Jon’s speed. Together with the question stem, this is enough information to determine the time required by Jon to complete the journey. But you  get no information about Ann. Statement (1) is insufficient. You can eliminate (A) and (D).

    Statement (2) and the question stem together give enough information to determine the time Ann took to complete the journey but nothing about Jon. Statement (2) is also insufficient. Eliminate (B).

    Combining the two statements, you have enough to determine both the time Jon took to complete the journey and the time Ann took to complete the journey. Note that you don’t need to calculate their times; knowing that you could calculate them is enough. (C) is correct.

12. (A)

    Step 1: Analyze the Question

    Pump A takes 3 hours to empty a tank, and Pump B takes 4 hours to empty half of the same tank—that is, it would take Pump B 8 hours to empty the whole tank.

    Step 2: State the Task

    Use an understanding of combined rates to find the number of hours it would take both pumps, working together at their respective rates, to empty half the tank.

    Step 3: Approach Strategically

    While you could calculate this problem using the combined work formula, some critical thinking can go far here. Since Pump A by itself can empty the tank in 3 hours, it stands to reason that Pump A and Pump B working together must be able to empty the tank in fewer than 3 hours. Notice that (C), (D), and (E) are all greater than 3, so eliminate all of them. Furthermore, you're trying to find how long it would take the two pumps to empty only half of the tank, so logically, that must be less than half of 3 hours, or 1.5 hours. Since (B) is greater than 1.5, you can eliminate it as well. Thus, the correct answer is the only remaining choice, (A).

    Step 4: Confirm Your Answer

    If you used the logical approach above, then to confirm your answer, use the combined work formula, . (If you used the formula in the first place, then check your answer against the logic of the situation.) 

    In this case, T is the time Pump A and Pump B take to empty the entire tank when working together, and A and B are the respective amounts of time that it takes each pump to empty the tank individually. Plug the given times into this formula and solve:

    T =

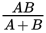
    T =

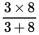
    T =

    So it takes Pump A and Pump B working together 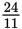 hours to empty the whole tank. Since you need to find how long it would take to empty just half the tank, that's  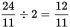hours.

13. (C)

    Step 1: Analyze the Question

    This is a combined work problem with a twist. Rather than being given the time each machine can complete the job separately, you're given the time it takes the two machines together to complete the job and the portion of the job one of the two machines can do in the same amount of time.

    Step 2: State the Task

    Find how long it will take the second machine, working alone, to complete the entire job.

    Step 3: Approach Strategically

    You can use the combined work formula, . In this formula, A and B are the times that each machine can do the job in time T. You're given that Machine 1 and Machine 2 together can produce 12,000 meters of cable in 1 hour, so in this scenario, T = 1. 

    You're also given that Machine 1 by itself can produce 5,000 meters of cable in 1 hour. From this, you can find how long it would take Machine 1 to complete the entire 12,000 meters: Machine 1 can complete 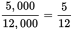 of the job in 1 hour. Therefore, Machine 1 will take 1 hour ÷  hours/job =  hours to complete the entire job. 

    Now plug this information into the combined work formula: . Multiply both sides by the denominator to simplify: 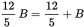. Multiply each term by 5 to clear the fractions: 12B = 12 + 5B. Then 7B = 12, and 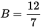. This is the time it would take Machine 2 to make 12,000 meters of cable, and (C) is correct.

    Step 4: Confirm Your Answer

    You can confirm your answer with an alternative approach. Once you've determined that Machine 1 can do  of the job (producing 12,000 meters of cable) in 1 hour, you can deduce that Machine 2 must be able to complete 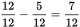 of the job in 1 hour. Set up a proportion of jobs to hours and solve for the hours for 1 job:

    

    Cross multiply: 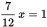, and . 

14. (A)

    Step 1: Analyze the Question

    Because two trucks are traveling the same route and the slower truck sets out on the journey before the faster truck, this is an overtaking problem. The relative speed of the two trucks is the difference between their speeds; this is the rate at which the faster truck catches up with the slower truck. There are limiting factors included in the question, including the speed limits on the roads and the maximum speeds of the trucks. 

    • For the first 30 miles, Truck F travels at 60 mph and Truck S at 50 mph, so F is gaining on S at the rate of 10 mph.
    • Both trucks travel the next 10 miles at 40 mph.
    • For the final 60 miles, Truck F travels at 55 mph and Truck S at 50 mph, so F is traveling 5 mph faster than S.

    Step 2: State the Task

    Determine the distance from Betaville to the point where Truck F overtakes Truck S.

    Step 3: Approach Strategically

    Since there are different speeds involved in the three segments of the journey, analyze this piece by piece. The first leg is 30 miles. Using the formula Distance = Rate × Time rearranged as 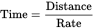, Truck S traverses this leg in 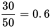  hours. Truck F starts 12 minutes later, or  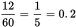hours later. It completes this leg in hours, which is 0.1 hours less than the time for S. However, since Truck F started 0.2 hours after Truck S, Truck F arrives at the end of the 30-mile leg 0.2 − 0.1 = 0.1 hour after Truck S.

    The trucks will complete the 10-mile segment in the same amount of time since they both are limited to 40 mph, so Truck F will begin the final 60-mile leg 0.1 hour after Truck S does. 

    For the last 60 miles, Truck F overtakes Truck S at a rate of 5 mph. Truck S starts this leg 0.1 hour before Truck F. Traveling at 50 mph, that is a 50 × 0.1 = 5-mile head start. So, given that F is traveling 5 mph faster, it would catch up with S in exactly an hour. The point at which this occurs would be 1 hour × 55 mph = 55 miles from the start of the leg. Because the entire segment is 60 miles long, this point is 60 − 55 = 5 miles from Betaville. (A) is correct.

    Step 4: Confirm Your Answer

    The tricky part of this question is all the details presented regarding distances and speeds. Reread the question stem, making sure that you used the correct values, and check your calculations. (B) is the distance the trucks traveled on the last leg before F catches up to S. (D) is the correct distance from Alphaburg rather than from Betaville.

15. (A)

    Step 1: Analyze the Question

    A $1,000 certificate of deposit paid 4% annual interest compounded quarterly until it matured in 4 years, which means that 1% was added to the principal 4 times per year. Thereafter, the certificate paid 2% annual simple interest on the compounded amount. Binh purchased such a certificate and redeemed it after 6 years.

    Step 2: State the Task

    Determine which expression among the answer choices represents the value of the CD after 6 years.

    Step 3: Approach Strategically

    The formula for compound interest is Principal × (1 + r)^t, where r is the interest rate per time period expressed as a decimal and t is the number of time periods. Since this CD had a 4% annual rate with interest compounded quarterly, 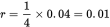 . Because the compounding occurred 4 times per year for 4 years, t = 4 × 4 = 16. Thus, the value of the CD at the end of 4 years was 1,000 × (1.01)¹⁶. This amount then amassed simple interest. The formula for simple interest is Principal × (1 + rt). In this case, the interest rate was 2%, so r = 0.2, and it accrued for 2 years, so t = 2. So Principal × (1 + 0.02(2)) = Principal × 1.04. Thus, the total value after 6 years was (1.01)¹⁶ × 1.04. (A) is correct.

    Step 4: Confirm Your Answer

    Whenever an interest problem involves compounding other than annually, be certain to adjust the interest rate per compounding period and the number of times that compounding occurs. Double-check these values in your solution.

16. (B)

    Step 1: Analyze the Question

    You’re given a piece of information other than just interest rate and principal. How might it influence your solution? You may not be sure yet, but it’s unlikely to be extraneous information. Also, the word approximate should make you happy: you may be able to estimate rather than calculate.

    Step 2: State the Task

    What is the approximate value in 42 years of a $40,000 investment that earns 5% compound annual interest?

    Step 3: Approach Strategically

    This problem is a great example of why strategic reading and logical analysis should precede any math. If you rush blindly into math, you’d get Total = $40,000 × (1.05)⁴². There’s no way to solve, even approximately, without a calculator.

    But what if you approached the problem strategically? You’re asked for “total value of the investment.” Scan through the question stem looking for information related to total value, and you find “the amount of an investment will double in approximately 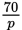years, where p is the percent interest.”

    Then search for the interest and discover that it is 5%. So you now know that the investment will double every years—or every 14 years.

    Now look for how many years the money is invested and see that it’s 42 years: 42 is 14 × 3, so 42 years means 3 doublings. The total value will be approximately $40,000 × 2 × 2 × 2 = $40,000 × 8 = $320,000.

    The answer is (B).

    Step 4: Confirm Your Answer

    Reread the question stem, making sure that you didn’t accidentally skip over any important aspects of the situation.

17. (E)

    Step 1: Analyze the Question

    The question addresses compound interest. It’s worth noting that the interest is not annual interest but is compounded every 3 months. Since there are 12 months per year, the interest compounds 4 times per year.

    Although there are variables in the answer choices, picking numbers probably won’t be needed, as the answers are just various ways that the interest formula might be constructed.

    Step 2: State the Task

    Solve for the original amount in the account. Call it P for principal.

    Step 3: Approach Strategically

    Since the question seems all about whether you can properly construct the compound interest formula, make sure that you carefully set up each part. The general formula is this:

    T = P(1 + r)^t

    All of the answer choices use 1.015, so you know for certain—if you didn’t already—that inside the parentheses must be 1.015:

    T = P (1.015)^t

    Since interest is compounded 4 times per year for 5 years, t = 4 × 5 = 20.

    T = P (1.015)²⁰

    = P

    The answer is (E).

    Step 4: Confirm Your Answer

    Reread the question stem, making sure that you didn’t accidentally skip over any important aspects of the situation. For example, if you initially missed the “every 3 months” part of the stimulus, you would have been looking for an answer with an exponent of 4. This step gives you the chance to catch such errors.

18. (B)

    Step 1: Analyze the Question

    This question provides you with information about a group of 65 books; every book is classified as either fiction or nonfiction and as either greater than 200 pages or less than or equal to 200 pages (to avoid having these irrelevant numbers in your head, you might paraphrase this as "long books and short books"). Plan on organizing the details in a table to keep track of them.

    Step 2: State the Task

    Find the total number of nonfiction books "of no more than 200 pages"—in other words, less than or equal to 200 pages, or short nonfiction books.

    Step 3: Approach Strategically

    Organize all of the given information into a table:

    	Fiction	Nonfiction	Total
    Short		?	25
    Long	20
    Total	35		65

    With everything organized, fill in the blanks. Once you have two entries in a row or column, you can fill in the third entry for that row or column. If the two known values are subtotals, add them to get the total; if one of the known values is a total, subtract the known subtotal from the total to get the other subtotal. 

    	Fiction	Nonfiction	Total
    Short	15	10	25
    Long	20	20	40
    Total	35	30	65

    Arrive at the correct answer either by subtracting 15 short fiction books from 25 total short books in the first row or by subtracting 20 long nonfiction books from 30 total nonfiction books in the second column. The number of short nonfiction books is 10. (B) is correct.

    Step 4: Confirm Your Answer

    When using a table, check to make sure that you answer with the right piece of information; three of the incorrect choices are numbers that fill in other cells in the table. Also, double-check that you answered the right question; for example, if you read the question as "How many nonfiction books of more than 200 pages" instead of "no more than 200 pages," you may have chosen (C).

19. (C)

    Step 1: Analyze the Question

    Since students are split into two potentially overlapping sets—those who study Spanish and those who study French—this is an overlapping sets problem. To help organize the data, draw a table:

    	French	Not French	Total
    Spanish		?
    Not Spanish
    Total

    Step 2: State the Task

    You need to find a valid range, with both an upper and lower limit, for those who are in the “Spanish and not French” category.

    Step 3: Approach Strategically

    You have a piece of data with a lower limit (“at least 90”) but nothing with an upper limit. It’s hard to know intuitively what that upper limit should be, so put in the data from the question stem so you can understand the problem more clearly:

    	French	Not French	Total
    Spanish		?	170
    Not Spanish		at least 90
    Total	110		300

    From this, you can figure out how many do not study each language:

    	French	Not French	Total
    Spanish		?	170
    Not Spanish		at least 90	130
    Total	110	190	300

    Now that you have a clearer understanding of the situation, you can understand more about the limitations on the “at least 90” group. Since the total of the “not Spanish” row is 130, there could be no more than 130 in the “not Spanish and not French” category. (More than 130 would require a negative number of students in the “French and not Spanish” category.)

    	French	Not French	Total
    Spanish		?	170
    Not Spanish		90 to 130	130
    Total	110	190	300

    The “Spanish and not French” category must add with “90 to 130” to yield 190. There could be as many as 100 (since 100 + 90 = 190) or as few as 60 (since 60 + 130 = 190).

    The answer is (C).

    Step 4: Confirm Your Answer

    Reread the question stem, making sure that you didn’t accidentally misread anything. For example, (E) is the value of the “Spanish and French” category.

20. (A)

    Step 1: Analyze the Question Stem

    This is a Value question. It is asking for the number of reporters who cover all three continents.

    There’s a lot of information, and it begs to be simplified. As the reporters may cover one, two, or three of the continents, this is an overlapping sets question. But with three sets, a chart-based approach would be too unwieldy. The best way to visualize three overlapping sets is with a Venn diagram. Take care to put the totals for each continent just outside the circles so that you don’t lose the distinction between the number covering a continent and the number covering only that continent.

    So that you know what you need, put an x in the “all three continents” space on the diagram.

    

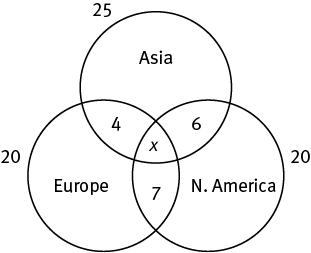
    You can continue to analyze your information. A total of 25 reporters cover Asia, 6 of whom also cover only North America, 4 of whom also cover only Europe, and x of whom also cover both Europe and North America.

    Therefore, 25 − (6 + 4 + x), or 15 − x, cover only Asia.

    Similarly, 20 − (4 + 7 + x), or 9 − x, cover only Europe, and 20 − (7 + 6 + x), or 7 − x, cover only North America.

    Put that into your diagram:

    

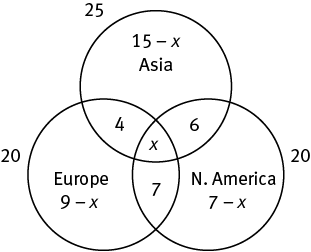
    Many kinds of information, therefore, would allow you to figure out the number of reporters who cover all three continents. Any data that lets you make an equation with x would be sufficient.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) says that the grand total of all the reporters is 38. In other words, if you added up all the various subcategories, you’d get 38. That’s sufficient, as the only variable in that equation would be x. Eliminate (B), (C), and (E).

    Although you wouldn’t want to set the whole thing up (you’d stop as soon as you knew that you could set up the equation), here’s what it would be:

    (15 − x) + (9 − x) + (7 − x) + 4 + 7 + 6 + x = 38

    Once the information from the question stem has been fully simplified and analyzed, you see that Statement (2) is only saying that (15 − x) > (7 − x). That’s just 15 > 7, which is hardly new information. Statement (2) adds nothing and must be insufficient. (A) is correct.