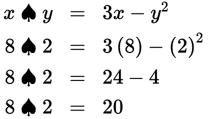
The GMAT uses classic function notation that you may recall from your later high school algebra classes. It also uses some untraditional notation, such as ⋄, ♠, or ⊗. Both types boil down to substitution.
The basic idea is that these questions ask you to substitute values or operations in a unique way described by the problem. Here’s a classic function problem.
Example: What is the minimum value of the function f(x) = x2 − 1?
What this problem is telling you is that whatever number is between those parentheses gets substituted in place of x in x2 − 1. For instance, f(2) = 22 − 1 = 3.
A strategic way to solve would be to substitute whatever answer choices the GMAT gives you as the answer to the function. Some may not be possible; some will be. For example, x2 = −4 isn’t possible, since the GMAT uses only “real” numbers, and the square of a real number must be non-negative. The smallest of the possible answer choices would be the correct response.
You could solve this question logically, too. The value of the function will be smallest when x2 is smallest. Squaring a negative number produces a positive number, so x2 can never be negative. The smallest result you could get is x2 = 0. So the smallest x2 − 1 can be is 0 − 1, or −1.
Some questions offer strange symbols but work basically the same way—as rules for how to substitute.
Example: If x ♠ y = 3x − y2, then what is the value of 8 ♠ 2?
The given equation is really just a rule for substitution. Whatever is to the left of the ♠ symbol is x and should be substituted in place of x in 3x − y2. Similarly, anything to the right of ♠ is y and should be substituted for y.
For the most part, symbols on the GMAT define operations (i.e., the process that one or more numbers must be put through). Occasionally, the GMAT will use symbols to stand in for digits, but this isn’t as common.
Now let’s use the Kaplan Method on a Data Sufficiency question dealing with functions and symbolism:
You need to determine whether there is sufficient information to find the value of 6 ♣ 2, and you are told that the symbol ♣ can stand for any one of the four operations of addition, subtraction, multiplication, or division.
Now, since there is no further information in the question stem, look at the statements.
Statement (1) tells you that 0 ♣ 3 = 0. The potential operations that yield this value are:
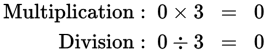
So ♣ could stand for multiplication or division. However, 6 × 2 = 12 and 6 ÷ 2 = 3, so there is more than one possible answer to the question. Statement (1) is insufficient. Eliminate (A) and (D).
Statement (2) tells you that 2 ♣ 1 = 2. The potential operations that yield this value are:
So again, ♣ could be multiplication or division; as you saw in evaluating the first statement, the value of 6 ♣ 2 changes depending on whether the symbol represents multiplication or division. More than one answer is possible for the question, so Statement (2) is insufficient. Eliminate (B).
Taking the statements together, you still know only that ♣ could be multiplication or division. However, since each of these operations yields a different value, the two statements taken together are insufficient. Therefore, (E) is correct.
and 
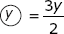, for all integers x and y. If m = 2, 
is equal to which of the following?
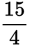
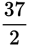
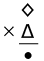
. If x ♦ 5 = 2, then x =