Absolute Value

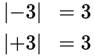
The absolute value of a number is the number’s distance from zero on the number line. It is denoted by two vertical lines. Since absolute value is a distance, it is always non-negative. For instance, both +3 and −3 are 3 units from zero, so their absolute values are both 3.

Example:

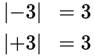
The GMAT will increase the difficulty of an absolute value question (and therefore the benefit of getting it right) by using variables.

Example: |z| = 3

You don’t know what z equals. Since z is 3 units from 0, you can deduce that it either equals +3 or −3.

So you can rewrite this one equation as two:

z = 3 OR z = −3

Another way to conceptualize this is as follows:

|z| = 3

±z = 3

+z = 3 OR –z = 3

z = 3 OR z = −3

These problems are fairly straightforward when only one number is involved. But what about expressions? Treat the absolute value bars as parentheses and figure out the value of what’s inside before you perform the operation. Needless to say, the GMAT will base wrong answers on performing these operations in the wrong order.

INCORRECT: |–3| + |5| = |–3 + 5| = |2| = 2

CORRECT: |–3| + |5| = 3 + 5 = 8

Now, let’s look at what happens when you are given expressions with variables.

Example: |x – 3| = 3

Believe it or not, this isn’t any different from the earlier example:

|z| = 3

z = 3 OR z = −3

Think of it this way:

|<<chunk>>| = 3

<<chunk>> = 3 OR <<chunk>> = −3

Since the <<chunk>> here is x – 3, that gives you the following:

|x – 3| = 3

x – 3 = 3 OR x – 3 = −3

x = 6 OR x = 0

The GMAT sometimes adds another layer of complexity to absolute value questions by including inequalities. The key is to remember that when considering the possible negative value, the inequality sign changes direction:

|x – z| > 3

x – z > 3 OR x – z < −3

Don’t worry if that concept seems a little strange to you right now. We’ll explore this idea further when we discuss inequalities later in this chapter.

In-Format Question: Absolute Value on the GMAT

Now let’s use the Kaplan Method on a Problem Solving question dealing with absolute value:

1. How many possible integer values are there for x, if |4x – 3| < 6?
   1. One
   2. Two
   3. Three
   4. Four
   5. Five

Step 1: Analyze the Question

You’re asked for the number of integers that could satisfy an inequality. The inequality includes an expression with an absolute value.

Step 2: State the Task

You’ll have to evaluate the inequality, find the range of x on the number line, and then count the number of integers that could be acceptable values of x. Remember that the correct answer is not any particular value of x but the number of possible integer values.

Step 3: Approach Strategically

Since you have an absolute value in an expression, you have to consider two possibilities: either 4x – 3 < 6 or –(4x – 3) < 6. Multiply both sides of the second inequality by −1, remembering to reverse the inequality sign: the second inequality can be written as 4x – 3 > −6. Combine these two statements to analyze the expression more quickly: −6 < 4x – 3 < 6. Adding 3 to each of the three members, you have −3 < 4x < 9. Dividing each of the three members by 4 gives you . The possible integer values of x such that are 0, 1, and 2. There are three such values, and (C) is correct.

Step 4: Confirm Your Answer

Confirm that your calculations are correct. Quickly sketch the range of x on a number line to confirm your count of the number of possible integer values of x.

Takeaways: Absolute Value

• Use these three tools to solve absolute value problems:
  1. Interpret absolute value as the expression’s distance from zero on the number line.
  2. Draw a number line.
  3. Write two equations for every equation with an absolute value; one or the other of these new equations must be true.
• When there is an absolute value sign, there is a high likelihood of a trap answer for those who assume the quantity inside can only be positive.

Practice Set: Absolute Value on the GMAT

10. Which of the following could be the value of x, if |4x – 2| = 10?
    1. –3
    2. –2
    3. 1
    4. 2
    5. 4
11. What is the value of p?
    1. –|p| = −2
    2. p² – 4 = 0
12. If , then which of the following must be true?
    1. m > 5
    2. m < 5
    3. m = 5
    4. m ≠ 5
    5. m < −5