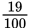
In the Problem Solving chapter of this book, you learned how to use the picking numbers strategy to deal with questions that involve taking percents of unspecified values. Questions that specify the exact values are often more straightforward, but they require your familiarity with several formulas for dealing with fractions and percents.
Key to these questions is the fact that percent is just another word for “per one hundred.”
Therefore, 19% (or 19 percent) means 19 hundredths
or
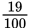
or 0.19
or 19 out of every 100 things
or 19 parts out of a whole of 100 parts.
GMAT questions will often require that you convert among percents, decimals, fractions, and ratios. Below you will learn the process for making each of these conversions, but they all boil down to using the percent formula:
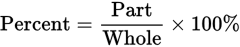
Plug in the information you have and solve for the missing pieces.
To make a percent from a decimal or fraction, multiply by 100%. Since 100% means 100 hundredths, or 1, multiplying by 100% will not change the number.
Example: 0.17 = 0.17 × 100% = 17%
Example: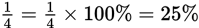
To drop a percent, divide by 100%. Once again, dividing by 100%, which is equivalent to 1, will not change the number.
Example: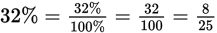
Example:
To change a percent to a decimal, just drop the percent sign and move the decimal point two places to the left. (This is the same as dividing by 100%.)
Example: 0.8% = 0.008
Being familiar with the following fraction-to-percent equivalents can save you a lot of time on questions that require you to perform such conversions.
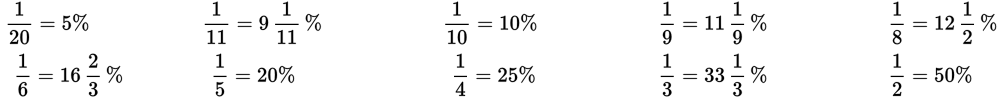
Percent problems will usually give you two of the terms from the formula below and ask for the third. It is usually easiest to change the percent to a common fraction before performing the calculation. Most percent problems can be solved by plugging into a variant of the percent formula:
Percent × Whole = Part
In percent problems, the whole generally will be associated with the word of, and the part will be associated with the word is. The percent can be represented as the ratio of the part to the whole, or the is to the of.
Example: What is 25% of 36?
Here you are given the percent and the whole. To find the part, change the percent to a fraction, then multiply. Use the following formula:
Since 25% =
, you are really being asked what one-fourth of 36 is.
Example: 13 is
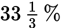of what number?
Recall that
Example: 18 is what percent of 3?
Other problems will ask you to calculate “percent greater than” or “percent less than.” In these cases, it is the number that follows the word than to which the percentage is applied.
You may find it faster to convert percent greater/less than to percent of. “x% greater than” becomes “(100 + x)% of.” “ x % less than” becomes “(100 − x)% of.”
Example: What number is 15% less than 60?
Example: What is the price of a television that costs 28% more than a $50 radio?
Let t equal the price of the television and r equal the price of the radio.
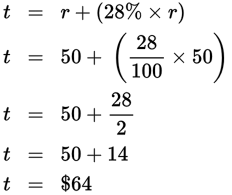
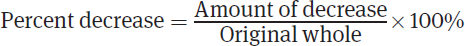
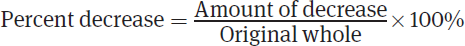
New whole = Original whole ± Amount of change
When dealing with percent increase and percent decrease, always be careful to put the amount of increase or decrease over the original whole, not over the new whole.
Example: If a dress is offered for a discounted price of $120, what is the percent discount if the regular price is $150?
You’re asked to calculate the discount, so you’ll use the regular selling price of $150 as the original whole. The difference in prices is $150 − $120, or $30.
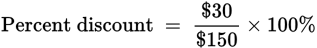
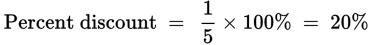
Combining Percents: On some problems, you’ll need to find more than one percent, or a percent of a percent. Be careful: you can’t just add percents, unless the percents are of the same whole. Let’s look at an example.
Example: The price of an antique is reduced by 20 percent, and then this discount price is further reduced by 10 percent. If the antique originally cost $200, what is its final price?
First, you know that the price is reduced by 20%. That’s the same thing as saying
that the price becomes (100% − 20%), or 80% of what it originally was. Eighty percent
of $200 is equal to
or $160. Then, this price is reduced by 10%. So 10% × $160 = $16, and the final price of the antique is $160
− $16 = $144.
A common error in this kind of problem is to assume that the final price is simply a 30 percent reduction of the original price. That would mean that the final price is 70 percent of the original, or 70% × $200 = $140. But, as you’ve just seen, this is not correct. Adding or subtracting percents directly only works if those percents are being taken of the same whole. In this example, since you took 20% of the original price, and then 10% of the reduced price, you can’t just add the percents together.
Note that in this example, a 20% reduction followed by a 10% reduction does not equal a 30% reduction but rather one of 28%. This will always happen—two decreases cause a total percent decrease of less than the sum of the two individual percents. This is because the second percent decrease is taken from a smaller starting value. Likewise, two increases cause a total increase of more than the sum of the two individually, since the second percent increase is calculated based on a higher starting point. You can use this fact to estimate an answer quickly.
Now let’s use the Kaplan Method on a Problem Solving question that involves percents with specified values:
This question is asking for the lowest possible price of pet food that has been marked down twice. Another way to phrase the question is that you want the maximum possible discount. So you’ll take the maximum discount at each stage of the markdown to determine the lowest price.
Since the question gives you an actual starting value for the price, you cannot pick numbers to make the calculations easier. Notice that you could backsolve this question, since the answer choices are all numbers, but since this question involves multiple discounts, backsolving could result in lots of calculation. The more efficient approach here is to use what you know about percent decrease.
Using the starting value of $20, you must apply the two maximum discounts, one after the other.
The original price for the pet food was $20, and the maximum reduction the store gives is 30%. You can approach the reduction calculation in two ways:
1. You could determine 30% of $20 and then subtract this amount from $20:
$20 × 0.3 = $6; $20 − $6 = $14
2. You can find the new price directly. Since 100% − 30% = 70%, the new price is 70% of $20:
$20 × 0.7 = $14
Regardless of the approach, you find that the first reduced price is $14.
Now, you need to take the 20% discount off this reduced price. Again, you could apply either approach to calculate this value, but the second approach is more efficient: $14 × 0.8 = $11.20. (B) is correct.
Since there wasn’t much arithmetic, you can quickly check for any careless errors. Also, reread the question stem to make sure that you didn’t misinterpret anything and that you solved for the correct value.
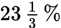
Survey of Student Preferences
