Rates and Speed—Multi-part Journeys

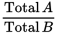
The GMAT often uses scenarios involving multi-part journeys in order to ask questions about “average rates.” In such cases, the test makers will give you information that includes two or more different rates or speeds. So far in this chapter, you’ve learned about both averages and rates, so it’s understandably tempting in this situation simply to average the different individual rates you’re given.

Don’t fall for this trap. Just as you cannot use the averages of two different portions of a group to determine the group’s overall average (unless you know the weights of the portions), you also cannot find the average speed of a journey from the speeds of two parts unless you know the proportion of time spent or distance traveled in those parts. The GMAT’s biggest trap with multi-part journeys or tasks is to offer an answer choice that fails to account for the weighting of the averages and simply splits the difference between the two portions. The GMAT writes its problems so that this is never the correct solution. Instead, you’ll need to use the average rate formula.

Average Rate (Average A per B):

Average A per B =

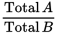
Example: John travels 30 miles in 2 hours and then 60 miles in 3 hours. What is his average speed in miles per hour?

Average miles per hour =

Notice how you can check your work on this question by applying some Critical Thinking: John’s first rate was 15 miles per hour, and his second rate was 20 miles per hour, so his average rate will fall somewhere between 15 and 20 miles per hour. You can estimate effectively on this question, as on most average rate questions, by identifying the rate at which John spent longer traveling. In this case, John spent more time traveling at 20 miles per hour, so his average rate should be closer to 20 than to 15. Indeed, 18 miles per hour is consistent with the direction in which the average rate should be weighted.

Average rate problems on the GMAT can become quite complex. If your paraphrase of the question stem is anything like “First this person moves at one speed, then at another,” then you’re dealing with a multi-part journey problem. There is frequently a lot of information to deal with.

To organize the data on complicated multi-part journey problems, try jotting down this chart on your noteboard:

	Rate	Time	Distance
Part 1 of trip
Part 2 of trip
Entire trip

This chart folds many equations into one:

• Rate × Time = Distance; each row of boxes multiplies across.
• Time (part 1) + Time (part 2) = Time (entire trip); time boxes add down.
• Distance (part 1) + Distance (part 2) = Distance (entire trip); distance boxes add down.
• Rates do not add down; they are calculated by dividing distance by time. If you need to calculate the speed for the entire trip, use the average speed formula:

Average speed =

Let’s go through a sample question, and you’ll see how the chart helps you.

A powerboat crosses a lake at 18 miles per hour and returns at 12 miles per hour. If the time taken turning the boat around was negligible and it returns by the same route, then what was the boat’s average speed for the round trip, in miles per hour?

When you notice that you have a multi-part journey problem, jot down the chart, using a question mark to indicate the value that the question asks you for:

	Rate (mph)	Time (hr)	Distance (miles)
Part 1 of trip
Part 2 of trip
Entire trip	?

Now fill in the data given by the problem:

	Rate (mph)	Time (hr)	Distance (miles)
Part 1 of trip	18
Part 2 of trip	12
Entire trip	?

Now you clearly have to get some information about either the time or the distance to be able to solve for much of anything. The only other piece of information you have is that the boat traveled the same route both times. That means the distance must have been the same. You could use the variable D, but the math will get fairly complicated if you do. Instead, keep it simple and pick numbers. A number that’s a multiple both of 18 and of 12 will make the math work out nicely, so let’s say the lake was 36 miles across:

	Rate (mph)	Time (hr)	Distance (miles)
Part 1 of trip	18		36
Part 2 of trip	12		36
Entire trip	?

Now you can solve for the times and the total distance:

	Rate (mph)	Time (hr)	Distance (miles)
Part 1 of trip	18	2	36
Part 2 of trip	12	3	36
Entire trip	?		72

And finally for total time:

	Rate (mph)	Time (hr)	Distance (miles)
Part 1 of trip	18	2	36
Part 2 of trip	12	3	36
Entire trip	?	5	72

Now you have what you need to solve for average rate. It’s mph. This answer makes logical sense, since the two rates are 18 and 12 miles per hour and the boat spent more time traveling at the lower speed, so the average is closer to 12 than to 18.

In-Format Question: Rates and Speed—Multi-part Journeys on the GMAT

Now let’s use the Kaplan Method on a Data Sufficiency question dealing with a multi-part journey:

1. What was the average speed of a runner in a race from Point X to Point Z?
   1. The runner’s average speed from Point X to Point Y was 10 miles per hour.
   2. The runner’s average speed from Point Y to Point Z was 8 miles per hour.

Step 1: Analyze the Question Stem

This is a Value question, so you need one exact speed for the trip from Point X to Point Z.

Use Critical Thinking: there’s no direct simplification to be done, but since you can sometimes calculate exact speeds with unknown distance or time, there might be a way to solve for speed without knowing the exact distance and time.

To answer the question, you’ll need either the exact distance and time or some information about distance or time that allows you to calculate speed.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) gives you some data about the trip from X to Y but nothing about X to Z. Insufficient. Eliminate (A) and (D). Likewise, Statement (2) gives you data about the trip from Y to Z but nothing about X to Z. Insufficient. Eliminate (B).

Now you must combine. Notice that something crucial is missing—information relating either the times or the distances of the X-to-Y and the Y-to-Z leg. If the X-to-Y distance were 10 miles and the Y-to-Z distance were 10 inches, the average speed would be essentially 10 mph. And if it’s the other way around, with the X-to-Y distance 10 inches and the Y-to-Z distance 10 miles, the average speed would be essentially 8 mph. The combined statements are insufficient, so the answer is (E).

Takeaways: Rates And Speed—Multi-Part Journeys

• In average rate and average speed questions, one wrong answer choice involves not accounting for the weighting of the averages. To avoid this wrong answer, use the average rate and average speed formulas.
• .
• For multi-part journeys, use a chart to organize data.
• In an average speed question, if you recognize the direction in which the speed should be weighted, you can rapidly eliminate incorrect answers.

Practice Set: Rates and Speed—Multi-part Journeys on the GMAT

8. A motorcyclist started riding at highway marker A, drove 120 miles to highway marker B, and then, without pausing, continued to highway marker C, where she stopped. The average speed of the motorcyclist, over the course of the entire trip, was 45 miles per hour. If the ride from marker A to marker B lasted 3 times as many hours as the rest of the ride, and the distance from marker B to marker C was half of the distance from marker A to marker B, what was the average speed, in miles per hour, of the motorcyclist while driving from marker B to marker C?
   1. 40
   2. 45
   3. 50
   4. 55
   5. 60
9. A hiker walks three sections of a trail that are of equal length. The first section of the trail is flat, and on this section the hiker travels at 3 miles per hour for 1.5 hours. The second section is uphill, and on this section the hiker's pace slows by 25 percent. The third section is downhill, and here his speed doubles. What was the hiker's average speed for the entire three-section hike?
   1. 1.5
   2. 3
   3. 3.25
   4. 4.5
      
   5. 9.75
10. A truck driver drove for 2 days. On the second day, he drove 3 hours longer and at an average speed of 15 miles per hour faster than he drove on the first day. If he drove a total of 1,020 miles and spent 21 hours driving during the 2 days, what was his average speed on the first day, in miles per hour?
    1. 25
    2. 30
    3. 35
    4. 40
    5. 45
11. Did Jon complete a journey of 40 kilometers in less time than it took Ann to complete the same journey?
    1. Jon traveled at an average speed of 30 kilometers per hour for the first 10 kilometers and then at an average speed of 15 kilometers per hour for the rest of the journey.
    2. Ann traveled at an average speed of 20 kilometers per hour for the entire journey.