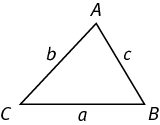
A triangle is a closed figure with three angles and three straight sides.
The sum of the interior angles of any triangle is 180 degrees.
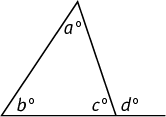
Each interior angle is supplementary to an adjacent exterior angle. The degree measure of an exterior angle is equal to the sum of the measures of the two nonadjacent (remote) interior angles.
In the figure below, a, b, and c are interior angles. Therefore a + b + c = 180. In addition, d is supplementary to c; therefore d + c = 180. So d + c =a + b + c, and d =a + b. Thus, the exterior angle d is equal to the sum of the two remote interior angles a and b.
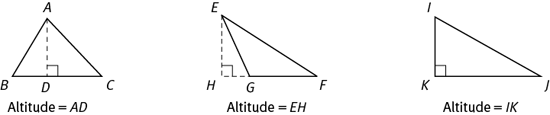
The altitude (or height) of a triangle is the perpendicular distance from a vertex to the side opposite the vertex. The altitude can fall inside the triangle, outside the triangle, or on one of the sides.
The length of any side of a triangle is less than the sum of the lengths of the other two sides, and it is greater than the positive difference of the lengths of the other two sides.
b + c > a > |b –c|
a + b > c > |a –b|
a + c > b > |a –c|
If the lengths of two sides of a triangle are unequal, the greater angle lies opposite the longer side and vice versa. In the figure above, if ∠A > ∠B > ∠C, then a > b > c.
The formula for the area of a triangle is
Example:
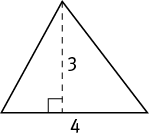
In the diagram above, the base has length 4 and the altitude length 3, so you can write
Remember that the height (or altitude) is perpendicular to the base. Therefore, when two sides of a triangle are perpendicular to each other, the area is easy to find. In a right triangle, the two sides that form the 90° angle are called the legs. Then the area is one-half the product of the legs, or
Example:
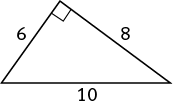
In the triangle above, you could treat the hypotenuse as the base, since that is the way the figure is drawn. If you did this, you would need to know the distance from the hypotenuse to the opposite vertex to determine the area of the triangle. A more straightforward method is to notice that this is a right triangle with legs of lengths 6 and 8, which allows you to use the alternative formula for area:
The perimeter of a triangle is the distance around the triangle. In other words, the perimeter is equal to the sum of the lengths of the sides.
Example:
In the triangle above, the sides are of length 5, 6, and 8. Therefore, the perimeter is 5 + 6 + 8, or 19.
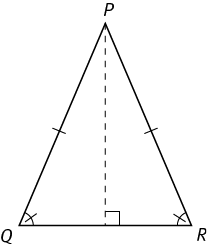
An isosceles triangle is a triangle that has two sides of equal length. The two equal sides are called legs, and the third side is called the base.
Since the two legs have the same length, the two angles opposite the legs must have the same measure. In the figure below, PQ = PR, and ∠Q = ∠R.
An equilateral triangle has three sides of equal length and three 60° angles.
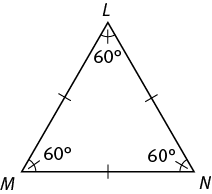
Triangles are similar if corresponding angles have the same measure. For instance, any two triangles whose angles measure 30°, 60°, and 90° are similar. In similar triangles, corresponding side lengths are proportional to one another. Triangles are congruent if corresponding angles have the same measure and corresponding sides have the same length.
Example:
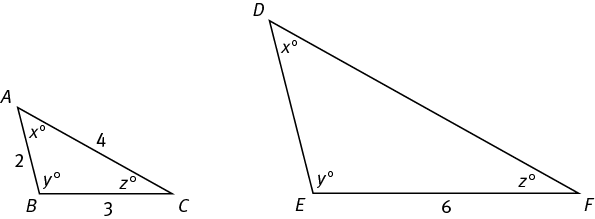
What is the perimeter of ∆DEF above?
Each triangle has an x° angle, a y° angle, and a z° angle; therefore, the triangles are similar, and corresponding sides are proportional to one another. BC and EF are corresponding sides; each is opposite the x° angle. Since EF is twice the length of BC, each side of ∆DEF will be twice the length of the corresponding side of ∆ABC. Therefore, DE = 2(AB) or 4, and DF = 2(AC) or 8. The perimeter of ∆DEF is 4 + 6 + 8 = 18.
The ratio of the areas of two similar triangles is the square of the ratio of corresponding lengths. For instance, in the example above, since each side of ∆DEF is 2 times the length of the corresponding side of ∆ABC, ∆DEF must have 22 or 4 times the area of ∆ABC.
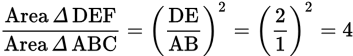
A right triangle has one interior angle of 90°, which is also the largest angle of the triangle. The longest side, which lies opposite the right angle, is called the hypotenuse. The other two sides are called the legs.
Pythagorean Theorem: The Pythagorean theorem holds for all right triangles and states that the square of the hypotenuse is equal to the sum of the squares of the legs.
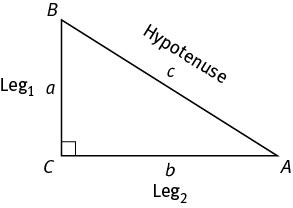
(Leg1)2 + (Leg2)2 = (Hypotenuse)2
or
a2 + b2 = c2
Some sets of integers happen to satisfy the Pythagorean theorem. These sets of integers are commonly referred to as “Pythagorean triples.” One very common set that you might remember is 3, 4, and 5. Since 32 + 42 = 52, you can have a right triangle with legs of lengths 3 and 4 and hypotenuse of length 5. This is the most common kind of right triangle on the GMAT. You should be familiar with the numbers so that whenever you see a right triangle with legs of 3 and 4, you will immediately know the hypotenuse must have length 5. In addition, any multiple of these lengths makes a Pythagorean triple; for instance, 62 + 82 = 102, so 6, 8, and 10 also make a right triangle. One other triple that appears regularly on the GMAT is 5, 12, and 13.
Don’t overuse the Pythagorean theorem. Easily recognizable right triangle patterns such as the triples allow you to avoid spending time on the formula when solving the majority of GMAT geometry problems. But from time to time the GMAT may challenge you with a triangle that doesn’t offer any convenient shortcuts, so make sure you can apply the Pythagorean theorem when necessary.
Example: What is the length of the hypotenuse of a right triangle with legs of length 9 and 10?
Use the Pythagorean theorem: the square of the length of the hypotenuse equals the sum of the squares of the lengths of the legs. Here the legs are 9 and 10, so you have
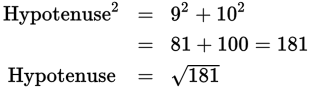
Special Right Triangles: You can always use the Pythagorean theorem to find the lengths of the sides in a right triangle. There are two special kinds of right triangles, though, that always have side lengths in the same ratios:
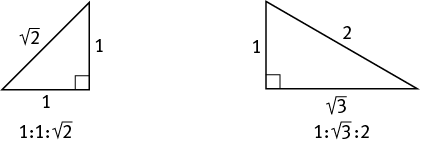
(for isosceles right triangles) (for 30-60-90 triangles)
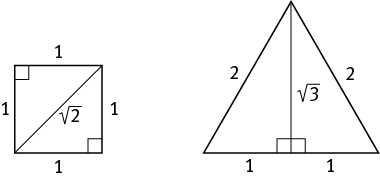
These two special right triangles appear frequently, and you are very likely to see them. However, the GMAT can hide them in unexpected ways. For example, the diagonal of a square creates two isosceles right triangles, also known as 45-45-90 triangles. And bisecting an equilateral triangle creates two 30-60-90 triangles:
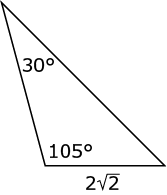
Now let’s use the Kaplan Method on a Problem Solving question dealing with triangles:
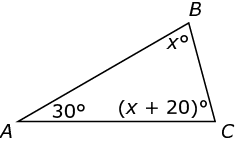
This is a straightforward triangle question that tests your knowledge of basic triangle properties. As with most questions in the Quantitative section, you can solve this one by using more than one approach. You could use algebra to solve for x, or you could backsolve, plugging the answer choices for x into the figure. With either method, you’ll need to remember the fact that the angles of a triangle sum to 180°.
Your task is to solve for x. You could use either algebra or backsolving.
If you solved with algebra, you’d use the fact that all the angles of a triangle sum to 180 degrees to set up this equation:
(D) is the correct answer.
If you backsolved, you could start with any answer choice, but as an example, let’s say that you started with (B). If you test x = 45, then the three angles of the triangle would be 30°, 45°, and 65°, which sum to 140°. You know triangles have 180°, so this answer choice is too small, and you can eliminate (A) and (B). Testing (D) yields angles of 30°, 65°, and 85°. These angles sum to 180°, which proves that (D) is correct.
Read back over the problem to confirm that your solution accurately follows from the information in the question. You were asked to solve for x. You’ve done so correctly, so you can move on to the next problem.
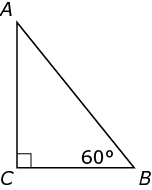
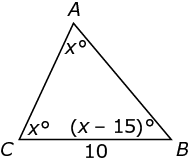
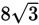, what is the length of AB?
