A polygon is a closed figure whose sides are straight line segments.
The perimeter of a polygon is the distance around the polygon, or the sum of the lengths of the sides.
A vertex of a polygon is the point where two adjacent sides meet.
A diagonal of a polygon is a line segment connecting two nonadjacent vertices.
A regular polygon has sides of equal length and interior angles of equal measure.
The number of sides determines the specific name of the polygon. A triangle has three sides, a quadrilateral has four sides, a pentagon has five sides, and a hexagon has six sides. Triangles and quadrilaterals are by far the most important polygons on the GMAT.
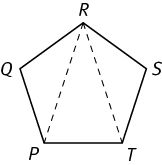
A polygon can be divided into triangles by drawing diagonals from a given vertex to all other nonadjacent vertices. For instance, the pentagon below can be divided into three triangles. Since the sum of the interior angles of each triangle is 180°, the sum of the interior angles of a pentagon is 3 × 180° = 540°.
Example:
What is the measure of one interior angle of the regular hexagon above?
You need to find the sum of the interior angles and divide by the number of interior
angles, or 6. Since the hexagon is regular, all angles are equal, so each of them
is equal to one-sixth of the sum. Since you can draw four triangles in a six-sided
figure, the sum of the interior angles will be 4 × 180°, or 720°. Therefore, each
of the six interior angles measures
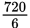or 120 degrees.
While splitting up polygons into triangles always works to find the sum of the interior
angles, there is a formula you can memorize to speed up the process. The sum of the
interior angle measures of a polygon with n sides is equal to (n − 2)180°. Therefore, in a regular polygon, the measure of each interior angle can
be calculated using this formula:
.
The most important quadrilaterals to know for the GMAT are the rectangle and square. Anything could show up on the test, but concentrate on the most important figures and principles. The lesser-known properties can readily be deduced from the way the figure looks and from your knowledge of geometry.
A quadrilateral is a four-sided polygon. The sum of its four interior angles is 360°.
A rectangle is a quadrilateral with four equal angles, each a right angle.
The opposite sides of a rectangle are equal in length. Also, the diagonals of a rectangle have equal length and bisect each other.
A square is a rectangle with four equal sides.
To find the area of a rectangle, you multiply the lengths of any two adjacent sides, called the length and width.
Area of a rectangle = length × width = lw.
To find the area of a square, since length and width are equal, you say:
Area of a square = (side)2 = s2.
In the rare event that you have to find the area of a parallelogram (a quadrilateral with equal and parallel opposite sides), multiply the base and the height.
Area of a parallelogram = base × height = bh.
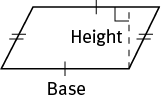
The diagonals of a parallelogram do not necessarily have equal length, but they do bisect each other.
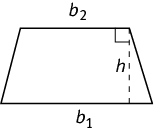
The area of a trapezoid—a quadrilateral with exactly one pair of parallel sides—can be calculated as follows:
Area of a trapezoid =
(the sum of the bases)(height) =
(b1 + b2)(h).
Now let’s use the Kaplan Method on a Problem Solving question dealing with polygons:
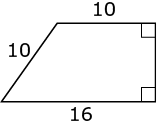
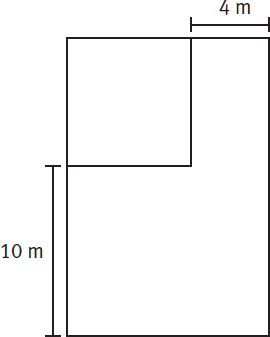
If this were a simple square or triangle, your work would be quick. However, when given an unfamiliar shape on the GMAT, you can often split the figure into smaller, familiar shapes to calculate the needed sides or angles.
The task is to solve for the perimeter of the figure, or the sum of the length of its sides. To do this, you need to determine the length of the unlabeled side.
Pattern Recognition helps you recognize that this polygon can be broken down into smaller, more manageable figures. In this case, you can break the shape into a rectangle and a right triangle. Drop a perpendicular from the left endpoint of the top horizontal side of length 10 to the bottom horizontal side of length 16.
This perpendicular will divide the quadrilateral into a right triangle and a rectangle. Because the lengths of the opposite sides of a rectangle are equal, the horizontal sides of the rectangle both have a length of 10. This means that the horizontal leg of the right triangle will have a length of 16 − 10, or 6.
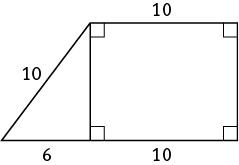
At this point you might recognize that the right triangle is a special right triangle. It is a 3:4:5 right triangle, and each side of it is a member of the 3 to 4 to 5 ratio multiplied by 2. The leg of length 6 is 2 × 3, and the hypotenuse of length 10 is 2 × 5. So the length of the other leg is 2 × 4 = 8. Because opposite sides of a rectangle are equal, the vertical side of the rectangle at the right also has a length of 8.
Now you can find the perimeter of the quadrilateral. The sum of the length of the figure’s sides is 16 + 10 + 10 + 8 = 44. That’s choice (B).
If you were short on time for this question, you could use Critical Thinking to strategically eliminate a few of the answer choices. In any right triangle, the hypotenuse is always the longest side of the triangle. So in the figure, the side shared by the triangle and rectangle must be less than 10, since it makes up one of the legs of the right triangle.
If the short side of the rectangle were equal to 10, then the perimeter of the total quadrilateral would be 10 + 10 + 10 + 16 = 46. Since you know that one of the sides must be less than 10, the perimeter must be less than 46. This definitively eliminates (C), (D), and (E), and you have a much better chance of picking the correct answer.
Read back over the problem, confirming that your solution accurately follows the information in the question.
