Coordinate Geometry

Slope

The slope of a line on a coordinate plane tells you how steeply that line goes up or down. If a line gets higher as you move to the right, it has a positive slope. If it goes down as you move to the right, it has a negative slope. To find the slope of a line, use the following formula:

Rise means the difference between the y-coordinate values of the two points on the line, and run means the difference between the x-coordinate values.

Example: What is the slope of the line that contains the points (1,2) and (4,−5)?

To determine the slope of a line from an equation, put the equation into slope-intercept form: y = mx + b, where the slope is m.

Example: What is the slope of the line given by the equation 3x + 2y = 4?

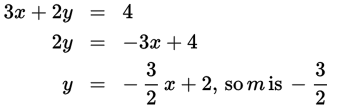
The word intercept in “slope-intercept form” is there because b is the value of the y-intercept—the point at which the line crosses the y-axis. Another way to think of that is that (0,b) will be a point on the line.

Perpendicular lines have slopes that are negative reciprocals of one another. For the line in this example, with a slope of , a perpendicular line would have a slope of .

Calculating Distance on the Coordinate Plane

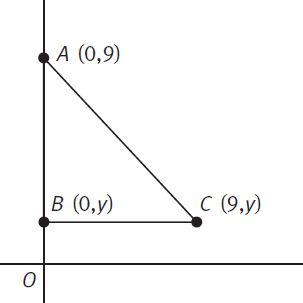
To determine the distance between any two points on a coordinate plane, you can use the Pythagorean theorem.

Example: What is the length of AB?

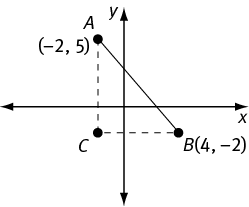
Right triangle ABC, where C measures 90 degrees.  Point A is located at the coordinate point (-2, 5) and point B is located at (4, -2).

Sketch lines from points A and B parallel to the axes. They will form a right triangle, and the intersection will have the same x-coordinate as one point and the same y-coordinate as the other. Because the new lines aren’t diagonal, their length is easy to figure out. In this example, the length of AC is 7 because the line drops down 5 from A to the x-axis and then another 2 to C. Similarly, the length of BC is 6.

Now you can use the Pythagorean theorem to calculate AB:

In-Format Question: Coordinate Geometry on the GMAT

Now let’s use the Kaplan Method on a Data Sufficiency question dealing with coordinate geometry:

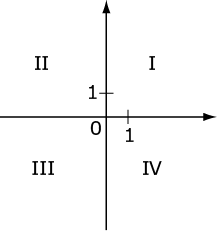
  1. A standard coordinate plane with quadrants I, II, III, and IV labeled, counterclockwise, beginning with the upper right quadrant.
    If st > 0, in which quadrant of the coordinate system above does the point (s,t) lie?
    1. (s,−t) lies in quadrant II.
    2. s is negative.

Step 1: Analyze the Question

In this Value question, you are asked to determine which quadrant the point (s, t) is in. You are told in the question stem that st > 0, which means that s and t are either both positive or both negative. This is only true in quadrants I and III.

Step 2: Evaluate the Statements Using 12TEN

Statement (1): You know that (s,−t) lies in quadrant II, which tells you that s is negative and −t is positive, so t must be negative. Because s and t are both negative, (s,t) is in quadrant III, and the statement is sufficient. Eliminate (B), (C), and (E).

Statement (2): You are told that s is negative, which is also sufficient, because you already deduced from the question stem that s and t have the same sign.

The correct answer is (D).

Practice Set: Coordinate Geometry on the GMAT

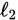  1. Line is given by the equation y = mx + 3, and line is given by the equation y = nx − 7; m and n are constants. Is 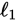parallel to ?

    1. m2 − n2 = 0
    2. mn is positive.
  2. A triangle is on the xy-coordinate plane, with vertex A at coordinates (0,9), vertex B at coordinates (0,y), and vertex C at coordinates (9,y).
    In the rectangular coordinate system above, triangle ABC has an area of 27 square units. Vertex A is at point (0,9), vertex B is at point (0,y), and vertex C is at point (9,y). What is the value of y?
    1. 1
    2. 2
    3. 3
    4. 4
    5. 6
  3. In the xy-coordinate system, if (m,n) and (m + 2, n + k) are two points on the line with the equation x = 2y + 5, then k =
    2. 1
    3. 2
    5. 4