-
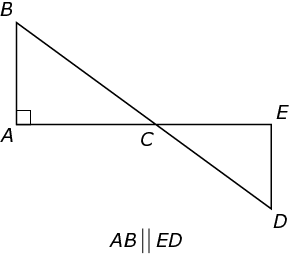
Note: Figure not drawn to scale.
In the figure above, ED = 1, CD = 2, and AE =  . What is the perimeter of ΔABC?
. What is the perimeter of ΔABC?
-
The diagram contains two triangles. More importantly, note that since the triangles meet at a common point, the angles that meet at that point (in this case, angles BCA and DCE) must be equal as well.
You’re given that sides AB and ED are parallel. This defines a relationship between angles ABC and CDE: they are equal. You’ll see this mentioned later in this chapter, but these two are alternate interior angles, formed by a line (called a transversal) that intersects two parallel lines.
Since angle BAC is a right angle, triangle ABC is a right triangle. And given that BA and ED are parallel and two pairs of angles are equal in the two triangles, then the measure of angle BAC must also be equal to that of CED, and both must equal 90 degrees. Triangles ABC and CDE are therefore similar triangles—their three angles have the same measures, and their side lengths share the same ratio.
Because right triangles have so many patterns that the test makers can write questions about, they are the most frequently tested geometric shapes on the GMAT. You’ll learn later in this chapter about the relationships certain right triangles display between their side lengths and angle measurements.
Pattern Recognition will play a key role here, as we’ll look at how the lengths of a right triangle can often give us more information about a triangle, such as angle measurements. Additionally, even though in this case you’re not translating a word problem into an equation, your ability to apply the Core Competency of Paraphrasing is important, since you can use information about one part of the figure to draw inferences about other parts. In particular, knowing how to interpret the information about the parallel lines will be the key to answering this question efficiently.
Here are the main topics we’ll cover in this chapter:
Now let’s apply the Kaplan Method to the geometry question you saw earlier:

 . What is the perimeter of ΔABC?
. What is the perimeter of ΔABC?
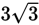

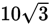
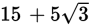

You’re given two triangles that meet at a certain point and are told that two of the line segments that form their sides are parallel. Additionally, you’re given that angle BAC is a right angle, which makes triangle ABC a right triangle. Since AB and ED are parallel, angles ABC and CDE are equal, because they are alternate interior angles formed by two parallel lines cut by a transversal. Angles BCA and DCE are also equal, since these are vertical angles. And since the measure of all interior angles of a triangle must add up to a specific number, 180, then angles BAC and CED must also be equal.
You’re asked to find the perimeter of triangle ABC. You’ll need to use the information about triangle CDE to be able to figure out the side lengths of ABC. The last step will be to add up the side lengths.
Since you know that CDE is a right triangle, you can use the Pythagorean theorem to first find the length of the missing side of triangle CDE by substituting the relevant values into the equation (ED)2 + (CE)2 = (CD)2.
However, if you noticed that one side of the triangle, ED, is equal to 1 and the hypotenuse, CD, is equal to 2, then you may recognize that this is a special right triangle, specifically
the 30-60-90 triangle. Recognizing this pattern will save you much time. If the hypotenuse
is twice the length of one of the sides of the triangle, then the side lengths of
the triangle will be in the ratio of
 . Therefore, side CE must have a length of
. Therefore, side CE must have a length of
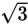 . Since you are given that AE equals
. Since you are given that AE equals
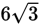 , leg AC must equal
, leg AC must equal
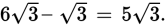
Since you established that the side lengths of triangle CDE are in the ratio of
 , and you identified that its corresponding angles are equal to those of triangle
ABC, then the two triangles are similar, and the three sides AB:AC:BC must also follow the ratio of
, and you identified that its corresponding angles are equal to those of triangle
ABC, then the two triangles are similar, and the three sides AB:AC:BC must also follow the ratio of
 . Because AC equals
. Because AC equals
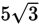 , AB must equal 5, and BC must equal 10. Therefore, the perimeter of triangle ABC is
, AB must equal 5, and BC must equal 10. Therefore, the perimeter of triangle ABC is
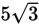 + 5 + 10, or
+ 5 + 10, or
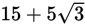 . Choice (D) is correct.
. Choice (D) is correct.
Make sure you’ve paired up the angles and their corresponding side lengths correctly, using the ratio of side lengths of a 30-60-90 degree triangle.
Now let’s look at each of the seven areas of geometry that show up on the GMAT Quantitative section, starting with lines and angles.